精密磨床液体静压轴承的多物理场耦合热分析*

郭传社，崔　怡

(上海理工大学 机械工程学院，上海　200093)



精密磨床液体静压轴承的多物理场耦合热分析*

郭传社，崔怡

(上海理工大学 机械工程学院，上海200093)

摘要：为了提高精密磨床的加工精度，以机床主轴系统的液体静压轴承为研究对象。通过应用热流固耦合(Thermal Fluid Solid Interaction, TFSI)方法求解该耦合系统的连续性方程、能量方程和Navier-Stokes方程组，得到耦合系统的油膜压力场、油膜温度场、轴承温度场、轴承变形场等参数。结果表明，随着轴颈转速的增加，滑动轴承油膜压力和温度不断增加；随着供油压力的增加，油膜温度几乎没有变化。文章得出的仿真结果对液体静压轴承的结构设计和工艺参数优化有一定的参考意义,且采用有限元软件计算液体静压轴承耦合传热问题能更有效地反映真实的传热情况。

关键词：精密机床；液体静压轴承；多物理场耦合

0引言

液体静压轴承具有回转精度高、摩擦系数小、使用寿命长、适应性好和抗振性能强等优点，在精密加工机床中得到广泛的应用[1]。液体静压轴承的油膜温度对轴承精度有着重要影响，会使轴承发热并产生热变形，影响轴承结构变形，从而降低机床性能和主轴精度，对精密机床的加工精度极为不利，必须合理控制。轴承系统中轴瓦、润滑油、轴承衬套之间的传热是相互影响、相互制约的[2-4]。传统方法是采用雷诺方程[5]或单纯的计算流体动力学CFD法[6-7]求解轴承油膜特性，而忽略了轴承系统液体与固体之间的耦合作用。很多学者对轴承系统进行了研究[8-10]，郭力等对动静压轴承温度场和热变形进行了仿真分析，得出了动静压轴承的温度分布情况[11]。Zhang等建立了润滑油的粘温方程和静压轴承油膜温升的数学模型并采用有限体积法模拟了变油膜厚度下油膜的温度场，揭示了油膜厚度对轴承温升的影响规律[12]。夏毅敏等研究了非球面超精密加工机床液体静压推力轴承的温度场分布，得出随着油膜厚度降低，温度升高[13]。林起崟等对高速滑动轴承流固耦合传热及流场分析作了研究，解决轴瓦、润滑油和轴颈之间流固界面的温度和换热系数等传热边界条件难以确定的问题[14]。但是这些研究通常只考虑了一些物理量对轴承系统的影响，而未考虑同时把这些物理量耦合。根据经典连续方程和雷诺方程对流体域进行描述，弹性力学方程对固体域进行描述，采用热流固耦合(TFSI)方法对毛细管节流四腔轴承润滑系统进行多场耦合热分析，从而得到轴承的温度场和变形场。

1热流固耦合分析计算模型

1.1流体域控制方程

液体静压轴承中润滑油的流动情况可以用以下控制方法来描述：

(1)质量守恒方程

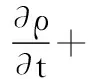
(1)

式中，ρ为密度；v为速度矢量。

(2)动量守恒方程

(2)

式中，τ为应力张量，形式如下：

(3)

(3)能量守恒方程

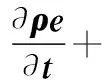
(4)

式中，f是体积矢量；▽是拉氏算子；q是热流密度。

1.2雷诺方程

雷诺方程是Navier-Stokes方程在流体动力润滑中具体应用的一种特殊形式。假定流体为牛顿流体，其油膜接触面无滑移。将雷诺方程与边界条件耦合后，得到方程:

(5)

式中：h为油膜厚度；p为油腔压力；V为油腔体积；v1,v2分别为油膜两侧速度。

1.3固体热传导方程

固体热传导方程为：

(6)

2静压轴承结构及耦合模型

2.1静压轴承结构

液体静压轴承依靠外部供油系统向轴承供给润滑油，通过补偿元件输送到轴承的油腔中，形成具有足够压力的润滑油膜将轴颈浮起。液体的静压力支撑主轴，在一定的载荷范围内，可以保证主轴在任何转速或静止时都与轴承处于完全液体摩擦状态，不会形成干摩擦，有利于保证主轴旋转精度。常用的恒压或恒流供油静压轴承系统主要包括向心或推力轴承、补偿元件(如小孔节流、毛细管节流、反馈式节流、定量泵等)、供油装置(油泵、电机、油箱等)。静压轴承及供油系统如图1所示。图2所示为根据流场力学计算特点简化的四腔静压轴承模型。

图1　静压轴承与供油系统

图2　四腔轴承的结构简图

2.2耦合模型的建立

超精密加工机床的液体静压轴承的节流器均为毛细管节流。该静压轴承共有4个油腔。取轴承半径R=45mm，轴承宽度B=105mm，轴向封油边宽度C1=8mm，静压腔包角2θ=70°，油腔长度L=84mm，周向封油边宽度b1=(45-θ)πR/180，毛细管节流最佳节流比β=2，轴承半径间隙h0，2h0=30μm，进油口直径5mm，建立其轴承和油膜结构如图3和图4所示。

图3　轴承三维模型

图4　油膜示意图

由于轴承几何形状简单，直接在ANSYS CFX的前处理中建立模型，并对其进行网格划分。为了提高计算的准确性，对于厚度极薄的油膜，采用六面体网格进行划分。此外，为了提高计算准确性的同时减小计算量，可将油膜与油腔切割，进行分块网格划分。油膜处的网格尺寸设置较小，油腔处的网格尺寸相比偏大。耦合系统有限元网格模型如图5所示。

图5　耦合系统有限元网格模型

计算模型的基本假设为：①润滑油为不可压缩牛顿流体；②不考虑液体重力，进行稳态分析；③油膜外表面与轴承衬套为耦合界面，其相对速度为0。

边界条件的设定为：①设定进口压力为1.5MPa，初始温度为20℃；②油膜轴向出油口压力为0MPa；③轴承油膜与主轴重合的壁面设为旋转壁面，转速为2000r/min，无滑移。边界条件设定完毕后，设定High Resolution高阶混合差分格式的计算精度，收敛容差数量级为1×10-4，最后设置迭代步数及求解控制方程。

3数值模拟计算

轴承油膜的流动满足流体力学的基本方程，静压轴承的流场计算可应用流体力学的方法。ANSYS CFX软件采用全隐式多网格耦合求解，能同时求解动量方程和连续性方程，且稳健快速。

3.1油膜及轴承材料参数的选定

本文中选用的轴承润滑油为L-FD10，轴瓦承材料选用低碳钢，轴承衬套材料选用巴氏合金，其具体性能参数见表1。

表1　材料参数

3.2油膜压力分析

当进油压力为1.5MPa，转速2000r/min时的油膜压力分布如图6所示，沿轴向从油腔到封油面再到轴承边缘，油膜压力逐渐减小。如图7所示，在相同供油压力条件下，随着轴颈转速的提高，油膜压力相应增加，但同时也增大了油膜发生破裂的概率。在轴颈转速不变的条件下，随着供油压力降低，润滑油膜发生破裂的概率增大，破裂发生后，随着供油压力的降低，破裂区域增大。

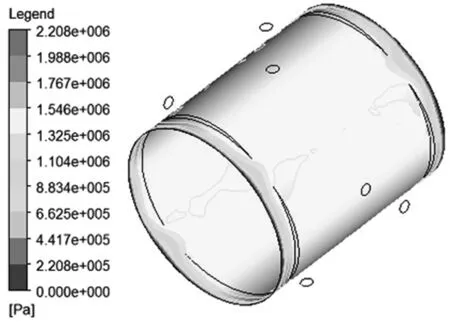
图6　油膜压力分布

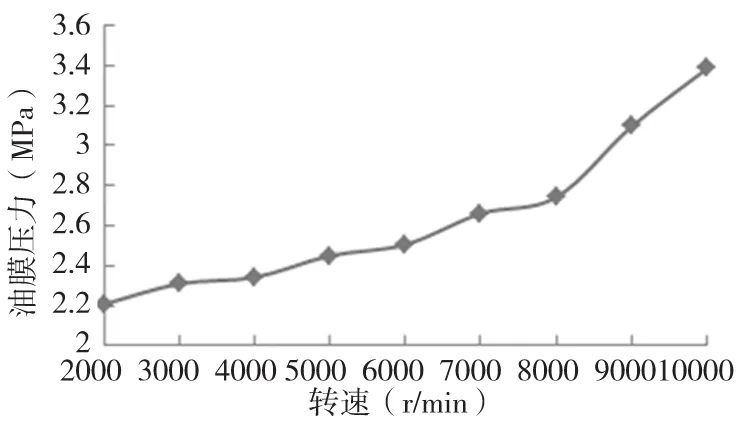
图7　相同供油压力，转速与油膜最高压力的关系

3.3温度分析

经计算，得到了不同参数下的液体静压轴承及内部流体温度场的分布云图和分布规律，当转速2000r/min，油膜厚度30μm时，不同进油压力对油膜温升的影响如图8所示。从图中可以看出，当入口压力为1.5～6MPa时，温度的变化受入口压力影响很小，可以忽略不计，同时这说明要想通过改变入口压力来降低油膜的温升是行不通的，应该另辟蹊径。不同入口压力下所产生的云图趋势非常相似，从单个温度云图来看，由于油腔很深，油液摩擦剪力很小，油腔油液温升很小，而封油面油膜厚度很小，油液摩擦剪力很大，产生大量的摩擦热，是产生温升的主要区域。

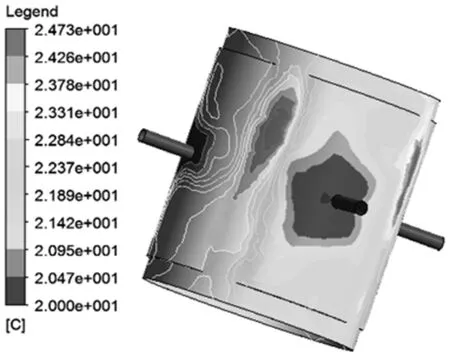
(a)p=1.5MPa

(b)p=3MPa

(c)p=4.5MPa

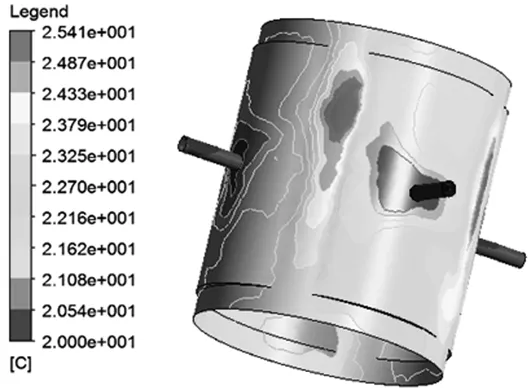
(d)p=6MPa

图9为油膜温度受转速的影响。由图9可以看出，在其它参数相同的情况下，轴承油膜温升随着轴颈转速的提高而增大。可见，轴承转速对油膜温升的影响较大，当温升较大时，轴承的承载力和油膜刚度也会因润滑油的粘度不均匀产生影响，导致轴承回转精度下降等。

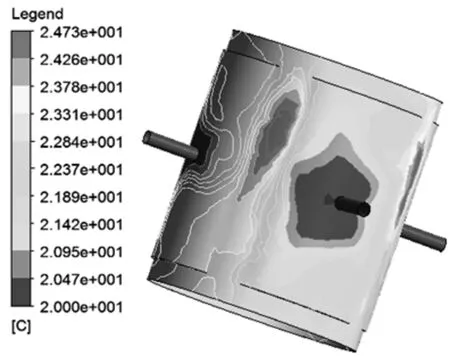
(a)n=2000r/min

(b)n=4000r/min

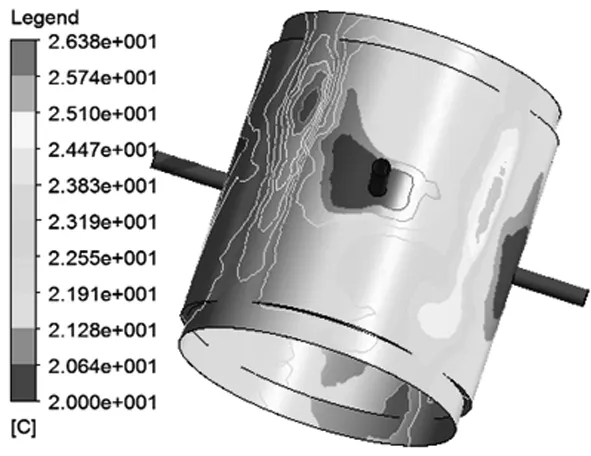
(c)n=6000r/min

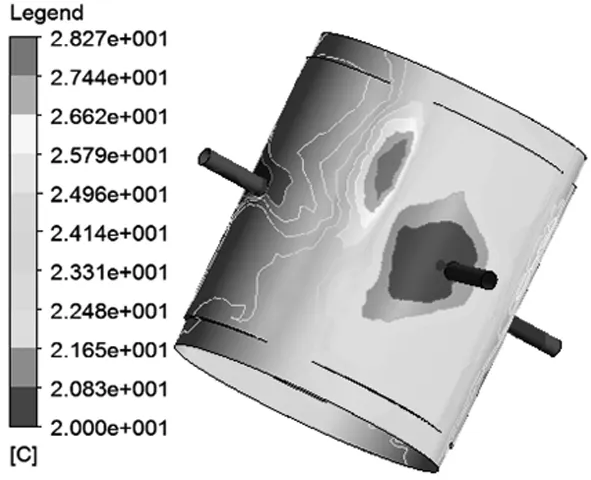
(d)n=8000r/min

把CFX中计算的油膜温度结果作为载荷施加给轴承，设置轴承材料，得到轴承的温升变化，如图10所示。通过温度分布图可以有针对性地改善轴承的散热，这不仅降低了通过多次实验所带来的高额成本，同时也给为实验提供了重要的理论依据。

图10　轴承温度场

3.4变形分析

以温度为载荷施加给结构场，给轴承法兰面施加约束，计算得到轴承的变形场，如图11所示。当转速2000r/min，油膜厚度30μm，入口压力3MPa时，轴承的最大变形为1.41μm。

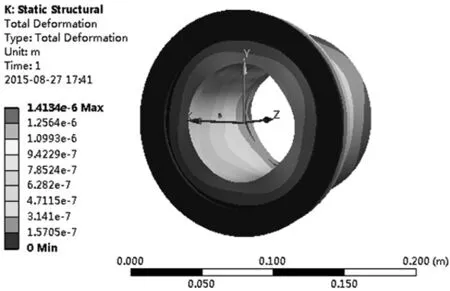
图11　轴承变形场

4结论

根据液体静压轴承的特点，分析了轴承结构特点及热流固耦合的理论模型。通过热流固耦合(TFSI)方法，采用ANSYS软件的三个模块(Fluid Flow、Steady-State Thermal及Static Structural)对主轴转速与轴承油膜最高压力的关系、不同进油压力和不同转速对油膜温度的影响以及轴承的结构变形做了研究。得出如下结论：

(1)采用流体动力学方法，应用Fluid Flow(CFX)软件可以准确地模拟流场和温度场，但划分计算网格的数目应当适中，以即能保证分析精度，又不会花费太多计算时间为宜。

(2)利用TFSI(流体、固体、热三场耦合)方法，对液体静压轴承进行分析。直观反映油膜压力、温度及轴承温度、变形分布。

(3)在供油压力等其它参数不变的情况下，滑动轴承油膜压力和温度随着轴颈转速的增大而不断增加；在转速等其它参数不变的情况下，随着供油压力的增加，油膜温度几乎没有变化，完全可忽略不计，想通过改变入口压力改变润滑油的温度与粘度是不现实的。

[参考文献]

[1] 秦大同, 谢里阳. 轴承[M]. 北京：化学工业出版社, 2013.

[2] 刘晓卫，王 崴，王庆力．基于ANSYS的高速角接触球轴承温度场分析[J]．组合机床与自动化加工技术，2015(3):13-20.

[3] 崔海龙，岳晓斌，张连新,等.基于ANSYS的多孔质静压轴承径向特性数值模拟[J]. 组合机床与自动化加工技术,2014(11):43-45.

[4] 张杰，郭宏升.水润滑动高速动静压滑动轴承数值模拟[J].农业机械学报，2008,39(6):159-162.

[5] Bouyer J，Fillon M.On the significance of thermal and deformation effects on a plain journal bearing subjected to severe operating conditions[J].Journal ofTribology,2004,126(4):819-822.

[6] Gertzos K, Nikolakopoulos P, Papadopoulos C. CFD analysis of journal bearing hydrodynamic lubrication by bingham lubricant[J]. Tribology International,2008,41(12):1190-1204.

[7] Hartinger M,Dumont M L,Loannides S,et al.CFD modeling of a thermal and shear-thinning elasto-hydrodynamic line contact[J].Journal of Tribology,2008,130(4):1-16.

[8] Shenoy S B, Pai R, Rao D, et al. Elasto-hydrodynamic lubrication analysis of full journal bearing using CFD and FSI techniques[J].World Journal of Modelling and Simulation, 2009,5(4):315-320.

[9] Liu H, Xu H, Ellision P J, et al. Application of computational fluid dynamics and fluid-structure interaction method to the lubrication study of a rotor-bearing system[J]. Tribology Letters,2010,38(3):325-336.

[10] Li Q,Liu S,Pan X,et al.A new method for studying the 3D transient flow of misaligned journal bearings in flexible rotor-bearing systems[J].Journal of Zhejiang University-Science A,2012,13(4):293-310.

[11] 郭力，李波，章泽．液体动静压轴承的温度场与热变形仿真分析[J]．机械科学与技术，2014(4):49-53．

[12] Zhang YQ,XuXQ,YangXD,et al.Analysis on Influence of Oil Film Thickness on Temperature Field of Heavy Hydrostatic Bearing in Variable Viscosity Condition[C]//2011 International Conference on Chemical Engineering and Advanced Materials, Changsha, 2010:1181-1185.

[13] 夏毅敏,张刚强,罗松保,等. 非球面超精密机床静压轴承温度场的分布[J].光学精密工程，2012,20(8):1759-1764.

[14] 林起崟，魏正英，唐一平，等. 高速滑动轴承流固耦合传热及流场分析[J]．润滑与密封，2010,35(10) :28-35．

(编辑李秀敏)

Coupled Thermal Analysis of Multi-physical Field of Hydrostatic Bearing in Precision Grinding Machine

GUO Chuan-she，CUI Yi

(School of Mechanical Engineering,University of Shanghai for Science & Technology,Shanghai 200093,China)

Abstract：In order to improve the machining accuracy of precision grinding machine, the hydrostatic bearing of machine tool spindle system as the research object. Through the thermo-hydro-mechanical three field coupling method (TFSI), the continuity equation, energy equation and Navier-Stokes equation of the coupled system can be solved, then parameters likes pressure field and temperature field of oil film, temperature field and deformation field of bearing and so on are obtained. The analysis results show that the oil film pressure and temperature of the sliding bearing are increasing with the increase of the shaft speed; With the increase of oil supply pressure, there are little changes of oil film temperature; The simulation results of this paper have some reference value for the structural design and process parameters optimization of the hydrostatic bearing, and the coupled heat transfer problem of liquid static pressure bearing is more effective to reflect the real heat transfer conditions by using the finite element software.

Key words：precision machine tool; hydrostatic bearing；multi-physical field coupling

文章编号：1001-2265(2016)05-0017-05

DOI:10.13462/j.cnki.mmtamt.2016.05.005

收稿日期：2015-08-29；修回日期：2015-09-25

*基金项目：国家科技重大专项( 2011ZX04004-051)

作者简介：郭传社(1987—)，男，山东菏泽人，上海理工大学硕士研究生，研究方向为机床热分析，(E-mail)gcs819@163.com。

中图分类号：TH133.3；TG506

文献标识码：A