周期性内波对横置圆柱体作用的试验研究❋

郭海燕， 吴凯锋， 王　飞, 马　东， 王新超

(中国海洋大学工程学院，山东 青岛 266100)

研究简报

周期性内波对横置圆柱体作用的试验研究❋

郭海燕， 吴凯锋， 王飞, 马东， 王新超

(中国海洋大学工程学院，山东 青岛 266100)

摘要：本文对分层流体中周期性内波与水下横向放置圆柱体模型的相互作用进行了试验研究。采用摇板法进行了内波造波试验，通过染色试验配合CCD系统得到周期性内波的相关波要素；利用测力系统对圆柱体模型在内波作用下的受力进行测量分析，得到了横置圆柱体模型上垂向力随周期性内波作用及水深的变化规律，同时对圆柱体模型垂向力和水平力进行了耦合分析。结果表明：圆柱体的垂向力会随着周期性内波的变化而变化，其最大值也会随着水深发生变化。密度跃层处横置圆柱体模型水平力的主要频率是垂向力主要频率的两倍，两个方向的内波作用力耦合后呈现“8”字形态。

关键词：内波； 横置圆柱体； 测力系统； 垂向力； 水平力

引用格式：郭海燕， 吴凯锋， 王飞, 等. 周期性内波对横置圆柱体作用的试验研究[J].中国海洋大学学报(自然科学版)，2016, 46(5)： 111-118.

GUO Hai-Yan， WU Kai-Feng， WANG Fei, et al. Experimental investigations on the interaction of periodic internal waves with a horizontal cylinder[J].Periodical of Ocean University of China, 2016, 46(5)： 111-118.

内波是发生在密度跃层海洋中，且最大振幅出现在其内部的波动。内波几乎贯穿整个海洋深度，但海洋表面通常不会有明显的表现。海洋内波的波长范围可达几百米至上百千米；在温跃层处，内波振幅可达百米量级，因此它会产生巨大的波浪力，可以使海洋结构物发生整体推移或扭转。因此，在内波活动频繁的海洋区域，海洋结构物和水下航行体等的设计必须考虑内波产生的作用力。近年来，随着“海洋强国”战略的提出，中国对油气资源十分丰富的南海的开发重视程度急剧增加，但南海海域海水运动复杂，海底地形多变，是内波的多发区域，所以研究内波对我国开发南海资源具有十分重要的意义。

近几年，关于内波及其与结构物相互作用研究国外报道较少，而国内相对较多[1-5]。Arntsen[6]进行了经典的在分层流体中拖曳水平圆柱体生成内波的试验，通过处理试验结果得到了圆柱体上内波引起的曳力系数和升力系数，并给出了这2个系数与内Froude数的关系。周喜武[7]、Xu Zhaoting等[8]在试验室中进行了水平运动Rankine卵形体生成内波的试验，得到了曳力系数与内Froude数的关系。蔡树群等[9]将海洋工程中常用于波浪力计算的Morison公式引入孤立子内波对圆柱形桩柱作用力的计算，采用模态分离法来计算，所得解的精度取决于观测资料的数量和所保留的模态数目，并且认为孤立子内波对桩柱的作用力和力矩远大于表面波。之后，程友良[10]和叶春生[11]相继采用Morison公式计算了内波作用于小直径圆柱体的作用力，得到了内波在两层流体之间产生的作用力方向相反的结论，并指出最大作用力和力矩与内波振幅相关。徐肇廷等[12]试验研究了水平桩柱与内波的相互作用，分析了水平阻力与内波波要素的关系。尤学一等[13]采用推板造波方法数值模拟了表面波与内波的相互作用场，并使用Morison公式计算了水平小尺度圆柱受到的内波和表面波联合作用力。谢皆烁等[14]分别采用MCC理论和KdV理论计算了两层流体中大振幅、强非线性内孤立波对小直径圆柱体的作用力和力矩，并对基于这2种理论的结果进行了比较分析。徐小辉等[15]试验研究了周期性内波对水下Suboff潜体的作用并得到内波波浪力随潜深及内波作用变化的规律。

由上可以看出关于内波与对结构物的作用力研究在数值模拟方面比较多，而且多是对单一方向力的研究，在试验方面的研究相对较少，对周期性内波经过时结构物在垂向与水平向2个方向力的耦合研究尚未见有报道。本文通过试验不仅分析了周期性内波经过时圆柱体垂向受力的一般规律，也对圆柱体水平力进行了分析，并且对2个方向的力进行了耦合分析。

1试验方法

试验是在中国海洋大学物理海洋试验室二维分层流及内波水槽中进行。试验设备主要由水槽及内波测量系统、圆柱模型和测力系统组成。

水槽长15m、宽0.35m、高0.7m，额定水深为0.6m。采用Oster双缸法制取密度分层水，上层为染色淡水，密度ρ1=0.999g/cm3，厚度为28.75cm；下层为透明盐水，密度ρ2=1.025g/cm3，厚度为28.75cm。水槽的一端装有摇板式内波造波机，通过控制摇板周期可改变内波周期，控制摇板幅度可改变内波振幅。本次试验中，设定的周期性内波的周期为8～14s，对应的频率为0.125～0.07143Hz。通过染色摄影技术配合CCD系统，可以得到需要的周期性内波的波速、振幅和波长等相关的波要素。相应的内波波要素见表1。

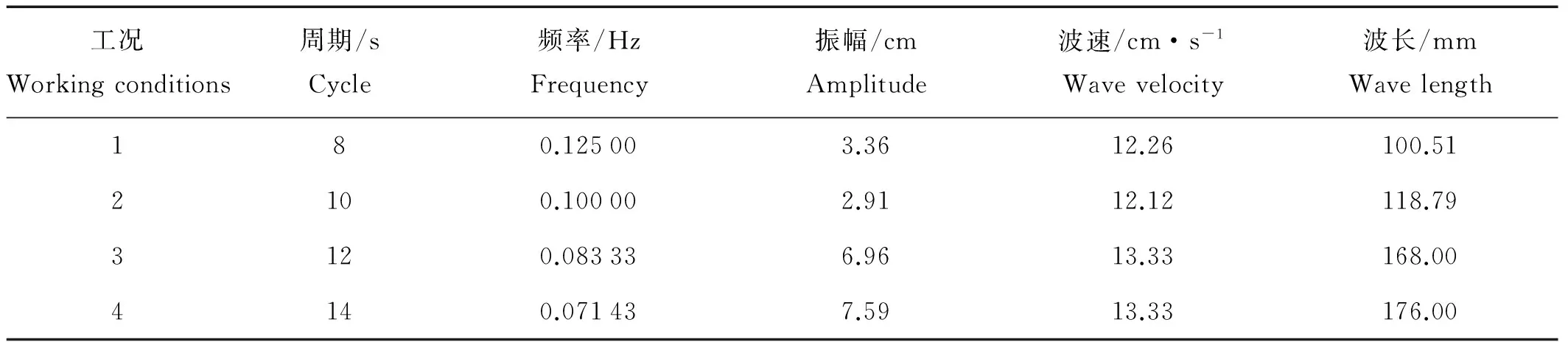
表1　内波波要素

试验采用pvc制作的圆柱体模型，模型长33cm、直径4cm。试验取A、B、C三个完全相同的模型，在水中的位置为：A模型顶面距水面21.5cm；B模型顶面距水面32.5cm；C模型顶面距水面28.5cm。

图1为模型实验示意图。为避免内波反射波对实验数据的影响，综合考虑水槽长度、波长、波速等因素，经过测算，A圆柱体安装在距离水槽左侧末端8m位置处。

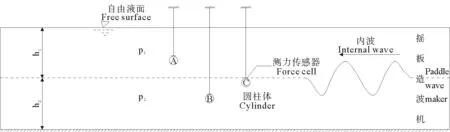
图1　模型试验示意图

圆柱体模型通过测力传感器与刚性杆件进行固定连接，其所受内波载荷由定制的测力传感器测量。本试验采用的测力传感器是L6J4型一维测力传感器和S2-001NHL型二维测力传感器，量程分别为50和100g，精度分别达到0.05%和0.1%，能够保证测量精度的要求。A、B圆柱体与一维传感器相连，用以测量垂向力；C圆柱体与二维传感器相连，用以测量垂向力和水平力。对传感器进行率定，利用率定公式可以将传感器采集到的电压信号关系直接转换成力值关系。

2试验数据处理及分析

实验过程中，本文用CCD对内波进行监测，分析过程中没有看到明显的表面波产生，故不考虑表面波对实验结果的影响。

由于试验环境的影响和系统误差的存在，试验进行过程中所采集的信号会有一些干扰成分，图2为采集到的作用力原始信号时程曲线，为了更清晰的反应作用力随时间变化，采用Butterworth低通滤波器对原始数据进行滤波处理，用Matlab进行程序编写，去除1 Hz以上的干扰信号后得到的时程曲线如图3，可以看出滤波后的结果能更好地反映周期性内波经过时横置圆柱体的垂向力随时间的变化情况。

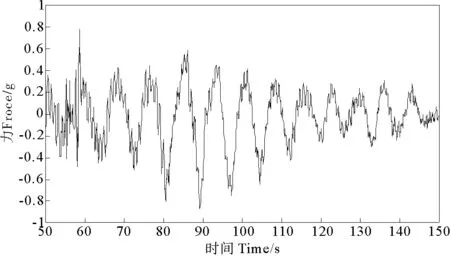
图2　原始图像

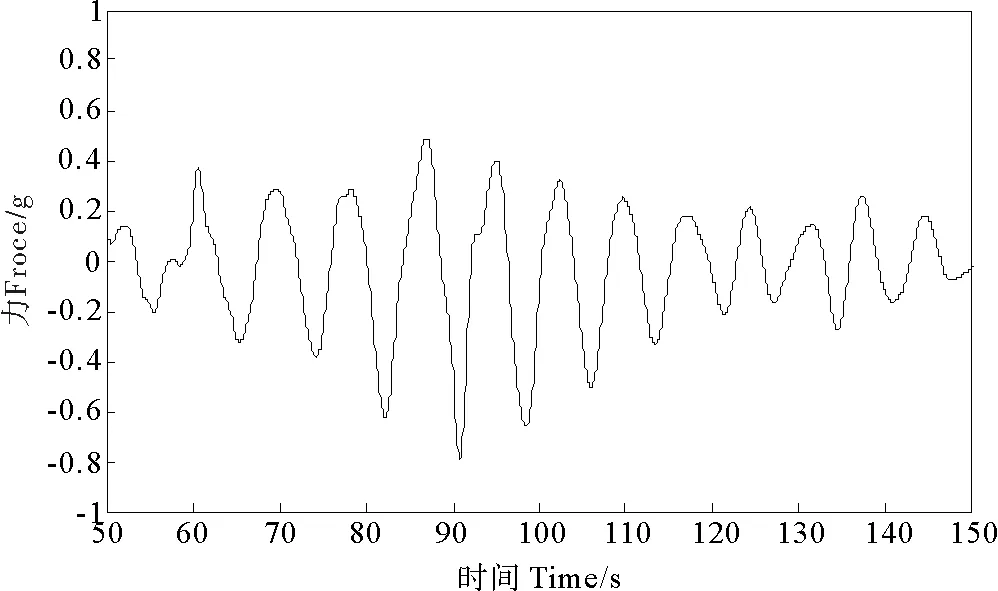
图3　滤波后图像

2.1 不同水深圆柱体垂向受力分析

通过试验得到了设计工况下横置圆柱体所受的垂向力时程曲线和频谱图。进行试验数据结果分析时，为了更好的分析内波经过时的情况，圆柱体的垂向力时程曲线只取内波经过时的时间段进行分析，见图4～7。

图4　内波周期为8 s的时各圆柱体垂向力时程曲线和频谱图

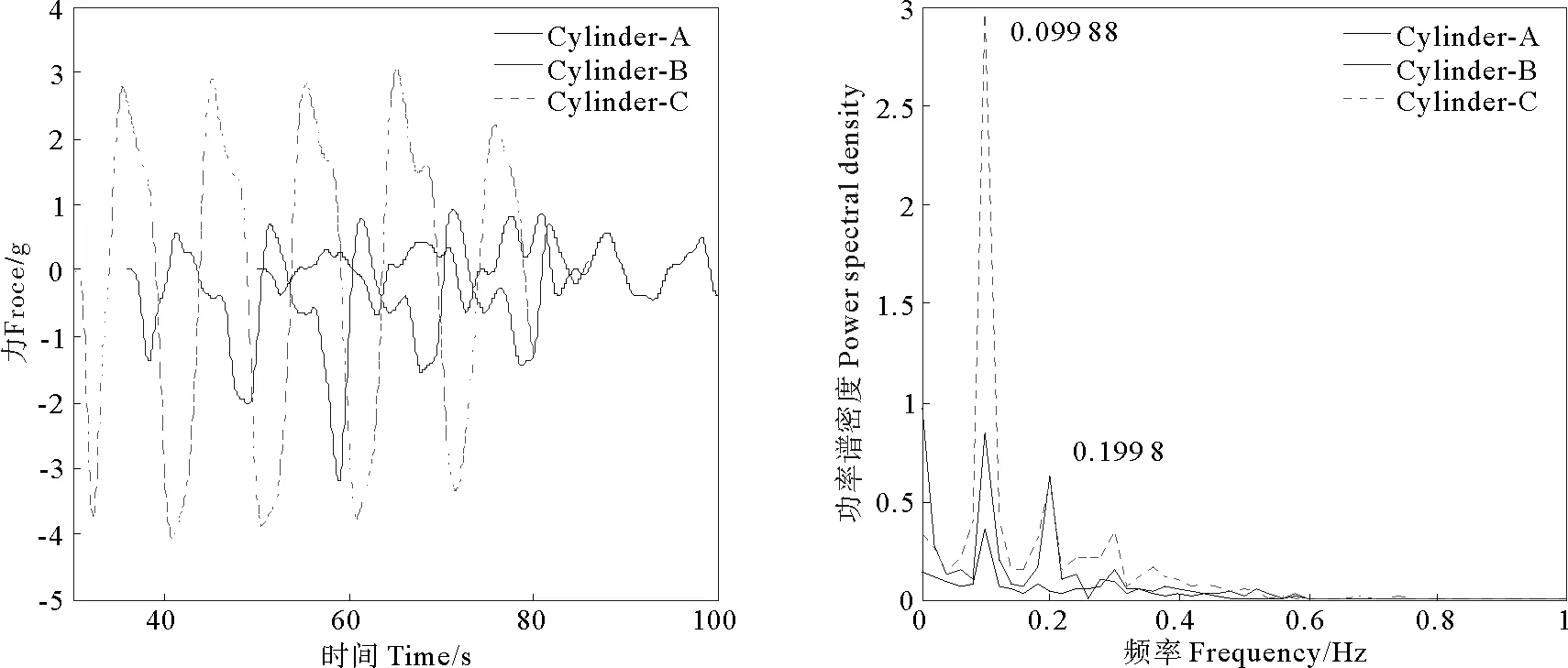
图5　内波周期为10 s的时各圆柱体垂向力时程曲线和频谱图

图6　 内波周期为12 s的时各圆柱体垂向力时程曲线和频谱图

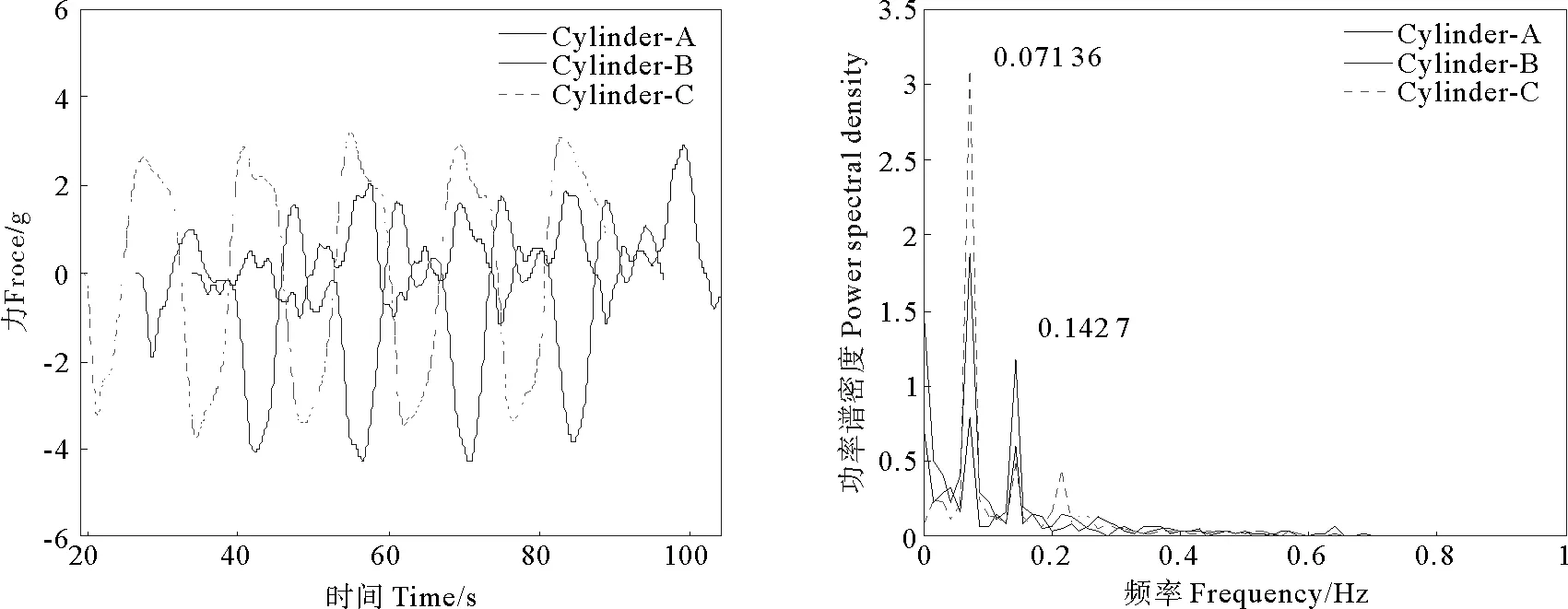
图7　内波周期为14 s的时各圆柱体垂向力时程曲线和频谱图

内波周期为8s时(见图4)，A、B、C 3个圆柱体模型所受的垂向力呈现周期性变化，变化的主要频率为0.1248Hz，与内波频率(0.125Hz)基本一致。此外，从频谱图中可以看出圆柱体所受垂向力的响应频率存在1个2倍于主要频率的成分。同样从图5、6、7中也可以看出，对应内波周期分别为10、12、14s时，3个圆柱体模型所受垂向力呈周期性变化，变化的主要频率与内波频率基本一致。从频谱图中可以看出圆柱体所受垂向力的响应频率存在1个2倍于主要频率的成分。

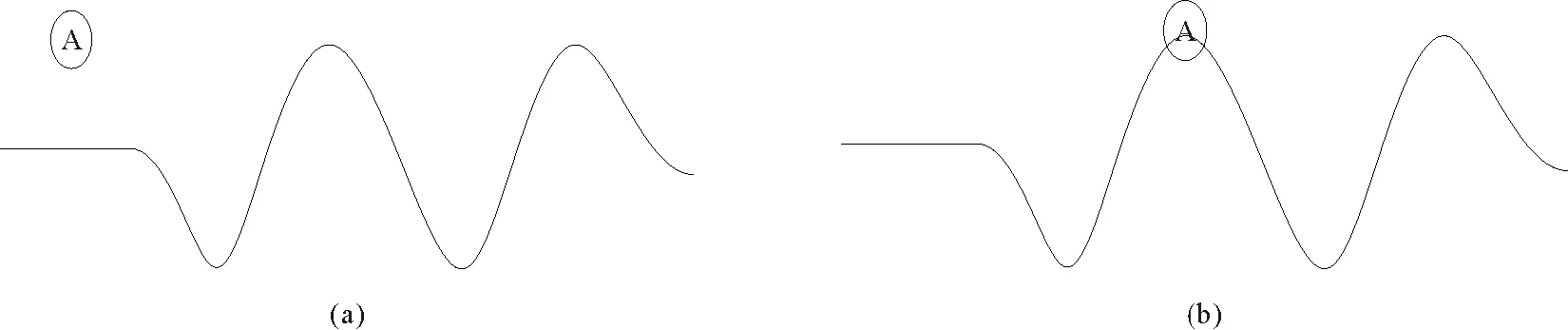
图8　A圆柱体与周期性内波相对位置示意图

从图4～7中可以看出，圆柱体A的垂向受力为正向时数值较大，负向时数值较小，表现出较强的非对称性；圆柱体B、C也有类似规律，表现为受力为正向时数值较小，负向时数值较大。经分析是由于圆柱体所受浮力变化所致，下面以圆柱体A为例进行分析。

图8为A圆柱体与周期性内波经过时的相对位置示意图。如图8(a)，在波峰经过之前，A圆柱体受到的垂向力只有内波作用的贡献，即F垂=F内。当内波波峰经过时，界面上移，A圆柱体有部分进入到下层流体中，如图8(b)。由于上下两层流体密度不同，A圆柱体受到的浮力会增大，记为ΔF浮，此时A圆柱体垂向力为F垂=F内+ΔF浮，这时A圆柱体垂向力正向有一个较大的增长，因此，A圆柱体垂向力时程曲线会表现出比较强的非对称性，内波力最大值应取负向力绝对值的最大值。对B和C圆柱体进行同样的分析可以得出：B和C圆柱体垂向力时程曲线同样表现出比较强的非对称性，内波力最大值都应该取正向力的最大值。

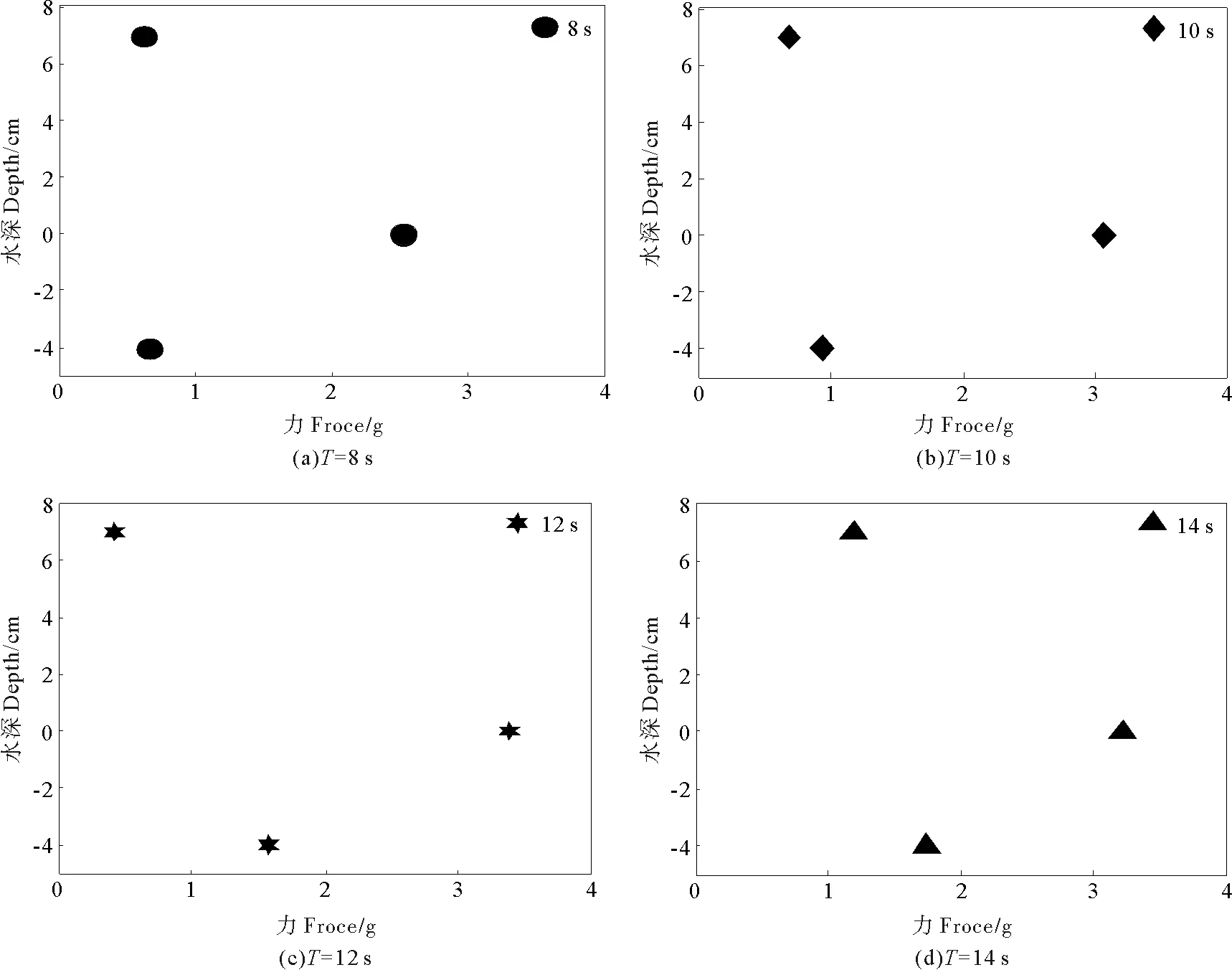
图9　垂向力最大值随水深变化

图9为内波周期分别为8、10、12和14s时，圆柱体处在水槽中上层流体、密度跃层和下层流体3个不同位置时所受垂向力最大值的变化图，图中内波垂向力的最大值按照上面的选取方法进行选取。以密度跃层处(C圆柱体所处位置)为纵坐标零点，正向为上层流体，负向为下层流体。从图9中可以看出在靠近密度跃层处，圆柱体受内波在垂向上的作用力比较大，离跃层较远时圆柱体受内波作用的垂向力比较小。

2.2 界面处圆柱体受垂向力与水平力的耦合分析

图10对应内波周期分别为8、10、12、14s时，C圆柱体模型受水平力的时程曲线和频谱图。对比图4～7中C圆柱体在相应周期内波作用下受垂向力的时程曲线和频谱图可以看出：周期性内波经过时，密度跃层处横置圆柱体垂向力的主要频率与内波频率基本一致，同时存在1个2倍于主要频率的成分；水平力的主要频率是内波频率的2倍，也存在一个与内波频率基本一致的频率成分。

对C圆柱体在受到不同周期内波作用下的垂向力与水平力进行耦合分析。内波周期为8、10、12、14s时，C圆柱体垂向力与水平力的耦合分析结果如图11(a)(b)(c)(d)。从图11(a)、(b)和(c)可以看出：圆柱体垂向力和水平力耦合，呈现“8”字形态，这是因为圆柱体水平力的主要频率是垂向力主要频率的两倍。圆柱体在垂向上受力没有出现零轴线对称，而是偏向于负方向，这是因为在内波经过时圆柱体垂向力会受到浮力变化的影响。图11(d)中圆柱体垂向受力同样没有关于零轴线对称，偏于负向，但其两个方向力的耦合比较杂乱无章，没有呈现明显的“8”字形。

图10　C圆柱体水平力时程曲线和频谱图

图11　垂向力与水平向力耦合图

3结论

本文采用摇板造波方式，在中国海洋大学物理海洋试验室二维分层流及内波水槽中试验研究了密度分层流体中周期性内波与横向放置的圆柱体相互作用的规律。通过对试验数据的综合分析，获得以下主要结论：

(1)周期性内波经过时，横向放置的圆柱体模型在垂向会受到周期性的作用力，且该作用力的主要频率与内波频率基本一致；圆柱体垂向力的频率中除了与内波频率基本一致的主要频率外，还存在1个2倍于主要频率的成分。

(2)在不同水深处，圆柱体在内波作用下的垂向力大小不同，在靠近密度跃层处圆柱体所受的垂向力比较大，离密度跃层较远时圆柱体的垂向力比较小。

(3)在密度跃层处，圆柱体受到的水平力的主要频率是两倍于内波频率的成分，也存在1个与内波频率基本一致的频率成分；圆柱体垂向力与水平力耦合后呈现出“8”字形。

参考文献：

[1]付东明, 尤云祥, 李巍.两层流体中内孤立波与潜体相互作用数值模拟[J]. 海洋工程, 2009, 27(3)： 38-44.

FU D M, YOU Y X, Li W.Numerical simulation of internal solitary waves with a submerged body in a two-layer fluid[J].The Ocean Engineering, 2009, 27(3)： 38-44.

[2]方欣华, 杜涛.海洋内波基础和中国海内波[M]. 青岛： 中国海洋大学出版社, 2005.

FANG X Hua, DU T.Fundamentals of Oceanic Internal Waves and Internal Waves in the China Seas [M]. Qingdao: China Ocean University Press, 2005.

[3]蔡树群, 甘子均．南海北部孤立子内波的研究进展[J]. 地球科学进展, 2001, 16(2)： 215-219.

Cal S Q, Gan Z J. Progress in the study of the internal solition in the northern South China Sea[J]. Advance In Earth Sciences, 2001,16(2): 215-219.

[4]尤云祥, 石强, 缪国平.两层流体中大直径圆柱体的水动作用力[J]. 上海交通大学学报, 2005, 39(5)： 695-700.

You Y X, Shi Q, Miu G P. The Hydrodynamic forces on a large diameter cylinder in two layer fluid[J]. Journal of Shanghal Jiao Tong University, 2005, 39(5): 695-700.

[5]袁玉堂, 牟永春, 李冰.半潜式海洋平台的周期内波载荷分析[J]. 船海工程, 2012, 41(4)： 142-146.

Yuan Y T, Mu Y C, Li B.Periodical Internal Wave Load Analysis for the Semi-submersible Platform Ship & Ocean Engineering, 2012, 41(4)： 142-146.

[6]Arntsen O A. Disturbances, lift and drag forces due to the translation of a horizontal circular cylinder in stratified water[J]. Experiments in Fluids,1996, 21: 387-400.

[7]周喜武. 分层流体中Rankine卵形体生成的内波[D]. 青岛： 中国海洋大学, 2002.

Zhou X W. Stratified fluid Rankine ovoid generated internal waves[D].Qingdao: Ocean University of China, 2002.

[8]Xu Z T, Zhou X W, Chen X. Drag increment due to internal waves generated by Rankine ovoid[J]. Progress in Natural Science, 2002, 12(11): 849-853.

[9]徐肇廷, 陈旭, 吕红民, 等. 内波场中水平桩柱波阻的试验研究[J]. 中国海洋大学学报, 2007, 37(1)： 1-6.

Xu Z T, Chen X, Lv H M, et al.Static Analysis of the Position Control of Midwater Trawl for Double Dragging[J].Periodjcal of Ocean University of China. 2007, 37(1)：1-6.

[10]蔡树群, 龙小敏, 甘子钧. 孤立子内波对小直径圆柱形桩柱的作用力初探[J]. 水动力学研究与进展, 2002, 17(4)： 497-506.

Cai S,Q Long X M, Gan Z J. Preliminary study of forces and torques exerted by internal solitons on small-diameter cylindrical piles [J]. Journal of Hydrodynamics, 2002, 17(4): 497-506.

[11]Cheng Y L, Li J C, An L S, Liu Y F. The induced flow field by internal solitary wave and its action on cylindrical piles in the stratified ocean[C]. Proceeding of the Fourth International Conference on Fluid Mechanics, Dalian, Ca，July 20-23, 2004.

[12]叶春生, 沈国光. 海洋内波对小尺度圆柱体作用的分析与计算[J]. 天津大学学报, 2005, 38(2)： 102-108.

Ye C S, Shen G G. Numerical Calculation and Analysis aout Internal Wave's Force on small Scale Cylinder[J]. Journal of Tianjin University, 2005, 38(2)： 102-108.

[13]尤学一, 李占. 密度层化流体波动场中小尺度水平圆柱体受力模拟[J]. 天津大学学报, 2008, 41(7): 854-898.

You X Y, Li Z. Simulation of Wave Force on Small-Scale Horizontal Cylinder in Density Stratification Sea Water Movement[J]. Journal of Tianjin University， 2008, 41(7): 854-898.

[14]Xie J, Jian Y, Yang L. Strongly nonlinear internal soliton load on a small vertical circular cylinder in two-layer fluids[J]. Applied Mathematical Modelling, 2010, 34(8): 2089-2101.

[15]徐小辉, 胡天群, 魏岗等. 周期性内波与潜体相互作用的试验研究[J]. 水动力学研究与进展， 2011, A辑26(2)： 186-193.

Xu X H, Hu T Q, WEI Gang. Experimental investigations on the interaction of internal waves with a submerged body in a stratified fluid[J], Chinese Journal of Hydrodynamics, 2011, A 26(2)： 186-193.

责任编辑陈呈超

Experimental Investigations on the Interaction of Periodic Internal Waves with a Horizontal Cylinder

GUO Hai-Yan, WU Kai-Feng, WANG Fei, MA Dong, WANG Xin-Chao

(College of Engineering, Ocean University of China, Qingdao 266100, China)

Abstract:The experimental investigations on the interaction between periodic internal waves and a horizontal cylinder in a stratified fluid is carried out. The periodic internal waves are generated by the flap type wavemaker, and at the same time, the related factors of internal waves are obtained through dyeing experiment with CCD system, which could capture the picture of flow field precisely;By use of force measuring system, the wave forces exerted by the internal waves on a horizontal cylinder are measured quantificationally, so their variations with the internal waves function and submerged depth are derived respectively, then the date of the experiments were transformed to the computer and processed. Experimental results show that the vertical force of cylinder will change along with the change of periodic internal waves, and the maximum value will change with depth. In the pycnocline, the main frequency of a cylinder’s horizontal force is twice the main frequency of vertical force, the shape of coupling the two directions force presents the number “8”.

Key words:internal waves; horizontal cylinder; force measuring system; the vertical force; the horizontal force

基金项目：❋ 国家自然科学基金项目(51279187)；中央高校基本科研业务费(201262005);山东省科技重大专项(2015ZDZX04003)资助

收稿日期：2014-10-12；

修订日期：2015-06-12

作者简介：郭海燕(1959-)，女，教授，博导。E-mail：hyguo @ ouc.edu.cn

中图法分类号：P731

文献标志码：A

文章编号：1672-5174(2016)05-111-08

DOI：10.16441/j.cnki.hdxb.20140187

Supported by National Natural Science Foundation of China (51279187); Fundamental Research Funds for the Central Universities (201262005)；Important Science & Technology Specific Projects of Shandorg Province(2015ZDZX04003)