“平均数的再认识”教学设计与思考

◇陈俊杉

“平均数的再认识”教学设计与思考

◇陈俊杉

“平均数的再认识”是北师大版教材五年级下册新增的一个内容，是在学生认识了平均数，能用自己的语言解释其实际意义的基础上进行教学的，目的是通过丰富的现实背景，让学生感受到平均数的实用价值，体会到它是一个灵敏的数，容易受到极端数据的影响，是反映一组数据集中趋势的统计量。

那么，在课堂中如何渗透数据分析观念，培养学生分析、处理数据的能力呢？在这节课的第一个环节中，我是借助教材中的主情境，通过几个问题来进行的。

课件出示：根据有关规定，我国对学龄前儿童实行免票乘车政策，即一名成年人可以携带一名身高不足1.2米的儿童免费乘车。

1.这个1.2米是怎么得来的？

2.要调查多少名6岁儿童的身高呢？

3.（出示北京市6岁儿童身高数据后）现在你觉得把免票线定在1.2米合适吗？

4.这个1.2米是不是能让所有6岁以下儿童都免费乘车呢？

5.这个1.2米是不是固定不变的呢？

借助学龄前儿童免票乘车的情境，让学生感受平均数并不是仅仅出现在课本上，它和我们的生活息息相关。在分析问题的过程中，感知平均数具有代表性，是反映一组数据集中趋势的统计量，却不代表其中某一个具体的数。

在生活中，我们需要用平均数来表示一组数的平均水平，但当数据中有极大或者极小数出现时，平均数会受其影响，代表性就不明显了。如何让学生体会极端值对数据的影响呢？下面是我在上课时的一个片段。

师：我们学校四年级的同学进行了一场精彩的课本剧表演比赛。下表是四年级同学参加课本剧比赛的成绩统计表，请你计算出每个班的平均得分，并为他们排名。

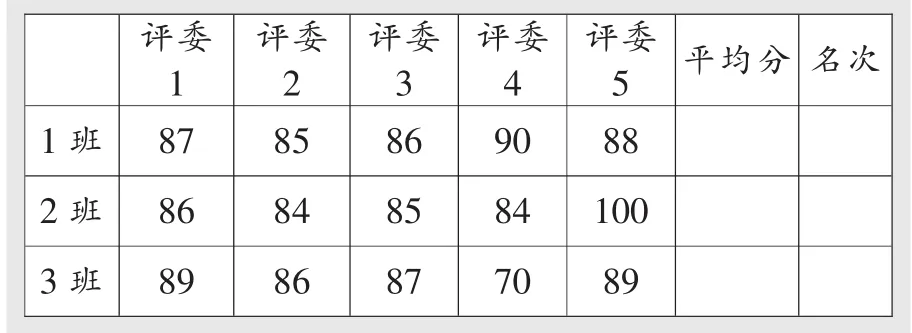
评委1评委2评委3评委4评委5 平均分 名次1班2班3班87 86 89 85 84 86 86 90 88 85 84 100 87 70 89

师：谁来汇报他们的平均分？

生：1班的平均分是87.2分，2班的平均分是87.8分，3班的平均分是84.2分。

师：排名情况如何？

生：第一名是2班，第二名是1班，第三名是3班。

师：但实际的排名情况刚好相反。得分最低的3班是第一名，得分最高的2班反而成了第三名。你们知道这是为什么吗？

（学生小声议论起来）

生：可能是在计算平均分的时候去掉了最高分和最低分。

师：是不是真像这位同学所说的呢？我们一起来看看，这是中央电视台青年歌手大奖赛的评分办法，我们采用的评分办法和它是一样的。

（播放视频并观看）

师：让我们也采用这样的评分办法，先去掉一个最高分，再去掉一个最低分，然后算一算每个班的平均分又是多少。

（生计算，然后汇报）

师：瞧，名次出现变化了。同学们，这两种评分办法，你觉得哪种合理呢？请小组讨论一下，说说自己的理由。

（有的同学认为第一种合理，也有的同学认为第二种合理）

师：我们请双方代表上台，辩论赛即将开始。先请正方（认为直接计算平均分合理的同学）说一说理由。

生1（正方）：我认为不能去掉最高分和最低分。因为分数是评委打出的，每个评委都打分了，不能随便去掉。

生2（反方）：我认为应该去掉。如果评委中有人和某个选手关系好，就可能给他多打分，对其他选手就不公平了。

生3（正方）：我认为不能去掉，如果选手本身很优秀，评委给他打出的高分被去掉了，也是不公平的。

生4（反方）：我也认为应该去掉，如果评委打的分数太低了，会把得分拉下来的。

（学生讨论激烈，双方争执不下）

师：看来大家各有道理。为了让大家更清楚地比较评委的打分，我们把这个表格制成复式条形统计图来看看。（如下图）

师：观察统计图，你发现了什么？

生1：从统计图上可以看出1班的得分情况，评委打分比较平均，平均分处于中间水平。

生2：2班的得分情况，评委5打的分比较高。

师：想一想，如果评委5打的分为85分左右，平均分会发生什么变化？

生3：平均分会比现在低一些。

师：评委5打的分可不止高了一点点，而是高出了很多，平均分会怎样？

生4：因为评委5打的分很高，平均分也被拉高了。

师：那也就是说，2班的平均分受谁的影响最大？

生5：受评委5打的分影响最大。

师：请观察3班的得分，平均分受谁的影响最大？

生6:受评委4的影响最大，评委4打的分太低了。

师：是啊，平均数非常灵敏，一组数中的任意一个数发生变化，平均数都会随之变化。

师：去掉一组数中这些很大或者很小的数，平均数会怎样呢？

生7：平均数就处于中间水平，就有代表性了。

（教师演示课件，帮助学生理解）

师：在这种情况下，你觉得这两种评分办法，哪一种更合理呢？

生：第二种更合理。

从师生对话中，我们可以看到，学生对于数据分析是有一定的基础的。

与此同时，为了帮助学生充分感受平均数的意义及在生活中的作用，体会到并不是所有情况下都需要去掉极端数据，在练习环节中，我设计了这样的对比判断。

下面两种评分办法公平吗？请说说理由。

（1）啦啦操比赛开始了。5位评委老师给五年级的啦啦操表演打分，分别是95分、92分、76分、99分、90分。计算5位评委打分的平均数，五年级表演的最后得分是90.4分。

（2）在30秒投篮比赛中，淘气前后5次投进的个数是7、15、20、21、17。求出5次进球数的平均数，淘气30秒投篮的进球水平是16个。

从课堂上学生的回答来看，大部分学生有这样的经验基础，能够判断出（1）是不公平的，（2）是公平的。但在理由的表述上不是特别清晰。

课后我在反思，也许是我选取的第（2）题不太合适，如果改为：期末考试结束了，淘气的语文成绩是95分，数学成绩是97分，英语成绩是84分，他这次期末考试的平均成绩是（95+97+84）÷3=92（分），那么学生在讨论计分公平与否时，可能会更加有话可说。

由此可知，数据分析是一个复杂的思维过程。教师要善于创造机会，启发学生自己想办法，使学生体会需要根据不同的背景，选择不同的方法，通过数据分析获得结论，从而培养其思维的灵活性。

（作者单位：北京师范大学厦门海沧附属学校）