基于多元t-copula模型的未决赔款准备金

胡晓伟，　刘　燕

(郑州大学 数学与统计学院　河南 郑州 450001)



基于多元t-copula模型的未决赔款准备金

胡晓伟，刘燕

(郑州大学 数学与统计学院河南 郑州 450001)

摘要：在非寿险精算领域中，单业务准备金的估计是研究的重点，而在非寿险公司对所有业务的总准备金水平进行评估时，不同业务之间存在着一定的相关性，将单业务的准备金进行简单的相加得到的总准备金往往大于实际理赔金额.因此，利用多元t-copula模型，从理论到实际数据等方面研究不同业务间的相关性，从而得出准备金的估计值，并通过风险边际的下降来说明在总准备金的估计中研究不同业务间的相关问题的必要性.

关键词：多元未决赔款准备金； t-copula模型； 相关性； 风险价值度

0引言

准备金的计提和管理是保险公司风险管理中非常重要的部分.非寿险公司的不同业务之间既非完全独立也非完全相关，将单业务的准备金进行简单的相加得到的总准备金往往会大于实际理赔金额.文献[1]指出，当各业务的理赔变量之间存在相关性时，对总的理赔变量的均方误差的估计也会更加复杂.因此，人们开始着重于研究多元未决赔款准备金.一种思路是将一元链梯法扩展到多元的情况[2]，文献[3]在多元线性模型的基础上提出多元加法准备金模型，文献[4]给出其均方误差的计算.另一种研究思路是利用copula连接函数，将关于单个业务的赔款变量的一维模型作为边缘分布，再通过copula函数建立一个关于多业务赔款变量的多维联合分布模型，从而考察总的业务组合的未决赔款准备金问题.文献[5]利用正态copula在边缘分布是正态分布的假设下,研究了多个流量三角形之间的相关结构，并对总的准备金预测值进行了随机模拟.文献[6]利用t-copula研究了多个保险业务的总赔款之间的相关性，通过模拟的方法从理论上验证了多业务的赔款之间存在相关性会对总赔款额的风险价值产生影响.文献[7]从理论上研究了基于a-stable分布的copula方法及其在CDO定价中的应用.文献[8]用“D藤copula”来描述相关性关系的GAMLSS模型以及准备金的评估，同时还刻画了不同业务线之间的尾部相依性.文献[9]基于Copula-Kernel模型研究了保险公司的综合风险经济资本度量与配置.

本文利用文献[5]中多元正态copula模型的研究方法，同时为了更好地复合市场的“尖峰、厚尾”的特性，提出多元t-copula模型，利用不同业务的损失流量三角形，从理论和实际数据等方面研究不同业务间的相关性，并且计算出准备金的估计值，通过变异系数的大小可以判断出模型的稳定性，以及通过风险边际的下降来说明在总准备金的估计中研究不同业务间的相关性的必要性.

1copula模型

增量赔款的流量三角形的观测数据是按照历年t=i+j-1(t=1,2,…,n)的顺序发生的，可获得第m个子业务的流量三角形的增量赔款观测值Dm={xmij,1≤t≤n,t=i+j-1}，即流量三角形上三角数据，而未测增量赔款集合为(Dm)C={xmij,n+1≤t≤2n-1,t=i+j-1}，即流量三角形下三角数据，如表1.

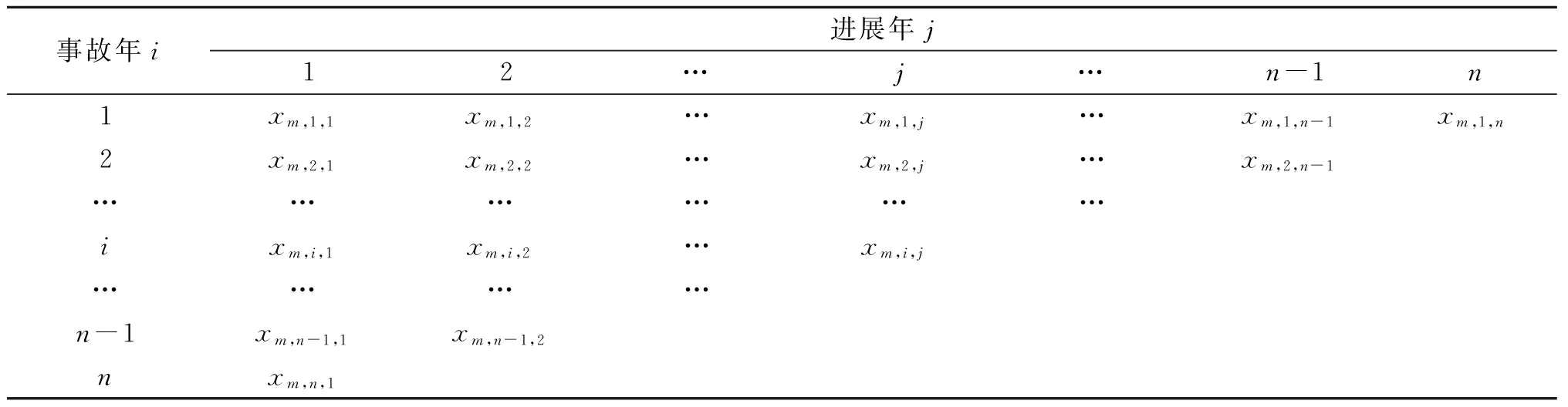
表1　第m个子业务的流量三角形

利用copula理论构建多元未决赔款准备金模型，需要考虑两个因素，边际分布和copula函数形式.

首先，假定第m个子业务的边际分布函数为Fm，则Fm(xmij)=ymij，m=1,2,…,M，ymij是流量三角形元素xmij的边际分布函数值.

其次，需要利用copula函数C来构造M个业务的增量赔款X=(X1,X2,…,XM)的联合分布，记为FX，即

FX(X1,X2,…,XM)=C(F1(X1),F2(X2),…,FM(XM))=C(Y1,Y2,…,YM),

其中：Xm=(xmij,i=1,2,…,n;j=1,2,…,n);Ym=(ymij,i=1,2,…,n;j=1,2,…,n).

2多元t-copula

2.1模型构造

对增量赔款xmij构造一个多元t-copula模型，即

(1)

其中:tp(·)是自由度为p的学生t分布函数，Σ是M×M维协方差矩阵，它的主对角线元素为1;tp,Σ表示自由度为p的多元t分布的联合分布函数.

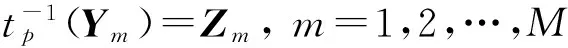
(2)

其中“∘”表示函数的复合运算.

通过(2)式的变换，可以将增量赔款的观测数据Xm一一对应的变换为服从t分布的变量Zm，将变换出的流量三角形的数据中的各个元素按照其对应的事故年i和进展年j记为zmij.

2.2因子分析

利用因子分析的思想，对变换后的变量zmij进行因子分析[10]，即

(3)

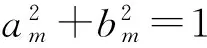
(4)

第m个流量三角形在同一个日历年t=i+j-1有共同因子βmt，它是由自由度p和不同的流量三角形的相关系数矩阵Σ决定的，而εmij是独立同分布的标准正态分布的随机变量，且各εmij与βmt互相独立，即

ε={εmij,m=1,2,…,M;i=1,2,…,n;j=1,2,…,n}～N(0,It).

其中It表示单位矩阵.

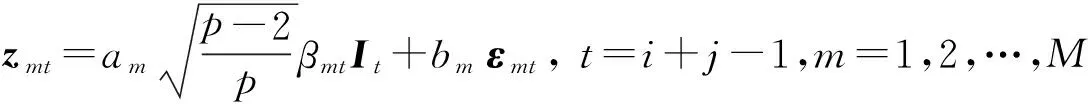
那么Kronecker乘积P⊗Q是一个mg×nf的矩阵，具体表示为

故向量Zt是服从均值为0、协方差矩阵如下的多元t分布：

(5)

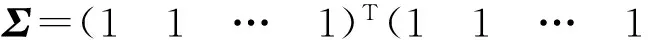
2.3模型估计

对于基于copula的多元准备金的随机模型，一般采用两阶段极大似然估计法.

第一步，利用常规的参数估计的方法估计边际分布的参数，如矩估计法和极大似然估计法，利用相关软件可以直接对边际分布模型进行拟合.

(6)

第二步，利用选择的copula函数，估计copula模型的有关参数，如公因子权重am，特殊因子权重bm，共同因子βmt以及相关系数矩阵Σ.

对式(3)两边求均值，有

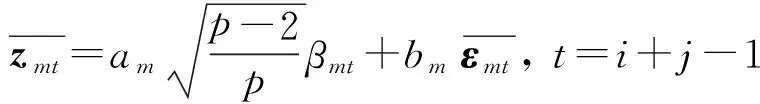
(7)

用式(3)减去式(7)，得

即

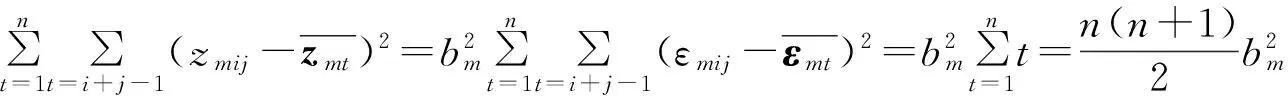
由此可以推出因子权重的估计量分别为:

进而得出

2.4准备金预测

第m个子业务的流量三角形在日历年t=n+1,n+2,…,2n-1的预期损失模型为:

Fm(xmt)=tp(am1tβmt+bmεmt), βt～N(0,∑), εmt～N(0,It),

其中:t=i+j-1；i=1,2,…,n;j=1,2,…,n；xmt, εmt元素分别为xmij,εmij的2n-t维向量；1t是所有元素均为1的2n-t维向量；It是(2n-t)×(2n-t)维单位矩阵.

(8)

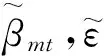
由此可以计算保险业务m的未来预期总的未决赔款及公司全部M个业务的总的未决赔款准备金，其分别为：

利用多次随机模拟的结果，就可以得出各业务以及公司整体的未决赔款准备金的分布情况.

2.5模型评价

由随机变量分布特点可知，如果只考虑保险公司准备金总量的期望值，可以直接将各业务的准备金的期望值直接相加，而准备金总量的方差，就必须要考虑各业务之间的协方差,

Var(X)=Var(X1)+Var(X2)+Var(X3)+2cov(X1,X2)+2cov(X1,X3)+2cov(X2,X3).

如果要考虑准备金总量的风险度量值，就不能将各业务准备金的风险度量值简单直接相加，各业务之间存在相关性，和的风险度量与各风险度量的和并不相等，并且还会存在较大的差异.常用的风险度量的方法有很多，如风险价值度、条件风险价值度、期望损失、条件尾部期望等，在本文将采用风险价值度度量方法.

风险价值度用VaR表示，在一段时间内，有u的把握，损失量不会大于V.u即为置信水平，V就是风险价值度VaR.即对于风险变量X，给定置信水平u∈(0,1)，则相应的风险价值度为

其中FX表示X的累积分布函数，VaR就是风险变量X在概率值为u点上的分位数.

用M(X)表示X的风险边际

M(X)=VaR[X,u]-E[X],

根据文献[11]对风险厌恶函数和风险价值度量方法的研究，基于VaR计算的风险边际M可以表示为：

M(X)=cov{X,φ∘F(X)}=σXσφρX,ρX=cor{X,φ∘F(X)},φ(v)=I{v=u},

其中：I{·}表示0-1示性函数，σX,σφ分别表示X和φ∘F(X)的标准差，ρX表示它们的相关系数.

3实例分析

3.1实际数据

本文研究使用的数据是文献[12]中我国某财产保险公司2010年起10个季度的增量赔款数据，数据包含3个保险产品的流量三角形，即M=3.这3种保险业务分别是机动车辆保险、企业财产保险和责任保险，其中机动车辆保险属于长尾业务，企业财产保险和责任保险都属于短尾业务.表2是对本文数据结构的直观展示，单位为元，表2中每个元素对应一个保险业务m在给定事故年i和进展年j的增量赔款额，每个事故年的3行元素对应的保险业务分别为：机动车辆保险、企业财产保险、责任保险.例如，表2内25 644表示机动车辆保险在第一事故年、进展年为1中的增量赔款，951 988表示企业财产保险在第一事故年、进展年为1中的增量赔款，45 263表示责任保险在第一事故年、进展年为1中的增量赔款.

本文分析和处理数据所用的软件为R和Excel.

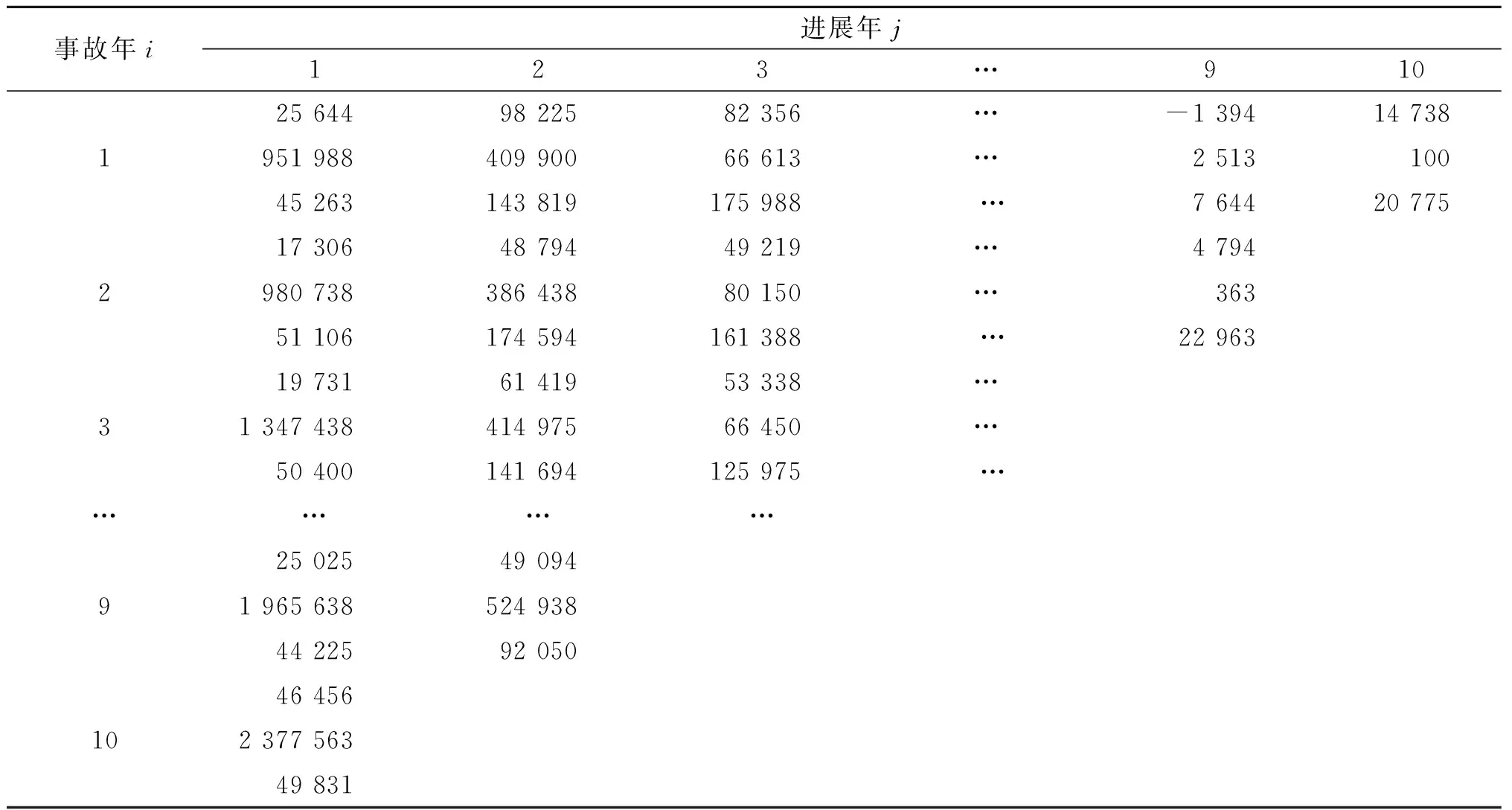
表2　3个保险业务的增量赔款

3.2拟合边缘分布

分别画出3个保险业务的增量赔款额的直方图，结果如图1所示：

从图1中可以看出，增量赔款的直方图与正态分布相差很远，假定对其所有数据求对数，可以看出其直方图近似服从正态分布，所以假设边际分布服从对数正态分布.为了避免待估参数过多造成过拟合，对增量赔款的均值只考虑列效应，即进展年j的效应.

建立对数正态模型，即

对参数μmj、σmj的估计结果如表3所示.

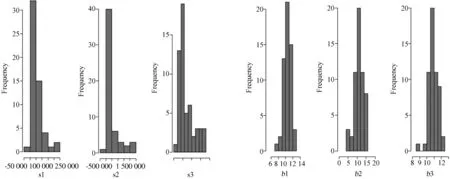
图1　3个保险业务的增量赔款额及其对数

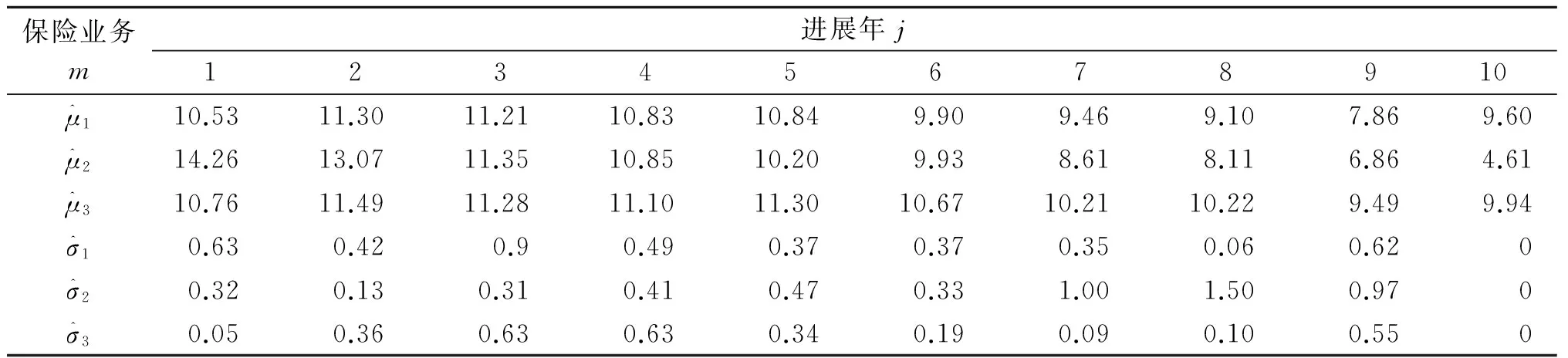
保险业务m进展年j1 2 3 4 5 6 7 8 9 10 μ^110.5311.3011.2110.8310.849.909.469.107.869.60μ^214.2613.0711.3510.8510.209.938.618.116.864.61μ^310.7611.4911.2811.1011.3010.6710.2110.229.499.94σ^10.630.420.90.490.370.370.350.060.620σ^20.320.130.310.410.470.331.001.500.970σ^30.050.360.630.630.340.190.090.100.550

3.3模型的估计与预测

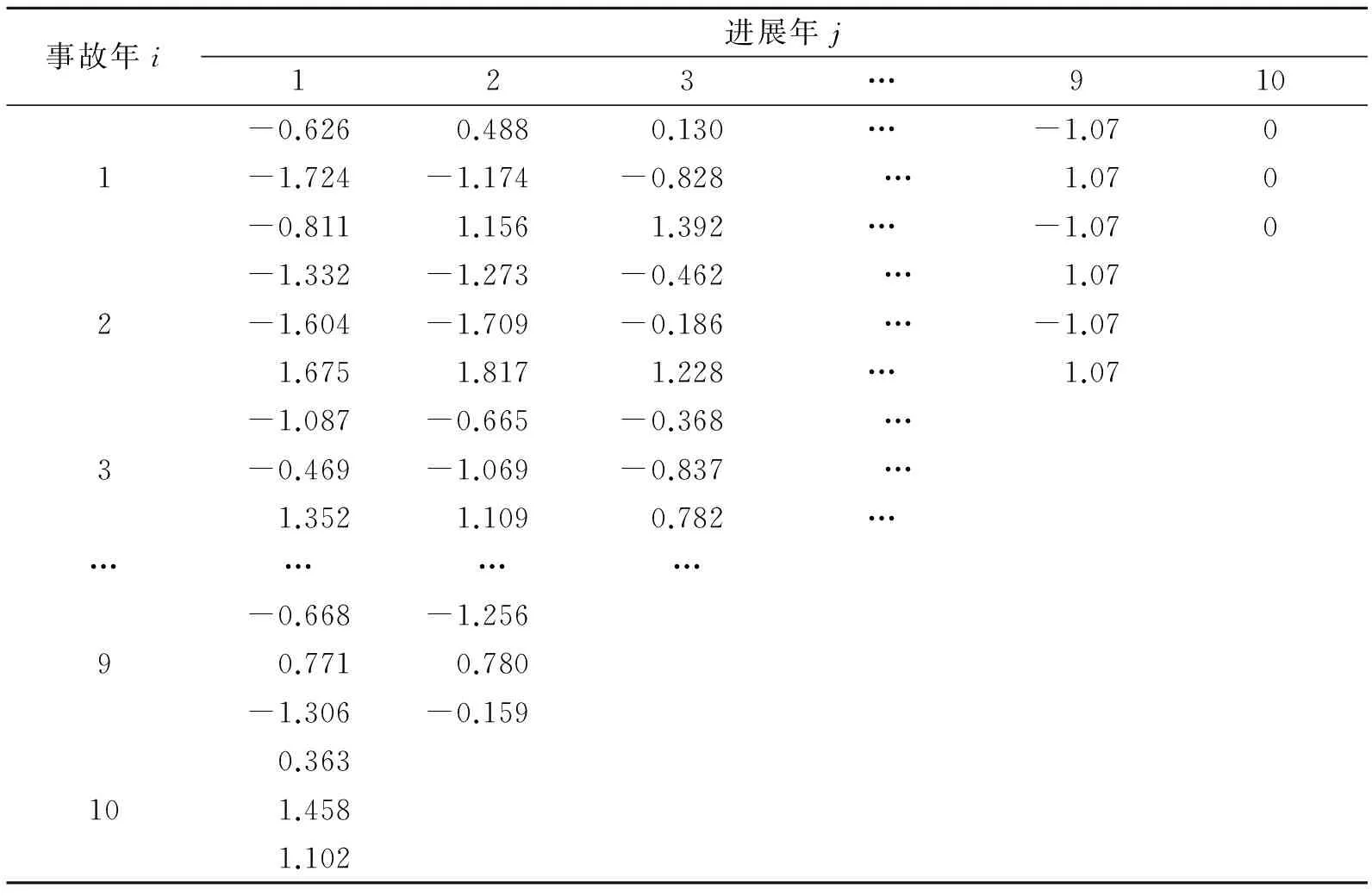
表4　3个保险业务的t分布的伪样本

由因子权重和公因子的估计式：

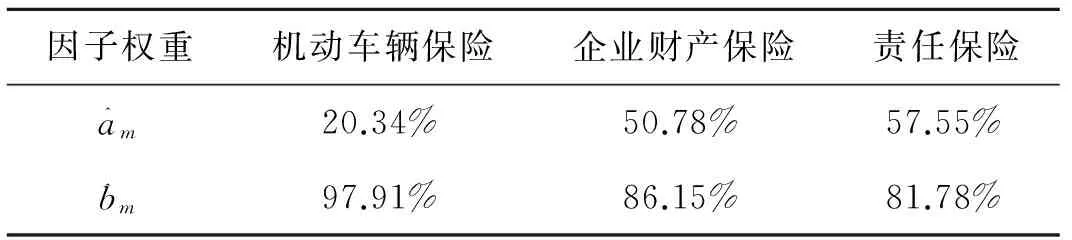
表5　因子权重估计结果

从表5可以看出共同度am最大的业务是责任保险，特殊方差bm最大的业务是机动车辆保险.

从表7可以看到，各业务之间都有一定的正相关或负相关性，说明将各业务的准备金的方差和风险边际进行简单的相加势必会对总的结果造成低估或高估.所以，考虑业务间的相关性是十分必要的.

表6　公因子的估计结果

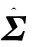
表7　多元t-copula模型的相关系数矩阵

利用未决赔款准备金的预测和评估方法，以及xmt的模拟值：

可以得到准备金的期望、方差和风险边际，模拟次数为10 000次，如表8.

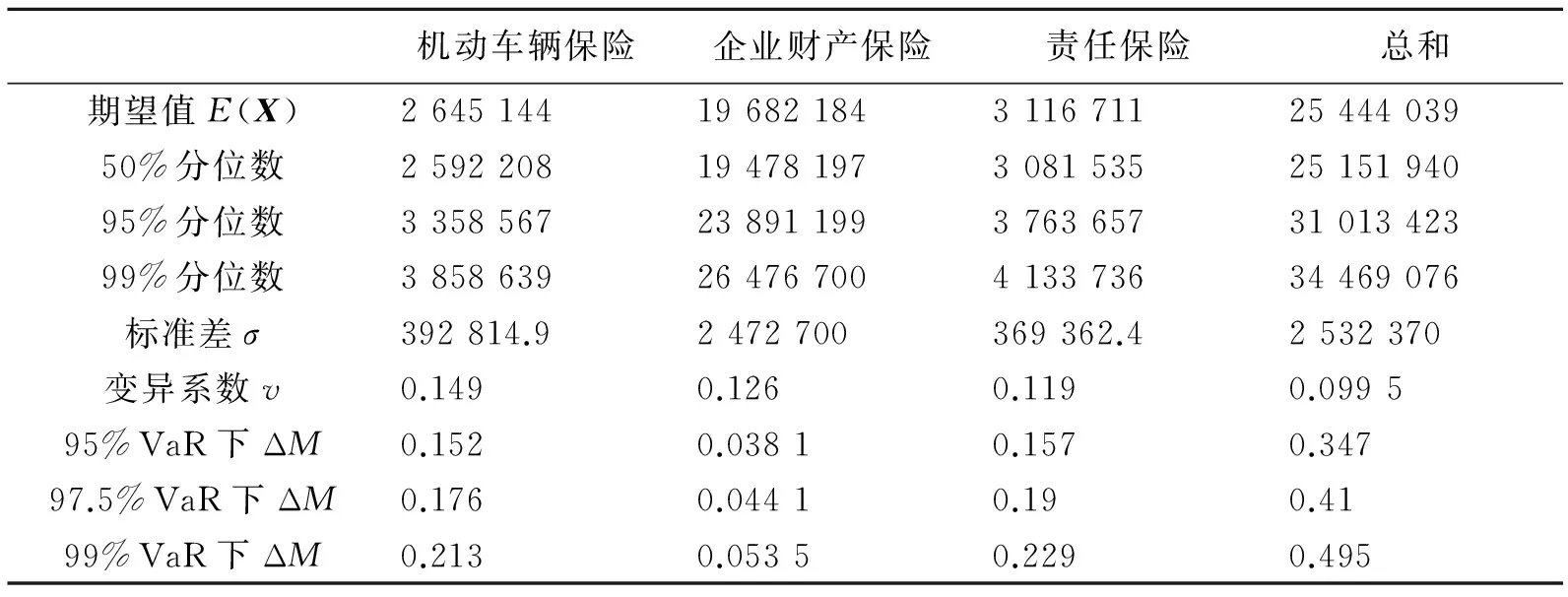
表8　未决赔款准备金的预测

4结束语

在评估非寿险保险公司整体业务的准备金总量水平时，需要考虑各业务间的相关性，利用copula连接函数，将关于单个业务的赔款变量的一维模型作为边缘分布，通过copula函数建立一个关于多业务赔款变量的多维联合分布模型.

在文中，利用文献[5]中多元正态copula模型的研究方法，建立了多元t-copula模型，利用因子分析以及求均值的方法对所有参数进行了估计，计算出各业务间的相关系数矩阵，再利用多次随机模拟的结果，得出各业务以及公司整体的未决准备金的分布情况.通过变异系数的大小判断出多元t-copula模型比较稳定，并且使用风险边际的下降比例说明在总准备金的估计中研究不同业务间的相关问题的必要性.

文中的不足之处就是t分布只有一个参数自由度p，可能在一些情况下对多变的市场情况模拟效果不理想，可以选择更加复杂的混合分布，来符合金融市场的“尖峰、厚尾、偏斜”的特性，例如在金融市场经常用到的双t因子copula模型、稳定因子copula模型、混合copula模型等.

参考文献：

[1]MERZ M，WIITHRICH M V．Prediction error of the multivariate chain ladder reserving method[J]．North american actuary，2008，12(2)：175—197．

[2]ZHANG Y W.A general multivariate chain ladder model[J].Insurance:mathematics and economics,2010,46(3):588—599.

[3]SCHMIDT K D.Optimal and additive loss reserving for dependent lines of business[J]．Casualty actuarial society forum．2006,100(4)：319—351．

[4]MERZM，WTITHRICH M V.Prediction error of the multivariate additive loss reserving method for dependent lines of business[J]．Variance．2009，3(1)：131—151．

[5]JONG P D．Modelling dependence between loss triangles using copulas[J].North American acturial journal,2009,16(1):74—86．

[6]梁冯珍，史道济．基于copula函数的保险准备金的确定方法[J]．统计与决策．2006，12(2)：142—144．

[7]ZHANG B, Li S.Collateralized debt obligation pricing with an a-stable copula[J]. Business computing and global information. SI AM Review, 2011，7(4):122—125.

[8]刘新红，孟生旺．基于藤 Copula 的 GAMLSS 模型与非寿险准备金评估[J]．经济数学，2014，4： 68—74.

[9]王依晨. 基于Copula-Kernel模型保险公司综合风险经济资本度量与配置研究[D]. 厦门：厦门大学，2014.

[10]约翰 C.赫尔 (John C.Hull). 风险管理与金融机构(第三版)[M]. 北京：机械工业出版社. 2012.

[11]CHOO W D JONG P.Loss reserving using loss aversion functions[J]．Insurance,2009，45(2):271—277．

[12]吴妮娜. 自助法和秩相关法在非寿险准备金总量评估中的应用[D]. 北京：中国人民大学. 2010.

(责任编辑：方惠敏)

The Reserving for Outstanding Losses Based on Multivariatet-copula Model

HU Xiaowei,LIU Yan

(DepartmentofMathematicsandStatistics,Zhengzhouuniversity,Zhengzhou450001,China)

Abstract:In the non-life insurance actuarial field, people focus on the study of the single business reserve estimates rather than on the evaluation total reserve of all the business’s level.There is a certain relationship among different business. simple summing reserves of all single businesses The total reserves by greater than the actual amount of claims tended to be.The tolal reserves estimates were drawn after using multivariate t-copulas model in exploring the correlation among different types of businesses.The finding of the deline of marginal risk showed that,it was necessary to explore the correlation among different types of businesses in the study of total reserve estimates.

Key words:multivariate reserving for outstanding losses；t-copula model；correlation；VaR

收稿日期:2015-09-24

基金项目:国家自然科学基金资助项目(10901143)．

作者简介:胡晓伟(1991—)，女，河南南阳人，硕士研究生，主要从事金融工程与保险精算研究，E-mail:1051162848@qq.com；通讯作者：刘燕(1978—)，女，河南开封人，副教授，博士，主要从事金融工程与保险精算研究，E-mail:liuyan@zzu.edu.cn．

中图分类号：F840

文献标志码：A

文章编号：1671-6841(2016)01-0001-09

DOI:10.3969/j.issn.1671-6841.201509027

引用本文：胡晓伟，刘燕.基于多元t-copula模型的未决赔款准备金[J].郑州大学学报(理学版),2016,48(1):1—9.