页岩气吸附解吸效应对基质物性影响特征
2016-06-13王敬罗海山刘慧卿林杰李立文林文鑫中国石油大学北京石油工程教育部重点实验室DepartmentofPetroleumGeosystemsEngineeringTheUniversityofTexasatAustin中国石油华北油田公司西南石油大学地球科学与技术学院
王敬,罗海山,刘慧卿,林杰,李立文,林文鑫(. 中国石油大学(北京)石油工程教育部重点实验室;. Department of Petroleum & Geosystems Engineering, The University of Texas at Austin;. 中国石油华北油田公司;. 西南石油大学地球科学与技术学院)
页岩气吸附解吸效应对基质物性影响特征
王敬1,罗海山2,刘慧卿1,林杰3,李立文3,林文鑫4
(1. 中国石油大学(北京)石油工程教育部重点实验室;2. Department of Petroleum & Geosystems Engineering, The University of Texas at Austin;3. 中国石油华北油田公司;4. 西南石油大学地球科学与技术学院)
摘要:为了研究页岩气降压开采过程中吸附气解吸作用对基质表观物性(如有效孔隙半径、有效孔隙度、表观渗透率)及气体流动机制的影响,推导了吸附解吸作用下页岩基质孔隙有效半径和表观渗透率动态模型,建立了考虑吸附解吸影响基质表观物性和气体传输机制的页岩气渗流数学模型。采用有限体积法对模型进行求解,利用实验及矿场数据验证了模型的可靠性,最后应用该模型研究了页岩气开采过程中基质物性参数、气体流动机制变化特征以及吸附效应对页岩气开发的影响规律。研究结果表明,页岩气开采过程中基质孔隙有效半径、有效孔隙度和表观渗透率逐渐变大,体积压裂改造区域流动机制由滑脱流转变为过渡流;忽略吸附层影响将导致地质储量和产气量严重高估;随着吸附层厚度增加,累计产气量变化不大,但采收率逐渐降低。图12表1参25
关键词:页岩气;吸附作用;解吸作用;基质孔隙;表观物性;气体流动机制;渗流模型
0 引言
页岩气的大规模开发影响世界天然气供给格局,预计到2020年,全球页岩气产量将达到4 000×108m3[1]。但是,页岩气开发难度巨大,因为页岩气藏渗透率极低,一般为10-9~10-6μm2,孔隙度低于10%[2]。页岩气孔隙尺寸非常小,据统计,半径小于10 nm的孔隙体积占总孔隙体积的42%,部分孔隙和流动通道半径甚至小于2 nm,只有少量的孔隙半径大于50 nm[3-4]。页岩气藏为典型的自生自储气藏,气体主要以自由气和吸附气的形式贮存于气藏中,吸附气含量达20%~80%,吸附气必须首先发生解吸才能开采出来[5-6]。由于页岩孔隙尺寸为纳米级,且大量的气体吸附在孔隙表面,气体分子流动和吸附气解吸过程同时进行,因此,页岩气在基质孔隙中的传输机理复杂,既要受到孔隙尺寸、孔隙压力的影响,又要受到吸附、解吸过程影响,从而最终影响页岩气开采。目前,大量研究中没有考虑吸附气对页岩孔隙尺寸的影响,一方面导致地质储量被高估[7-8],另一方面无法考虑页岩气藏开采过程中吸附、解吸效应对页岩表观物性和气体流动机制的影响。
本文首先推导了吸附、解吸作用下的页岩基质孔隙有效半径和表观渗透率动态模型,据此建立了考虑吸附、解吸效应对基质表观物性和气体传输机制影响的页岩气渗流数学模型,然后采用有限体积法对耦合模型进行求解、验证,最后应用该模型研究吸附、解吸过程中基质物性参数变化特征、气体流动机制变化特征以及吸附效应对页岩气开发的影响。
1 基质孔隙中页岩气分布特征及流动机理
如图1所示,基质孔隙中气体主要包括自由气、吸附气两部分。大量研究表明[9-10],页岩气吸附规律符合描述单层吸附的Langmuir模型,则饱和吸附状态下有效半径Re为孔隙绝对半径R0与甲烷分子直径dCH4之差,随着气体采出,孔隙压力降低,孔隙表面的吸附气发生解吸并参与流动,吸附层厚度变薄,有效孔隙半径变大。由于页岩气基质孔隙尺寸较小,所以气体分子表面吸附、解吸所导致的有效半径变化对基质表观物性造成的影响不能忽略。

图1 页岩气在基质孔隙中分布示意图
图2为基于努森数Kn划分的气体流动机制,努森数定义为气体分子平均自由程与孔隙平均直径之比[11-12]:

当Kn≤10-3时,气体流动为达西流;当10-3< Kn≤10-1时,气体流动为滑脱流;当10-1

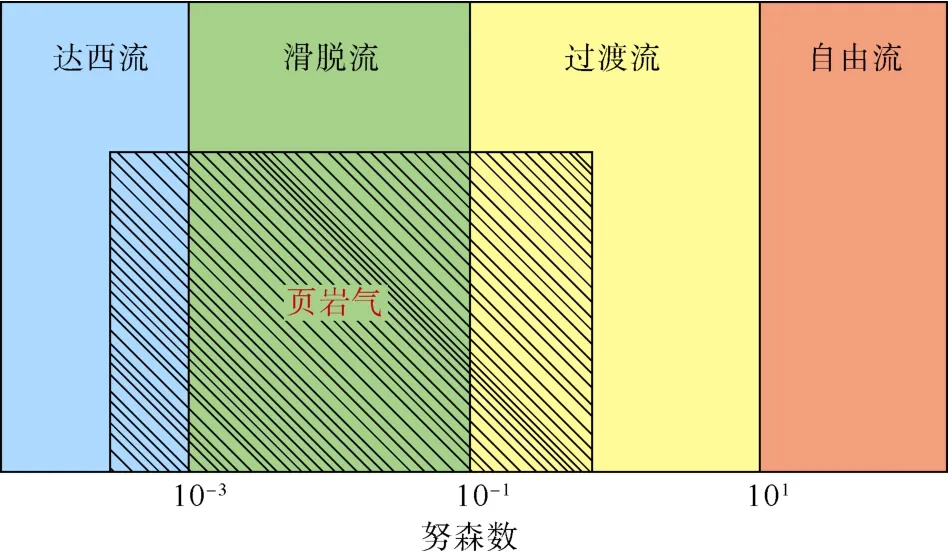
图2 气体流动机理划分
2 页岩气渗流数学模型
2.1物质守恒方程
为了建立页岩气渗流数学模型,提出以下假设:①页岩基质孔隙为球形;②页岩气藏不含水,或为束缚水条件且束缚水对吸附气没有影响;③页岩气吸附符合Langmuir模型;④气藏为等温系统,不考虑能量交换;⑤页岩气吸附解吸瞬间达到平衡。则页岩气在纳米级孔隙中渗流的质量守恒方程可表示为:

2.2页岩气渗流表观渗透率模型
气体在纳米孔中的渗流机制包括达西流、滑脱流、过渡流和自由流,Shi等[13]推导了涵盖这几种流动机制的表观渗透率表达式:

但是,由于气体分子吸附在孔隙表面,导致基质孔隙绝对渗透率降低,因此,基质绝对渗透率是吸附量的函数,则(4)式应变形为:
同时,在页岩气解吸过程中,孔隙有效半径不断变化,近而影响努森数。页岩储集层微观孔隙结构研究发现,有机质孔隙为近球形或椭球形[14-15],因此近似将页岩基质孔隙看作球形,则无吸附气状态下单个孔隙的体积为:

饱和吸附状态下,单个孔隙的有效体积为:

由(6)式和(7)式可得:
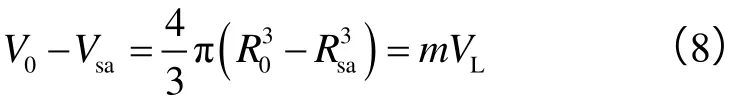
由于页岩气在基质孔隙中服从Langmuir吸附定律,则

联立(8)式和(9)式可得:

因此,任意压力下的有效孔隙半径为:
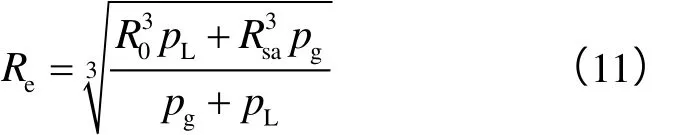
气体分子平均自由程为[11-12]:

联立(11)式、(12)式可得努森数表达式为:
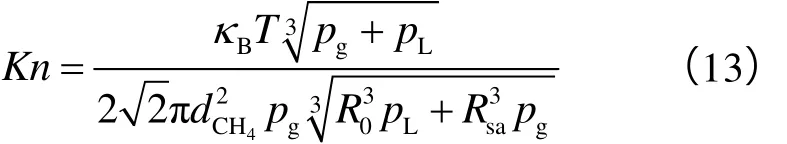
无吸附气时孔隙半径可由Carman-Kozeny方程求得[16-17]:
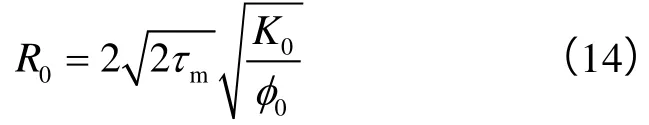
大量研究表明,页岩孔隙的吸附能力受到众多因素的影响,如有机质含量、黏土矿物含量、孔隙迂曲度以及比表面积等[18-19],因此,吸附气含量可能低于或高于理想状态下的单层吸附气量,为此,引入系数α校正饱和状态下吸附层厚度,则饱和吸附状态下的孔隙有效半径为:

该式反映了实际单层饱和吸附量与理想单层饱和吸附量的差别,理想饱和单层吸附时α=1;迂曲度大或比表面积大等因素可能导致实际单层吸附量高于理想光滑孔隙表面吸附量,此时α>1;有机质含量低或黏土矿物少等因素可能导致实际单层吸附量低于理想光滑孔隙表面吸附量,此时α<1;总体来说,α接近于1,其值通过拟合吸附实验参数获得。
同时,基质有效孔隙度可根据(9)式求得:

因此,联立(5)式、(11)式、(14)式、(16)
式可得到页岩气生产过程中基质表观渗透率的表达式:
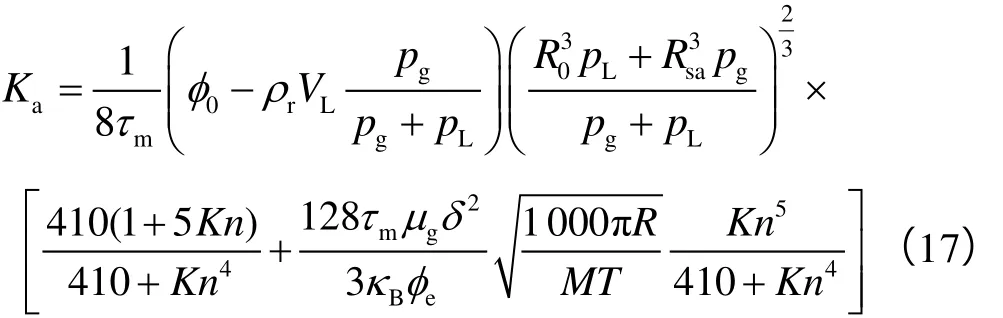
2.3吸附解吸效应
Ambrose等[6]的分子动力学实验研究表明,孔隙表面吸附气处于超临界状态,其密度约为自由气密度的1.8~2.5倍,因此单位体积岩石吸附的气体质量表达式为:

3 数学模型求解及验证
3.1数学模型求解
页岩气渗流数学模型为复杂的耦合方程系统,为了提高计算效率、精度和稳定性,本文采用有限体积隐式方法求解数学模型,(3)式可变形为:

其中

由于(20)—(23)式中大多数参数或变量均为压力的非线性函数,所以采用N-R方法(Newton-Raphson方法)进行求解,(20)式可写为:

其中

应用N-R迭代并给定残余向量R,则
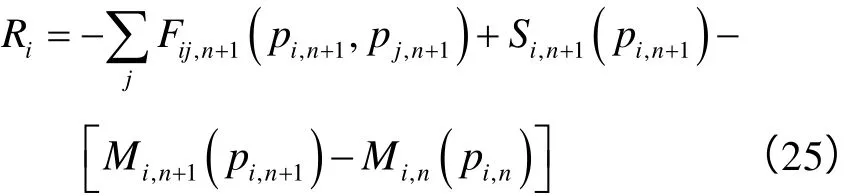
则稀疏雅克比矩阵J可以通过下面方法求得:

计算得到R和J后,便可以求解线性代数方程组:

求解后,pk, n+ 1可通过下式求得:

3.2模型验证
本文分别采用物理实验数据和矿场生产数据验证了模型的可靠性。首先应用Roy等[20]和Civan等[21]验证气体渗流模型所采用的实验数据[22]验证模型的可靠性。气体微尺度流道流动实验在5个注入压力下(135 kPa、170 kPa、205 kPa、240 kPa和275 kPa)注入气体,出口压力设定为100.8 kPa,测定微尺度流道沿程压力分布,模型参数参考文献[20]。根据上述参数采用建立的数学模型进行模拟计算并拟合,结果见图3,由此可见,计算值与实验值拟合效果较好。然后,应用Barnett页岩气藏一口典型井的实际数据进行了模型验证,生产数据及模型参数参考文献[23]。根据模型参数建模后,采用体积法计算地质储量,并与以往模型[24](不考虑吸附层影响)计算结果及采用Ambrose等[6]公式计算的理论地质储量进行对比(见表1),然后对该井开发过程进行数值模拟研究,拟合其产气速度(见图4),可见,新模型具有较好的可靠性。

图3 本文模型计算值与毛细管实验实测值对比(无因次距离为距注入端距离与毛细管长度之比)
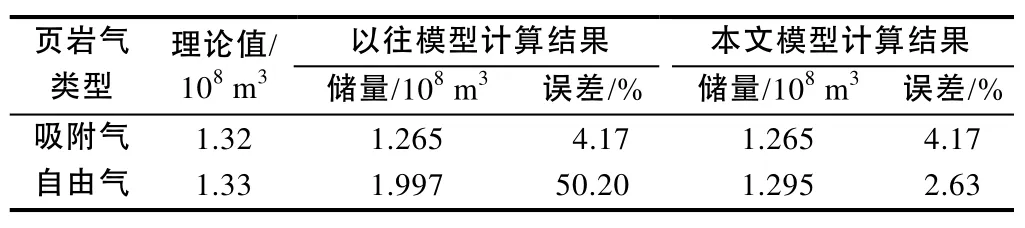
表1 页岩气储量计算结果对比

图4 Barnett页岩生产数据拟合结果
4 页岩气开发过程中基质表观物性参数变化规律
为了认识页岩气开发过程中页岩气吸附解吸效应对基质表观物性参数影响规律,使用上述拟合Barnett页岩生产数据得到的模型进行模拟研究,模型具体参数为:模型尺寸为890 m×436 m×90 m,埋深为1 600 m,地层压力为21.0 MPa,气藏温度为340 K,井底流压为3.5 MPa,绝对孔隙度为0.06,束缚水饱和度为0.7,岩石密度为2 580 kg/m3,孔隙迂曲度为1.1,基质渗透率为0.000 14×10-3μm2,微裂缝渗透率为2×10-3μm2,微裂缝间距为1 m;水力裂缝渗透率为1 000×10-3μm2,裂缝开度为0.003 m,裂缝间距为30 m,裂缝半长为40 m,裂缝高度为90 m,水平井水平段长度为890 m,页岩孔隙单层饱和吸附校正系数为1.3,吸附气与自由气密度之比为1.8,页岩气黏度为0.014 mPa·s,气体体积系数为0.004 6,甲烷分子直径为0.38 nm。
4.1基质表观物性变化特征
由于部分页岩气以吸附气的形式储存在岩石表面,导致气体有效流动通道减小,有效孔隙度降低,生产过程中,随着压力降低,吸附在孔隙表面的气体发生脱附,使有效流动通道和有效孔隙度逐渐升高[7,25]。图5、图6、图7分别为不同时间Barnett页岩水平井筒附近基质孔隙有效半径、有效孔隙度和表观渗透率分布。从图中可以出,初始条件下,页岩气藏基质有效孔隙度为0.045左右,仅为绝对孔隙度的75%左右;随着页岩气开采,吸附气从孔隙表面解吸,大量吸附气变为自由气,基质孔隙有效半径逐渐增大,有效孔隙度增加,表观渗透率变大,并且由于近井地带压力下降快,解吸量大,因此井筒周围表观物性变化明显。生产30 a后,基质孔隙有效半径增加5%左右,有效孔隙度大约增加10%,而表观渗透率增加1倍左右,由于页岩气的特殊流动机制,井筒周围表观渗透率远高于绝对渗透率。图8为不考虑吸附层对基质渗透率影响时渗透率分布,对比图7、图8可以看出,开采初期,不考虑吸附层影响时渗透率约为考虑吸附层影响时渗透率的1.5倍,随着吸附气解吸,吸附层变薄,其降低渗透率的作用减弱,开采至30 a时,不考虑吸附层影响时渗透率约为考虑吸附层影响时渗透率的1.3倍。

图5 不同时间Barnett页岩基质孔隙有效半径分布特征
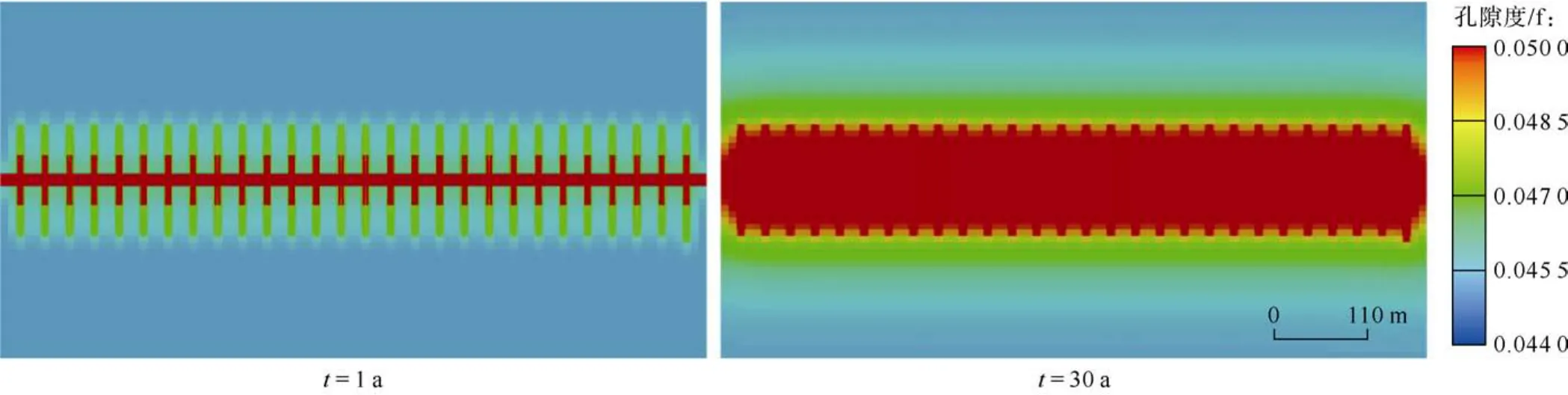
图6 不同时间Barnett页岩有效孔隙度分布特征

图7 不同时间Barnett页岩表观渗透率分布特征
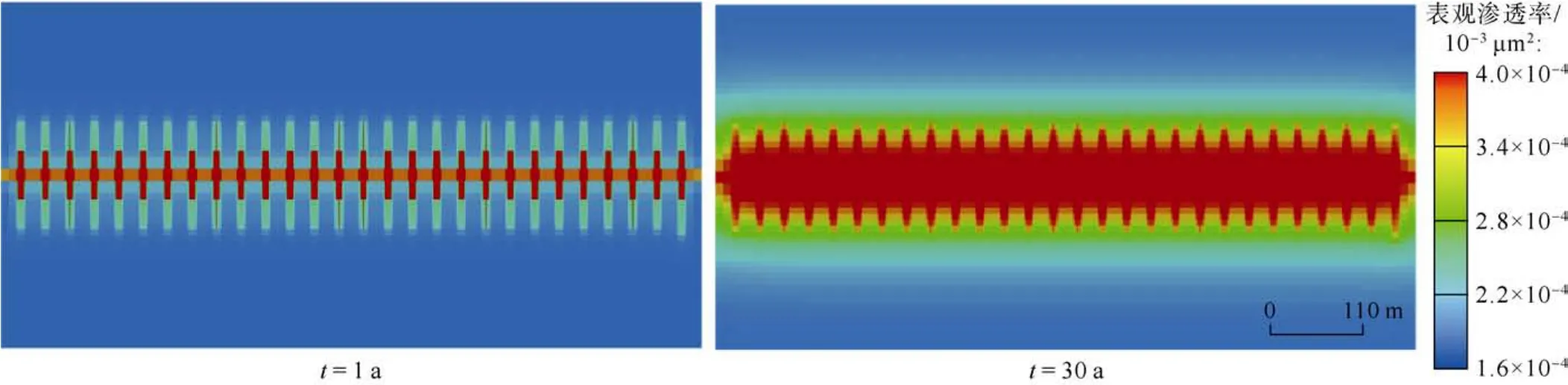
图8 不考虑吸附气影响时Barnett页岩表观渗透率分布特征
4.2 基质孔隙中流动机制变化特征
图9为开采30 a时气藏努森数分布,从图中可以看出,Kn为0.05~0.45,根据Kn对流动机制的判别标准,气藏中存在滑脱流和过渡流两种流动机制。图10为气藏开发过程中流动机制变化特征。从图中可以看出,页岩气开采过程中,Kn值逐渐变大,过渡流区域逐渐变大,即部分滑脱流区域转变为过渡流。原因在于,Kn值与压力、孔隙平均有效半径呈反比,孔隙压力降低会导致Kn值增加,孔隙平均半径增加会导致Kn降低,但是由于体积压裂区域压力大幅降低,压力起主导作用,随着页岩气采出,Kn值增加。
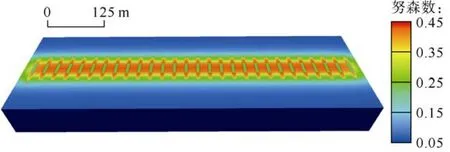
图9 t=30 a时气藏努森数分布特征

图10 Barnett页岩基质流动机制变化特征
4.3吸附气对页岩气开采影响特征
吸附层的存在影响基质孔隙度、渗透率以及气体流动机制,研究者往往忽略这一点,因此笔者研究了考虑吸附层影响和不考虑吸附层影响等多种情况下的产气量特征。根据地质参数建立地质模型并进行开发过程模拟计算,得到图11所示4种情况下的地质储量和累积产气量:忽略吸附气对孔隙度和渗透率的影响(即将吸附层看作虚拟体积,现行商业软件均采用该处理方法)时,地质储量为3.26×108m3,累计产气量约为1.35×108m3;仅考虑吸附层降低孔隙度,而忽略其对表观渗透率的影响,地质储量为2.56×108m3,累计产气量约为1.13×108m3;考虑吸附气对孔隙度和渗透率的影响,即实际页岩气藏的情况,地质储量为2.56×108m3,累计产气量约为1.08×108m3,采收率42.2%;如果气藏中气体仅以自由气形式存在,即致密气藏的情况,地质储量仅为2.00×108m3,累计产气量约为0.95×108m3,采收率47.5%。由此可见,将吸附层当作虚拟体积处理,会使地质储量被严重高估,导致计算产气量偏高;仅考虑吸附层对孔隙度的影响,虽然地质储量与实际页岩气藏情况相符,但是由于渗透率被高估,最终计算的产气量仍偏高;对比实际页岩气藏和致密气藏的情况可以发现,页岩气藏储量较高,但由于吸附气较自由气难以采出,所以最终采收率致密气藏高于页岩气藏。
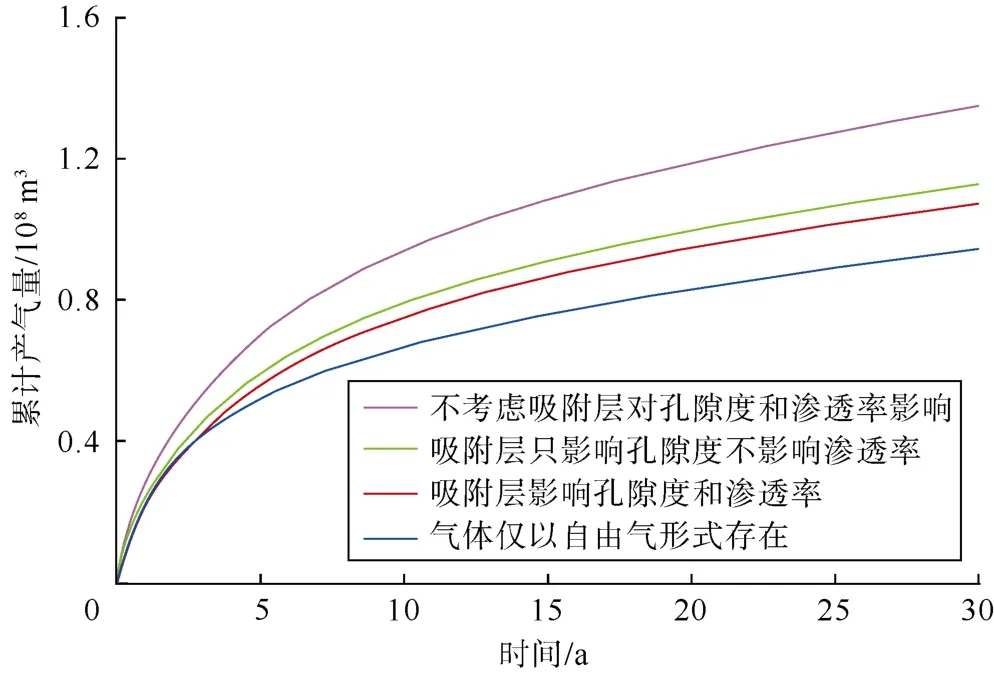
图11 吸附气对累计产气影响特征
4.4吸附层厚度对页岩气开采影响特征

图12 吸附层厚度对页岩气开采影响特征
图12为吸附层厚度对页岩气藏采收率和累计产气量的影响规律。饱和吸附层厚度为甲烷分子直径与饱和吸附校正系数乘积,从图中可以看出,随着饱和吸附校正系数增大,页岩气采收率逐渐降低,而累计产气量变化不大。原因在于,吸附层厚度越大,吸附气储量越大、自由气储量越小,但是由于吸附气密度大于自由气,所以相同孔隙度条件下,吸附层越厚,总地质储量越多,但吸附气比自由气难采出,所以最终累计产气差异不大,而采收率降低。
5 结论
基于页岩气在基质孔隙中的分布特征和吸附解吸规律推导了页岩吸附、解吸作用下的有效孔隙半径和表观渗透率动态模型,然后根据质量守恒定律建立了页岩气渗流数学模型,采用有限体积隐式法求解渗流模型,并利用实验及矿场数据验证了模型的可靠性。应用该模型研究表明:页岩气开采过程中基质孔隙有效半径、有效孔隙度和表观渗透率逐渐变大,体积压裂改造区域流动机制由滑脱流转变为过渡流;忽略吸附层对基质物性影响将导致地质储量和产气量严重高估;随着吸附层厚度增加,累计产气量变化不大,但采收率逐渐降低。
符号注释:
Aij——网格i与j的接触面积,m2;dCH4——甲烷分子直径,m;D——孔隙平均直径,m;De——有效孔隙直径,m;fij——网格i与j间的质量流量,kg/(m2·s);g——重力加速度,g=9.8 m/s2;Ga——页岩孔隙吸附能力,m3/kg;i——网格序号;j——与i网格相邻的任意网格序号;J——雅克比矩阵;Jij¢——雅克比矩阵中第i行第j¢个元素;Ka——页岩基质孔隙中气体流动表观渗透率,m2;K0——无吸附气时基质绝对渗透率,m2;K0c——考虑吸附气影响的校正的基质孔隙绝对渗透率,m2;Kn——努森数;lij——沿i到j的单位向量;m——单个孔隙体岩石质量,kg;m&——单位体积岩石吸附气体质量,kg/m3;mi——i网格的总质量密度,kg/m3;M——相对分子质量;n,n+1——本时刻和下一时刻;nij——网格i和j界面上的单位法向向量;nx——x方向网格数;ny——y方向网格数;pg——气相压力,Pa;pi,pj——i,j网格气相压力,Pa;pk,n+1——n+1时间步第k牛顿迭代步的压力,Pa;pL——Langmuir压力,Pa;qg——气相注入/采出速度,m3/(m3·s);R——气体常数,8.314 Pa·m3/(mol·K);R——残余向量;R0——无吸附气时孔隙半径,m;Re——有效孔隙半径,m;Ri——质量余量,kg; Rsa——饱和吸附状态下孔隙半径,m;si——第i个网格源汇项,kg/(m3·s);t——时间,s;T——温度,K;Tij——网格i与j间的传导率,kg/(m2·Pa·s);V0——无吸附气时孔隙体积,m3;Vsa——饱和吸附状态下孔隙体积,m3;Ve——某压力下孔隙有效体积,m3;VL——Langmuir体积,m3/kg;α——页岩孔隙单层饱和吸附校正系数;αd——吸附气与自由气密度之比;∆t——时间步长,s;∆Vi——第i个网格体积,m3;δ——气体分子碰撞直径,m,通常取甲烷直径;κB——Boltzmann常数,1.3806×10-23J/K;λ——分子平均自由程,m;μg——页岩气黏度,Pa·s;ρr——岩石密度,kg/m3;ρg——页岩气密度,kg/m3;τm——孔隙迂曲度;fe——有效孔隙度,f;f0——无吸附气时基质孔隙度,f;Fg——气体势函数,Pa。
参考文献:
[1] 邹才能, 董大忠, 王玉满, 等. 中国页岩气进展、挑战及前景(一)[J]. 石油勘探与开发, 2015, 42(6): 689-701.
ZOU Caineng, DONG Dazhong, WANG Yuman, et al. Shale gas in China: Progress, challenges and prospects (Ⅰ)[J]. Petroleum Exploration and Development, 2015, 42(6): 689-701.
[2] GHANIZADEH A, AQUINO S, CLARKSON C R, et al. Petrophysical and geomechanical characteristics of Canadian tight oil and liquid-rich gas reservoirs[R]. SPE 171633, 2014.
[3] AKKUTLU I Y, FATHI E. Multiscale gas transport in shales with local kerogen heterogeneities[R]. SPE 146422, 2011.
[4] ADESIDA A G, AKKUTLU I Y, RESASCO D E, et al. Kerogen pore size distribution of Barnett shale using DFT analysis and Monte Carlo simulations[R]. SPE 147397, 2011.
[5] CURTIS J B. Fractured shale-gas systems[J]. AAPG Bulletin, 2002, 86(11): 1921-1938.
[6] AMBROSE R J, HARTMAN R C, DIAZ -CAMPOS M, et al. New pore-scale considerations for shale gas in place calculations[R]. SPE 131772, 2010.
[7] HARTMAN R C, WEARHERFORD L, AMBROSE R J, et al. Shale gas-in-place calculations part II: Multi-component gas adsorption effects[R]. SPE 144097, 2011.
[8] SIGAL R F. The effect of gas adsorption on storage and transport of methane in organic shales[R]. New Orleans, Louisiana: SPWLA 54thAnnual Logging Symposium, 2013.
[9] 王香增, 高胜利, 高潮. 鄂尔多斯盆地南部中生界陆相页岩气地质特征[J]. 石油勘探与开发, 2014, 41(3): 294-304.
WANG Xiangzeng, GAO Shengli, GAO Chao. Geological features of Mesozoic continental shale gas in south of Ordos Basin, NW China[J]. Petroleum Exploration and Development, 2014, 41(3): 294-304.
[10] ROSS D J K, BUSTIN R M. Impact of mass balance calculations on adsorption capacities in microporous shale gas reservoirs[J]. Fuel, 2007, 86: 2696-2706.
[11] JAVADPOUR F, FISHER D, UNSWORTH M. Nanoscale gas flow in shale gas sediments[J]. Journal of Canadian Petroleum Technology, 2007, 46(10): 55-61.
[12] BIRD R B, STEWART W E, LIGHTFOOT E N. Transport phenomena[M]. Rev. 2nd ed. New York, USA: John Wiley & Sons Inc., 2002.
[13] SHI J T, ZHANG L, LI Y S, et al. Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting[R]. SPE 167226, 2013.
[14] 杨峰, 宁正福, 胡昌蓬, 等. 页岩储层微观孔隙结构特征[J]. 石油学报, 2013, 34(2): 301-311.
YANG Feng, NING Zhengfu, HU Changpeng, et al. Characterization of microscopic pore structures in shale reservoirs[J]. Acta Petrolei Sinica, 2013, 34(2): 301-311.
[15] 侯宇光, 何生, 易积正, 等. 页岩孔隙结构对甲烷吸附能力的影响[J]. 石油勘探与开发, 2014, 41(2): 248-256.
HOU Yuguang, HE Sheng, YI Jizheng, et al. Effect of pore structure on methane sorption capacity of shales[J]. Petroleum Exploration and Development, 2014, 41(2): 248-256.
[16] CARMAN P C. Flow of gases through porous media[M]. London: Butterworths Scientific Publications, 1956.
[17] CIVAN F. Effective correlation of apparent gas permeability in tight porous media[J]. Transport in Porous Media, 2010, 82: 375-384.
[18] ROUQUEROL J, ROUQUEROL F, SING K S W. Adsorption by powers and porous solids: Principles, methodology and applications[M]. London: Academic Press, 1999.
[19] SOLAR C, BLANCO A G, VALLONE A, et al. Adsorption of methane in porous materials as the basis for the storage of natural gas[M]. Rijeka: InTech Europe, 2010.
[20] ROY S, RAJU R, CHUANG H F, et al. Modeling gas flow through microchannels and nanopores[J]. Journal of Applied Physics, 2003, 93(8): 4870-4879.
[21] CIVAN F, RAI C S, SONDERGELD C H. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms[J]. Transport in Porous Media, 2011, 86: 925-944.
[22] PONG K C, HO C M, LIU J Q, et al. Non-linear pressure distribution in uniform micro-channels: Applications of microfabrication to fluid mechanics[J]. ASME Fluids Engineering Division, 1994, 197: 51-56.
[23] YU W, SEPEHRNOORI K. Simulation of gas desorption and geomechanics effects for unconventional gas reservoirs[R]. SPE 165377, 2013.
[24] CMG. GEM user guide[M]. Calgary, Canada: Computer Modeling Group Ltd., 2011.
[25] XIONG X, DEVEGOWDA D, MICHEL G G, et al. A fully-coupled free and adsorptive phase transport model for shale gas reservoirs including non-Darcy flow effects[R]. SPE 159758, 2012.
(编辑张敏)
Influences of adsorption/desorption of shale gas on the apparent properties of matrix pores
WANG Jing1, LUO Haishan2, LIU Huiqing1, LIN Jie3, LI Liwen3, LIN Wenxin4
(1. MOE Key Laboratory of Petroleum Engineering in China University of Petroleum, Beijing 102249, China; 2. Department of Petroleum & Geosystems Engineering, The University of Texas at Austin, Austin 78712, USA; 3. PetroChina Huabei Oilfield Company, Langfang 065000, China; 4. School of Geosciences and Technology, Southwest Petroleum University, Chengdu 610500, China)
Abstract:The adsorption/desorption effects impact the petro-physical properties of matrix pores during gas depressurizing production, such as effective pore radius, effective porosity, apparent permeability, which will further impact the gas flow regime. In this paper, the dynamic models of effective pore radius and apparent permeability under the action of gas adsorption/desorption are derived. The mathematical model of shale gas flow is established considering the effects of adsorbed gas on apparent properties and gas flow regime. After that, the model is solved and validated using a finite volume method and experimental and field data. Finally, the variations of apparent parameters of matrix pores and gas flow regimes during gas production, and the influences of adsorption on gas production are demonstrated. The results show that the effective pore radius, porosity and apparent permeability increase during gas production; the gas flow regime in stimulated reservoir volume (SRV) changes from slip flow to transition flow; if the impacts of adsorbed gas on gas production is overlooked, both original gas in place (OGIP) and gas production will be significantly overestimated. The cumulative gas production changes slightly as the adsorption layer thickness increases, but the gas recovery factor decreases.
Key words:shale gas; adsorption; desorption; matrix pore; apparent properties; flow regime; flow model
基金项目:国家重点基础研究发展计划(973)项目(2015CB250906);国家自然科学基金(51474226);中国石油大学(北京)科研基金(2462014YJRC028)
中图分类号:TE319
文献标识码:A
文章编号:1000-0747(2016)01-0145-08
DOI:10.11698/PED.2016.01.19
第一作者简介:王敬(1985-),男,河北武邑人,博士,中国石油大学(北京)石油工程学院讲师,主要从事油藏渗流机理、提高采收率、非常规油气开发等方面研究。地址:北京市昌平区府学路18号,中国石油大学(北京)石油工程学院,邮政编码:102249。E-mail:wangjing8510@163.com
收稿日期:2015-03-18修回日期:2015-12-10
