致密储集层应力敏感性评价

肖文联，李滔，李闽，赵金洲，郑玲丽，李铃（西南石油大学油气藏地质及开发工程国家重点实验室）

致密储集层应力敏感性评价

肖文联，李滔，李闽，赵金洲，郑玲丽，李铃
（西南石油大学油气藏地质及开发工程国家重点实验室）

摘要：通过对比分析表征岩石渗透率与有效应力关系的经验模型与理论模型，得到3种应力敏感系数（S、α、β）的表达式；结合实验数据和岩石微观结构特征，提出致密砂岩应力敏感性划分标准。用经验模型与理论模型分析致密砂岩和不同类型花岗岩渗透率与有效应力的实验数据，进一步明确经验模型以及应力敏感系数的物理含义，并计算岩石的3种应力敏感系数，仅S中不含不确定指数n，具有明确的物理意义。基于3种应力敏感系数特征、渗透率与有效应力关系的研究，发现可用应力敏感系数S划分储集层岩石的应力敏感性：S>0.40为强应力敏感性；S<0.25为弱应力敏感性；0.25≤S≤0.4为中等应力敏感性，强应力敏感性岩心更满足对数模型，弱应力敏感性岩心更满足指数模型和二项式模型，中等应力敏感性岩心满足乘幂模型。结合岩石的微观特征讨论了应力敏感性划分标准的适应性，发现强应力敏感性岩石裂缝性特征明显，而弱应力敏感性岩石具有孔隙性特征；此外，黏土胶结物的类型、岩石颗粒大小以及岩性也影响岩石的应力敏感性。图8表2参25

关键词：致密砂岩；应力敏感性；应力敏感系数；有效应力；渗透率；微观结构

0　引言

致密储集层油气资源丰富，将成为中国乃至全球油气资源二次扩展的主力储集层[1]。然而，致密储集层岩石矿物组成、孔隙结构等比较复杂[2-3]，导致油气资源开发过程中岩石渗透率随孔隙流体压力的变化规律（即渗透率应力敏感性）极其复杂。致密储集层岩石应力敏感性评价一直是研究热点[4-9]，但尚未形成统一认识。

国内外研究者[4-5,7-8]主要基于变围压实验建立渗透率与有效应力的关系，再结合有效应力方程[10-11]计算渗透率损害率和应力敏感系数，进而评价储集层岩石的应力敏感性。因而，有效应力的确定、渗透率与有效应力关系的建立对储集层岩石应力敏感性评价起着关键的作用。

渗透率与有效应力关系的表征常用乘幂模型、指数模型、二项式模型和对数模型，且不同类型岩石对应不同的关系模型[5,8,12-14]。尹尚先等[14]指出裂缝性岩石、孔隙性岩石和毛细管型岩石的渗透率与有效应力关系分别符合乘幂模型、指数模型和二项式模型，其中毛细管模型常被用于分析岩石应力敏感性。然而，Jones[13]、赵金洲等[12]和Dong等[8]分别发现裂缝性岩石、孔隙性致密砂岩和细粒砂岩分别用对数模型、二项式模型和乘幂模型表征效果最好，且Walsh[15]证明了基于裂缝平板模型得到的渗透率与有效应力表达式与对数模型一致。

国内学者通常依据行业标准SY/T 5358-2010[16]评价致密砂岩应力敏感性，认为致密砂岩一般都呈强应力敏感性，原因在于参照的有效应力不符合储集层实际情况。为此，一些学者修正了参照的有效应力，研究认为致密砂岩应力敏感性相对较小，甚至呈弱应力敏感性。国外学者常用经验模型拟合基于变围压实验的渗透率随有效应力变化的实验数据，计算乘幂模型、指数模型和对数模型的应力敏感系数S、α和β，进而分析岩石的应力敏感性。

综上所述，不同的应力敏感性评价方法得到的评价结果不同。本文从渗透率与有效应力关系的研究入手，认识应力敏感性系数的物理意义，再结合实验数据和岩石的微观结构特征，提出并分析致密储集层岩石应力敏感性划分标准。

1　应力敏感系数

常用4种经验模型表征渗透率与有效应力之间的关系[5,8,12-14]：乘幂模型、指数模型、二项式模型和对数模型，分别如下：

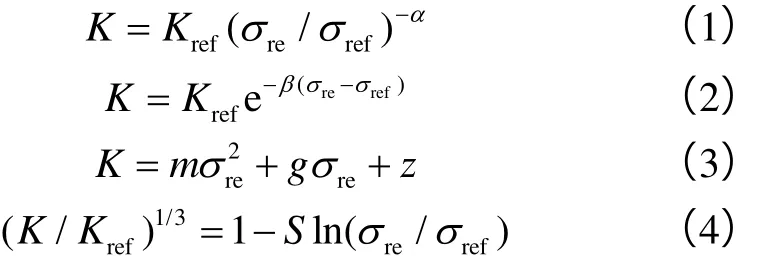
Walsh[15]推导得到了平板裂缝模型（W模型）（见图1a）渗透率与有效应力的表达式：

同理，分析发现分别基于圆形管束模型（见图1b）和椭圆形管束模型（见图1c）建立的渗透率与有效应力关系（6）式和（7）式[17-18]与二项式模型一致。

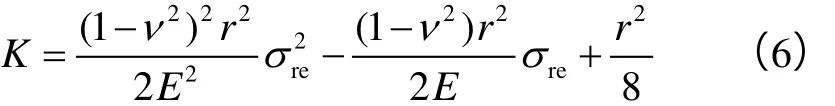
图1　各模型的孔隙形状示意图

二项式模型（（3）式）中的拟合参数仅与岩石的孔隙结构和弹性参数有关。当ε等于或者接近1.0时，椭圆形管束模型与圆形管束模型相同且与二项式模型一致，对应岩石表现为孔隙性岩石的特征；当ε远小于1.0时，椭圆管束模型与二项式模型一致，对应岩石表现出裂缝性岩石的特征，且随ε减小裂缝特征越来越明显。

星形管束模型（GP模型）（见图1d）也被用于描述孔隙性岩石渗透率与有效应力关系[6]，其表达式[19]如下：

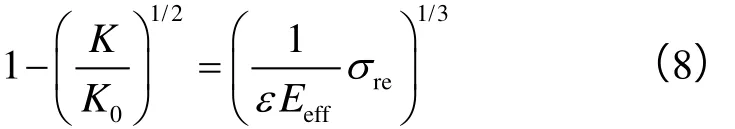
将（8）式左边渗透率项的幂指数2改写为n（n为正整数）得到（9）式（GPn模型）：

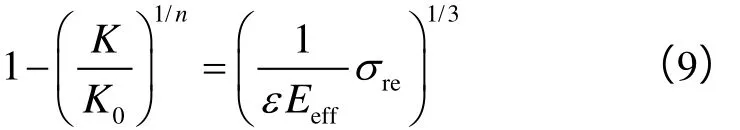
当n为无穷大时，得到（10）式：

指数模型（（2）式）可改写为：

将（11）式两边同时取对数，并借助极限函数（（12）式），得到（13）式：

对比（10）式和（13）式，得到β=n/(εEeff)。国外学者一般采用星形管束模型描述孔隙性岩石，这与尹尚先等[14]的观点一致，即指数模型适于表征孔隙性岩石渗透率与有效应力的关系。

同理，将（5）式中渗透率项的幂指数“3”改写为“n”得到Wn模型（（14）式），基于极限函数（12）式推导得到与乘幂模型表达形式相同的（15）式：

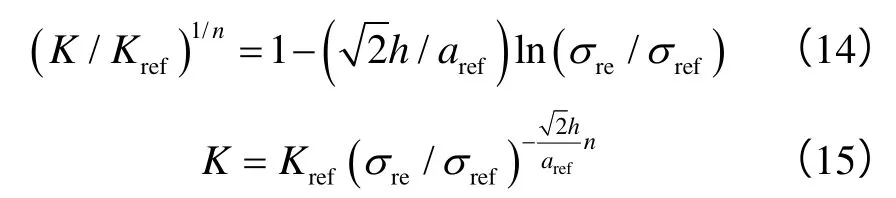
由此可见，经验模型都有与之对应的理论模型，应力敏感系数的表达式中含有岩石结构参数、弹性参数等，说明岩石的微观结构特征是影响应力敏感性的根本原因；然而，除了应力敏感系数S以外，应力敏感系数β和α中都含有不确定指数n。

2　应力敏感性特征

结合4块人造裂缝花岗岩（裂缝面抛光岩心Barre P、0.023 mm砂纸磨裂缝面岩心Barre 600、0.120 mm砂纸磨裂缝面岩心Barre 120和张力断裂缝岩心Barre T）[20-21]、3块天然微裂缝花岗岩（Chelmsford G、Chelmsford R和Chelmsford H）[11,20]和27块致密砂岩[20,22-23]的有效应力实验数据，进一步分析渗透率与有效应力关系的经验模型（二项式模型、指数模型、乘幂模型和对数模型）和理论模型（W模型、Wn模型、GP模型及GPn模型），并计算应力敏感系数。渗透率数据在高围压和高孔隙压力条件下测试，克服了以往低孔隙压力（接近大气压）、变围压应力敏感实验的不足（该实验压力与地层条件不符，气测渗透率时可能存在较严重的滑脱效应影响等），最为关键的是可直接计算岩石的有效应力（σre=pc-κpp），进而可避免依据Terzaghi有效应力方程（σre=pc-pp）计算而出现的错误——Terzaghi有效应力已被证明不能表征致密砂岩[20,22-23]。

表1给出了采用不同模型拟合实验数据的相关系数R2，R2值越大，拟合效果越好，说明对应模型更适合表征岩心渗透率与有效应力的关系，对数模型与W模型（（4）式和（5）式）拟合效果相同。指数模型与GP模型拟合得到的R2值具有相似的变化特征；当GPn模型拟合得到n=1.0（Wn模型拟合得到n小于1.0）时，指数模型与GP模型拟合得到的R2值接近1.0，说明指数模型与GP模型的相关性好，且满足指数模型和GP模型岩心的应力敏感系数β仅与岩石的孔隙结构参数有关，具有明确的物理意义；此时二项式模型拟合得到的R2值也接近1.0。当Wn模型拟合得到n≈3时，W模型（对数模型）与乘幂模型拟合效果一致；当Wn模型拟合得到n远大于3（即为∞）时，乘幂模型与Wn模型拟合效果一致且最好，则满足乘幂模型岩心的应力敏感系数α中除了包含岩石孔隙结构参数之外，还有不确定的指数n，说明α不具有明确的物理意义。特别需要指出的是，W模型拟合得到的R2值基本都大于0.950 0，且该模型中的应力敏感系数S仅与岩石的微观结构参数有关，因此S适宜作为应力敏感性大小划分的参数。

表1　模型拟合相关系数

利用指数模型、乘幂模型和对数模型分别拟合实验数据，计算得到应力敏感系数（见表2）。S-β和S-α的关系见图2、图3。随着S的增加，β和α均逐渐增大；致密砂岩、天然微裂缝花岗岩和人造裂缝花岗岩的应力敏感系数变化特征不同。当S小于0.25或者大于0.60时，砂岩S-β具有较为明显的线性相关性。当S小于0.40（α小于1.0）时，砂岩S-α的线性相关性特征明显。当S大于0.40时，部分砂岩的S-α趋势线与人造裂缝花岗岩的S-α趋势线一致，对应砂岩满足乘幂模型或W模型（见表1）；其余砂岩满足指数模型和二项式模型（见表1），与微裂缝花岗岩的S-α趋势线一致。因此，满足乘幂模型或W模型砂岩的应力敏感性强于满足指数模型和二项式模型砂岩的应力敏感性。

表2　3种应力敏感系数计算结果

图2　应力敏感系数S-β关系图

图3　应力敏感系数S-α关系图

为进一步分析致密砂岩的应力敏感性，在双对数坐标下绘制了无因次渗透率K/Kr与有效应力的关系曲线（见图4），可见渗透率与有效应力的关系曲线表现为3种曲线簇：图4b曲线簇中的曲线都接近直线，且曲线的波动幅度很小，符合乘幂模型（α≈1.0）的曲线形态特征，对应岩心的S值为0.256～0.418；对于S大于0.418的岩心，其组成的曲线簇向下弯曲（见图4a），符合W模型的曲线形态特征；对于S小于0.256的岩心，其曲线簇中曲线较为分散（见图4c），规律性较前两种差，以指数模型或二项式模型岩心为主。同时，S=0.418和S=0.256恰好分别落在S-α和S-β相关性强与弱的分界处（S-β相关性强与弱的另一个分界处S约为0.6）。因此，取S=0.25和S=0.40作为3种曲线簇划分的标准，并将应力敏感性划分为强、中、弱；当S大于0.6时，岩心表现出的应力敏感性更为显著，这与Jones等[4]观点具有一定的一致性。因此，所分析的砂岩岩心主要表现出3种应力敏感性特征，应力敏感性强的岩心更符合对数模型（Barre T和Barre P属于此类），中应力敏感岩心更适于乘幂模型（微裂缝花岗岩属于此类），弱应力敏感岩心更符合指数模型或者二项式模型。

图4　无因次渗透率与有效应力关系曲线

3　讨论

选择具强、中、弱3类应力敏感的岩心进行了激光共聚焦扫描实验[24]，建立岩心三维孔隙空间结构图（见图5，彩色（红色或者蓝色）部分代表孔隙），发现强应力敏感岩心（如D8-10、D23-8）中裂缝发育，符合对数模型的特征，且S值越大岩心中裂缝特征越显著；而弱应力敏感性岩心（MJ5515）的孔隙连通性好，裂缝不发育；中等应力敏感性岩心（如D15-2）的孔隙结构特征介于强和弱应力敏感性岩心之间——孔隙和裂缝共存。

图5　强、中、弱应力敏感性典型岩心三维孔隙空间分布

对比分析27块致密砂岩的铸体薄片也发现强应力敏感性岩心中裂缝发育（见图6a—6c），典型岩心S8、D8-12、D23-1中（微）裂缝较为发育；而弱应力敏感性岩心中孔隙发育（见图6d—6f），几乎不见裂缝，且孔隙连通性好，如D15-1、D47-6和MJ5515具有孔隙性岩石的特征，其S值与Jones等[4]测试的高渗透率岩石的S值一致，因此更适合用指数模型或者二项式模型表征。需要说明的是，尽管岩心MJ5515中发育粒缘缝和拉长状贴粒孔，但是该样品粒度较细（见表1），仍表现为孔隙性特征。此外，分析典型岩心的毛管压力曲线（见图7）发现，强应力敏感性岩心门槛压力较低、孔隙分选性差且偏向粗歪度（如岩心S8），孔隙具有裂缝性特征；弱应力敏感性岩心则表现为门槛压力较高、孔隙分选性好且偏向于细歪度（如岩心D15-1），岩石孔隙性特征显著。

图6　强、弱应力敏感性典型岩心铸体薄片照片

图7　典型岩心毛细管压力曲线、孔隙喉道分布曲线和渗透率贡献曲线

可见，是否发育裂缝是评价岩石应力敏感性强弱的关键因素。此外，岩石颗粒大小、黏土矿物类型和岩性也会影响储集层岩石的应力敏感性。

岩石骨架颗粒越大，岩石颗粒半径与孔隙孔径的差异将会越大，孔隙纵横比（见图1d）将越小，形成的“星形”孔隙裂缝特征越明显；再者，岩石骨架颗粒越大，岩石中将更容易形成较长的（微）裂缝（见图6和表1中巨砂岩S8和中砂岩D8-12），岩石的应力敏感性越强。在分析的27块砂岩中，粗砂和巨砂岩的应力敏感性普遍强于细砂岩的应力敏感性（见表1和图4），这与Dong等[8]观察到的细砂岩应力敏感性较小观点一致。

然而，部分粗砂岩或中砂岩却表现出弱应力敏感性特征（见表2），这些砂岩的显著特点是黏土矿物以高岭石为主，且岩石中不发育裂缝，高岭石晶间孔发育，孔隙连通性好（见图6d、6e），对应砂岩的渗透率与有效应力关系符合二项式模型或者指数模型。当这类粗砂岩或中砂岩中发育裂缝时，应力敏感性将增强（岩心DT1-8、D8-9、D66-3、D15-2和HH103-3呈中等应力敏感性，岩心D13-4呈强应力敏感性）。进一步分析发现，当中砂岩的黏土胶结物以混层矿物（如伊/蒙混层）为主且发育裂缝时（如D8-10和D8-12），岩心表现出强应力敏感特征，与黏土矿物以混层矿物或者伊利石为主的粗砂岩或者巨砂岩的应力敏感性特征相同，其渗透率与有效应力关系符合对数模型或者乘幂模型。这说明黏土矿物的类型影响岩石的应力敏感性，与David等[5]的观点一致，但与David等[5]的认识也有所差异，即胶结的黏土矿物类型不同，影响规律不一样，高岭石的存在会减弱应力敏感性，伊利石或混层矿物发育时岩石表现为更强的应力敏感性。

本文所分析的致密砂岩主要包括石英砂岩、岩屑石英砂岩、岩屑砂岩、长石岩屑砂岩、岩屑长石砂岩（见图8），与中国典型致密砂岩储集层的岩石类型基本一致[25]；其中石英砂岩和岩屑石英砂岩以粗砂和巨砂岩为主，岩屑砂岩包括巨砂、粗砂和中砂岩，岩屑长石砂岩为细砂岩，长石岩屑砂岩以细砂—极细砂为主（见表1）。石英砂岩、岩屑石英砂岩和岩屑砂岩的应力敏感性包括强、中、弱3种状态；而岩屑长石砂岩和长石岩屑砂岩可能是由于颗粒较小，主要表现为弱应力敏感性。为了使得所提出的应力敏感性划分标准更具有普适性，建议针对不同类型砂岩继续开展应力敏感性研究。

图8　致密砂岩样品岩性分布

4　结论

表征渗透率与有效应力关系的对数模型和二项式模型分别与裂缝模型和圆形管束模型（或者椭圆形管束模型）一致；乘幂模型和指数模型分别与裂缝模型和星形模型对应。

应力敏感系数S、α、β表达式中均含有岩石的微观结构参数，岩石本身的物理特性决定和影响其应力敏感性；3种应力敏感系数中，仅S中不含不确定指数n，具有明确的物理意义，适宜作为应力敏感性划分的参数：S >0.40为强应力敏感性；S<0.25为弱应力敏感性；0.25≤S≤0.40为中等应力敏感性。强应力敏感岩心更满足对数模型，弱应力敏感岩心更满足指数模型和二项式模型，中等应力敏感岩心满足乘幂模型。

裂缝发育与否是岩石应力敏感性强弱的关键因素；岩石骨架颗粒越大，岩石颗粒半径与孔隙孔径的差异将会越大，对应岩石的应力敏感性将会越强。

砂岩中黏土胶结物类型影响岩石的应力敏感性，高岭石胶结物的存在会减弱应力敏感性，发育伊利石或者混层矿物的岩石表现为更强的应力敏感性。

致谢：美国麻省理工学院Yves Bernabé在激光共聚焦扫描实验以及研究分析过程中提供了帮助,在此表示感谢！

符号注释：

a，b——椭圆管截面长半轴和短半轴，m；aref——参考应力σref下裂缝的半开度，m；c，d——星形管截面长半轴和短半轴，m；E——岩石弹性模量，MPa；Eeff——岩石有效弹性模量，MPa；h——裂缝面上微凸体分布高度均方根，m；K——渗透率，m2；K0——有效应力为0时的渗透率，m2；Kr——有效应力为20 MPa时的渗透率，m2；Kref——参考有效应力σref下的渗透率，m2；m，g，z——拟合系数；n——不确定指数；pc——围压，MPa；pp——孔隙流体压力，MPa；qx，qy——x方向和y方向上的流量，mL/s；r——圆形管束模型截面圆半径，m；R2——拟合相关系数；S——对数模型的应力敏感系数；α——乘幂模型的应力敏感系数；β——指数模型的应力敏感系数，MPa-1；ε——纵横比（椭圆形管中等于b/a 或星形管中等于d/c）；κ——有效应力系数；ν——泊松比；σre——有效应力，MPa；σref——参考有效应力，MPa。

参考文献：

[1] 贾承造, 邹才能, 李建忠, 等. 中国致密油评价标准、主要类型、基本特征及资源前景[J]. 石油学报, 2012, 33(3): 343-350.

JIA Chengzao, ZOU Caineng, LI Jianzhong, et al. Assessment criteria, main types, basic features and resource prospects of the tight oil in China[J]. Acta Petrolei Sinica, 2012, 33(3): 343-350.

[2] 邹才能, 翟光明, 张光亚, 等. 全球常规-非常规油气形成分布、资源潜力及趋势预测[J]. 石油勘探与开发, 2015, 42(1): 13-25.

ZOU Caineng, ZHAI Guangming, ZHANG Guangya, et al.Formation, distribution, potential and prediction of global conventional and unconventional hydrocarbon resources[J]. Petroleum Exploration and Development, 2015, 42(1): 13-25.

[3] 杨智, 侯连华, 陶士振, 等. 致密油与页岩油形成条件与“甜点区”评价[J]. 石油勘探与开发, 2015, 42(5): 555-566.

YANG Zhi, HOU Lianhua, TAO Shizhen, et al. Formation condition and “sweet spot” evaluation of tight oil and shale oil[J]. Petroleum Exploration and Development, 2015, 42(5): 555-566.

[4] JONES F O, OWENS W W. A laboratory study of low-permeability gas sands[J]. Journal of Petroleum Technology, 1980, 32(9): 1631-1640.

[5] DAVID C, WONG T F, ZHU W L, et al. Laboratory measurement of compaction-induced permeability change in porous rocks: Implications for the generation and maintenance of pore pressure excess in the crust[J]. Pure and Applied Geophysics, 1994, 143: 425-456.

[6] SIGAL R F. The pressure dependence of permeability[J]. Petrophysics, 2002, 43(2): 92-102.

[7] 李传亮. 储层岩石的应力敏感性评价方法[J]. 大庆石油地质与开发, 2006, 25(1): 40-42.

LI Chuanliang. Evaluation method for stress sensitivity of reservoir rock[J]. Petroleum Geology & Oilfield Development in Daqing, 2006, 25(1): 40-42.

[8] DONG J J, HSU J Y, WU W J, et al. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP hole-A[J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47(7): 1141-1157.

[9] 肖文联, 李闽, 赵金洲, 等. 低渗致密砂岩渗透率应力敏感性试验研究[J]. 岩土力学, 2010, 31(3): 775-779.

XIAO Wenlian, LI Min, ZHAO Jinzhou, et al. Laboratory study of stress sensitivity to permeability in tight sandstone[J]. Rock and Soil Mechanics, 2010, 31(3): 775-779.

[10] TERZAGHI K. Principles of soil mechanics[J]. Engineering News Record, 1925, 95(3): 874-878.

[11] BERNABLE Y. The effective pressure law for permeability in Chelmsford granite and Barre granite[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1986, 23(3): 267-275.

[12] ZHAO Jinzhou, XIAO Wenlian, LI Min, et al. The effective pressure law for permeability of clay-rich sandstones[J]. Petroleum Science, 2011, 8(2): 194-199.

[13] JONES F O. A laboratory study of effects of confining pressure on fracture flow and storage capacity in carbonate rocks[J]. Journal of Petroleum Technology, 1975, 27(1): 21-27.

[14] 尹尚先, 王尚旭. 不同尺度下岩层渗透性与地应力的关系及机理[J]. 中国科学: D辑: 地球科学, 2006, 36(5): 472-480.

YIN Shangxian, WANG Shangxu. The relationship and mechanism between permeability and formation stress under different scale[J]. SCIENCE CHINA Earth Sciences, 2006, 49(7): 714-723.

[15] WALSH J B. Effect of pore pressure and confining pressure on fracture permeability[J]. International Journal of Rock Mechanics and Mining Sciences, 1981, 18(5): 429-435.

[16] 国家能源局. SY/T 5358-2010 储层敏感性流动实验评价方法[S].北京: 石油工业出版社, 2010.

National Energy Administration. SY/T 5358-2010 Formation damage evaluation by flow test[S]. Beijing: Petroleum Industry Press, 2010.

[17] JAEGER J C, COOK N G W, ZIMMERMAN R W. Fundamentals of rock mechanics[M]. Malden, USA: Blackwell Publishing, 2007.

[18] SEEBYRGER D A, NURA A. A pore space model for rock permeability and bulk modulus[J]. Journal of Geophysical Research, 1984, 89(B1): 527-536.

[19] YALE D P. Network modeling of flow, storage, and deformation in porous rocks [D]. Stanford, California: Stanford University, 1984.

[20] 肖文联, 李闽, 赵金洲, 等. 非线性有效压力计算[J]. 地球物理学报, 2013, 56(8): 2808-2817.

XIAO Wenlian, LI Min, ZHAO Jinzhou, et al. Calculation of non-linear effective pressure[J]. Chinese Journal Geophysics, 2013, 56(8): 2808-2817.

[21] KRANZ R L, FRANKEL A D, ENGELDER T, et al. The permeability of whole and jointed Barre granite[J]. International Journal of Rock Mechanics and Mining Sciences, 1979, 16(4): 225-234.

[22] LI M, BERNABE Y, XIAO W L, et al. Effective pressure law for permeability of E-bei sandstones[J]. Journal of Geophysical Research, 2009, 114(B7): B07205.

[23] LI M, BERNABE Y, XIAO W L, et al. Nonlinear effective pressure law for permeability[J]. Journal of Geophysical Research, 2014, 119(1): 302-318.

[24] FREDRICH J T, MENENDEZ B, WONG T F. Imaging the pore structure of geomaterials[J]. Science, 1995, 268(5208): 276-279.

[25] 邹才能, 朱如凯, 吴松涛, 等. 常规与非常规油气聚集类型、特征、机理及展望: 以中国致密油和致密气为例[J]. 石油学报, 2012, 33(2): 173-187.

ZOU Caineng, ZHU Rukai, WU Songtao, et al. Types, characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations: Taking tight oil and tight gas in China as an instance[J]. Acta Petrolei Sinica, 2012, 33(2): 173-187.

联系作者：李闽（1962-），男，四川射洪人，硕士，西南石油大学教授，主要从事致密页岩油气渗流机理、油气田开发及测井解释研究及教学工作。地址：四川省成都市新都区新都大道8号，西南石油大学油气藏地质及开发工程国家重点实验室，邮政编码：610500。E-mail: hytlxf@126.com

（编辑张敏）

Evaluation of the stress sensitivity in tight reservoirs

XIAO Wenlian, LI Tao, LI Min, ZHAO Jinzhou, ZHENG Lingli, LI Ling
(State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China)

Abstract:The expressions of three types of stress sensitivity coefficients (S, α, β) are obtained on the basis of analysis of the empirical models and theoretical models on the relationships between permeability and effective stress, and the stress sensitivity evaluation standard is proposed considering experiment data and rock micro-structural features. Then the empirical models and theoretical models were used to fit experiment data of low-permeability and tight sandstones and different types of granites, which promotes the understanding of the empirical models and the physical meanings of the stress sensitivity coefficients. According to the study of the three types of stress sensitivity coefficients and the relationship of effective stress and permeability, it is found that the stress sensitive coefficient S was suitable for evaluating the stress sensitivity (strong stress sensitivity: S>0.40; low stress sensitivity: S<0.25; medium stress sensitivity: 0.25≤S≤0.4). Meanwhile, it is also found that strong-stress-sensitivity cores are more suitable to be characterized by the logarithmic model, while the exponential model (or binomial model) occurred more frequently in low-stress-sensitivity cores, and medium-stress-sensitivity cores are more likely to be described with the power model. Finally, the evaluation standard is discussed based on the micro-structure in the low-permeability and tight sandstones. The results show that the crack-like pores in the strong-stress-sensitivity cores are obvious, but low-stress-sensitivity cores have the characteristics of porous rocks; moreover, the types of cemented clay minerals, the size of rock grain and lithology have impact on stress sensitivity.

Key words:tight sandstone; stress sensitivity; stress sensitivity coefficient; effective stress; permeability; micro-structure

基金项目：国家自然科学基金项目“鲕粒灰岩渗透率非线性有效应力研究”（41404083）和“充填粘土裂缝砂岩N-ESLK理论与实验研究”（51274169）；国家重点基础研究发展计划（973）项目“陆相致密油高效开发基础研究”（2015CB250900）

中图分类号：TE348

文献标识码：A

文章编号：1000-0747(2016)01-0107-08

DOI:10.11698/PED.2016.01.13

第一作者简介：肖文联（1983-），男，四川渠县人，博士，西南石油大学讲师，主要从事岩石渗流物理及油气田开发方面的教学与研究工作。地址：四川省成都市新都区新都大道8号，西南石油大学油气藏地质及开发工程国家重点实验室，邮政编码：610500。E-mail: joshxiao@163.com

收稿日期：2015-06-24修回日期：2015-09-20