钻孔作业中反向扩孔气动冲击器尾气携岩特性

徐海良，李旺，赵宏强，徐绍军（中南大学机电工程学院）

钻孔作业中反向扩孔气动冲击器尾气携岩特性

徐海良，李旺，赵宏强，徐绍军
（中南大学机电工程学院）

摘要：建立了由反向扩孔气动冲击器排气孔到后封头的排屑流场，运用计算流体力学理论和FLUENT仿真软件研究了冲击器工作过程中尾气的携岩特性。基于冲击器的结构和工作原理，对气固两相排屑流场进行了数值仿真模拟，进而得到流场的气相特性以及岩屑颗粒运动轨迹和浓度分布规律。结果表明：冲击器排气孔尾气进入排屑流场后流速降低，流场压力由入口到出口逐渐降低；岩屑颗粒向流场底部聚集，颗粒平均浓度沿着远离入口方向变化不大，最大浓度沿着远离入口方向逐渐下降，最终趋于平稳。分析了钻进速度和尾气流量对携岩特性的影响，结果表明：随着钻进速度的增加尾气携岩能力下降，额定工作压力0.8 MPa时钻进速度应小于12.6 m/h；随着尾气质量流量的增加携岩能力提高，施工时应该在保证冲击器工作性能的情况下适当增加尾气质量流量。图12表1参13

关键词：气体钻井；反向扩孔；气动冲击器；排屑流场模型；携岩特性；气固两相流；数值模拟

0　引言

非开挖技术[1]是一种利用岩土钻掘设备进行地下管道铺设和修复的施工技术，应用该技术能够在不进行地表开挖的情况下实现管道的铺设，减少了施工时对交通、环境和建筑的破坏。非开挖施工时，针对岩石、砾卵石复杂地层中的钻掘扩孔作业设计了一种新型气动冲击设备——反向扩孔气动冲击器[2]。该设备利用空气压缩机提供的高压气流，经过内部复杂气路结构推动活塞高速周期运动，运动中活塞撞击冲击器的钻头实现扩孔作业，与传统扩孔设备相比能够极大地提高开挖岩石、砾卵石等复杂地层的施工效率[3]。冲击器尾气的携岩能力，不仅关系到岩屑颗粒能否顺利排到孔外，还关系到冲击器的整体性能。本文运用气固两相流体力学、固体颗粒物料气力输送理论，借助计算流体力学仿真软件FLUENT[4]对钻头产生的岩屑在冲击器与岩石孔壁之间环形间隙中的流动规律进行理论分析，研究此段气路的气体流动规律和岩屑的运动特性，分析钻进速度和尾气流量对携岩能力的影响。本文研究问题与气体钻井水平井段携岩问题从本质上有许多相似之处，可供参考。

1　反向扩孔气动冲击器排屑流场模型

反向扩孔气动冲击器由钻头、进气杆、活塞、活塞阀、活塞缸和后封头组成（见图1），冲击器扩孔直径为190 mm，气缸直径160 mm，冲击器长度1 500 mm。图1中冲击器钻头上3个均匀分布的排气孔直径为22 mm。空气压缩机提供的高压气体在推动冲击器工作周期完成后，由排气腔通过排气孔进入到冲击器的排屑流场。气流由排气孔进入钻头表面与岩石壁面形成的气腔中，在岩石壁面的阻挡下，气流从钻头上的开槽和钻头与孔壁的间隙反向进入冲击器与孔壁形成的环形排屑通道中，经过环形通道流出此段岩屑通路。钻头表面与岩石壁面间距离为10 mm（钻齿高度），流场外径190 mm，内径160 mm。冲击器的排屑流场较复杂，采用结构网格和非结构网格相结合的方式，对其进行网格划分。冲击器气缸外表面与孔壁形成的环形间隙段采用正六面体单元的结构网格划分，使其计算精度高且计算成本较低[5-6]；由于排气孔以及钻头表面与岩石壁面间气腔部分形状较复杂，采用四面体单元的非结构网格划分[5-6]。

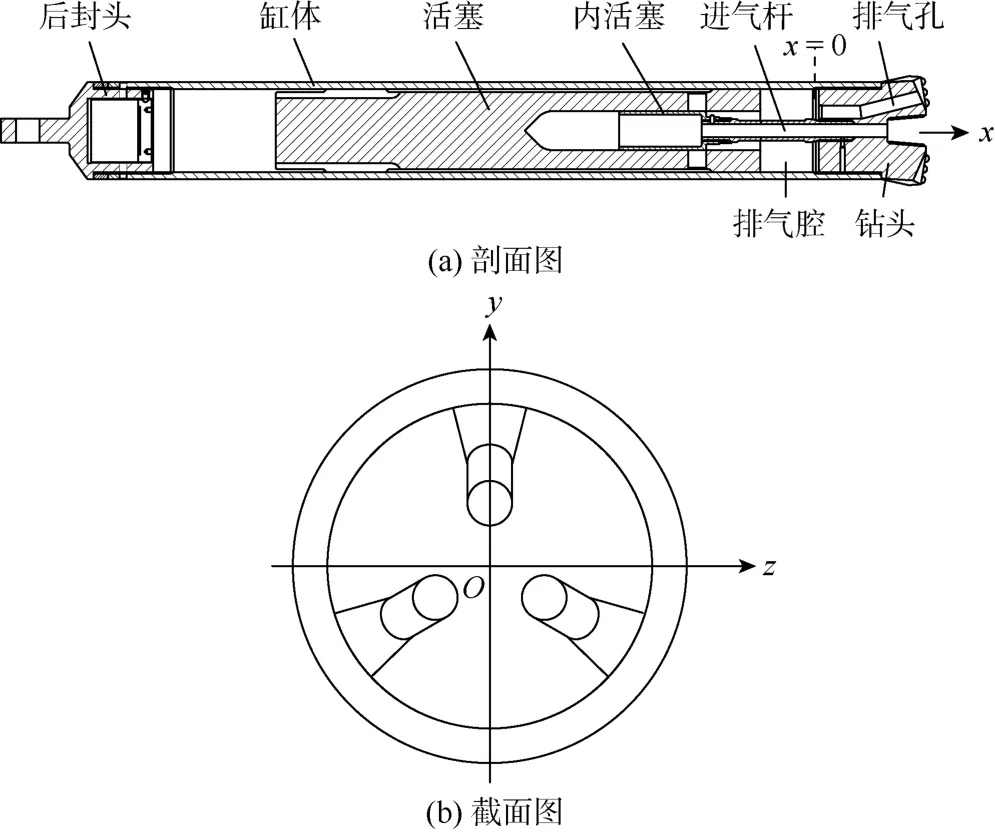
图1　反向扩孔气动冲击器结构示意图

2　数学模型

岩石、砾卵石地层较复杂，冲击器钻进速度较慢。钻头直径为190 mm，取钻进速度为4.2 m/h，岩石密度为2 400 kg/m3，则钻进时产生的岩屑质量流量为0.08 kg/s，冲击器排气孔尾气质量流量为0.02 kg/s。由此可以得到流场中固相与气相体积比远小于10%。岩屑颗粒间相互影响较小，不考虑颗粒间相互作用[7]，采用欧拉-拉格朗日法对其流场进行数值模拟[8]，将岩屑颗粒看成离散相，在拉格朗日坐标系下进行求解。

岩屑颗粒在流场中受到压差阻力、摩擦阻力、Basset力（两相流中颗粒与流体存在相对加速度时所产生的一种非恒定气动力）、压强梯度力、速度梯度力、惯性力和重力等的影响。其中，压差阻力影响最大，当颗粒粒径较大时受重力的影响明显，其他作用力对颗粒的运动影响较小，可以不考虑。

针对冲击器排屑流场气固两相流动建立数学模型，模型的控制方程主要包括连续性方程、动量守恒方程和能量守恒方程[9]。

连续性方程为：

动量方程为：

能量方程为：

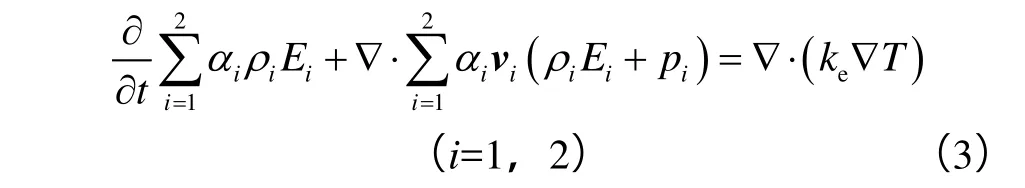
扩孔冲击器排屑流场为气固两相湍流流动[10]，复杂的三维湍流数值计算问题如果采用直接求解对计算机性能要求较高，工程实际中通常通过近似和简化来降低运算难度，本文利用RNG k-ε湍流模型[11]进行求解：

模拟时气相为空气，其密度为1.225 kg/m3，运动黏度为1.78×10-5Pa·s。空气从冲击器的排气孔进入流场，采用质量流量入口边界，质量流量为0.02 kg/s，入口最大静压为0.22 MPa，出口边界为压力边界，压力值为0.10 MPa。岩屑颗粒在孔底岩石壁面释放，其质量流量为0.08 kg/s。取颗粒粒径为5 mm，初始速度为零。

3　数值模拟结果及讨论

3.1气相特性

图2为反向扩孔气动冲击器底部排屑流场气相特性图，可以看出：气流在冲击器排气孔时，排气孔内气流速度逐渐增加，气压逐步降低；排气孔中的高速射流进入孔底时，由于岩壁的阻挡，气流速度迅速降低，气压升高，在孔底岩石壁面形成3个明显的高压漩涡区；在岩壁的阻挡下射流方向改变，由冲击器排气孔进入环形排屑通道，在转弯处形成低压漩涡；气流进入环形通道后由于出口压力低于入口压力定值，以及存在壁面摩擦，环形通道内压力逐渐降低，最终达到和出口压力一样的常值。

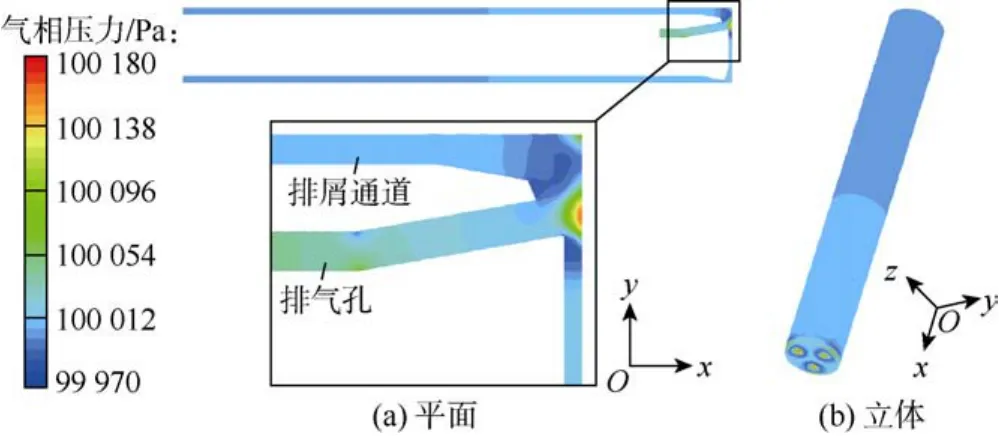
图2　排屑流场气相压力云图

图3为反向扩孔气动冲击器排屑流场纵向截面速度云图，可以看出：气流由冲击器排气孔进入钻头与岩壁形成的气腔内，由于岩壁的阻挡气流反向进入环形排屑通道，最终进入出口；排气孔内的气流速度沿其轴线方向逐渐增加到15 m/s，气流进入排气孔出口时由于气腔空间急剧增加，气流速度迅速下降到5 m/s，并且在排气孔两侧形成气流漩涡；进入到环形通道后气流速度方向改变，由于通道壁面的摩擦阻力，流速逐渐降低，最终接近2 m/s。

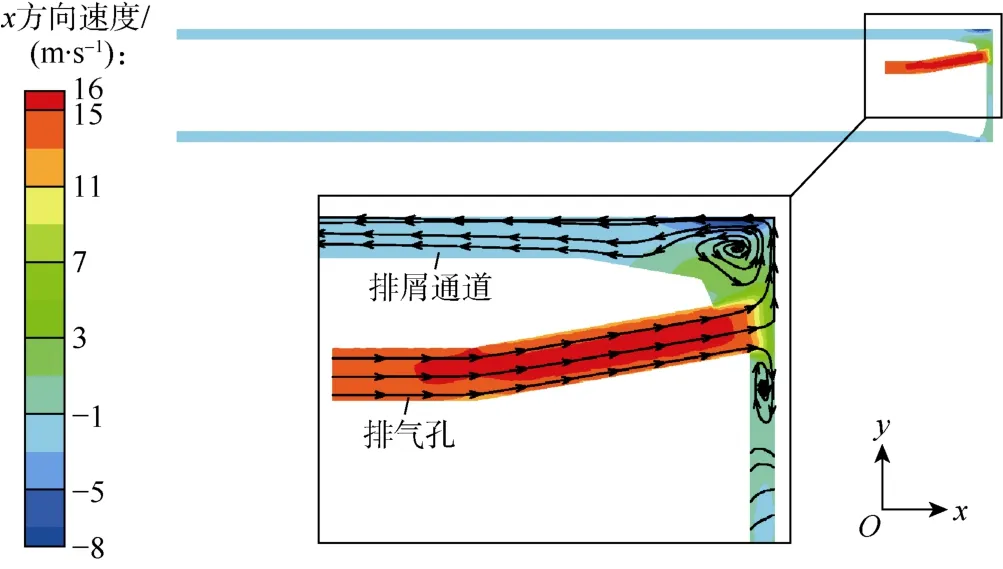
图3　流场速度云图

3.2携岩特性

3.2.1岩屑颗粒浓度分布规律

通过仿真模拟可以得到环形岩屑通道沿x轴方向不同位置处截面岩屑浓度分布云图（见图4）。由图4可知，岩屑颗粒主要集中在管路底部，随着x值的减小，浓度逐渐减小，最终达到稳定的排屑浓度值；x=170 mm处截面处于钻头表面和岩石壁面之间，冲击器排气孔高压气体带动下，岩屑由岩石壁面向空腔中扩散，在岩石与钻头之间形成浓度较高而分布范围广泛的气固混合物，受重力的影响岩屑颗粒浓度出现分层，越靠近底部颗粒浓度越高（达到160 kg/m3），而顶部颗粒浓度几乎为零，岩屑在环形通路底部形成岩屑床；钻头表面与岩石壁面之间的颗粒大部分会沉积在两者之间的空腔，未能在气流的作用下输运出去，在钻头的冲击和旋转钻进作用下进一步粉碎；x=100 mm处的岩屑已经进入冲击器排屑的输运管路，此时浓度较低，底部最高浓度在120～130 kg/m3；随着x值的减小浓度进一步降低，当达到出口时环形管路截面最大岩屑浓度降低到60～70 kg/m3。

图4　x轴方向不同位置处截面的岩屑颗粒浓度分布云图

图5为沿x轴方向不同截面处岩屑颗粒平均浓度和最大浓度分布曲线，可以看出：颗粒平均浓度沿着远离入口方向变化不大，这是因为钻进速度不变，进入流场的颗粒质量流量不变，只有少许颗粒在运动中无法逃逸出出口，因此平均浓度基本不变；最大浓度沿着远离入口方向逐渐下降，最终趋于平稳，在x=100 mm处最大浓度为123.9 kg/m3，颗粒运动到出口时截面最大浓度下降为67.9 kg/m3，主要是由于随着颗粒远离入射面，颗粒在流场中分布逐渐均匀，最终随着颗粒运动达到稳定值，但是重力的影响使得颗粒在流场底部聚集，使得最大浓度远大于平均浓度。

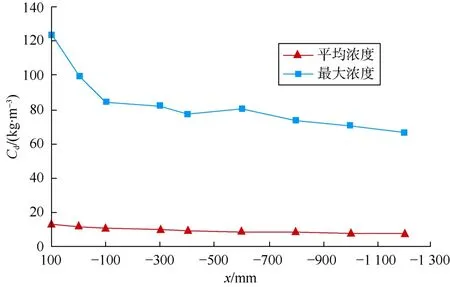
图5　x轴方向不同位置处截面岩屑浓度分布曲线

图6为沿x轴方向不同截面下半边圆周上的颗粒浓度沿z轴方向的分布情况，可以看出：x值越小的截面，颗粒浓度越小；不同截面处岩屑浓度沿z轴方向的分布趋势相同：由z=-100 mm到z=0，颗粒浓度逐渐增加，z=0时达到最大值，然后由z=0到z=100 mm，颗粒浓度逐渐减小到零。这是由于岩屑颗粒由排气孔向出口处运动的过程受到重力的影响，几乎全部颗粒堆积在管路底部，造成了浓度分布不均匀。

图6　x轴方向不同位置处截面岩屑浓度沿圆周的分布曲线

3.2.2岩屑颗粒运动轨迹和运动规律

岩石被冲击器钻头破碎后由岩石壁面释放，进入钻头表面与岩石壁面形成的气腔内。在气腔内的高压气流作用下，岩屑以较快的速度随气流运动，快速运动的岩屑与钻头和岩石壁面发生碰撞导致岩屑无规则运动，只有当颗粒运动到环形通道入口时才能从气腔逃逸出去，这就导致了该区域内岩屑颗粒的富集（见图7）。逃逸出气腔的岩屑进入环形通道后运动较规则，颗粒轨迹明显，由于气压和气流速度的降低，环形管路中岩屑运动的速度也下降，运动过程中碰到环形通道壁面时会反弹，形成S状轨迹。同时管路底部出现不均匀的疏密流，管底岩屑颗粒跳跃前进，管路上部的颗粒还是处于悬浮前进状态。

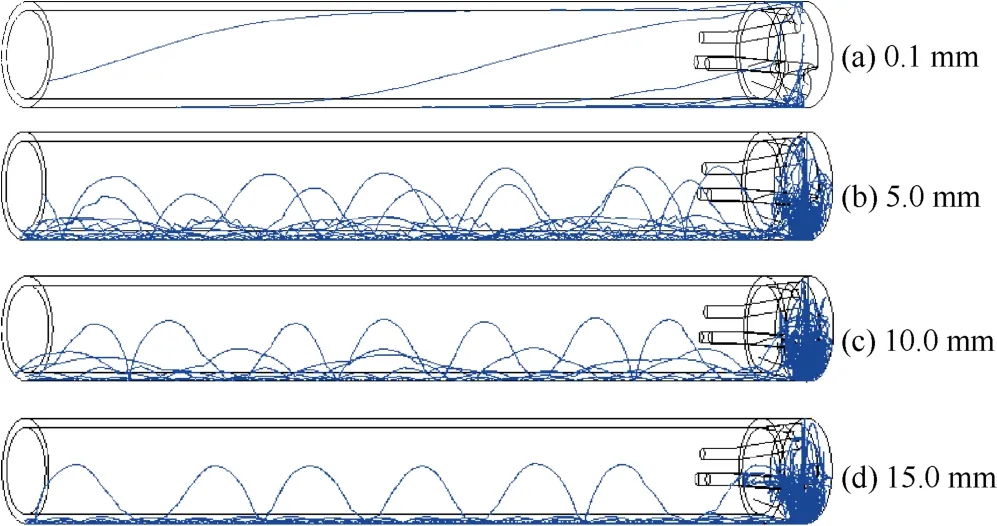
图7　不同粒径岩屑颗粒的运动轨迹

在输入气相质量流量为0.02 kg/s的情况下，为了研究不同直径岩屑颗粒运动特性，分别选取了粒径为0.1 mm、5.0 mm、10.0 mm、15.0 mm的4组颗粒，每组11个颗粒均匀分布在z=0处截面与岩石壁面的交线上，得到如图7所示的颗粒运动轨迹图。当颗粒直径为0.1 mm时，由于运动过程受到的重力影响较小，在气流的作用下，轨迹流畅，分布均匀，颗粒为均匀流。随着颗粒直径的增加，重力对轨迹影响明显，颗粒向环形通道底部集中，岩屑颗粒跳跃前进。当颗粒直径达到15 mm时，只有少量表面颗粒悬浮前进，剩余颗粒在环形通道底部，形成砂丘流[12-13]。表1为4种粒径颗粒在环形通道中的逃逸情况。综合考虑，在输运过程中岩屑颗粒粒径尽量控制在5～10 mm比较合适。

表1　不同粒径颗粒逃逸情况

图8为不同粒径岩屑颗粒运动速度随时间变化曲线，可以看出：粒径为0.1 mm时，颗粒在通道内停留的时间较短，且运动速度较小（接近1 m/s），颗粒受到的重力影响小，随着气流运动，与通道碰撞次数少；随着粒径的增加，颗粒停留时间增加且运动速度保持在2 m/s左右。

3.3钻进速度对携岩特性的影响

气动冲击器钻进过程中产生的岩屑会随着钻进速度的增加而增多，可以根据环形通道出口处的截面岩屑浓度分布图，分析不同钻进速度时的携岩能力。

当入口气相流量为0.02 kg/s时，由图9可知：随着钻进速度的增加，携岩能力下降；当钻进速度在12.6 m/h时，岩屑床形成，并且只占据环形通路底部一小部分；钻进速度由12.6 m/h增加到21.0 m/h时，岩屑浓度增加更快，岩屑床高度迅速增高，当钻进速度为21.0 m/h时，岩屑床高度达到环形通路总高度的1/4；钻进速度达到37.8 m/h时，岩屑床高度达到环形通路总高度的1/3。因此，反向扩孔气动冲击器破岩钻进速度应该小于12.6 m/h，当钻进速度大于此速度时，环形通路的携岩能力将逐渐下降，冲击器将会出现堵死现象。

图8　不同粒径岩屑颗粒运动速度随时间变化曲线

图9　不同钻进速度时环形通道出口截面颗粒浓度分布云图

图10为不同钻进速度时环形通道出口处的截面平均浓度和最大浓度曲线图，可以看出：随着钻进速度的增加，出口截面浓度最大值急剧增加，由钻进速度为2.1 m/h时的33.90 kg/m3增大到钻进速度为37.8 m/h时的562.58 kg/m3；出口截面的平均浓度增长较慢，由3.76 kg/m3增加到62.47 kg/m3。

3.4入口气相流量对携岩特性的影响

图11为不同入口气相质量流量时（钻进速度4.2 m/h）出口处的岩屑浓度分布云图，可以看出：随着气相质量流量的增加，环路携岩能力提高；当入口气相流量为0.02 kg/s时，颗粒在环路底部聚集，形成岩屑床；气相流量增加到0.03 kg/s时，通路底部聚集岩屑减少；气相流量由0.04 kg/s增加到0.06 kg/s时，岩屑在环路中分布逐渐均匀。增大排屑流场气相质量流量，需要改变冲击器的结构参数或系统参数，进而影响冲击器的综合性能。因此，气相质量流量的选择，应该综合考虑携岩能力和冲击器的工作效率。

图10　不同钻进速度时环形通道出口截面浓度分布曲线

图11　不同入口气相流量下出口截面颗粒浓度云图

图12为不同气相流量下出口截面颗粒平均浓度和最大浓度变化曲线，可以看出：随着入口气相流量的增加出口截面最大浓度先迅速下降，后下降速度减缓；由于钻进速度不变，进入排屑通路的岩屑质量流量不变，所以岩屑平均浓度变化趋势不明显。

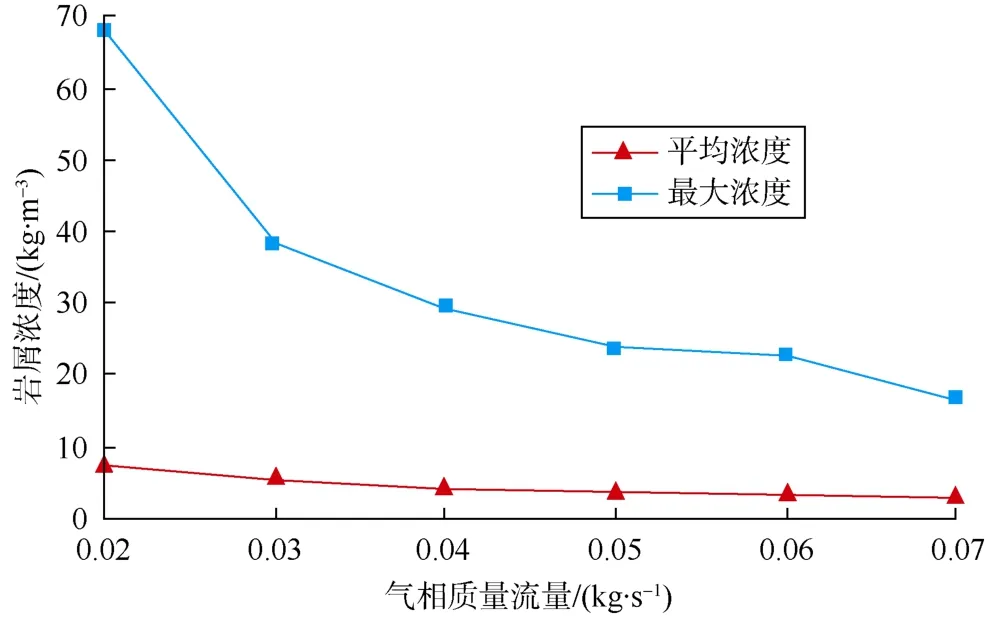
图12　不同入口气相流量下出口截面颗粒浓度曲线

4　结论

反向扩孔气动冲击器钻进过程中，气流由冲击器排气孔进入钻头与岩壁形成的气腔内，由于岩壁的阻挡气流反向进入环形排屑通道，冲击器钻进速度为4.2 m/h条件下，冲击器排气孔尾气以接近15 m/s的速度进入排屑流场，达到出口时气体流速下降到2 m/s。流场压力由入口到出口呈梯度分布且逐渐降低。

排屑流场中，由于重力的作用岩屑颗粒向流场底部聚集，导致截面颗粒浓度分布不均匀。截面上半圆周浓度为零，下半圆周浓度越靠近底部越高，出口处截面底部最大浓度达到67.9 kg/m3。沿x轴方向不同截面颗粒平均浓度基本不变，最大浓度由123.9 kg/m3下降到67.9 kg/m3。

随着钻进速度的增加环路携岩能力下降，额定工作压力0.8 MPa时，破岩钻进速度应该小于12.6 m/h，才能保证尾气的携岩能力。随着入口气相质量流量的增加，环路携岩能力提高，施工时应该在保证冲击器工作性能的情况下适当增加尾气质量流量。

符号注释：

C1，C2——经验常数；Cd——岩屑浓度，kg/m3；dj——第j个方向的位移，m；F——体积力矢量，N/m3；g——重力加速度矢量，m/s2；Gb——浮力产生的湍流动能，kg/ （m·s3）；Gk——层流速度梯度产生的湍流动能，kg/（m·s3）；i——第1，2相（即气相、固相）；j——第1，2，3个方向（即x，y，z方向）的方程；k——湍流动能，m2/s2；ke——有效热传导率，W/（m·K）；p——压力，Pa；pi——第i相面应力，Pa；t——时间，s；T——温度，K；uj——第j个方向流体速度，m/s；vi——第i相平均速度矢量，m/s；vm——气固两相平均混合速度矢量，m/s；x，y，z——直角坐标系；ia——第i相体积分数，%；ka，ea——湍流普朗特常数；ε——湍流耗散率，m2/s3；μ——流体黏度，Pa·s；μe——流体有效黏度，Pa·s；μm——气固两相混合黏度，Pa·s；μt——湍流黏度，Pa·s；ρ——流体密度，kg/m3；ρi——第i相密度，kg/m3；ρm——气固两相混合密度，kg/m3。

参考文献：

[1] 侯树刚, 陈静. 非开挖技术的发展研究[J]. 科技进步与对策, 2003(S1): 232-233.

HOU Shugang, CHEN Jing. Development of trenchless technology[J]. Science & Technology Progress and Policy, 2003(S1): 232-233.

[2] 徐绍军, 徐大鹏, 徐海良, 等. 气动回扩锤的计算机仿真与优化研究[J]. 工程机械, 2008(1): 16-19.

XU Shaojun, XU Dapeng, XU Hailiang, et al. Computer simulation and optimazation of pneumatic back reamer[J]. Construction Machinery and Equipment, 2008(1): 16-19.

[3] MALARD F, DATRY T, GIBERT J. Subsurface sediment contamination during borehole drilling with an air-actuated down-hole hammer[J]. Journal of Contaminant Hydrology, 2005, 79(3): 156-164.

[4] 韩占忠, 王敬, 兰小平. FLUENT流体工程仿真计算[M]. 北京:北京理工大学出版社, 2004.

HAN Zhanzhong, WANG Jing, LAN Xiaoping. Engineering simulation and calculation of fuild by FLUENT[M]. Beijing: Beijing Institute of Technology Press, 2004.

[5] 张涛, 李红文. 管道复杂流场气固两相流DPM仿真模型优化[J].天津大学学报(自然科学与工程技术版), 2015, 48(1): 39-48.

ZHANG Tao, LI Hongwen. Simulation optimazation of DPM on gas-solid two-phase flow in complex pipeline flow filed[J]. Journal of Tianjin University(Science and Technology), 2015, 48(1): 39-48.

[6] WANG K, PAN H, LIU Z. Numerical simulation on dense phase pneumatic conveying diversion characteristics in branch pipeline[J]. Journal of University of Jinan, 2013, 27(3): 303-308.

[7] 柳贡慧, 宋廷远, 李军. 气体钻水平井气体携岩能力分析[J]. 石油钻探技术, 2009, 37(5): 26-29.

LIU Gonghui, SONG Tingyuan, LI Jun. Analysis on cutting carrying capacity of gas in gas drilling for horizontal well[J]. Petroleum Drilling Techniques, 2009, 37(5): 26-29.

[8] HUBER N, SOMMERFELD M. Modelling and numerical calculation of dilute-phase pneumatic conveying in pipe systems[J]. Powder Technology, 1998, 99(98): 90-101.

[9] 周方奇, 施安峰, 王晓宏. 压裂油藏导流裂缝多相流动的高效有限差分模型[J]. 石油勘探与开发, 2014, 41(2): 239-243.

ZHOU Fangqi, SHI Anfeng, WANG Xiaohong. An efficient finite difference model for multiphase flow in fractured reservoirs[J]. Petroleum Exploration and Development, 2014, 41(2): 239-243.

[10] 郭建华. 气体钻井环空气固两相流动数值模拟研究[D]. 成都: 西南石油大学, 2006.

GUO Jianhua. Numerical simulation of annular gas-solid two-phase flow in gas drilling[D]. Chengdu: Southwest Petroleum University, 2006.

[11] YAKHOT V, ORSZAG S A. Renormalization group analysis of turbulence: I, Basic theory[J]. Journal of Scientific Computing, 1986, 1(1): 3-51.

[12] FAN Chun. Plug flow dense phase pneumatic conveying[J]. Advances in Mechanics, 2002, 32(4): 599-612.

[13] SAVAGE S B. Analyses of slow high-concentration flows of granular materials[J]. Journal of Fluid Mechanics, 1998, 377: 1-26.

（编辑胡苇玮）

Cuttings carrying characteristics of back-reaming pneumatic impactor exhaust during drilling operation

XU Hailiang, LI Wang, ZHAO Hongqiang, XU Shaojun
(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract:The flow fields of chip removal from the impactor’s exhaust hole to its rear head were established to study the cuttings carrying characteristics of back-reaming pneumatic impactor exhaust by utilizing the computational fluid dynamics theory and simulation software Fluent. Based on the structure and working principle of the impactor, the gas solid two phase flow was simulated, and the gas phase characteristics of the flow field and the moving trajectory and concentration distribution of particles were obtained. The research shows that: once the exhaust enters the field its speed will slow down and the field pressure will gradually decrease from the entrance to the exit; cuttings particles will gather around the bottom and there is minor variation in their average concentration as they are distributed along a contrary direction against the entrance while the maximum concentration descends along the same direction and finally becomes stable. Moreover, the effect of drilling speed and exhaust mass flow of the impactor on the solid carrying characteristics was analyzed. The result demonstrates that: as the drilling speed increases, the carrying ability of exhaust decreases and when the rated operation pressure is 0.8 MPa, the drilling speed should be less than 12.6 m/h; as the mass flow rate of exhaust increases, the carrying ability increases as well, and the mass flow rate should be moderately increased under the condition of ensuring the working performance of the impactor.

Key words:gas drilling; back-reaming; pneumatic impactor; cuttings flow field model; cuttings carrying characteristics; gas-solid two-phase flow; numerical simulation

基金项目：国家自然科学基金（51375499）

中图分类号：TH47

文献标识码：A

文章编号：1000-0747(2016)01-0121-06

DOI:10.11698/PED.2016.01.15

第一作者简介：徐海良（1965-），男，湖南湘乡人，博士，中南大学机电工程学院教授，主要从事海洋采矿和矿山机械等方面的教学和研究工作。地址：湖南省长沙市岳麓区中南大学机电工程学院D315，邮政编码：410083。E-mail：134250@csu.edu.cn

收稿日期：2015-03-24修回日期：2015-11-28