厚金属板与任意方位圆柱线圈间的电磁力计算

罗垚

(武汉大学 电气工程学院，湖北 武汉 430072)



厚金属板与任意方位圆柱线圈间的电磁力计算

罗垚

(武汉大学 电气工程学院，湖北 武汉 430072)

摘要:针对一个交流电激励的圆柱线圈倾斜放置于金属板上方时，它们之间的电磁作用力无法以传统方法进行解析计算的问题，引入高阶矢量势求解该问题，并采用矢量分析和Struve函数化简，可得到适用于任意方位圆柱线圈的二重积分表达式。所得结果表明任意方位圆柱线圈至多受到两个方向力的作用。在线圈轴垂直或平行于导电板的特殊情形，表达式可进一步简化为单重积分，而线圈将只受垂直力的作用。随后以数值算例对给出公式的有效性进行验证。数值结果表明，对于线圈轴的某个倾角，垂直力分量周期均值可以为零，而水平力分量周期均值将在某个倾角处达到最大值。当线圈通以直流电时，仅当金属板的磁导率与空气磁导率一致时线圈才不受电磁力的作用。

关键词:圆柱线圈；电磁力；高阶矢量势；Bessel函数；Struve函数

0引言

当一个置于平板导体附近的矩形截面圆柱线圈通以交变电流时，由于线圈的交变电磁场将在导体中感应出涡流，线圈本身将受到这一涡流的电磁力作用。这样的电磁结构在电工技术中有许多应用，如快速动作断路器(fast acting circuit breaker,FACB)[1]。对这种结构的电磁作用力的计算，常见于线圈轴线与导电体表面垂直的情形[1-3]。若线圈轴线倾斜于导电体表面，则此时的电磁力分析传统上只能借助于纯数值方法，如有限元法(FEM)，边界元法(BEM)。然而，考虑到纯数值方法无法给出待求电磁力与电磁系统各结构参数之间的函数关系，故在这一问题中解析或半解析工作仍然具有不可取代的优势。在已有工作中，为了便于计算通常将磁通密度B表为磁矢势A的旋度，但这一方法却无法用以处理线圈轴与导电面不垂直的一般情形。为了对一般方位的线圈电磁力进行解析处理，我们将引入高阶矢量势并借助Fourier积分求得一般情形的电磁力表达式。所得的电磁力表达式包括3个函数，它们均含二重积分，在线圈轴垂直于导电面的特殊情形可化为单重积分表达式。

1导电板附近任意载流环的电磁力作用

设有电导率κ，磁导率μ=μrμ0(μ0=4π×10-7H/m)的无穷大金属板，其厚度较之趋肤深度而言可视为无穷大，即可将该金属板视为一半无穷导电空间。在其上方的非导电空间磁导率为μ0，有一任意方位和形状的载流环c置于其中，而环c上载有电流i=Icosωt。由于i随时间变化，故其将在下方的导电板中感应出涡流，而环c本身则将受到这一涡流在上半空间激发出的磁场的电磁力作用。传统的势论仅能处理载流环为水平的情形而无法对任意方位的载流环进行解析计算。然而，若考虑Coulomb规范

divA=0,

(1)

则可对A可引入高阶矢势P[4]

A=rotP,

(2)

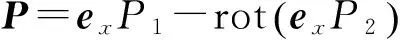
(3)

其中：P1，P2为两个仅与坐标有关的标量函数，ex为x方向的单位矢量。由此可以Fourier积分求得导电板中的感应电流在上半空间中激发的磁矢势

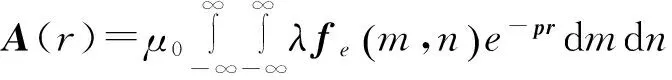
(4)

其中

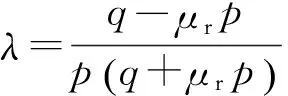
(5)

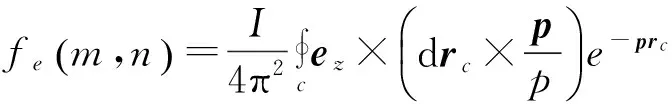
(6)

式(4)由Biot-Savart定律得出，故对环c的方位与形状均无限制。另由式(4)，式(6)的形状可以看出，无论载流环的形状与方位如何，由导电板中感应电流在上半空间激发的磁矢势均不含垂直分量。

得到磁矢势A后即由B=rotA得到感应磁通密度。由Ampere定律得到随时间变化的微分力为

dF(t)=I(t)drc×B(t)。

(7)

其中B(t)为导电板中感应电流在上半空间激发的磁感应强度。对于时谐激励源，我们关心的通常是一个周期内的平均力

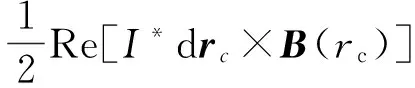
(8)

其中*表示复共轭量。从而载流环在一个周期内所受的平均力将为

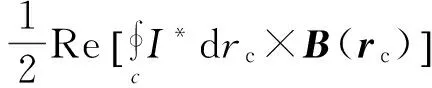
(9)

2任意方位矩形截面圆柱线圈感应场的确定

设上半非导电空间中有一载流圆环圆心为A，半径为R，圆环轴线为l，所载电流为i=Icosωt。若取过点A且垂直于导电平面的直线为z轴，将l在z=0上的投影取为y轴，并设l与z=0交于点B，则可设OA=H，AB=a，并记AB与z轴的夹角为γ，如图1所示。在这样的坐标选择下，我们得到源点矢量为

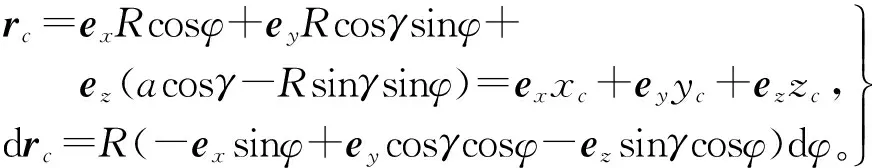
(10)

运用积分

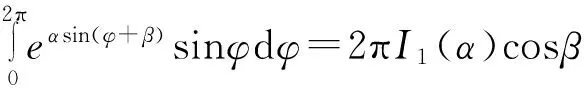
(11)

(12)

其中I1(α)为第一类一阶变形Bessel函数，我们得到矢量激励普函数为

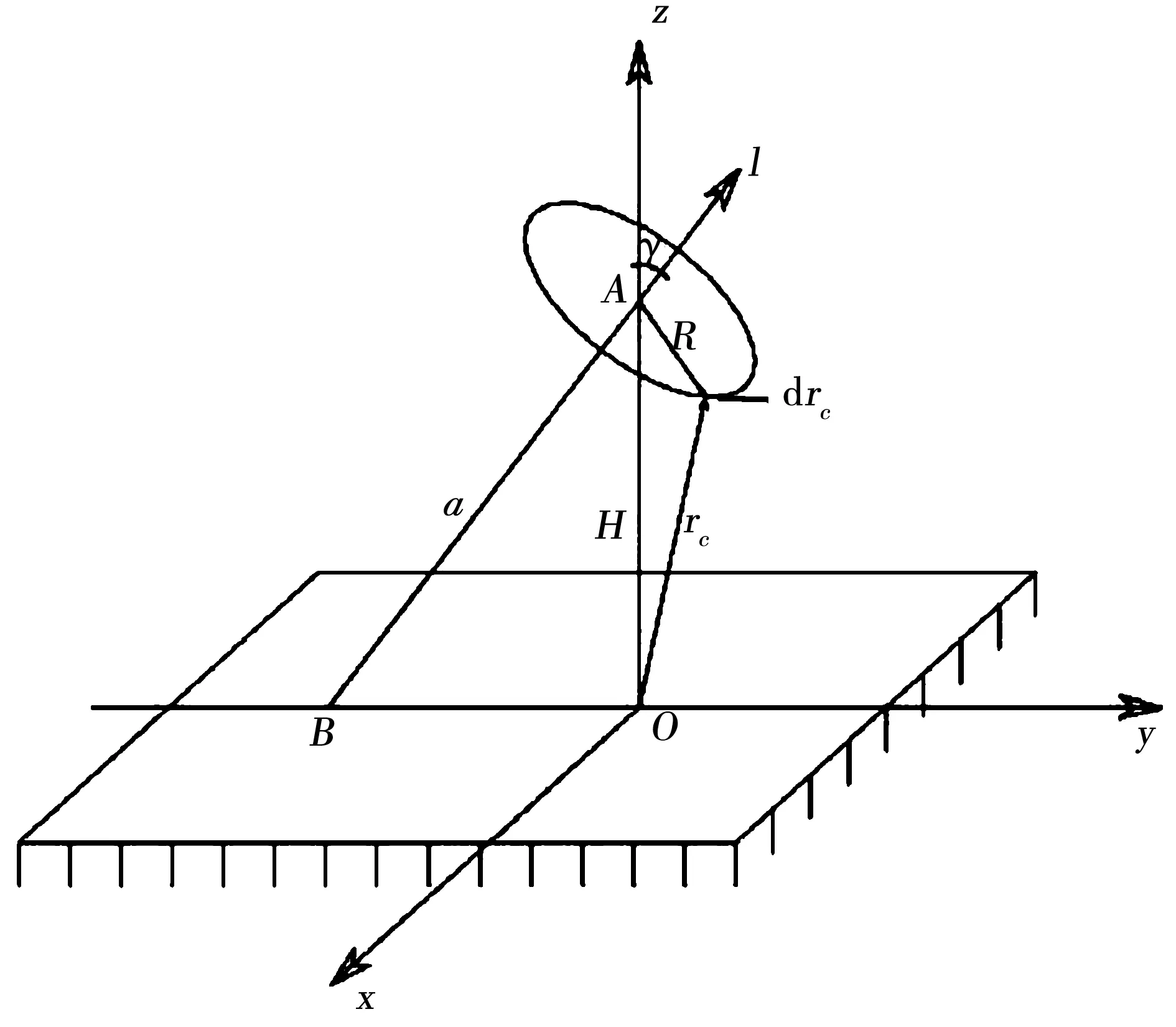
图1　任意位置圆环的坐标系选取Fig.1　　　　Selection of coordinate system for arbitrarily　　　 located circular loop

(13)

其中

u=nsinγ-jpcosγ。

(14)

从而

(-exn+eym)dmdn。

(15)

矩形截面圆柱线圈的感应场可由对单个载流圆环的感应场进行积分得到。设有一导电半无穷空间上方的圆柱线圈，其匝数为N，内外半径分别为R1，R2，高为2h，坐标系取法如图1，这时线圈轴与z轴夹角为γ，线圈中心点A与坐标原点间的距离为H，AB=d。将式(15)对轴向与径向积分，并运用积分

(16)

其中Ln(x)为n阶变形Struve函数，则线圈产生的感应磁通密度为

(e2hpcosγ-1)e-j(mx+ny)-pzg1(u)dmdn。

(17)

(e2hpcosγ-1)e-j(mx+ny)-pzg1(u)dmdn。

(18)

(e2hpcosγ-1)e-j(mx+ny)-pzg1(u)dmdn。

(19)

3矩形截面圆柱线圈的受力计算

首先有

(20)

运用式(11)，式(12)得

(21)

(22)

(23)

(24)

(25)

其中

v=psinγ-jncosγ。

(26)

从而

(27)

(28)

(29)

(30)

(31)

将式(21)～式(25)中的I置换为NI/2h(R2-R1)，我们得到矩形截面圆柱线圈所受的力为

ez(-wy+jwxcosγ)]。

(32)

也就是说，导电板上方任意方位的圆柱线圈将只受到y与z方向的力，这是因为圆柱线圈关于x轴对称。对于轴线平行于导电平面的圆柱线圈，有γ=π/2，式(32)中各函数均将趋于0/0的不定式情形，显然此时仅有z向的力不为零，经过极限步骤

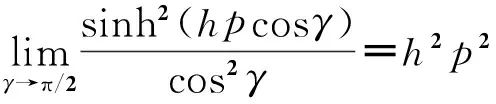
(33)

得到其值为

(34)

式(34)表明水平圆柱线圈的受力与线圈本身的长度无关。这是可以理解的，因为对无穷大金属板而言水平轴线圈的每匝都处于同等位置，每匝线圈与金属板的电磁相互作用特性是一样的，因此电磁力与匝数有关而与线圈长度无关。

4检验：线圈轴垂直于导电平面的特殊情形

现以线圈轴垂直于导电平面的特殊情形来检验式(32)的正确性。在这种情形有γ=0。对这种轴对称的场，应只有力的垂直分量而无水平分量。引入

(35)

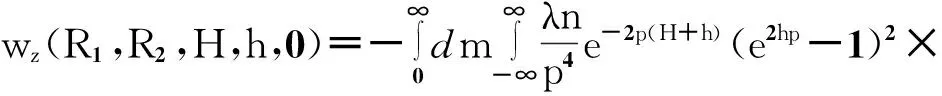
(36)

从而Fy=0。另一方面有

(37)

此式与文献[3]中给出的表达式一致。

5数值计算与比较

作为算例，取线圈参数H=0.1 m，h=0.03 m，R1=0.03 m，R2=0.08 m，N=500，激励电流参数为I=5 A，ω=2 000π rad/s，金属板参数κ=5.8×107S/m，μr=1(铜)，以式(32)计算Fy与Fz随夹角γ的变化值并绘制曲线图，并将此模型以有限元软件CST Studio仿真的结果进行验证，在仿真中分别取γ=0°，15°，30°，45°，60°，75°，90°。其结果如图2所示，图中的离散点即为CST的仿真计算结果。

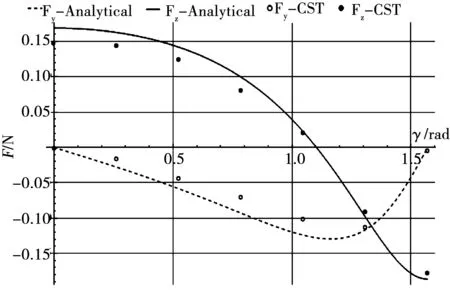
图2　圆柱线圈受力随夹角γ的变化Fig.2　　　　Forces acting on the cylindrical coils　　　 dependent on the axial angle γ

由图2可以看到，在我们所取的各项参数下，γ=0，π/2时Fy=0，且Fy有一最大值出现在γ=70°附近，随着γ的变化，Fy将保持方向不变。而Fz在γ=60°附近有一零点，过零之后Fz将反向。

保持其他各参数不变，取κ=1×107S/m(普通铁磁材料电导率)，我们观察式(34)所描述的水平轴圆柱线圈的受力随激励电流角频率ω变化的规律。分别绘制μr=1，μr=100，μr=1 000时的线圈受力曲线，并以将此模型以有限元软件CST Studio仿真的结果进行验证，在仿真中分别取ω=1 000，3 000，5 000，7 000，9 000 rad/s，其结果如图3所示，图中离散点为CST仿真结果。在此处的计算中假定μr为常数，即不考虑磁材料饱和以及磁滞的影响。

图3　平行轴圆柱线圈受力随电流角频率ω的变化Fig.3　　　　Forces acting on the cylindrical coils 　　　dependent on the axial angle ω

由图3可以看到，当μr=100，激励电流角频率ω约为4 000 rad/s时水平线圈受力平均值可以为零。μr=1，ω=0即线圈通以直流电时线圈受力为零，但在μr≠1的情形，ω=0时线圈受力并不为零。这实际上反映了铁磁材料对通电线圈的磁力作用。

6结论

借助高阶矢量势，我们能够解析地处理厚金属板上方的任意放置的矩形截面圆柱线圈的受力问题。除了线圈轴垂直或平行于导电平面的特殊情形，该线圈将受到两个方向的电磁作用力，其中水平力沿着线圈轴在z=0平面的投影方向，另一个力沿着垂直于导电平面的方向。当线圈轴垂直或平行于导电平面时，线圈将仅受到垂直于导电平面方向的作用力。随着线圈轴与z轴夹角γ的变化，垂直方向力分量的时间平均值将在某个特定γ处变为零。对于μr>1的金属板，线圈所受平均电磁力可能对某个特定电流频率变为零。电流角频率ω=0即激励电流为直流时，仅当μr=1时线圈所受电磁力才会为零。

参 考 文 献:

[1]RAJOTTE R J,DROUET M G.Experimental analysis of a fast acting circuit breaker mechanism—electrical aspects[J].IEEE Transactions on Power Apparatus and Systems,1975,94(1): 89-96.

[2]LIPINSKI W.Über die abschirmung stationäter magnetfelder von zylinderspuler[J].Archiv für Elektrotechnik,1976,58: 9-14.

[3]LIPINSKI W,SIKORA R.Verluste und kraftangriff von wirbelströmen im leitenden halbraum bei zylindersymmetrischen magnetischen wechselfeld[J].Archiv für Elektrotechnik,1975,57:173-175.

[4]HANNAKAM L.Wirbelströme im leitenden halbraum bei beliebiger form der erregenden leiterschleife[J].Archiv für Elektrotechnik,1972,54: 253-257.

[5]HANNAKAM L.Transienter skineffekt in einer platte endlicher dicke bei beliebiger form der erregenden leiterschleife[J].Archiv für Elektrotechnik,1978,60: 361-371.

[6]THEODOULIDIS T,SKARLATOS A.Eddy current interaction of an arbitrarily positioned probe coil with a conductive cylinder[J].IEEE Transactions on Magnetics,2012,48(8): 2392-2394.

[7]THEODOULIDIS T,DITCHBURN R J.Mutual impedance of cylindrical coils at an arbitrary position and orientation above a planar conductor[J].IEEE Transactions on Magnetics,2007,43(8): 3368-3370.

[8]THEODOULIDIS T.Analytical model for tilted coils in eddy-current nondestructive inspection[J].IEEE Transactions on Magnetics,2005,41(9): 2447-2454.

[9]MICOLAU G,PICHENOT G,PREMEL D,et al.Dyad-based model of the electric field in a conductive cylinder at eddy-current frequencies[J].IEEE Transactions on Magnetics,2004,40(2): 400-409.

[10]MIORELLI R.Eddy current modeling of narrow cracks in planar-layered metal structures[J].IEEE Transactions on Magnetics,2012,48(10): 2551-2559.

(编辑：刘琳琳)

Calculations for electromagnetic forces between thick metal plates and cylindrical coils of arbitrary location

LUO Yao

(School of Electrical Engineering,Wuhan University,Wuhan 430072,China)

Abstract:For an inclined circular coil with alternating current excitation and placed above a thick metal plate,analytical solution of electromagnetic forces between them can not be found by traditional methods.Using the high-order vector potential,the problem was solved analytically,and vector analysis and Struve functions were employed to simplify the final results.The expressions for the electromagnetic forces acting on the cylindrical coil of arbitrary position were obtained.The results indicate that there are at most two electromagnetic forces acting on the coils.When the axes of coils are perpendicular or parallel to the conducting surface,the results can be simplified to 1-D integrals and only perpendicular component exists.The numerical calculations were implemented to verify the obtained results.The results show that the time mean value of the vertical force component can vanish for certain inclined angles of coil axis,and the horizontal force component can attain maximum value for some other angles.If direct currents flow through the coil,the electromagnetic forces will vanish only when the plate has the same permeability with the air.

Keywords:cylindrical coils; electromagnetic force；high-order vector potential; Bessel functions; Struve functions

收稿日期:2013-05-04

基金项目：国家自然科学基金青年基金(51507115)

作者简介:罗垚(1983—)，男，博士，研究方向为电磁场计算及数学物理方程。

通讯作者:罗垚

DOI:10.15938/j.emc.2016.05.004

中图分类号:TM 12

文献标志码:A

文章编号:1007-449X(2016)05-0023-05