高超声速飞行器RBF神经网络滑模变结构控制

王建敏，　董小萌，　吴云洁

(1.北京航空航天大学 自动化科学与电气工程学院，北京 100191; 2.中国科学院空间应用工程与技术中心，北京 100094;3.中国空间技术研究院 钱学森空间技术实验室，北京 100094; 4.北京航空航天大学 虚拟现实技术与系统国家重点实验室，北京 100191)



高超声速飞行器RBF神经网络滑模变结构控制

王建敏1,2，董小萌3，吴云洁1,4

(1.北京航空航天大学 自动化科学与电气工程学院，北京 100191; 2.中国科学院空间应用工程与技术中心，北京 100094;3.中国空间技术研究院 钱学森空间技术实验室，北京 100094; 4.北京航空航天大学 虚拟现实技术与系统国家重点实验室，北京 100191)

摘要:针对高超声速飞行器高度非线性及强耦合的特点，提出了一种基于RBF神经网络调参的滑模变结构控制器。滑模变结构控制器能够使高超声速飞行器稳定飞行，但在系统状态到达滑模面后会产生剧烈的抖振现象，不利于工程应用。RBF神经网络在一定条件下可以任意精度逼近非线性函数，且具有较强的自学习、自适应和自组织能力。将RBF神经网络与滑模变结构控制相结合，一定程度上能够消除滑模控制的抖振问题。在高超声速飞行器的巡航状态下，分别加入高度阶跃指令和速度阶跃指令进行了仿真。仿真结果表明，所设计的RBF神经网络滑模变结构控制器使高超声速飞行器在保证快速性、鲁棒性和抗干扰性的同时，克服了执行机构的抖振问题。

关键词:高超声速飞行器；RBF神经网络；滑模变结构；控制；抖振

0引言

高超声速飞行器是指飞行在距地面30-70 km的近空间领域、飞行马赫数大于5的一类飞行器。由于近空间领域大气环境不稳定，飞行条件复杂，再加上高超声速飞行器气动外形的特点及其对参数变化的灵敏性高，因此对高超声速飞行器的控制不是一项简单的任务。从上世纪60年代开始，美国就开始研究高超声速飞行器。经过五十多年的发展，对高超声速飞行器的制导控制的研究已日趋成熟，各种各样的控制方法被应用于高超声速飞行器的制导控制中，并取得了满意的效果。文献[1]对高超声速飞行器的气动力和气动弹性进行了详细的分析，为高超声速飞行器的模型建立奠定了基础。文献[2]在结构和空气动力学分析的基础上，建立了面向控制的吸气式高超声速飞行器的模型，为控制器的设计提供了方便。在高超声速飞行器控制器的设计中，有应用动态逆控制的，有应用线性二次型鲁棒控制方法的，有利用动态面进行设计的，也有利用滑模变结构进行控制律的构建的，不同的方法都有其各自的优势，均在某一方面达到了良好的控制效果。文献[3-4]利用滑模控制方法为高超声速飞行器设计了控制律，并利用自适应滑模变结构方法设计了鲁棒控制器和观测器。

滑模控制的一个主要缺点是存在抖振问题。文献[3-4]中用饱和函数代替了符号函数，并在滑模面附近设计了边界层。这种方法虽然达到了削弱抖振的目的，但该方法具有保守性。针对滑模抖振抑制问题，胡强晖[5]等将状态的差值作为滑模增益，设计了变增益滑模控制器，当状态跟踪误差为零时，滑模增益为零也即消除了抖振；殷明[6]等设计了积分滑模面，通过对切换信号的积分作用消除抖振；赖志林[7]等设计了普通滑模面与积分滑模面的多模切换系统，同样利用积分作用消除抖振；文献[8-9]利用模糊理论估计滑模控制器的增益，以此来减小抖振；吴忠强[10]等利用高阶滑模的时间积分作用达到了消除抖振的目的。

在上述抖振抑制方法的启发下，本文考虑用神经网络的逼近特性消除滑模抖振问题。径向基函数(Radial Basis Function,RBF)神经网络，是一种局部逼近网络，能以任意精度逼近任一连续函数。RBF神经网络的这种特性使得它被广泛应用于系统中参数的估计与辨识，并与其他控制方法相结合设计出了多种多样的神经网络控制方法。姚兰[11]等利用神经网络的逼近特性对系统中的不确定项在线辨识，再加入到滑模控制中，设计了神经网络参数辨识的滑模控制器。文献[12]用滑模方法设计等效控制，用RBF神经网络设计补偿控制器，对系统模型的不确定部分进行补偿。高新[13]设计的神经网络滑模控制器是利用滑模控制的到达条件作为RBF神经网络的输入参量，经过自适应学习获得控制量。吴勃[14]等利用RBF神经网络对滑模控制的切换增益进行辨识，但其学习算法只是简单的采用梯度下降法，设计的控制器也具有一定的保守性。

针对上述文献中将滑模控制与RBF神经网络输出直接相加易导致控制缓慢且RBF神经网络学习算法单一的问题，本文设计了基于RBF神经网络调参的滑模变结构控制方法。利用RBF神经网络的逼近特性，实时调整滑模控制的增益参数，以达到消除系统抖振，并保证系统的快速性和鲁棒性的目标。同时在RBF神经网络学习算法中采用多种自学习方法，以防止学习过程陷入局部寻优当中。此外，针对高超声速飞行器非线性、强耦合的特点，控制器的设计多采用滑模变结构鲁棒控制方法，而此方法中滑模增益的调节是一项关键又繁琐的工作。借助本文设计的RBF神经网络调参方法将极大的提高效率。

1高超声速飞行器模型

美国NASA兰利研究中心发布的通用吸气式高超声速飞行器的纵向动态模型可描述为速度、高度、攻角、航迹角及俯仰角速率的微分方程的形式[3]

(1)

式中，V,h,γ,α,q分别为高超声速飞行器的速度、高度、航迹角、攻角和俯仰角速率；m,Iyy分别为飞行器的质量和转动惯量；L,D,T,Myy,r分别为飞行器受到的升力、阻力、推力、俯仰转动力矩和飞行器距地心的距离，且可分别表达为

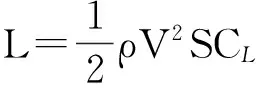
(2)

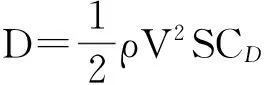
(3)

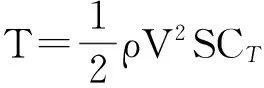
(4)

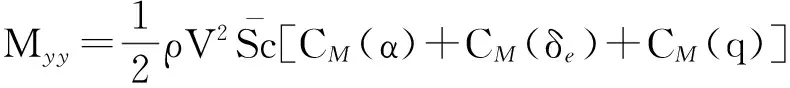
(5)

r=h+RE。

(6)

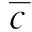
高超声速飞行器的发动机可建模为二阶系统

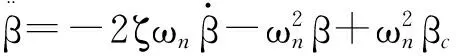
(7)

其中，β为油门量开度。

为了验证控制器对参数变化的鲁棒性和抗干扰性能，在模型中加入了一定的不确定性，即

(8)

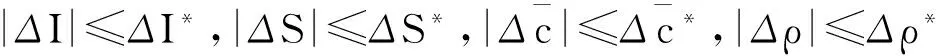
2滑模控制律设计

2.1模型线性化

高超声速飞行器的模型(1)是非线性且强耦合的，为了设计控制律需要应用反馈线性化原理进行线性化处理。在模型(1)中设速度V和高度h为输出量，令发动机油门量βc和舵偏角δe为输入量(控制量)，则线性化的目标就是在V和h的方程中能显式表达与βc和δe的关系。根据非线性方程中系统的相对度与系统阶数的关系[15]，将V和h分别微分3次和4次即可出现输入量βc和δe，即

(9)

式中：

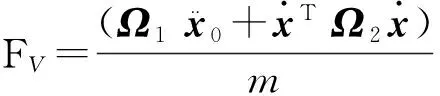
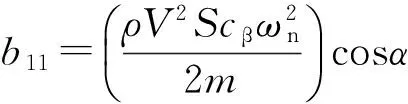
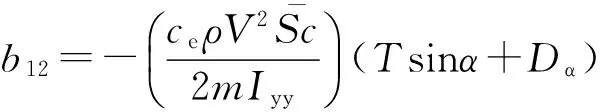
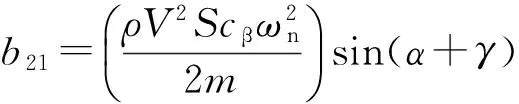
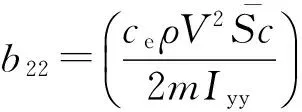
2.2滑模控制律设计

从线性化后的模型方程(9)可以看到，速度通道和高度通道形成了两个独立的表达式，因此可以分别设计速度通道和高度通道的控制律。则滑模面[3,16]可以分别设计为：

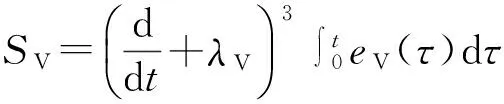
(10)

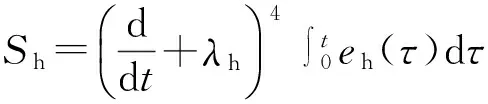
(11)

其中，eV=V-Vd为速度的跟踪误差；eh=h-hd为高度的跟踪误差。

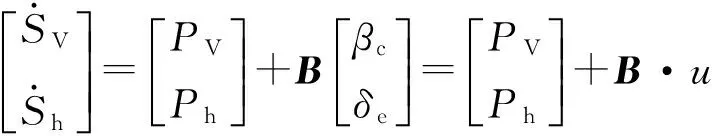
(12)

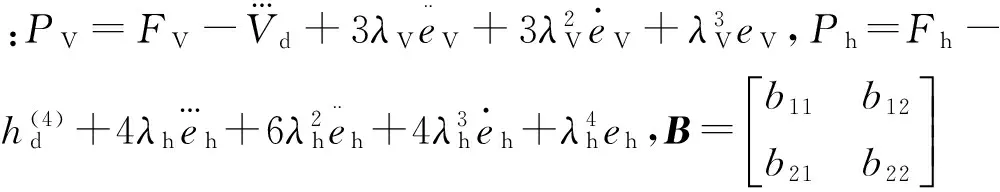
在式(12)的基础上，设计基于指数趋近律[18]的滑模控制律为

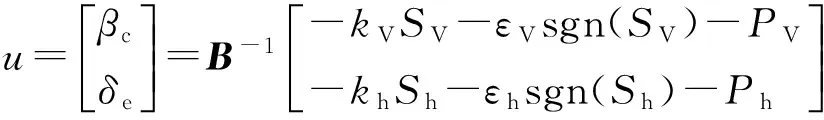
(13)

其中，kV>0,kh>0,εV>0,εh>0。

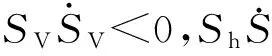
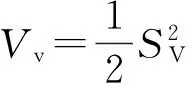
(14)

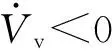
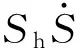
为了进一步消除抖振，将符号函数做如下平滑处理：

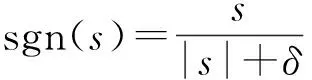
(15)

其中，δ是很小的正数。

3神经网络调参律

利用RBF神经网络的逼近特性设计了控制增益的调参律，实时在线的调整参数k的大小，以达到减小、消除抖振的作用。同时根据定理1可以得知，只要所调整的参数k大于零，就可以保证控制器的稳定性。

这里RBF神经网络采用三层前向网络：第一层是多路输入误差信号及其导数；第二层隐含层采用高斯函数作为基函数；第三层为输出层，输出所调参数值。由于速度通道与高度通道两个子系统是独立的，因此这里也分开设计两个通道的神经网络调参律。

3.1速度通道神经网络调参律

在速度通道子系统中，神经网络采用3-7-1的结构，即输入层有3个参数，隐含层有7个神经元结点，输出层有1个参数，其映射关系如图1所示。

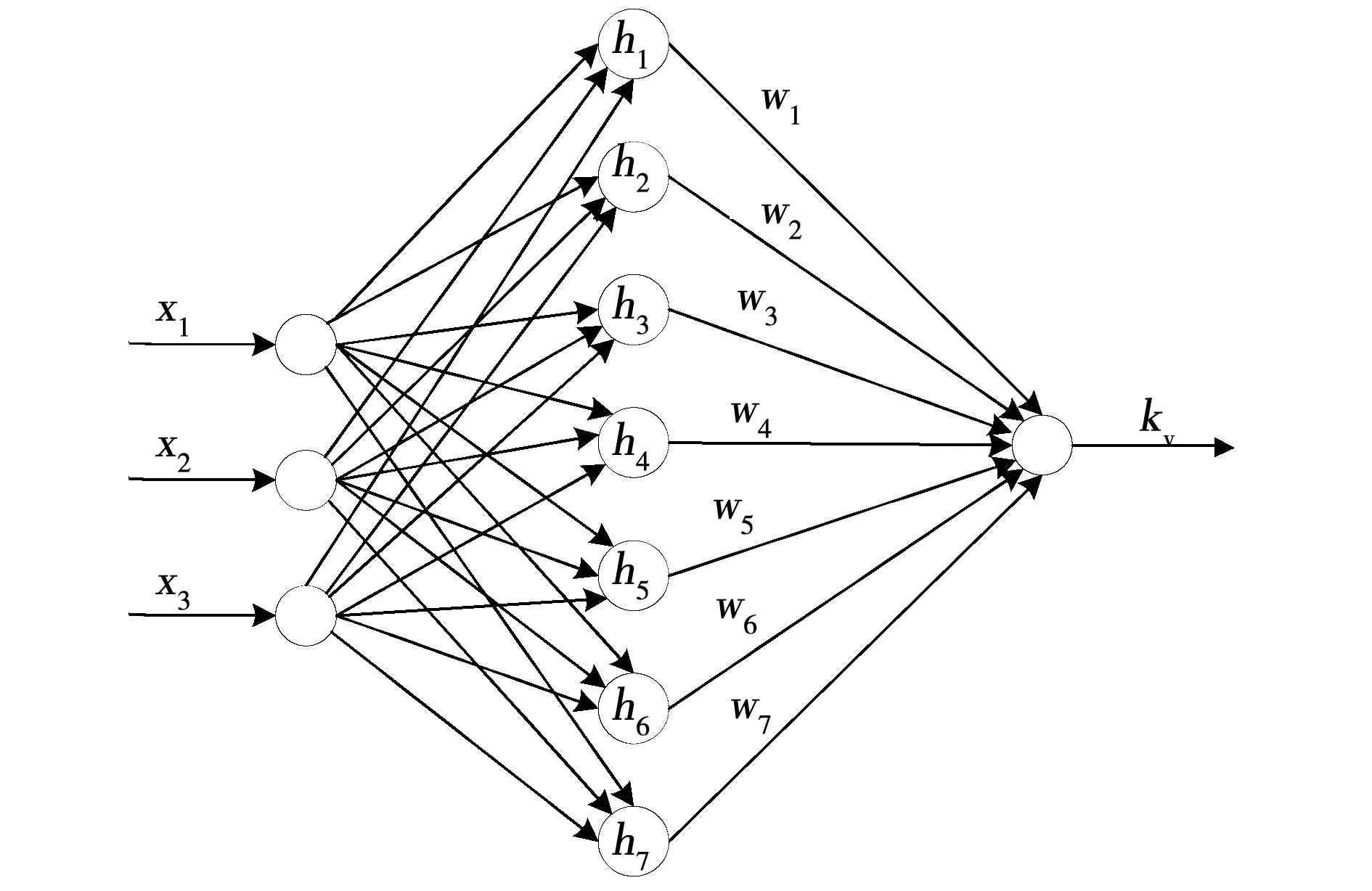
图1　速度子系统神经网络设计Fig.1　Design of neural network for velocity subsystem

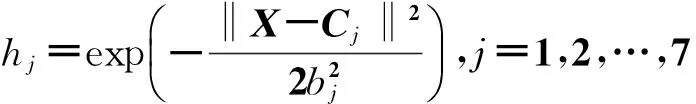
(16)

Cj=[Cj1,Cj2,Cj3]T,j=1,2,…,7。

(17)

B=[b1,b2,…,b7]T为节点中心向量，输出权值向量为W=[w1,w2,…,w7]，因此经过神经网络计算后输出参数为

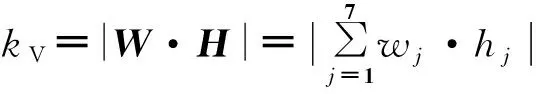
(18)

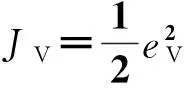
j=1,2,…,7。

(19)

则节点中心值为

bj=b1j+η·Δbj+μ(b1j-b2j)。

(20)

其中：b1j为bj前一周期的值，b2j为b1j前一周期的值。

基宽变化值描述为

j=1,2,…,7;i=1,2,3。

(21)

则节点基宽值为

Cji=C1ji+η·ΔCji+μ(C1ji-C2ji)。

(22)

其中：C1ji为Cji前一周期的值，C2ji为C1ji前一周期的值。

输出权值变化可描述为

-eV·hj·sgn(kV)

j=1,2,…,7。

(23)

则输出权值为

wj=w1j+η·Δwj+μ·(w1j-w2j)。

(24)

其中：w1j为wj前一周期的值，w2j为w1j前一周期的值。

此外，式(20)、式(22)、式(24)中的η为学习速率，μ为学习因子，且满足0<η<1，0<μ<1。

3.2高度通道神经网络调参律

高度通道子系统中因其有4个不同的输入参数需考虑，故神经网络设计为4-9-1结构，其映射关系如图2所示。

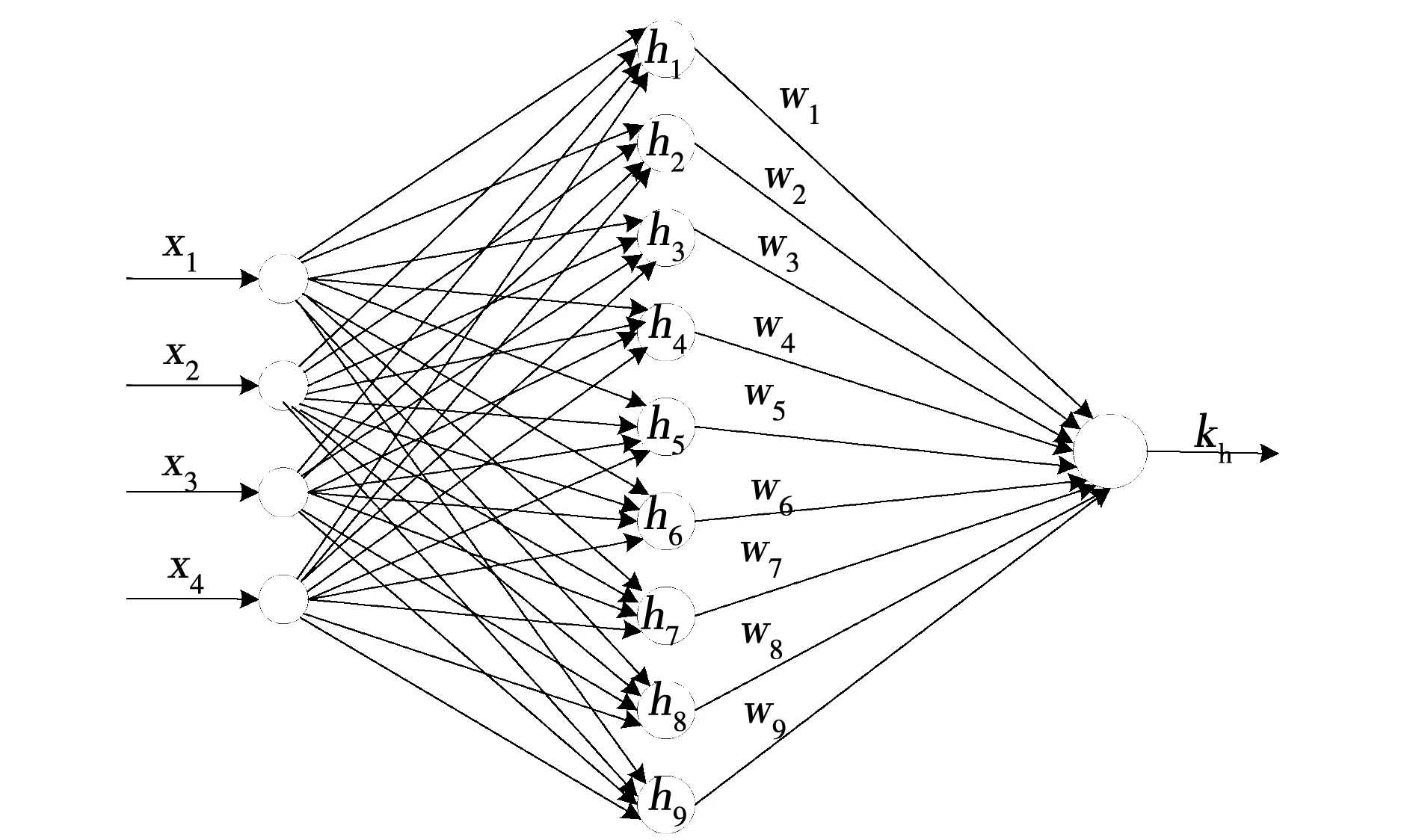
图2　高度子系统神经网络设计Fig.2　Design of neural network for altitude subsystem

Chj=[Chj1,Chj2,Chj3,Chj4]T,j=1,2,…,9,

(25)

Bh=[bh1,bh2,…,bh9]T,

(26)

Wh=[wh1,wh2,…,wh9]。

(27)

则神经网络的输出为

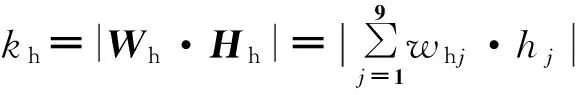
(28)

为了增强调参律对不确定性的适应能力，速度和高度两个通道采用了不同的学习算法。因此在这里神经网络中节点中心的自组织学习采用K-均值聚类方法，基宽向量根据所确定的节点中心寻找最大距离来确定，而输出权值的学习则采用LMS方法[20]，其具体方法分别为：

(1)K-均值聚类方法

第一步初始化聚类中心，随机产生9组不同的样本作为初始中心Cji(0),(j=1,2,…,9;i=1,…4)；

第二步随着新输入样本的出现，更新输入向量Xh；

第三步寻找新输入的向量Xh离哪个中心最近，即找到j(Xh)使其满足

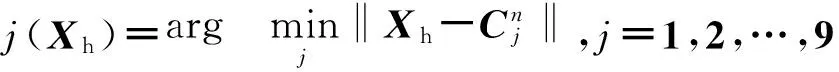
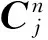
第四步调整中心

式中，σ是学习步长且0<σ<1；

第五步判断是否学完所有样本且中心分布不再变化，是则结束，否则n=n+1转到第二步。

(2)基宽参数确定

根据每一步迭代的中心向量，可确定出当前的基宽参数，即

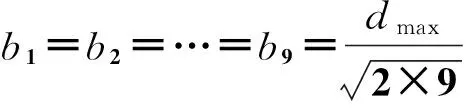
其中，dmax为所选取的中心之间的最大距离。

(3)LMS方法

对输出权值的自组织学习采用LMS方法，其具体步骤为：

第一步初始化，赋给Wj(0)各1个较小的随机非零值；

第二步对一组新输入向量Xh和对应的期望输出d，计算径向基向量Hh，然后利用

e(n)=d(n)-Wh(n)·Hh(n)，

Wh(n+1)=Wh(n)+η·Ηh(n)·e(n)，

对输出权值进行更新；

第三步判断是否满足条件，若满足则算法结束，否则将n值加1，转到第二步重新执行。

4仿真分析

结合前文所述的神经网络调参律，采用基于RBF神经网络的滑模变结构控制器控制高超声速飞行器，并进行了仿真验证。

仿真基于高超声速飞行器的巡航状态，即高度为33 528m、速度为4 590m/s、马赫数为15、攻角为0°、俯仰角速率为0°/s。高超声速飞行器发动机模型中阻尼比和自然频率分别选择0.7和5rad/s。仿真中速度通道子系统给予不同的速度阶跃指令，高度通道子系统加入不同的高度阶跃指令。则基于RBF滑模控制器的高超声速飞行器速度通道和高度通道阶跃响应分别如图3和图4所示。在仿真结果中，给出的速度和高度曲线是在阶跃指令激励下的变化曲线，是消去了巡航状态的基础值的，因此各曲线均是从0开始。

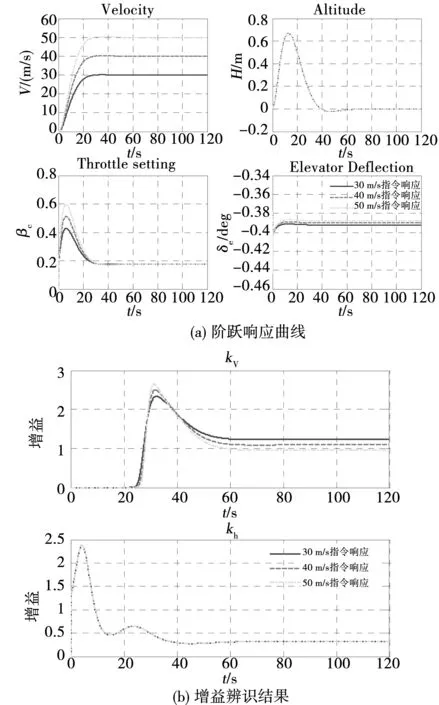
图3　RBF滑模控制速度通道阶跃响应Fig.3　　　　Speed subsystem step response of 　　　RBF sliding mode control

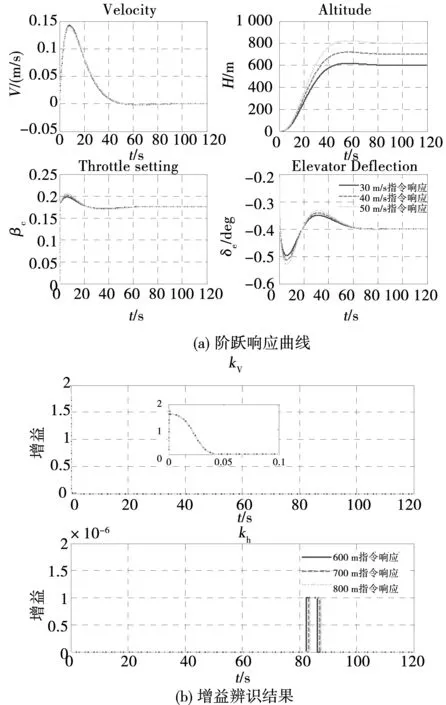
图4　RBF滑模控制高度通道阶跃响应Fig.4　　　　Altitude subsystem step response of 　　　RBF sliding mode control

图3是高超声速飞行器在30m/s、40m/s和50m/s3种不同速度指令下的阶跃响应结果。从图3(a)可见，在不同的指令下系统均能在25s左右跟踪到指令，并最终保持系统稳定。图3(a)中下面的两个图表示执行器响应曲线，从图中可见该曲线光滑收敛，没有抖动现象。

图4是高超声速飞行器在600m、700m和800m3种不同的高度指令下的阶跃响应结果。从图4(a)可见，系统均能在经过一定时间的跟踪后稳定到指令值，说明系统具有良好的稳定性。图4(a)中下面的2个执行器曲线光滑收敛，没有抖振现象出现。由此说明，提出的方法有效的消除了滑模的抖振问题。

图3(b)和图4(b)分别是速度通道和高度通道阶跃响应时的参数辨识结果。从两组图中可以看到，滑模增益经过一定时间的辨识后均稳定为大于零的数，因此根据定理1也可以证明所设计的控制器是稳定的。

为了验证文中设计的RBF神经网络滑模控制器的鲁棒性和抗干扰性能，在模型中加入式(8)所示的参数不确定性，同样进行系统的阶跃响应仿真。同时为了证明所设计方法的有效性，将其与边界层滑模抖振抑制方法进行了对比，如图5和图6所示。

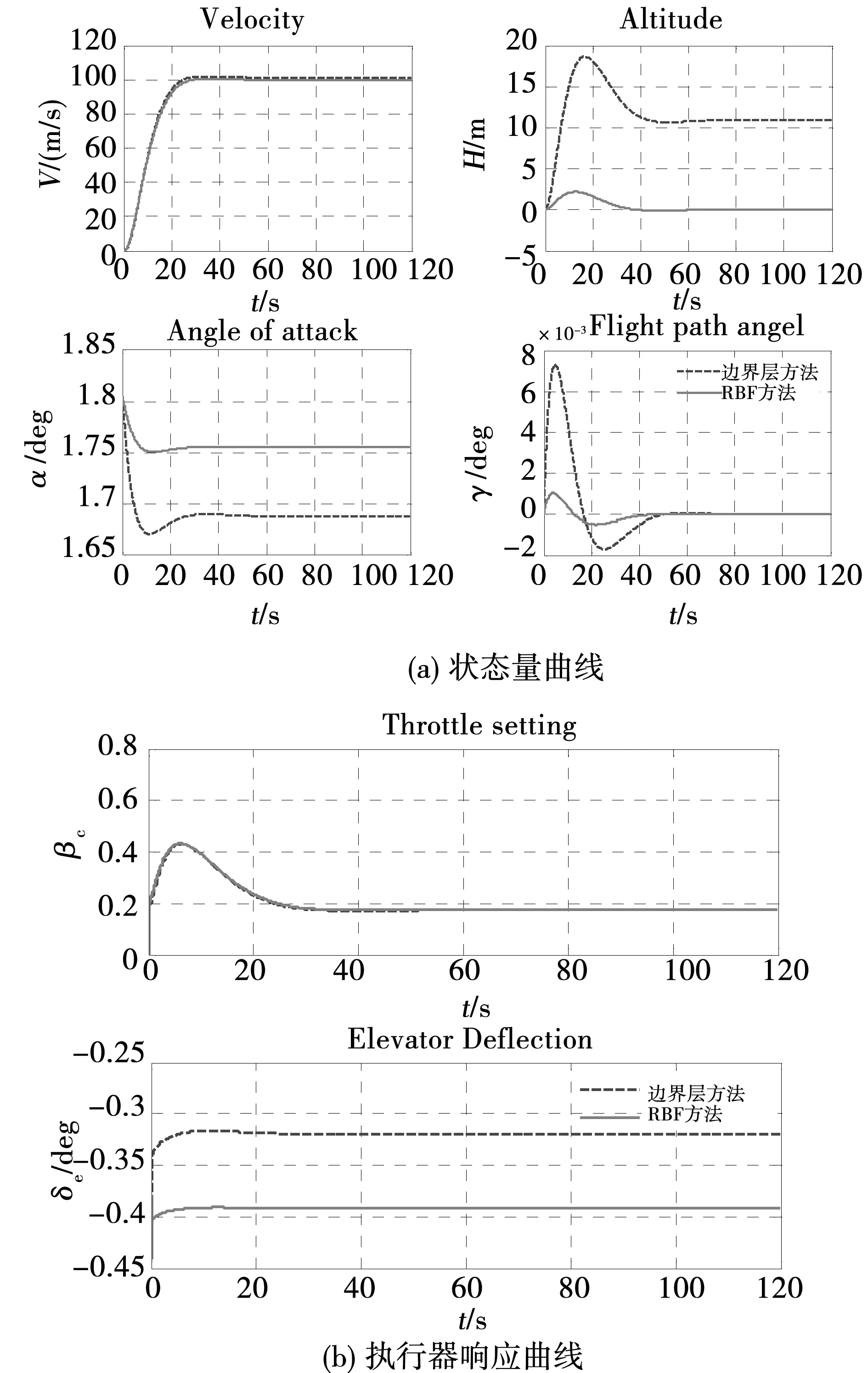
图5　不确定性系统的速度通道阶跃响应对比Fig.5　　　　Comparison of speed subsystem step 　　　response of uncertainty system

由图5(b)的执行器曲线可见，此方法与边界层方法均可以达到消除抖振的目的。图5(a)中，此方法与边界层方法的速度响应曲线基本吻合，而其他状态量的响应曲线中，此方法则明显优于边界层方法。由于边界层方法在系统状态到达边界层内以后系统的鲁棒性大大降低，因此图5(a)中右上角的高度曲线明显没有收敛到期望值0。

同样的，图6(b)中的执行器响应曲线中，此方法与边界层方法均消除了滑模抖振问题。但从图6(a)可见，此方法在鲁棒性方面要优于边界层方法。而且在系统的响应时间上，这里提出的RBF神经网络方法的响应速度并不逊色于边界层方法。

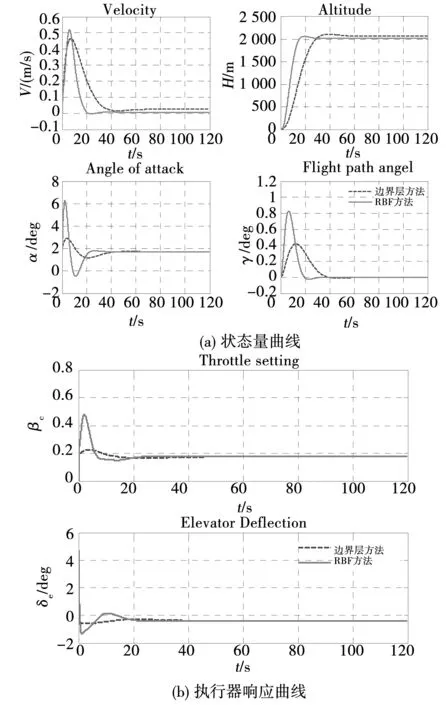
图6　不确定性系统的高度通道阶跃响应对比Fig.6　　　　Comparison of altitude subsystem step 　　　response of uncertainty system

综上所述，所设计的基于RBF神经网络调参律的滑模控制器具有较好的鲁棒性和抗干扰性，对高超声速飞行器的控制能够达到较为满意的效果。

5结论

针对高超声速飞行器高度非线性、强耦合的特点，设计了基于RBF神经网络调参律的滑模控制器。该控制器在保证系统鲁棒性的同时极大的简化了参数的选择过程，可根据输入在线调整参数，方便了工程应用。将RBF神经网络与滑模控制器相结合，既能保留滑模控制的快速性、鲁棒性和抗干扰性等特性，又可以实时调整控制参数，达到减弱、消除抖振的目的。最后针对高超声速飞行器的巡航状态进行了仿真，并与边界层方法进行了对比。仿真结果表明，基于RBF神经网络调参律的滑模控制器相比于传统的边界层滑模方法，具有较好的鲁棒性和抗干扰性，在使系统稳定跟踪指令的前提下大大削弱了抖振，达到了满意的效果。

参 考 文 献:

[1]CHAVEZ R Frank,SCHMIDT K David.Analytical Aeropropulsive/Aeroelastic hypersonic vehicle model with dynamic analysis[J].Journal of Guidance,Control and Dynamics,1994,17(6):1308-1319.

[2]PARKER T Jason,BOLENDER A Michael,DOMAN B David.Control-Oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance,Control and Dynamics,2007,30(3):856-869.

[3]XU H Jian,M D Maj,I A Petros.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance,Control and Dynamics,2004,27(5):829-838.

[4]HU Xiao X,WANG Li G,H Chang H,et al.Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle[J].Journal of the Franklin Institute,2012,349:559-577.

[5]胡强晖,胡勤丰.全局滑模控制在永磁同步电机位置伺服中的应用[J].中国电机工程学报,2011,31(18):61-66.

HU Qianghui,HU Qinfeng.Global sliding mode control for permanent magnet synchronous motor servo system [J].Proceedings of the CSEE,2011,31(18):61-66.

[6]殷明,陆宇平,何真,等.变体飞行器变形辅助机动的建模与滑模控制[J].系统工程与电子技术,2015,37(1):128-134.

YIN Ming,LU Yuping,HE Zhen,et al.Modeling and sliding mode control of morphing aircraft for morphing-aided maneuver [J].Systems Engineering and Electronics,2015,37(1):128-134.

[7]赖志林,刘向东,陈振,等.压电陶瓷执行器多模时变滑模逆补偿控制[J].电机与控制学报,2012,16(1):92-96,103.

LAI Zhilin,LIU Xiangdong,CHEN Zhen,et al.Multi-mode time-varying sliding mode control of Piezoceramic actuator based on inverse compensation [J].Electric Machines and Control,2012,16(1):92-96,103.

[8]胡盛斌,陆敏恂.空间三关节机器人自适应双模糊滑模控制[J].同济大学学报：自然科学版,2012,40(4):622-628.

HU Shengbin,LU Minxun.Adaptive double fuzzy sliding mode control for three-links spatial robot[J].Journal of Tongji University：Natural Science,2012,40(4):622-628.

[9]靳宝全,熊诗波,程珩.电液位置伺服系统的变速趋近律滑模控制抖振抑制[J].机械工程学报,2013,49(10):163-169.

JIN Baoquan,XIONG Shibo,CHENG Hang.Chattering inhibition of variable rate reaching law sliding mode control for electro-hydraulic position servo system [J].Journal of Mechanical Engineering,2013,49(10):163-169.

[10]吴忠强,谢建平.带扰动观测器的网侧逆变器高阶终端滑模控制[J].电机与控制学报,2014,18(2):96-101.

WU Zhongqiang,XIE Jianping.High-orderterminal sliding mode control of grid-connected inverter with disturbance observer [J].Electric Machines and Control,2014,18(2):96-101.

[11]姚兰,肖建,王嵩,等.自组织区间二型模糊神经网络及其自适应学习算法[J].控制理论与应用,2013,30(6):785-791.

YAO Lan,XIAO Jian,WANG Song,et al.Interval type-2 fuzzy neural networks with self-organizing structure and adaptive learning algorithm[J].Control Theory & Applications,2013,30(6):785-791.

[12]Niu J J,Fu Y L,Qi X Y.Design and application of discrete sliding mode control with RBF network-based switching law[J].Chinese Journal of Aeronautics,2009,22:279-284.

[13]高新.基于神经网络变结构控制的机械臂系统研究[D].哈尔滨:哈尔滨理工大学,2012.

[14]吴勃,许文芳,陈虹丽.神经滑模控制在机器人轨迹跟踪中的应用[J].电机与控制学报,2009,13(增1):99-104.

WU Bo,XU Wenfang,CHEN Hongli.Application of neural networks sliding mode control in tracking control of robot manipulators[J].Electric Machines and Control,2009,13(suppl 1):99-104.

[15]J J E Slotine.应用非线性控制[M].程代展 译.北京：机械工业出版社,2006:138-150.

[16]J-J E Slotine,J A Coetsee.Adaptive sliding controller synthesis for non-linear systems[J].INT.J.Control,1986,43(2):1631-1651.

[17]WANG Qian,STENGEL F Robert.Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance,Control and Dynamic,2000,23(4):577-585.

[18]高为炳,程勉.变结构控制系统的品质控制[J].控制与决策,1989,4:1-6.

GAO Weibing,CHENG Mian.Quality control of variable structure control systems[J].Control and Decision,1989,4:1-6.

[19]乔俊飞,韩红桂.RBF神经网络的结构动态优化设计[J].自动化学报,2010,36(6):865-872.

QIAO J F,HAN H G.Optimal structure design for RBFNN structure[J].Acta Automatica Sinica,2010,36(6):865-872.

[20]高隽.人工神经网络原理及仿真实例[M].北京：机械工业出版社,2003:55-65.

(编辑：张楠)

Hypersonic flight vehicle of sliding mode variable structure control based on RBF neural network

WANG Jian-min1,2,DONG Xiao-meng3,WU Yun-jie1,4

(1.School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China; 2.Technology and Engineering Center for Space Utilization,Chinese Academy of Sciences,Beijing 100094,China; 3.Qian Xuesen Laboratory of Space Technology,CAST,Beijing 100094,China; 4.State Key Laboratory of Virtual Reality Technology and Systems,Beihang University,Beijing 100191,China)

Abstract:According to hypersonic flight vehicle of highly nonlinear and strong coupling characteristics,sliding mode variable structure control based on RBF neural network regulating parameters was proposed.Sliding mode variable structure controller makes the hypersonic flight vehicle stably fly,but when the system states arrived at the sliding mode surface,it will emerge severe chattering,which would influence engineering applications.RBF neural networks can approximate nonlinear functions in arbitrary precision under certain conditions,in addition it has capacity of strong self-learning,adaptive and self-organizing.The controller that together RBF neural network with sliding mode variable structure can eliminate chattering problem generated by sliding mode variable structure control to a certain extent.Simulation was conducted by giving altitude and velocity command on the cruise condition of hypersonic flight vehicles.Simulation results show that RBF neural network based sliding mode variable structure controller designed here ensures rapidity,robustness and immunity of the hypersonic flight vehicle,while overcoming the problems of actuator chattering.

Keywords:hypersonic flight vehicle; RBF neural network; sliding mode variable structure; control; chattering

收稿日期:2014-04-08

基金项目：国家自然科学基金(91216304)

作者简介：王建敏(1986—),男,博士，研究方向为伺服控制、导弹制导控制、高超声速飞行器制导控制；董小萌(1978—),男,高级工程师，研究方向为目标跟踪、飞行器控制与建模;吴云洁(1969—),女,博士，教授，博士生导师，研究方向为智能控制理论、半实物仿真设备及工业过程控制等。

通讯作者:王建敏

DOI:10.15938/j.emc.2016.05.015

中图分类号:V 448

文献标志码:A

文章编号:1007-449X(2016)05-0103-08