感应电机Super-twisting算法定子磁链观测器设计

潘月斗，　陈涛，　陈泽平

(1.北京科技大学 自动化学院，北京100083；2.北京科技大学 钢铁流程先进控制教育部重点实验室，北京100083)



感应电机Super-twisting算法定子磁链观测器设计

潘月斗1,2，陈涛1,2，陈泽平1,2

(1.北京科技大学 自动化学院，北京100083；2.北京科技大学 钢铁流程先进控制教育部重点实验室，北京100083)

摘要:为了提高感应电机定子磁链的观测精确度，提出了一种基于Super-twisting算法的磁链观测方法，设计了定子磁链观测器，并应用到感应电机直接转矩控制中。依据滑模变结构控制的鲁棒性特点来抑制多输入多输出定子磁链观测器系统中的扰动。利用Super-twisting算法所需信息少的优点，设计了简单的控制律，从而更适合于实际工程应用。在对观测器稳定性进行分析时，将转速和耦合量看作扰动来处理，并给出了系统一致渐近稳定的充分条件。与常规电压模型法相比，基于Super-twisting算法的定子磁链估算值更加准确，且对电机定子电阻参数变化具有更强的鲁棒性。仿真和实验结果验证了该方法的有效性。

关键词:感应电机；Super-twisting算法；磁链观测；电流观测；直接转矩控制

0引言

感应电机具有结构简单、制造容易、坚固耐用、价格便宜、运行可靠、维护方便、运行效率高、转动惯量小、动态响应快、使用环境和结构发展不受限制等优点[1]，被广泛应用于工农业生产、国防、科技及社会生活等各个方面。随着直接转矩控制和矢量控制技术的出现，使其逐渐进入了伺服控制领域[2]。直接转矩控制方法是把转矩作为被控量，并由电流和定子磁链估算，定子磁链观测值的精确度直接影响直接转矩控制的控制效果[3]。

定子磁链观测的基本方法有电压模型法和电流模型法。电压模型法结构简单，观测时仅需确定定子电阻，因此对定子电阻参数值准确度要求较高。但是在实际应用中，很难精确地确定定子电阻参数，而且定子电阻参数受各种因素影响会发生变化，这就造成了对定子磁链的观测不准确。另外，电压模型法在运算过程中需开环积分(纯积分)，微小的直流偏移误差和初始值误差都将导致积分饱和[4]。电流模型法可解决电压模型积分漂移和无法建立初始磁链的问题，但观测精度与转速相关，易受电动机转速变化的影响[5]。为了更好的观测磁链，已提出了很多方法，如模型参考自适应方法[6]、卡尔曼滤波器方法[7-8]、神经网络方法[9]、滑模变结构方法[10-11]等。相比其他方法，滑模变结构方法对系统的不确定性因素具有较强的鲁棒性和抗干扰性，同时控制设计简单，物理上易于实现，因此得到广泛应用。

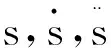
1感应电机的数学模型

设感应电机的磁路是线性的，忽略铁损的影响， 在静止坐标系(α-β)下，三相鼠笼型感应电机的数学模型的状态方程为

(1)

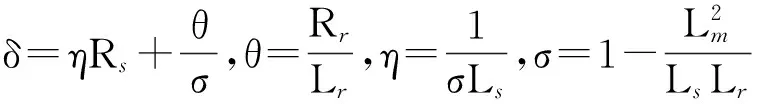
2Super-twisting算法磁链观测器设计

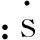
针对式(2)所示的一类SISO(single input single output)系统，Super-twisting算法状态观测器设计的一般参考形式如式(3)所示[14]。

(2)

(3)

感应电机是一个MIMO(multiple input multiple output)系统，与式(2)所述系统相比，式(1)所示的感应电机模型更加复杂。选取与式(3)类似的滑模变量，将电流跟踪误差作为滑模变量，从而设计简单的控制信号。基于Super-twisting算法的感应电机定子磁链观测器如下：

(4)

(5)

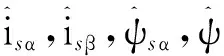
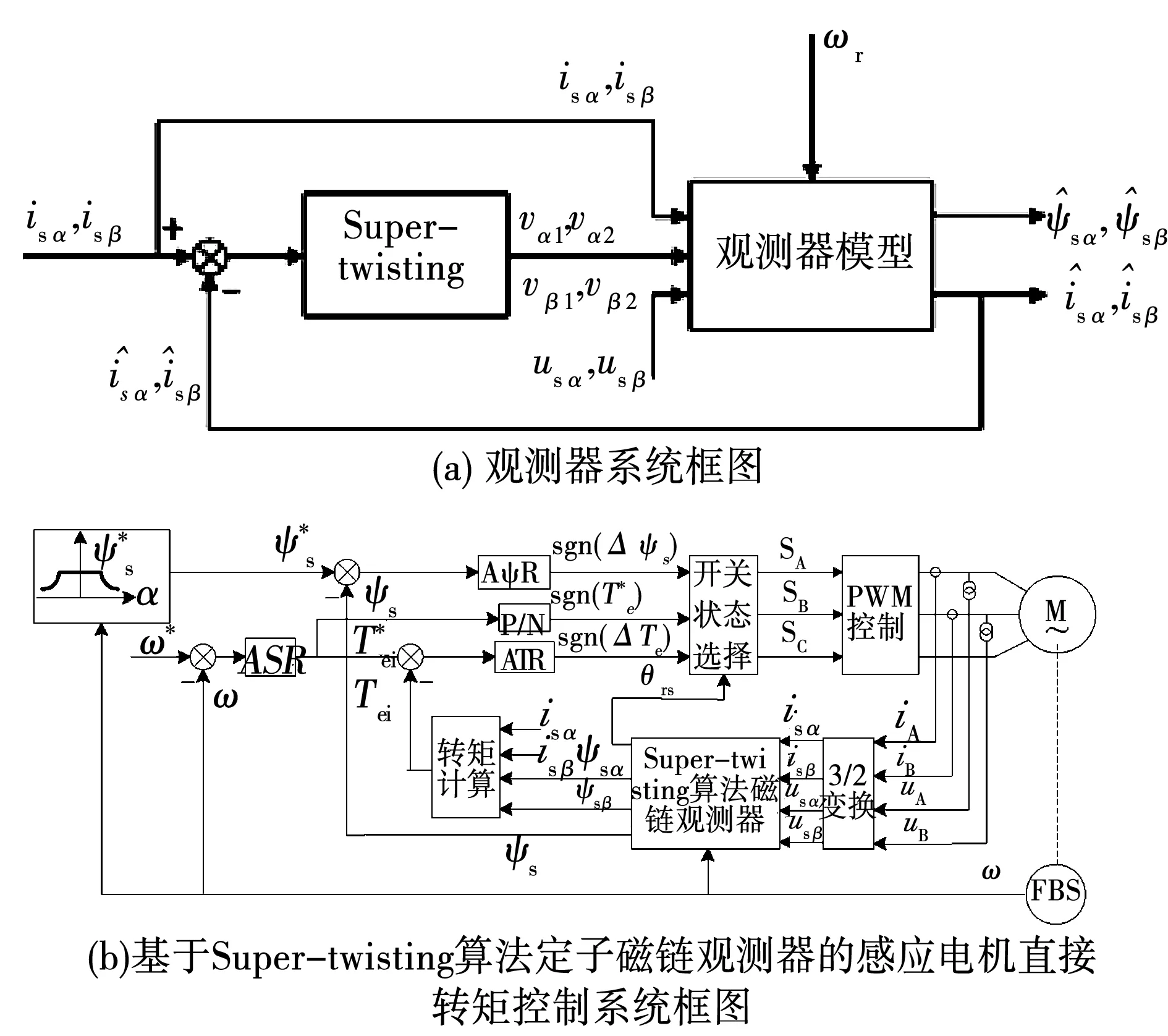
图1　系统框图Fig.1　Diagram of the system

3观测器稳定性分析

式(3)减式(4)，可以得到定子电流和定子磁链观测误差方程：

(6)

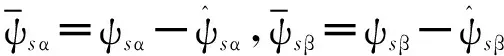
将式(6)写成如下形式[15]:

(7)

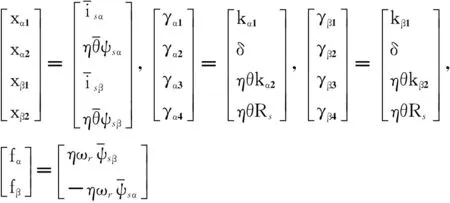
(8)

上式限定了系统不确定性的界，其中，常数ζα1、ζα2、ζβ1、ζβ2≥0。

选取如下Lyapunov函数[15]:

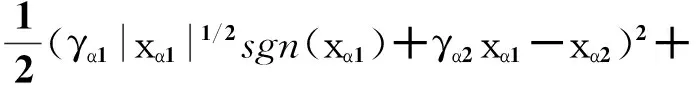
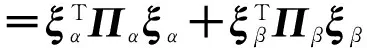
(9)

其中：

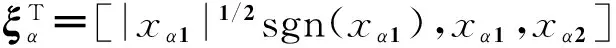
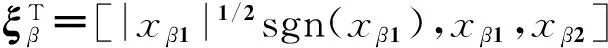
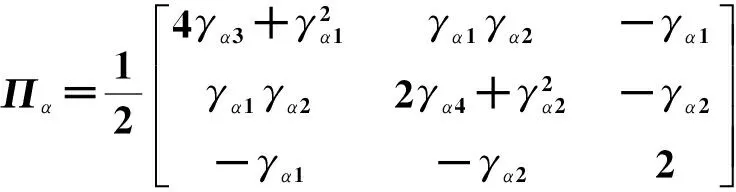
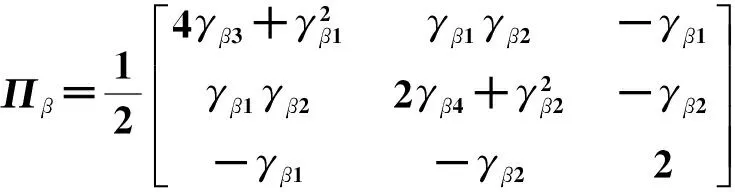
V(x)对时间的一阶导数为

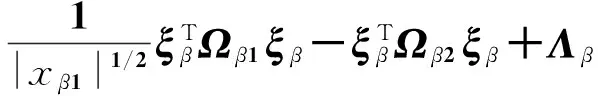
(10)

其中：

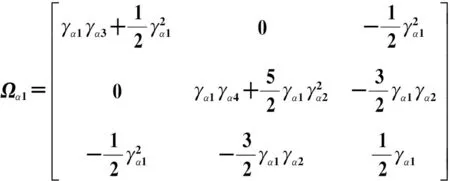
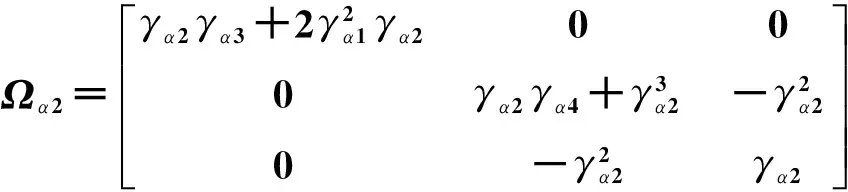
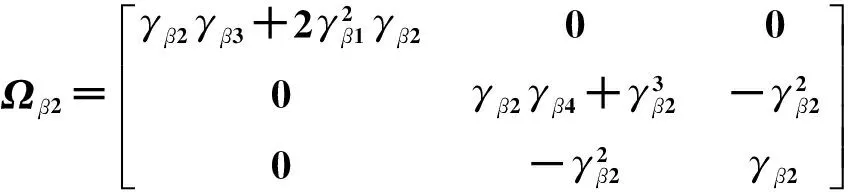
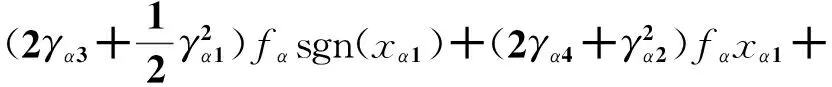
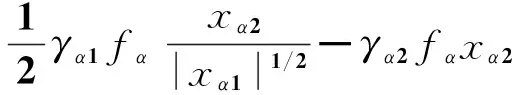
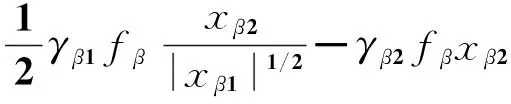
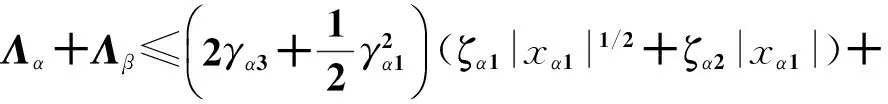
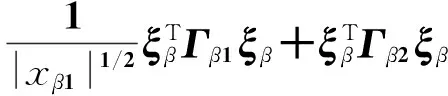
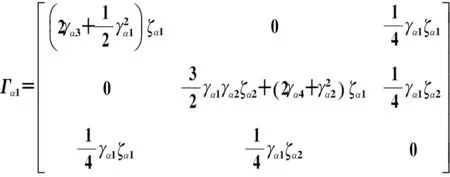
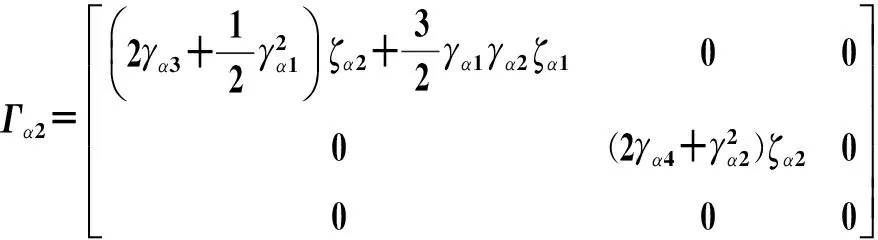
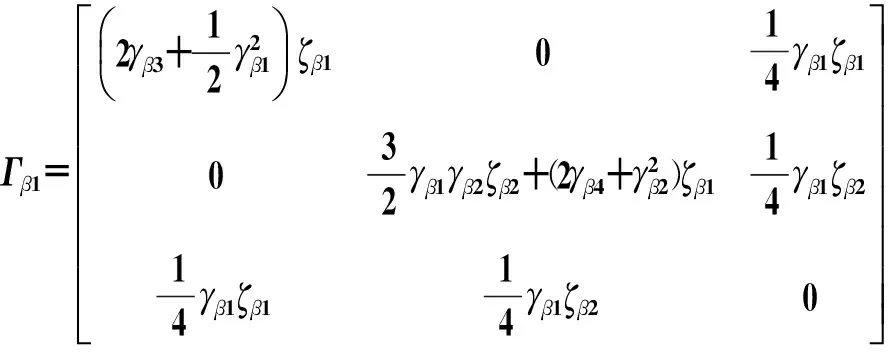
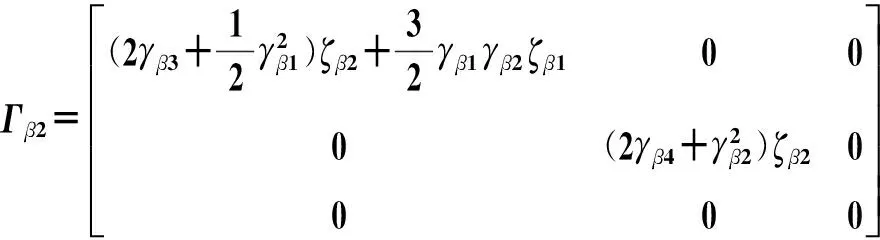
则

(11)

(Ωα1-Γα1)、(Ωα2-Γα2)、(Ωβ1-Γβ1)、(Ωβ2-Γβ2)为正定矩阵的条件如下：

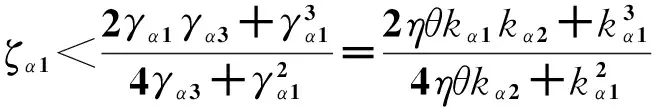
(12)

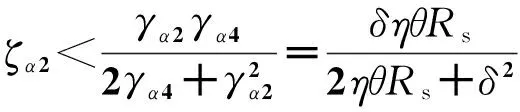
(13)

(14)

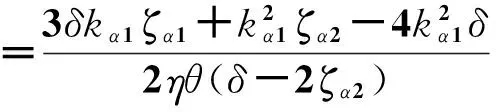
(16)

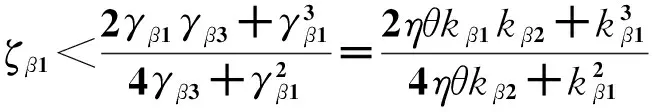
(17)

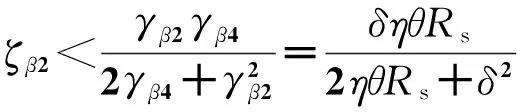
(18)

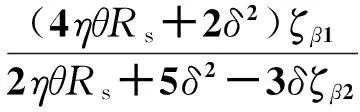
(19)

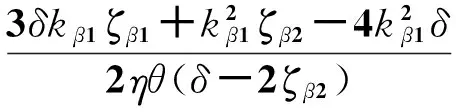
(20)

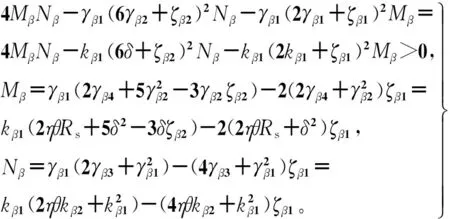
(21)

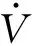
4仿真与实验验证

为了检验所设计的基于Super-twisting算法的感应电机定子磁链观测器的有效性，进行了Matlab仿真与实验。在仿真中将其与常规电压模型法定子磁链观测器进行了比较研究，常规定子磁链电压模型如图2所示。

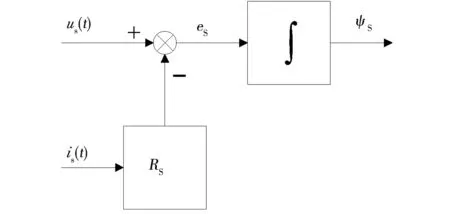
图2　定子磁链电压模型Fig.2　U-I model of stator flux

Matlab仿真中，定子磁链的实际值由电机的数学模型给出。电机参数为：额定电压UN=220V，定子电阻Rs=94Ω，转子电阻Rr=83.9Ω，定子自感Ls=5.387H，转子自感Lr=5.387H，互感Lm=5.082H，转动惯量J=0.105kg·m2。观测器控制参数为：kα1=kβ1=200(即γα1=γβ1=200)，kα2=kβ2=10(即γα3=γβ3=262.8)。

电机施加220V、15Hz的三相交流电，在开环下空载运转，4s时，施加3N·m负载转矩。仿真时间6s，仿真结果如图3～图5所示。

Super-twisting算法磁链估算误差稳定后在0.2范围内，如图4(c)所示；电压模型法磁链估算误差范围超过了0.6，如图4(d)所示。由此可以看出，基于Super-twisting算法的磁链观测器的估算误差比电压模型法的估算误差小。

定子电阻阻值发生变化时，电压模型法磁链估算会产生漂移，而基于Super-twisting算法的磁链观测器能够较好的抑制磁链漂移。

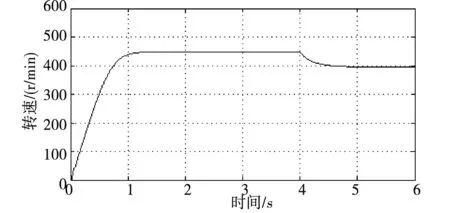
图3　电机转速Fig.3　Speed of motor

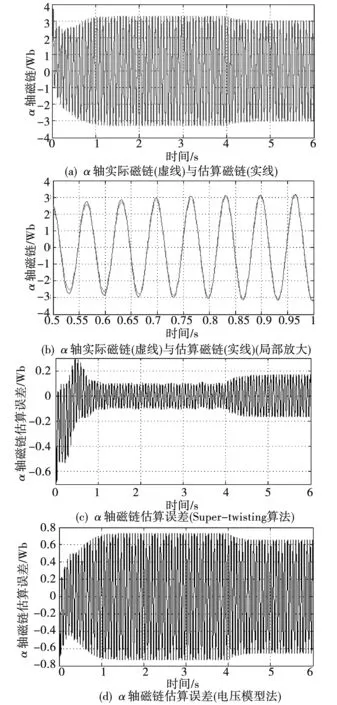
图4　α轴实际磁链与估算磁链Fig.4　Actual and estimated α axis flux

观测器模型及控制参数不变，定子电阻阻值变为原来的2倍(188Ω)，电机其它参数不变。电机施加220V、15Hz的三相交流电，在开环下空载运转，4s时，施加3N·m负载转矩。仿真结果如图5所示。

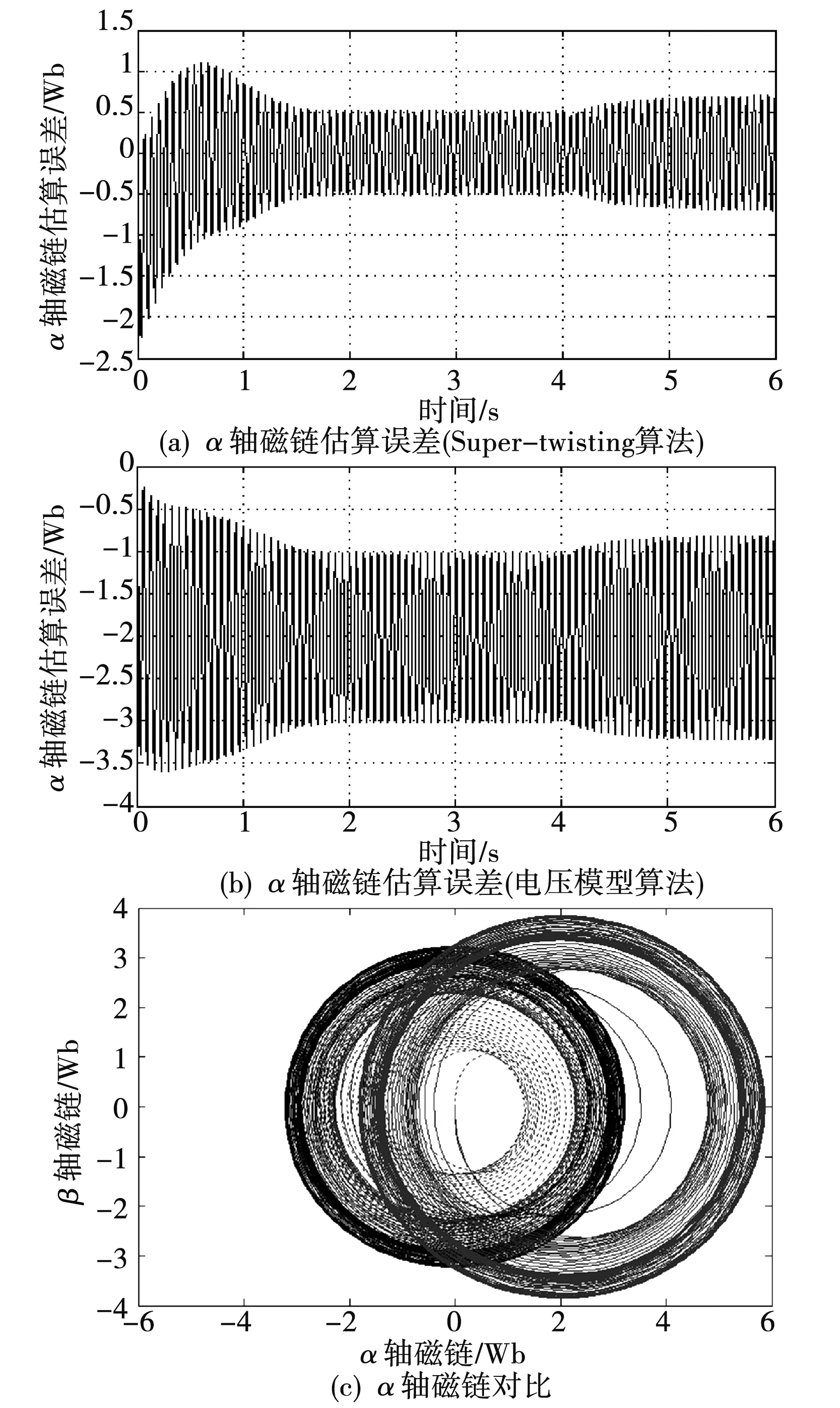
图5　定子电阻阻值改变时α轴磁链(Rs=188 Ω)Fig.5　　　　The estimated α axis flux when stator 　　　resistance is changed (Rs=188 Ω)

Super-twisting算法磁链观测器经过一段时间后，磁链误差稳定在-0.7～0.7之间，如图5(a)所示；而电压模型法磁链观测器磁链误差一直在-3.5～0.7之间，产生较大漂移，如图5(b)所示。从图5(c)(浅灰色虚线表示实际磁链，深黑色实线表示Super-twisting算法估算磁链，浅灰色实线表示电压模型法估算磁链)中也可以直观的看出，电压模型法磁链观测器估算磁链产生很大的漂移，而Super-twisting算法磁链观测器能够较好地观测磁链。因此对于定子电阻参数易变的电机来说，控制时是不能直接使用电压模型法来估算定子磁链的，可以考虑使用Super-twisting算法磁链观测器来估算磁链。

将Super-twisting算法定子观测器应用到感应电机直接转矩控制中，电机参数和定子磁链观测器控制参数与开环时一样，定子磁链给定值Ψ=1Wb，给定转速600r/min，转速调节器采用PID控制，其中比例系数KP=20，积分系数KI=0.01，微分系数KD=0.2。仿真时间20s，仿真结果如图6所示。

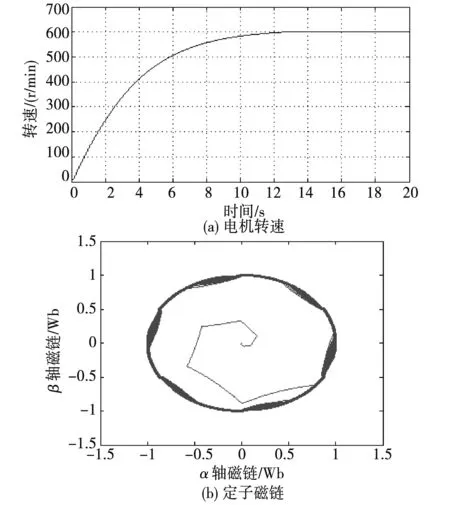
图6　　　　基于Super-twisting算法的定子磁链观测器　　　应用到感应电机直接转矩控制中(仿真结果)Fig.6　　　　Stator flux observer based on Super-twisting 　　　algorithm for direct torque control of 　　　induction motor (simulation results)

将“基于Super-twisting算法的定子磁链观测器”直接转矩控制与“基于电压模型法的定子磁链观测器”直接转矩控制进行对比，其输出电磁转矩如图7所示。从图7(a)中可以看出，Super-twisting算法输出转矩从高到低没有较大突变，同时从图7(b)可以看出，转矩变化频率比电压模型法更小。所以综合来说，Super-twisting算法输出转矩品质更高。

为了验证Super-twisting算法定子磁链观测器的实际可行性，利用“电力电子与电气传动综合实验台”进行实验。实验台组成包括：功率挂箱、主控挂箱、加载控制箱、电动机、上位机，如图8所示。实验电机为鼠笼式三相异步电动机，参数与仿真时所用电机参数相同。转速给定值600r/min，实验结果如图9所示。

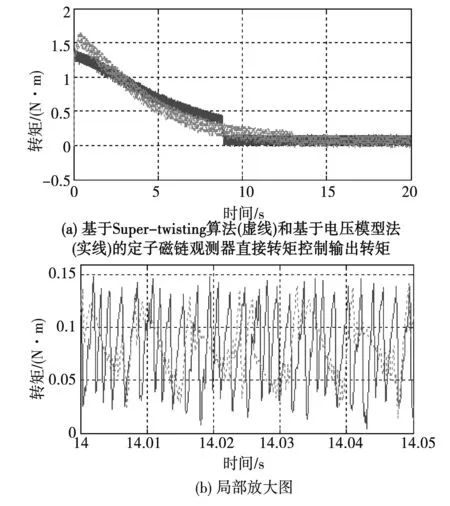
图7　感应电机直接转矩控制输出转矩(仿真结果)Fig.7　　　　The output torque of direct torque control of　　　 induction motor (simulation results)

图8　电力电子与电气传动综合实验台Fig.8　　　　Comprehensive experiment-bed of power　　　 electronics and electrical drives

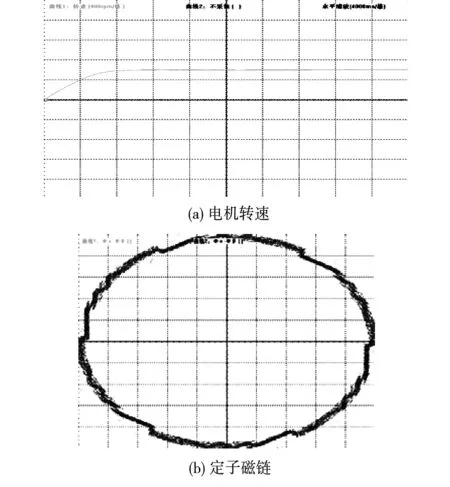
图9　　　　基于Super-twisting算法的定子磁链观测器　　　应用到感应电机直接转矩控制中(实验结果)Fig.9　　　　Stator flux observer based on Super-twisting 　　　algorithm for direct torque control of　　　 induction motor (experimental results)

从仿真和实验结果可以看出，Super-twisting算法定子磁链观测器能够很好的观测定子磁链，电机转速也最终稳定在了给定值600r/min，从而证明了基于Super-twisting算法的感应电机定子磁链观测器的实际可行性。

5结论

本文将Super-twisting算法应用于估算感应电机定子磁链，设计了一种基于Super-twisting算法的感应电机定子磁链观测器，并将此观测器应用到直接转矩控制中。在对观测器系统稳定性进行分析时，巧妙地将转速和耦合量当作扰动来处理，并给出了观测器系统稳定的约束条件。该方法利用滑模变结构控制的鲁棒性特点来抑制扰动，有效地提高了磁链观测精度，同时解决了定子电阻参数发生变化时磁链估算会产生漂移的问题。仿真和实验结果验证了这种方法的有效性和可行性。

参 考 文 献:

[1]PELLEGRINO G,GUGLIELMI P,ARMANDO E,et al.Self-commissioning algorithm for inverter nonlinearity compensation in sensorless induction motor drives[J].IEEE Transactions on Industry Applications,2010,46(4): 1416-1424.

[2]RODIC M,JEZERNIK K.Speed-sensorless sliding-mode torque control of an induction motor[J].IEEE Transactions on Industrial Electronics,2002,49(1): 87-95.

[3]张猛,肖曦,李永东.基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器[J].中国电机工程学报,2007,27(36): 36-40．

ZHANG Meng,XIAO Xi,LI Yongdong.Speed and flux linkage observer for permanent magnet synchronous motor based on EKF[J].Proceedings of the CSEE,2007,27(36):36-40.

[4]李红,罗裕,韩邦成,等.带通滤波器法电压积分型定子磁链观测器[J].电机与控制学报,2013,17(9):8-16.

LI Hong,LUO Yu,HAN Bangcheng,et al.Voltage integral model for stator flux estimator based on band-pass filter[J].Electric Machines and Control,2013,17(9):8-16.

[5]SPICHARTZ M,STEIMEL A.Stator-flux-oriented control with high torque dynamics in the whole speed range for electric vehicles [J].Emobility-Electrical Power Train,2010.IEEE,2010: 1-6.

[6]王丙元,冯辉.基于定子电流的模型参考自适应感应电机转速估计[J].电机与控制学报,2013,17(9): 48-56.

WANG Bingyuan,FENG Hui.Stator-current-based MRAS estimator for induction motors[J].Electric Machines and Control,2013,17(9):48-56.

[7]BARUT M,BOGOSYAN S,GOKASAN M.Speed-sensorless estimation for induction motors using extended Kalman filters[J].IEEE Transactions on Industrial Electronics,2007,54(1): 272-280.

[8]HAQUE M E,ZHONG L,RAHMAN M F.A sensorless initial rotor position estimation scheme for a direct torque controlled interior permanent magnet synchronous motor drive[J].IEEE Transactions on Power Electronics,2003,18(6): 1376-1383.

[9]SIMOES M G,BOSE B K.Neural network based estimation of feedback signals for a vector controlled induction motor drive[J].IEEE Transactions on Industry Applications,1995,31(3): 620-629.

[10]LI J C,XU L Y,ZHANG Z.An adaptive sliding-mode observer for induction motor sensorless speed control[J].IEEE Transactions on Industry Applications,2005,41(4): 1039-1046.

[11]REHMAN H.Elimination of the stator resistance sensitivity and voltage sensor requirement problems for DFO control of an induction machine[J].IEEE Transactions on Industrial Electronics,2005,52(1): 263-269.

[12]YOUNG K D,UTKIN V I,OZGUNER U.A control engineer's guide to sliding mode control[J].IEEE Transactions on Control Systems Technology,1999,7(3): 328-342.

[13]LEVANT A.Robust exact differentiation via sliding mode technique[J].Automatica,1998,34(3): 379-384.

[14]DAVILA J,FRIDMAN L,LEVANT A.Second-order sliding-mode observer for mechanical systems[J].IEEE Transactions on Automatic Control,2005,50(11): 1785-1789.

[15]MORENO J A,OSORIO M.A Lyapunov approach to second-order sliding mode controllers and observers[C]//Proceedings of the IEEE Conference on Decision and Control,2008,Cancun.2008: 2856-2861.

[16]李鹏.传统和高阶滑模控制研究及其应用[D].长沙：国防科学技术大学,2011.

(编辑：张楠)

Design of Super-twisting algorithm stator flux observer for induction motor

PAN Yue-dou1,2,CHEN Tao1,2，CHEN Ze-ping1,2

(1.School of Automation,University of Science and Technology Beijing,Beijing 100083,China; 2.Key Laboratory of Advanced Control of Iron and Steel Process (Ministry of Education),Beijing 100083,China)

Abstract:In order to improve the observation accuracy of stator flux of induction motor,a stator flux estimation method based on Super-twisting algorithm was proposed.A stator flux observer was designed and applied for direct torque control of induction motor.According to the robustness of sliding mode variable structure control,the disturbance of the multiple input multiple output stator flux observer system was restrained.By using the advantages of Super-twisting algorithm which require less information to design a simple control law,and thus more suitable for practical engineering applications.The speed and amount of coupling were regarded as disturbances in the analysis of the stability of observer,and the sufficient conditions of the system uniformly asymptotically stable was presented.Compared with the u-i model observer,the proposed observer based on Super-twisting algorithm is more accurate and has better robustness to the change of stator resistance.Simulation and experiment results validate the proposed method.

Keywords:induction motor; super-twisting algorithm; flux estimation; current estimation; direct torque control

收稿日期:2015-06-18

基金项目：国家自然科学基金(51331002)

作者简介：潘月斗(1966—)，男，博士，副教授，研究方向为电气传动及自动化；陈泽平(1989—)，男，硕士，研究方向为电气传动及自动化。

通讯作者:潘月斗

DOI:10.15938/j.emc.2016.05.009

中图分类号:TM 343

文献标志码:A

文章编号:1007-449X(2016)05-0060-08

陈涛(1991—)，男，硕士研究生，研究方向为电气传动及自动化；