全数字转差轴角变换器

马泽涛，　崔淑梅，　韩守亮，　侯晓宝

(1.哈尔滨工业大学 电气工程及自动化学院, 黑龙江 哈尔滨 150001；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266000)



全数字转差轴角变换器

马泽涛1，崔淑梅1，韩守亮1，侯晓宝2

(1.哈尔滨工业大学 电气工程及自动化学院, 黑龙江 哈尔滨 150001；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266000)

摘要:针对双转子电机在实现精确矢量控制时需要其内外转子的相对转速/相对转角信息的问题，提出一种基于旋转变压器测量双转子电机内外转子的相对转速/转角的方法。首先，基于坐标变换对旋转变压器的全数字轴角变换算法进行改进，设计一种全数字转差轴角变换算法，使改进后的算法可对相对转速/相对转角进行精确闭环跟踪，而且轴角变换算法的复杂度较直接求差获得相对转速/转角可以减少一半，使其易于实现。其次，通过仿真分析验证全数字转差轴角变换算法的正确性，并基于TMS320F2812设计相对转速/转角测量系统，进行相关的硬件设计和软件设计。最后，通过实验验证了所设计系统的可行性。

关键词:传感器；旋转变压器；轴角变换；坐标变换；相对转角

0引言

近年来，双转子电机被提出作为一种重要部件应用于混合动力汽车中[1-3]。双转子电机由于释放了定子，使其具有两个旋转部件，因此实现其矢量控制时往往要获得内外转子上机械转轴的相对转速/转角，即不同机械转轴间的转速差/转角差。目前，市场上并无成熟的转速差/转角差传感器出现[4]，因此，这种传感器的设计一般都是采用在不同机械转轴中安装现有转速/转角传感器的方法，对测量结果进行求差完成，此种方法属于开环计算方法，其精度及可靠性均有待提高[4-5]。其次，考虑到车用环境对传感器的可靠性要求苛刻以及受电机本身的结构所限制，双转子电机内转子和外转子转轴上所安装的转速/转角传感器多采用旋转变压器[6-8]，导致转速差/转角差的获得需要两套轴角变换器，系统复杂，成本高。若采用微处理器进行轴角变换器的设计，虽然可以降低硬件成本，但是在算法中，一次采样周期需要进行两次轴角变换，在目前的解码算法中，无论是采用反正切解码算法，还是锁相环闭环跟踪算法[10]，均需要进行三角函数的运算，计算量大，对微处理器的要求高，同样不利于降低成本。

本文基于旋转变压器的全数字轴角变换算法[11]，在双转子电机的内转子转轴和外转子转轴上分别安装旋转变压器，设计一种全数字转差轴角变换器，完成对转速差/转角差的闭环跟踪，以提高测量精度，并有效减少算法规模。

1基于全数字轴角变换算法的转差算法设计

1.1全数字轴角变换原理

设旋转变压器的输出信号为

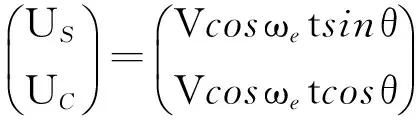
(1)

式中：US、UC分别为旋转变压器的正余弦绕组输出；V为信号幅值；ωe为激磁信号角频率；θ为机械转角。

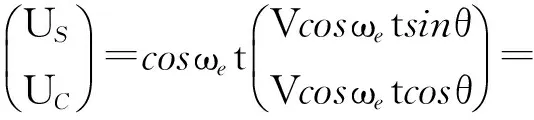
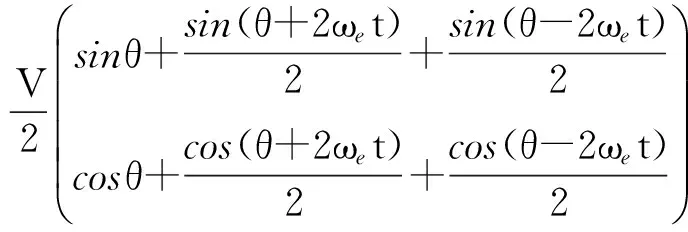
(2)

由式(2)可以看出，进行同步解调后，信号被分成包含位置角信息的低频分量和包含激磁信号频率的高频分量，同步解调前后的频谱如图1所示。

采用FIR数字滤波器对式(2)进行低通滤波后，即可得到仅包含位置角信息的正余弦分量，将其输入锁相环即可完成对位置角的闭环跟踪，并得到转速。

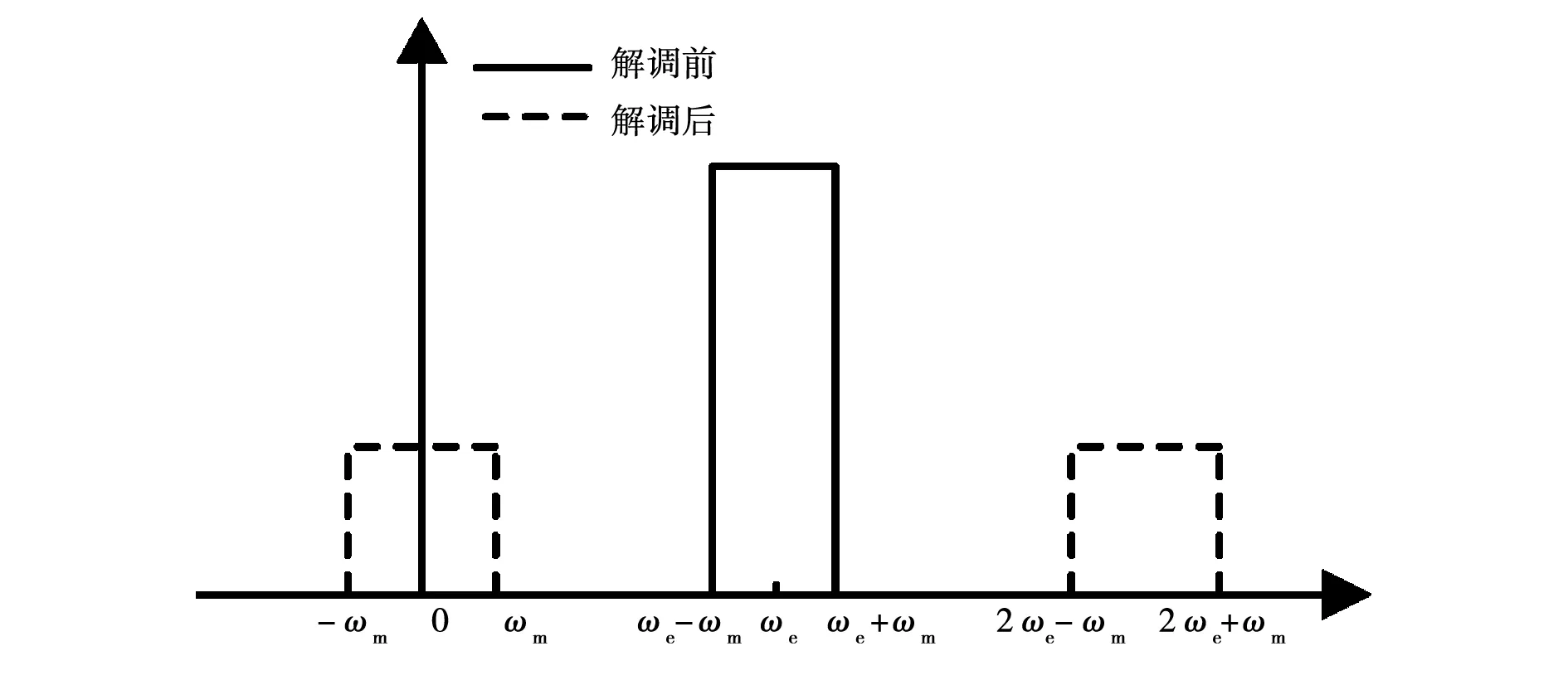
图1　同步解调前后信号频谱对比Fig.1　Signal spectrum comparison after demodulated

通常的轴角变换算法均采用在载波周期的极值点进行采样的方法，以达到较高的采样精度。然而从式(2)可以看出，旋转变压器的包含的信号分量中最高信号频率为θ+2ωet，即采用上述采样方法其采样频率小于其最大信号频率的两倍，因此属于欠采样，会使得信号中包含高次谐波，影响传感器精度。而全数字轴角变换器由于采用了同步解调技术，可以对信号进行过采样，即采用较高的采样频率(如数倍奈奎斯特频率)进行采样，从算法上提高了采样的精度，因此可以降低系统对ADC的要求，加之采用锁相环闭环跟踪技术，可以达到较高的轴角变换精度。

1.2全数字转差轴角变换器设计

基于以上的全数字轴角变换算法，对其进行改进设计，使其适用于转差测量。设在双转子电机内转子转轴上安装旋转变压器1，外转子转轴上安装旋转变压器2，内转子与外转子的机械转角分别为

(3)

而内转子与外转子之间的相对转角则定义为

Δθ=θ1-θ2=Δωt。

(4)

在本文中，将Δθ、Δω分别称为转角差，转速差，将二者统称为转差。

1.2.1基于坐标变换获得转差信息

令旋转变压器1与旋转变压器2采用相同的激磁信号，则其输出信号分别可以表示为

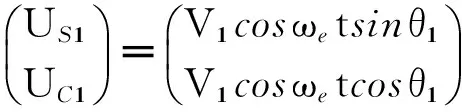
(5)

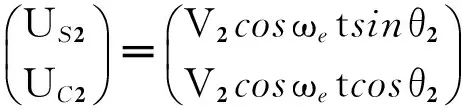
(6)

将旋转变压器2的输出信号作为旋转坐标系，将旋转变压器1的输出信号投影到旋转变压器2的输出信号上，即进行PARK变换，可以得到

(7)

式(7)中，USH、UCH为信号频移后的高频分量，满足

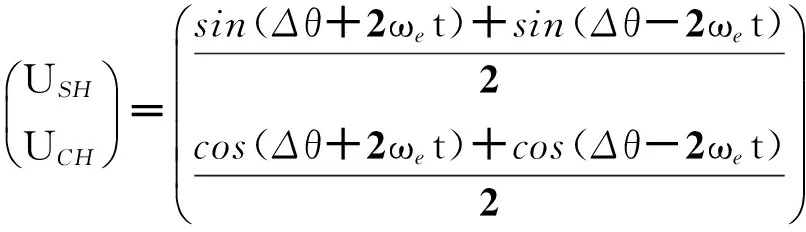
(8)

由于相对于激磁信号角频率ωe来说，通常Δω较小，故由式(7)可知，经过坐标变换后，不仅可以获得转差信息，还可以完成频谱搬移，将信号分成高频分量和低频分量。因此，只要将此信号通入FIR低通滤波器，即可完成解调，获得仅包含转差信息的正余弦分量。最终得到锁相环前端的两相正余弦输入信号如式(9)所示。

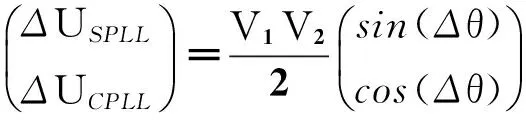
(9)

1.2.2转差闭环跟踪

为获得高精度的解算结果，采用锁相环对转差进行闭环跟踪。设解算输出的转角差为φ，转速差为Δωout，设计锁相环解算回路如图2所示。

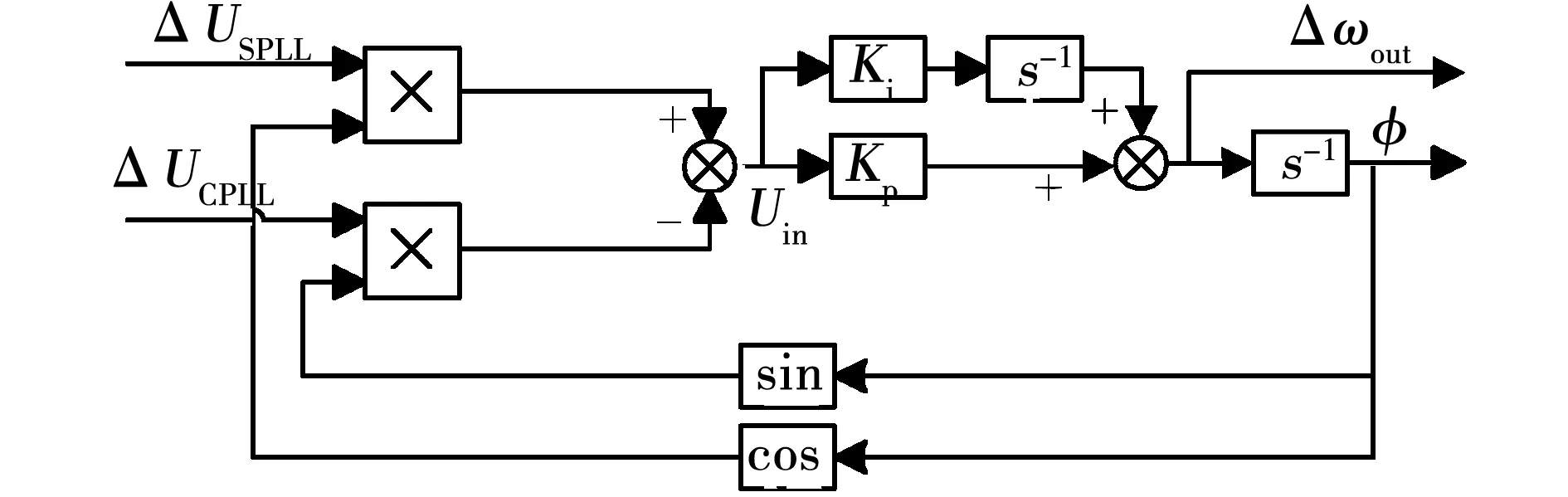
图2　锁相环闭环跟踪回路Fig.2　PLL tracking closed loop

锁相环本质上是一个二阶伺服系统，解算输出转角差φ与锁相环前端两相输入正余弦信号、锁相环输入信号Uin满足

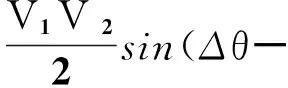
(10)

当锁相环环路跟踪完成锁相时，有

error=Δθ-φ≈sin(Δθ-φ)。

(11)

即

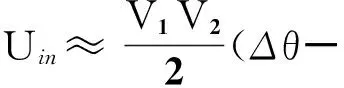
(12)

锁相环闭环回路传递函数为

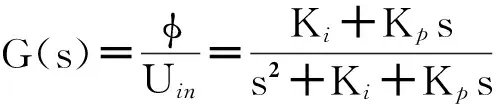
(13)

根据二阶闭环系统的设计方法即可以确定锁相环PI控制器的PI参数。

1.2.3相位滞后补偿

在所设计的全数字转差轴角变换算法中，应用FIR低通滤波器对式(7)进行滤波，以得到仅包含转差信息的低频分量。信号通过FIR低通滤波器后会产生相位滞后，影响轴角变换器的解算精度。

由于FIR低通滤波器具有线性相位特性，因此，在稳态下可以根据解算出的转速差对位置差进行完全补偿，补偿相位为

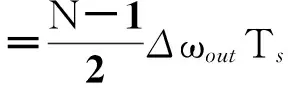
(14)

式中：N为FIR低通滤波器的除数；Ts为采样周期。

1.3全数字转差轴角变换算法与直接求差法的对比

基于全数字轴角变换器，直接对双转子电机内外转子的转角进行求差时，转差算法框图如图3所示；而基于全数字转差轴角变换算法获得转差时，算法框图如图4所示。

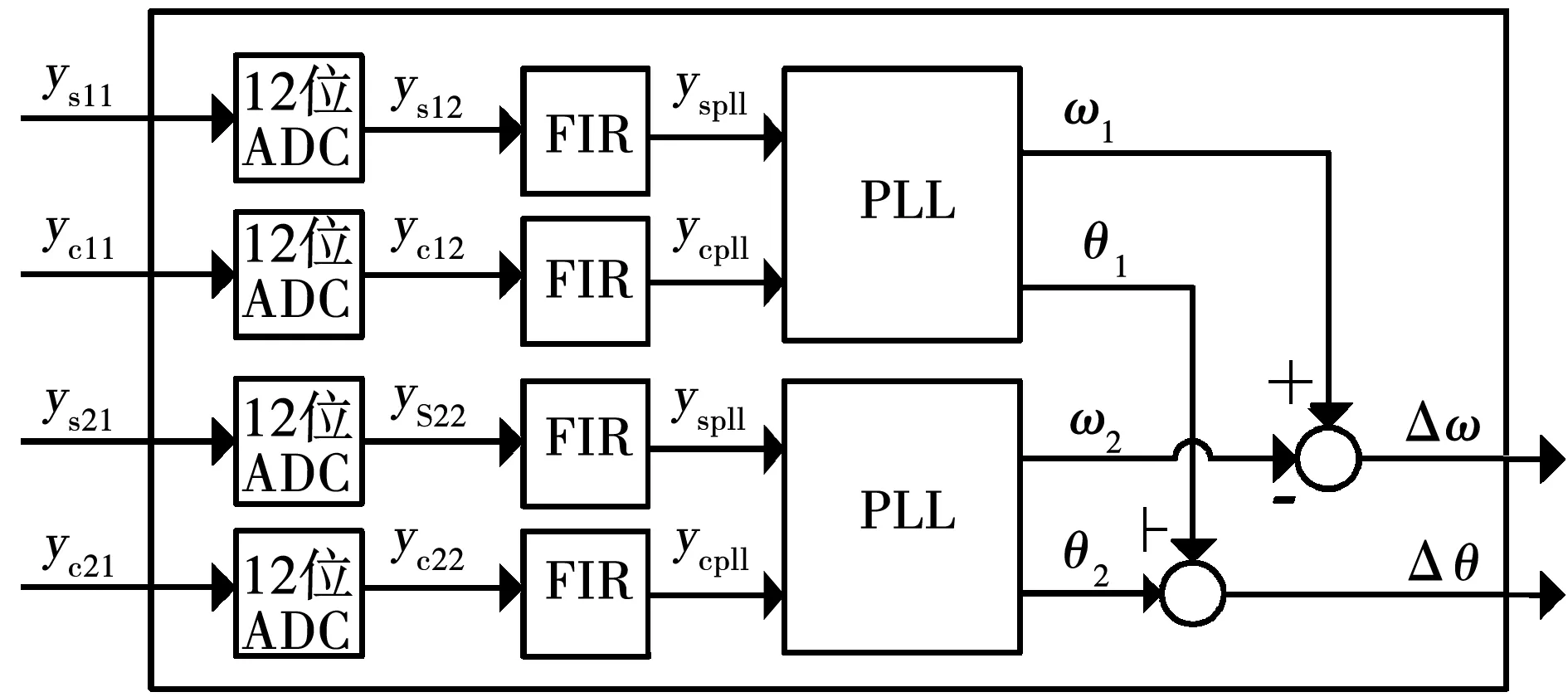
图3　直接求差法算法框图Fig.3　Algorithm diagram of open loop

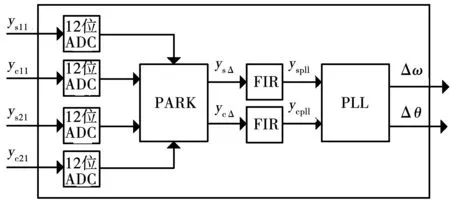
图4　全数字转差轴角变换算法框图Fig.4　　　　Algorithm of all digital R2D converter for　　　 angular position difference

对比图3和图4可以看出，由于PARK变换只涉及对信号的乘加运算，因此全数字转差轴角变换算法较直接求差法而言，算法的复杂度减少一半，有效减小了算法的复杂度，进而降低对微处理器的要求。另外，直接求差法属于开环算法，算法误差为两次轴角变换算法误差的叠加，而全数字转差轴角变换算法则是直接对转差进行闭环跟踪，因此后者测量结果更加精确。

2仿真分析

对本文所提出的全数字转差轴角变换算法进行仿真研究，验证算法的可行性。

利用Matlab对全数字转差轴角变换算法进行仿真研究，取激磁信号频率为10 KHz，旋转变压器输出信号幅值及轴角变换器输入信号幅值均为1 V，双转子电机内转子的转速为200π rad/s，外转子的转速为100π rad/s，解调部分采用128阶汉明窗FIR低通滤波器，仿真结果如图5所示。

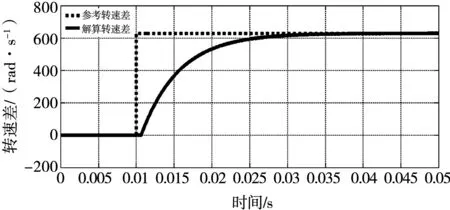
图5　转速差解算结果Fig.5　Calculation result of the speed difference

由图5可以看出，给定一阶跃转速差信号，转速差的解算结果与实际值相同，系统闭环跟踪响应快，解算精度高。但是位置差解算值较位置差实际值存在滞后,如图6所示。

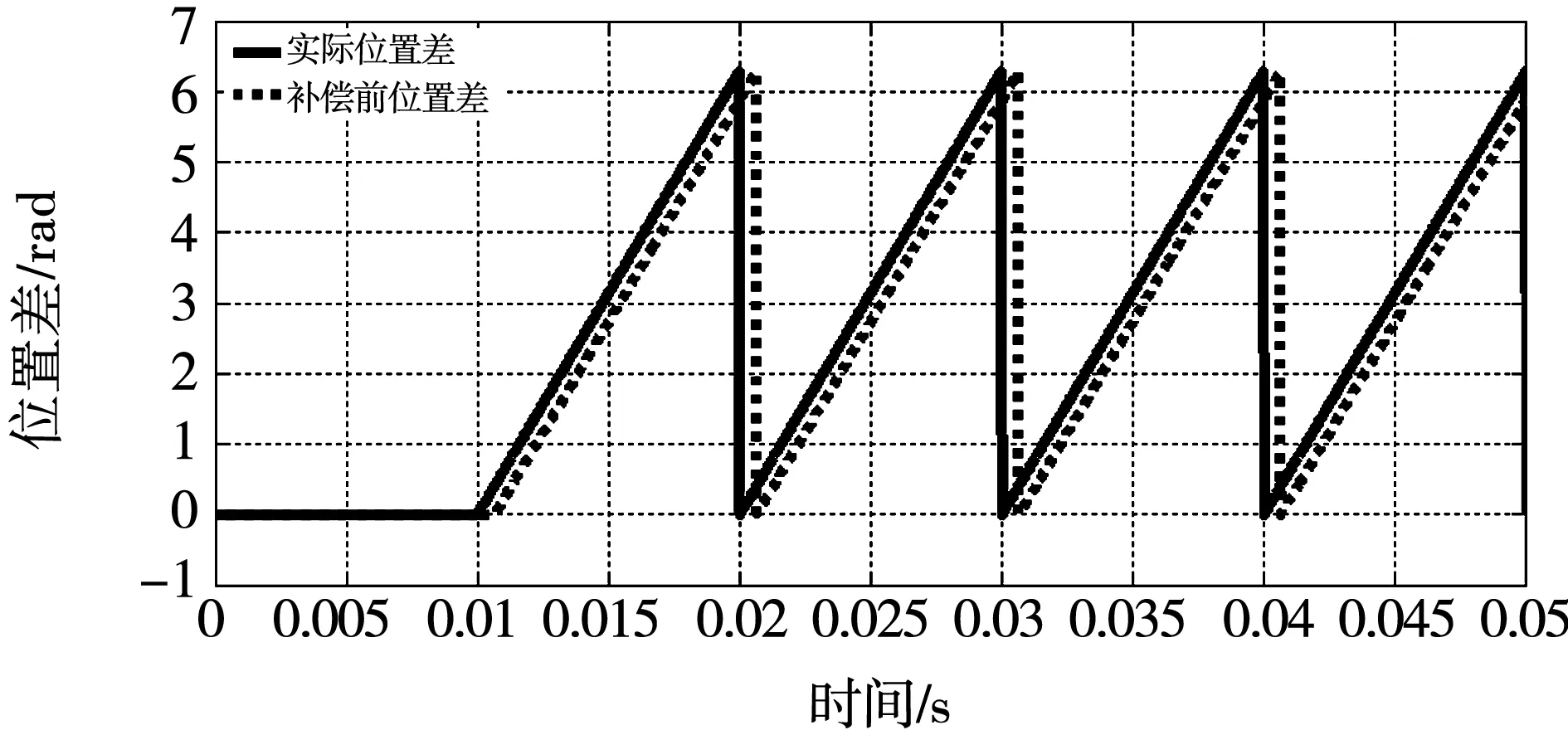
图6　补偿前位置差解算结果Fig.6　Calculation results before compensation

根据前面所设计相位滞后补偿公式，在全数字转差轴角变换算法中加入补偿环节，对其进行补偿后仿真，结果如图7所示，补偿后位置差的解算值与实际值可以完全重合。

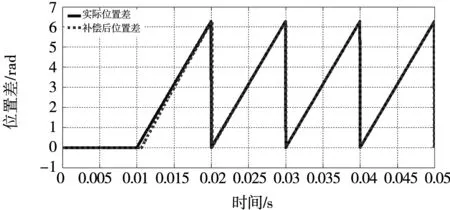
图7　补偿后位置差解算结果Fig.7　Calculation results after compensation

3转差测量系统设计与实验验证

3.1转差测量系统设计

基于TMS320F2812进行转差测量系统的设计。该转差测量系统应具有如下功能：1)生成高频正弦激磁信号作为旋转变压器输入；2)对旋转变压器一和二的共四路输出进行信号调理，并完成其ADC采样；3)对采样后的数据进行实时解算，完成转差的轴角变换，包括进行四路旋转变压器输出信号的PARK变换、对解调后的信号进行FIR滤波、对转差进行跟踪并对所解算出的位置角进行实时补偿；4)采用SPI串行通信输出转差结果。转差测量系统框图如图8所示。

3.1.1硬件设计

为提高整体电路的集成度并降低成本，本转差轴角变换器的硬件电路设计如下：

1)TMS320F2812进行查表后生成SPWM信号，经低通滤波后产生正弦激磁信号，由于旋转变压器要求输入平均值为零的交流信号，因此，需要对该正弦信号进行偏置，另外，为保证旋转变压器能正常工作，激磁信号应有一定的驱动能力，因此，需要对信号进行功率放大。本设计中，为简化系统设计，采用LM353运算放大器对SPWM输出信号进行放大偏置，而采用TCA0372功率运放进行扩流。2)通过4路ADC对旋转变压器一和旋转变压器二的输出信号进行采样，由于旋转变压器的输出信号为交流信号，信号幅值与激磁信号、旋转变压器变比有关，因此，一般需要将旋转变压器的输出进行直流偏置放大。对于每一路输出信号，均采用AD620仪用放大器进行偏置放大，可以简化外围电路的设计，并提高信号调理的精度，保证每对输出信号调理后的幅值偏差和相位偏差在误差设计范围内。AD620将旋变输出的交流信号偏置为直流信号时，需要稳定的基准电压，本设计中，选择MAX6168产生1.8 V的基准源。同时，由于TMS320F2812的ADC采样精度对于一个传感器系统来说稳定性较差，通常需要外扩昂贵的ADC芯片，在这里，为了节约成本，采用DSP2812的ADC采样结合AD校正的方式提高采样精度，为进行AD校正，需要两路稳定的直流基准，可以采用精密电阻对MAX6168所产生的1.8 V基准电压进行分压得到。3)采用DSP的SPI串行通信接口，为兼容TTL电平输出，采用SPI电平转换芯片。

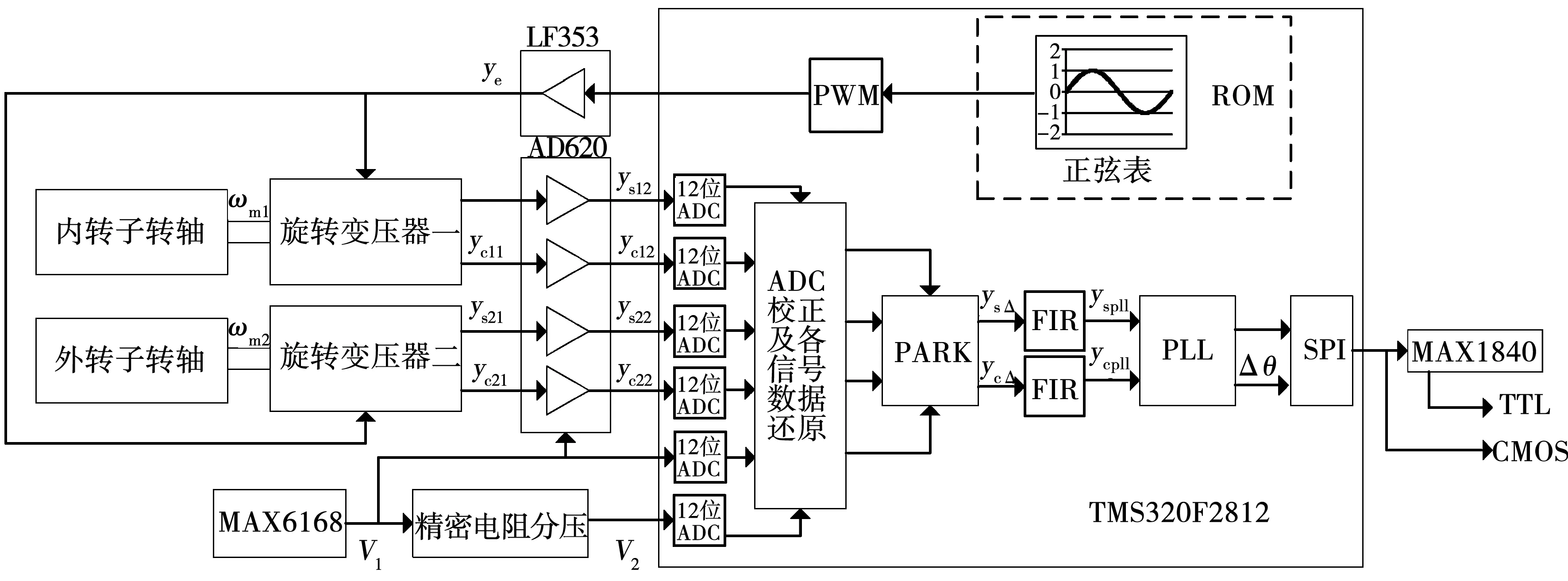
图8　基于TMS320F2812的转差测量系统框图Fig.8　System diagram of the converter

3.1.2软件设计

全数字转差轴角变换器的软件主要包括正余弦载波的生成和转差轴角变换算法，基于全数字转差轴角变换器的转差测量系统程序流程图如图9所示，程序执行过程如下所述。

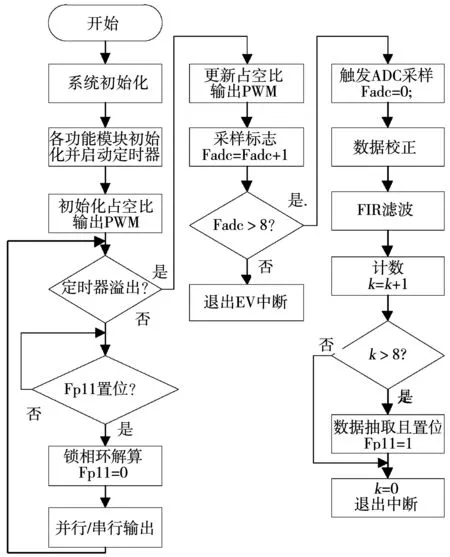
图9　全数字转差轴角变换算法流程图Fig.9　Chart of the all digital R2D converter

1)利用TMS320F2812的EV单元产生SPWM，并产生周期中断，进入中断后，对采样标志Fadc进行加计数，当Fadc计数到某一个值后，触发ADC采样。2)ADC采样完毕后进入采样中断，在该中断子程序中由两路基准信号对两套旋转变压器的四路信号进行线性校正，校正后完成对数据的还原，并进行PARK变换和FIR滤波运算，为提高FIR运算速度，采用TI公司提供的32位定点FIR汇编算法，由于采用了过采样技术，在该子程序中还应完成对数据的抽取，因此设置抽取计数，当加计数至某个值后完成数据抽取，并置位解算标志。3)在主程序中，查询解算标志，当解算标志置位时，完成一次解算，并将结果由SPI串行输出。

3.2转差测量系统实验验证

实验中采用两台多摩川旋转变压器，其变比为0.23。由TMS320F2812产生10 kHz的正弦波，经偏置放大后信号峰峰值为8 V；由于AD620的输入偏置电压为1.8 V基准电压，因此旋转变压器输出信号经AD620仪用运放调理至0.88 V～2.72 V，符合采样输入要求；另外，1.8 V的基准电压经过精密电阻分压后，得到两路直流基准电压，由2812对其进行采样，以作为ADC线性校正的基准。所设计系统中，SPWM开关频率为160 kHz，采样频率为80 kHz，因此过采样率为4，每进行8次采样和FIR滤波处理后，进行一次锁相环解算，并更新解算结果。

1)当机械转轴一以300 r/min的角速度正向旋转，机械转轴二静止时，实验结果如图10所示。实验表明，解算结果相对机械转轴一的零角度位置有一相位差，此相位差即为机械转轴二静止时相对机械转轴一位于零角度位置时的转角差。

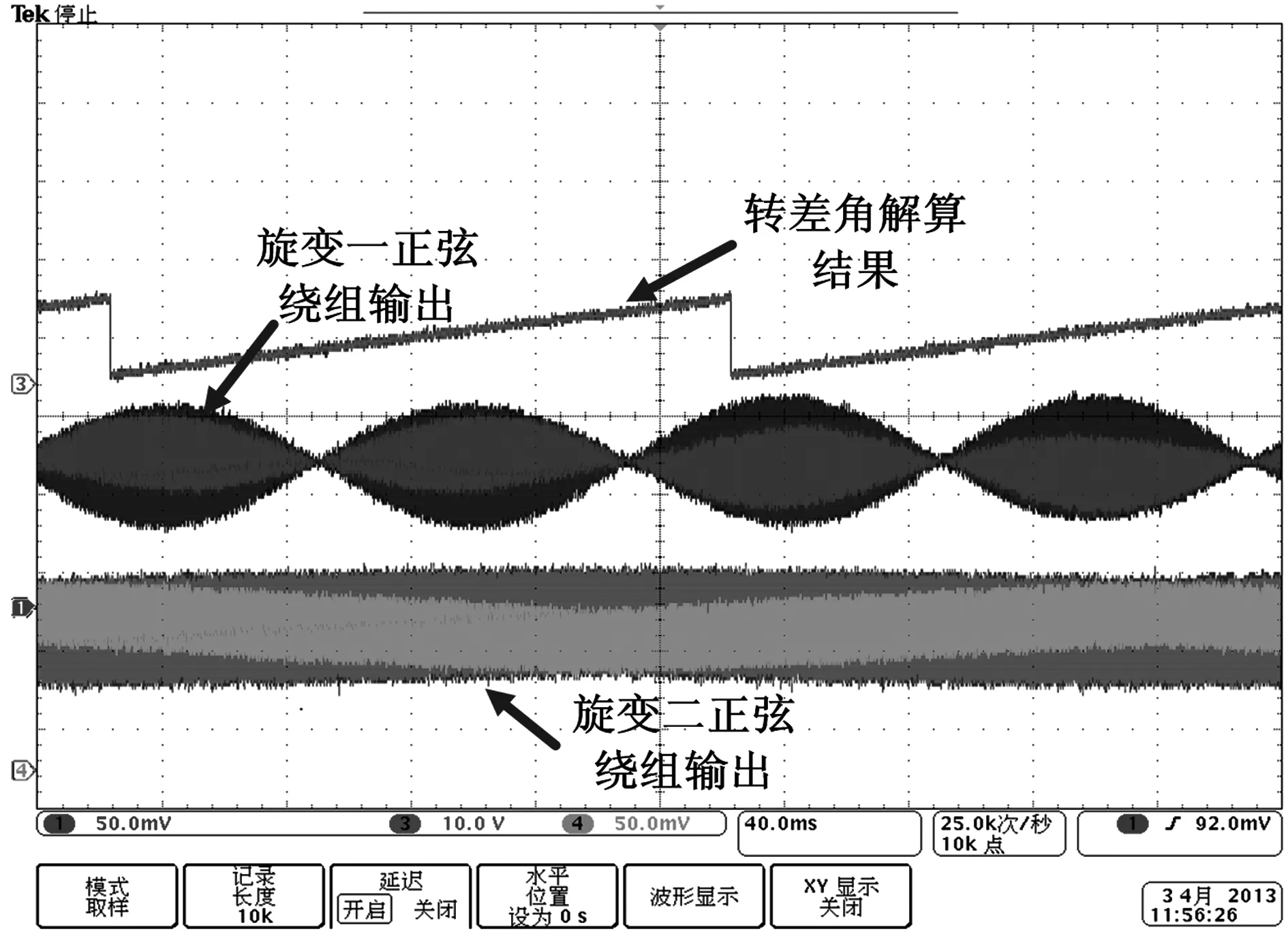
图10　机械转轴一300 r/min，机械转轴二静止Fig.10　　　　Rotating speed of axle1 is 300 r/min while　　　 the axle2 is stationery

2)当机械转轴一以300 r/min的速度旋转正向旋转，机械转轴二以200 r/min反向旋转时，实验结果如图11所示。解算结果显示，机械转轴一与机械转轴二的相对转速为500 r/min，与实际相符。

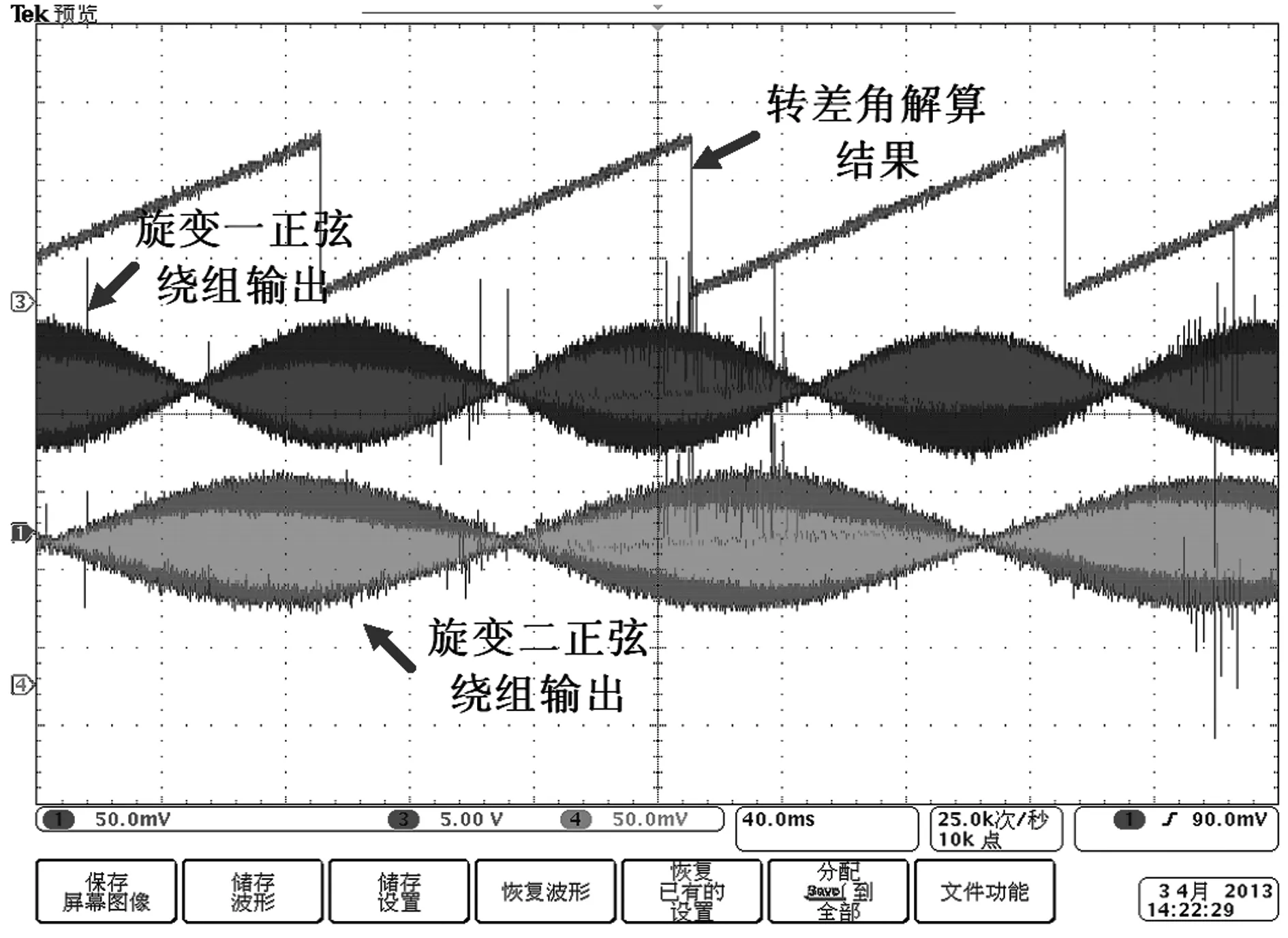
图11　机械转轴一300 r/min，机械转轴二-200 r/minFig.11　　　　Rotating speed of axle1 is 300 r/min and 　　　the axle2 is -200 r/min

4结论

本文提出了一种基于旋转变压器测量相对转角的方法，设计了一种全数字转差轴角变换算法，该算法的复杂度与解算绝对位置时的轴角变换算法相同，因此，与直接求差法测量相对转角相比，其计算量减少一半，且该算法可以实现对转差的闭环跟踪，因此提高了轴角变换器的可靠性。其次，进行了仿真分析，验证了算法的正确性。最后，进行了转差测量系统设计，包括其硬件设计和软件设计，并通过实验验证了算法的可行性。

参 考 文 献:

[1]HOEIJMAKERS M J,FERREIRA J A.The electrical variable transmission[C]//Conference Record of the IEEE Industry Applications Conference, Seattle, USA.2004, 4:2770-2777.

[2]HOEIJMAKERS M J.Electromechanical Converter[P]. U. S. Patent:WO 03/075437 A1, 2003: 1-16.

[3]崔淑梅, 程远, 陈清泉. 先进汽车电气变速器[J].电工技术学报,2006, 21(10): 111-116.

CUI Shumei, CHENG Yuan, CHEN Qingquan. An advanced electrical variable transmission for automobiles[J]. Transactions of China Electrotechnical Society，2006, 21(10): 111-116.

[4]徐奇伟,朱显辉,崔淑梅. 四端口机电能量变换器关键技术研究进展[J]. 电力电子技术,2011,45(12):17-19.

XU Qiwei, ZHU Xianhui, CUI Shumei. The key technology research progress of four ports electromechanical converter[J]. Power Electronics, 2011,45(12):17-19.

[5]佟诚德. 电动车用复合结构永磁同步电机控制系统的研究[M].哈尔滨：哈尔滨工业大学电气及其自动化系, 2009.

[6]SUN Lizhi.Analysis and improvement on the structure of variable reluctance resolvers[J]. IEEE Transactions on Magnetics, 2008,44(8):2002-2008.

[7]黄文祥. HEV用四端口机电能量变换器耦合问题的研究[D].哈尔滨：哈尔滨工业大学电气工程及自动化学院，2011.

[8]赵佳蓉, 李文韬, 黄苏融. 电动汽车用磁阻式旋变及其解码电路的协同仿真[J]. 电机与控制应用,2010,37(8):19-22.

ZHAO Jiarong, LI Wentao, HUANG Surong. Variable-reluctance resolver co-simulation with RDC for electrical vehicles[J]. Electric Machines & Control Application, 2010,37(8):19-22.

[9]李文韬，黄苏融. 车用电机系统磁阻式旋变转子设计与分析[J]. 电机与控制应用,2008，35(5):6-10.

LI Wentao, HUANG Surong. Rotor shape design and analysis of variable-reluctance resolver for hybrid-vehicle motor drive applications[J]. Electric Machines & Control Application, 2008，35(5):6-10.

[10]SANTANU Sarma,AGRAWAL V K,SUBRAMANYA Udupa.Software-based resolver-to-digital conversion using a DSP[J]. IEEE Transactions on Industrial Electronics, 2008,55(1): 371-379.

[11]JOAN Bergas-Jané,COIA Ferrater-Simón,GABRIEL Gross.High-accuracy all-digital resolver-to-digital conversion[J]. IEEE Transactions on Industrial Electronics, 2012,59(1):326-336.

(编辑：刘琳琳)

Research on all digital R2D converter for angular position difference

MA Ze-tao1，CUI Shu-mei1，HAN Shou-liang1，HOU Xiao-bao2

(1.Schoolof Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China; 2. CRRC QINGDAO SIFANG CO. LDT, Qingdao 266000, China)

Abstract:For realizing vector control on the double-rotor-machine, it is necessary to acquire the relative angular speed/position between the inner rotor and the outer rotor. A method for measuring the relative angular speed /position based on resolvers was put forward. Firstly, based on the transformation of coordinates, the all-digital R2D algorithm was improved to close-loop track the relative angular speed/position between two different rotors while the complexity of the algorithm is not increased, which made the converter easily realized. Secondly, simulation was done to prove the correctness of this algorithm, and then a measure system was designed based on TMS320F2812, including its hardware and software. Finally, experiment was finished to prove the reliability of this system.

Keywords:sensor; resolver; resolver-to- digital; coordinates transformation; relative angular position

收稿日期:2013-04-05

基金项目：国家自然科学基金(51277039)；国家科技支撑计划项目(2013BAG05B00)

作者简介：马泽涛(1988—)，男，博士研究生，研究方向为新能源汽车整车及电机控制；崔淑梅(1964—)，女，博士，教授，博士生导师，研究方向为新能源及电机与电机控制；韩守亮(1983—)，男，博士后，研究方向为电机优化设计；侯晓宝(1984—)，男，工程师，研究方向为动车组电气技术。

通讯作者:崔淑梅

DOI:10.15938/j.emc.2016.05.001

中图分类号:TM 383.2

文献标志码:A

文章编号:1007-449X(2016)05-0001-06