横向磁场永磁直线电机连续往复运行时温度场计算与分析

2016-06-13赵玫邹继斌张云亮韩辅君杨洪勇

电机与控制学报 2016年5期

赵玫,　邹继斌,　张云亮,　韩辅君,　杨洪勇

(1.鲁东大学信息与电气工程学院，山东烟台 264025；2.哈尔滨工业大学电气工程及其自动化学院，黑龙江哈尔滨 150001；3.威海广泰空港设备股份有限公司博士后科研工作站，山东威海 264200)

赵玫1,2,3,邹继斌2,张云亮3,韩辅君1,杨洪勇1

摘要:根据横向磁场永磁直线电机在直线运动系统中的具体应用，对连续往复运行工况下电机的温升特性进行了研究。在综合考虑电机结构和运行状态特殊性的基础上，首先，建立横向磁场永磁直线电机包含机壳端盖在内且计及电枢绕组三维结构的温度场计算模型；其次，应用传热学理论，在考虑电机热源、工作状态和电机各部分热交换等因素的前提下，给出电机中材料的热传导系数、比热容以及各个表面散热系数的确定方法，同时，给出动子表面的散热系数、气隙间动子外表面和定子内表面的散热系数随速度的变化规律；最后，计算电机在连续往复运行工况下的瞬态温度场，并通过样机实验对温度场的计算结果进行了验证。

关键词:横向磁场；永磁直线电机；温度场；连续往复

0引言

圆筒型直线电机常常被用于短行程的往复运动场合。随着它的应用场合越来越广泛，单机容量不断上升，它的发热和冷却问题也就越来越突出，并且电机的技术性能指标与热特性密切相关，良好的热设计可以最大限度的提高电机的技术性能指标，因此对其温度场的分析计算也就显得尤为重要。而本文所研究的横向磁场永磁直线电机属于圆筒型永磁直线电机(PMLM)，一方面由于其结构形式特殊，属于长动子短定子结构，定子铁心沿轴向多段排列，且铁心之间通过非导磁环连接，电枢绕组绕制方向平行于电机的运动方向，因此其温度场求解域模型有别于传统直线电机，需要建立其三维温度场计算模型。另一方面当直线电机的动子在连续变速往复运动时，气隙位置随动子的运动而改变，有别于传统旋转电机气隙结构不变的特点，因此动子各表面散热系数需要视流体的流动状态来确定。因此结合结构和运行特点对横向磁场圆筒型PMLM的温度场进行深入研究是十分必要的。

目前，关于本文所研究的横向磁场圆筒型直线电机的温度场研究还未有报道。因此，温度场方面的研究现状这里只能参考国内外传统直线电机的温度场研究[1-6]。对于圆筒型直线电机无非有两种结构形式：长动子短定子和长定子短动子。两种电机结构上的差异，导致在温度场计算方面也有所区别。文献[1]针对一种长定子短动子圆筒型直线电机，根据电机不同的工况选取不同的温度场计算域进行研究，运用有限元法建立了二维等效计算模型，以及给出了等效对流换热系数的确定方法。文献[2]将圆筒型直线感应电动机温度场作轴对称场处理，选取电机子午面(RZ截面)作为计算域，采用时步网络拓扑法计算其动态温度场；文献[3]选取定子和动子耦合区域的1/2作为温度场计算模型，计算了扁平型直线异步电机静止时的温升规律，由于电机实际运行过程中，动子表面及气隙内空气流动，以及动子和定子相对位置均会发生改变，因此文献所用静止法计算直线电机的温升在估算各种工况下电机温升时具有很大局限性；文献[4]选取电磁弹射用长行程大推力直线电机的初级作为温度场计算域，计算了绕组的温升规律；文献[5]在流体场计算基础上得到动子各表面的对流换热系数，并建立了简化的一维热路模型，该文献为直线电机表面对流换热系数的计算提供了指导，但是将复杂的电机热传导及热交换简化为一维热路，需要进行大量的理想假设。文献[6]采用电磁场——温度场耦合的方式来计算分析圆筒型永磁直线电机的电磁性能和温升问题，并通过实验进行了验证。

综上所述，关于直线电机温度场方面的研究主要集中在对电机温度场计算模型的等效处理，动子各表面对流换热系数的确定以及针对电机不同工况的温升预估等方面。而本文综合考虑了横向磁场圆筒型PMLM结构和运行状态的特殊性，建立其三维温度场计算模型。应用传热学理论，在考虑电机热源、工作状态和电机各部分的热交换等因素的前提下，详细讨论电机中材料的导热系数、比热容以及各个表面散热系数的确定方法，在此基础上对横向磁场圆筒型PMLM的瞬态温度场进行计算。根据电机在直线伺服系统中的具体应用，对连续往复运行工况下电机的温升特性进行分析和温升预估。

1横向磁场PMLM三维暂态温度场的计算模型

1.1数学模型

根据传热学理论，横向磁场圆筒型PMLM三维暂态温度场满足以下方程[7]：

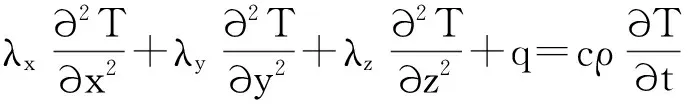
(1)

(2)

式中:T为温度(℃)；Ts为已知壁面温度(℃)；Tc为周围介质的温度(℃)；q为热源密度(W/m3)；q0为通过边界面的热流密度(W/m3)；c为比热容(J/(kg·℃))；ρ为密度(kg/m3)；t为时间(s)；h为散热系数(W/(m2·℃))；Si(i=1,2,3) 为第i类边界条件的物体边界；λn为边界面的法向导热系数(W/(m·℃))；λx、λy、λz为各介质x、y、z方向的导热系数(W/(m·℃))。

1.2基本假设和边界条件

电机温度场数值计算中，确定求解域是计算温度场的首要任务。本文所研究的横向磁场圆筒型PMLM属于长动子短定子结构，其电枢绕组的绕制方向平行于电机的运动方向，在确定温度场求解域时也有别于传统直线电机，不能单纯的只考虑定子和动子相耦合的区域，需要建立包含机壳端盖在内且计及电枢绕组的三维结构的温度场模型，此时的二维计算模型已不再适用，需要建立三维温度场计算模型，为了在保证计算准确度的前提下减少计算时间，对温度场计算模型的基本假设如下：

1)对于电机温度场定解问题的研究，不存在第一类边界；

2)电机中热源随温度的变化忽略不计；

3)机械损耗忽略不计；

4)材料属性随温度的变化忽略不计。

图1　横向磁场圆筒型PMLM三维温度场的求解区域Fig.1　　　　3D temperature field solved region in transverse　　　 flux tubular PMLM

图2　三维温度场求解区域的整体网格剖分图Fig.2　　　　3D whole mesh plot of the temperature field　　　 solved region

根据上述基本假设，计算区域内的传热和散热边界条件如图3所示，具体说明如下：

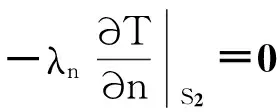
(3)

2)机壳外表面S1、前端盖外表面S2及后端盖外表面S4、绕组端部表面S7、动子左右上下表面S13、S16及轴的左右表面S12、定子铁心端面S10、定子齿冠表面S11、动子气隙间外表面S17面应用第三类对流换热边界条件，即满足如下边界条件

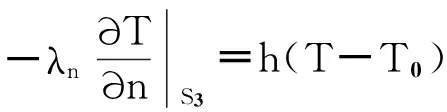
(4)

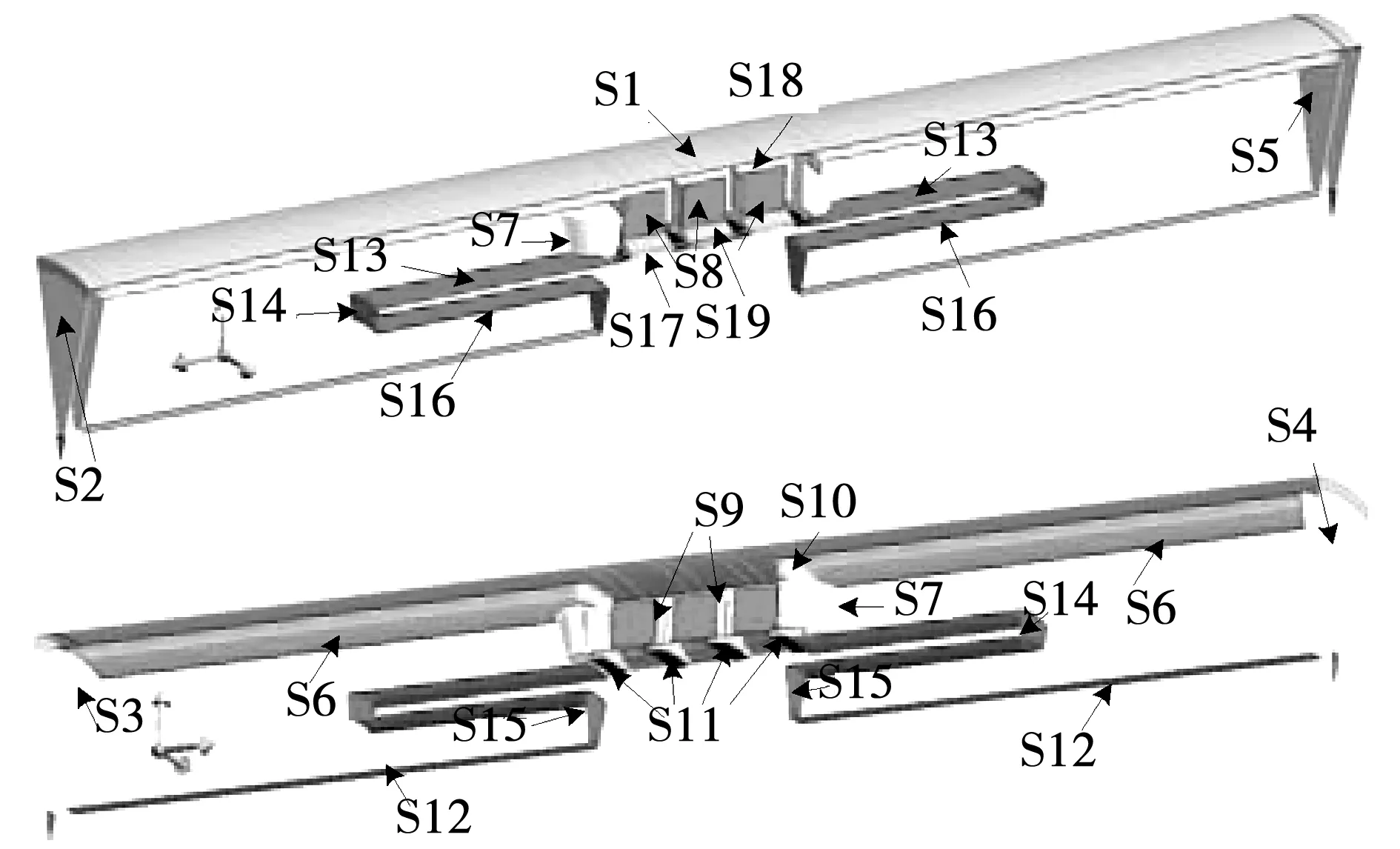
S1-机壳外表面；S2-前端盖外表面；S3-前端盖内表面；S4-后端盖外表面；S5-后端盖内表面；S6-机壳内表面；S7-端部绕组外表面；S8-绝缘层表面；S9-分段铁心外表面；S10-铁心端部外表面；S11-定子齿冠内表面；S12-轴表面；S13-动子上表面；S14-动子端部表面；S15-动子轭端部表面；S16-动子下表面；S17-气隙间动子外表面；S18-铝环内表面；S19-槽楔。图3　温度场求解域内散热面示意图Fig.3　　　　Schematic diagram of heat dissipation surface 　　　in the soved region

2热源的分布和热参数的确定

2.1热源的分布

电机在机电能量转换的过程中，其内部难免会产生铜耗、铁耗、涡流损耗、机械损耗和杂散损耗等各种损耗，这些损耗将转变成热能散发到电机周围的冷却介质中，同时也使电机的温度升高。我们通常把这部分使电机发热的损耗统称为热源。关于本电机的铜耗、铁耗和涡流损耗在文献[8]中做了详细研究，而由机械损耗所产生的热源在本文的温度场计算中忽略不计。

2.2热传导系数

根据傅里叶导热定律，热传导系数与物质的种类和温度等因素有关，是温度场计算中较重要的一个物理量，直接关系到物体内热流的大小[9]。横向磁场圆筒型PMLM的求解域中存在多种导热体，有铁心叠片、绕组铜线、槽绝缘、槽楔、隔磁铝环、永磁体、动子轭、轴，从导热材料与结构上主要分为各向同性和各向异性两种媒质。这些材料的系数可参考传统旋转电机的热传导系数的计算方法来确定[10]。

2.3表面散热系数

在电机中流体与固体壁面间的对流换热有很重要的实际意义，对流换热的强度关系到电机的温升及寿命。由于换热过程复杂，因此表征换热能力的表面散热系数与流体运动的性质、运动速度和固体表面的形状以及流体的物理性质等均有关系[11-14]。由于所研究的对象为长动子短定子圆筒型直线电机，电机空腔里存在多种对流换热现象，因此散热系数的选取也有所不同，考虑电机采用的是自然通风的冷却方式，可以根据流体具体的流动起因选择相似的实验关联式来得到不同的表面散热系数。

2.3.1自然对流表面散热系数的确定

在自然对流传热规律中，不同流动形态对应不同的关联式，本文采用近年来常用的格拉晓夫数Gr作为判定自然对流时流动形态转变的判据[14]。从物理意义上讲，格拉晓夫数Gr是浮生力和粘滞力的比值，且表达式为

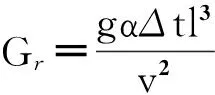
(5)

式中:g为重力加速度(m/s2)；α为空气的体胀系数，α=1/T，(K-1)；l为对于竖平板竖圆柱代表长度，对于横圆柱代表外径(m)；Δt为过余温度(℃)；v为动力粘度(m2/s)；T为定性温度即平均温度(℃)。

通过格拉晓夫数Gr的取值范围来确定空气的流态及努塞尔数的表达式，具体见表1。从而得到空气表面的自然对流表面散热系数为

(6)

式中:Nu为努塞尔数；l为特征长度(m)；λ为流体的热传导系数(W/m·℃)；h为表面散热系数(W/(m2·℃))。

2.3.2强迫对流表面散热系数的确定

在横向磁场圆筒型PMLM中动子作往返运动，其表面空气的流动对应实验关联式属于横掠圆管的强迫对流。在强制对流中，判别流态的特征数是雷诺数Re准则，因此首先计算动子表面空气流动的雷诺数为

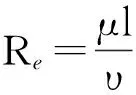
(7)

式中:μ为空气流速(m/s)；l为动子长度(m)；υ为空气的动力粘度(m2/s)。

文献[14]中给出了用表面传热系数计算准则和相关修正系数来计算其对流换热系数，其表面散热系数与表面空气的雷诺数、普朗特数相关。本文选空气的平均温度为60℃，对于不同散热面其特征长度不同、速度不同，导致雷诺数也不同，因此努赛尔数公式系数选取也不同，详见表2。强迫对流表面散热系数可计算为

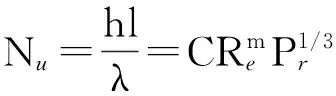
(8)

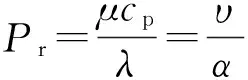
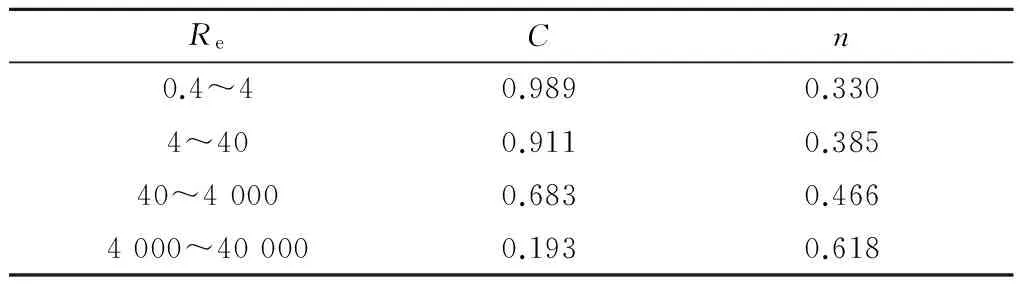
表2　努赛尔公式系数一览表[14]

由于在不同速度下空气流动的雷诺数不同，使得动子表面的散热系数随速度变化而变化。图4所示分别为轴表面S12、动子上表面S13、动子下表面S16的散热系数在不同速度下的变化情况。

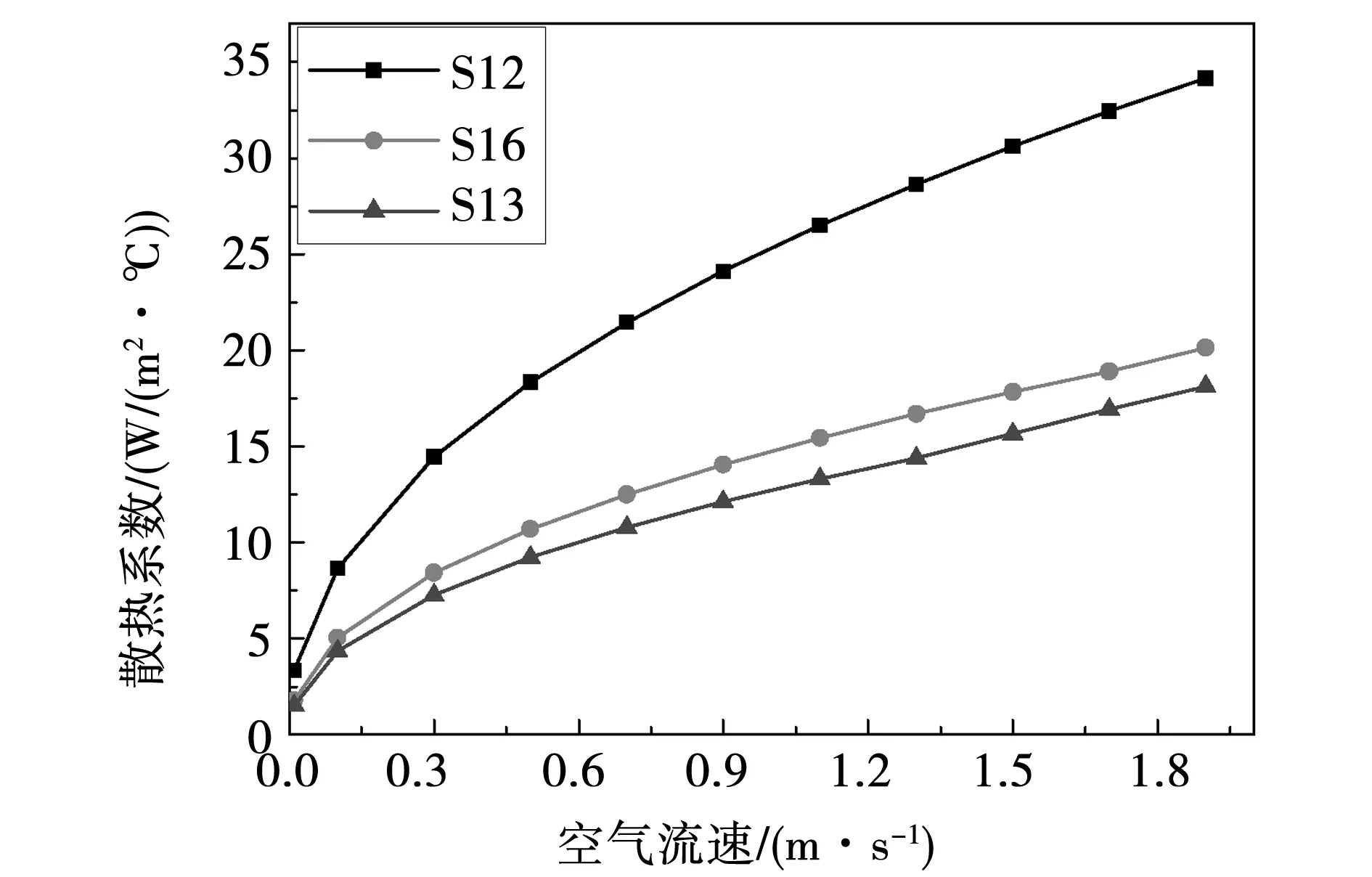
图4　散热系数随空气流速的变化曲线Fig.4　　　　Coefficient of heat transfer on the surface VS.　　　 the velocity of air

2.3.3气隙间表面散热系数的确定

定子和动子之间的热交换比较复杂，关于定子和动子间气隙表面散热系数的选取方法，可以将其归纳为两种。第一种是采用等效导热系数来计算，即把气隙等效为热传导的实体[12]；第二种是考虑气隙内流体速度及空间大小，判断其强制对流和自然对流的影响程度，根据混合对流的实验关联式[14]，分别计算气隙间动子外表面和定子内表面的散热系数。本文采用第二种方法在强制对流中考虑自然对流的影响程度，引入混合对流的判据如下：

通过判据分析可知在空气流速0.3 m/s到2 m/s之间，气隙间散热系数需通过混合对流的努赛尔数公式计算得到，有

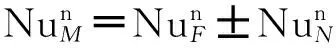
(9)

式中：NuM为混合对流时的努赛尔数；NuF为强制对流关联式计算得到的努赛尔数；NuN为自然对流关联式计算得到的努赛尔数；n为常数，一般取3。

图5所示为气隙间定子齿冠内表面S11和动子外表面S17随速度变化的对流散热系数曲线。

3横向磁场PMLM连续往复运行时温度场计算与分析

根据横向磁场圆筒型PMLM在直线伺服系统中的具体应用，对连续往复运行电机的热特性进行分析。图6为横向磁场圆筒型PMLM在连续往复运行时所加负载力59 N，速度平均值为1.0 m/s运行工况下的温度场分布图。

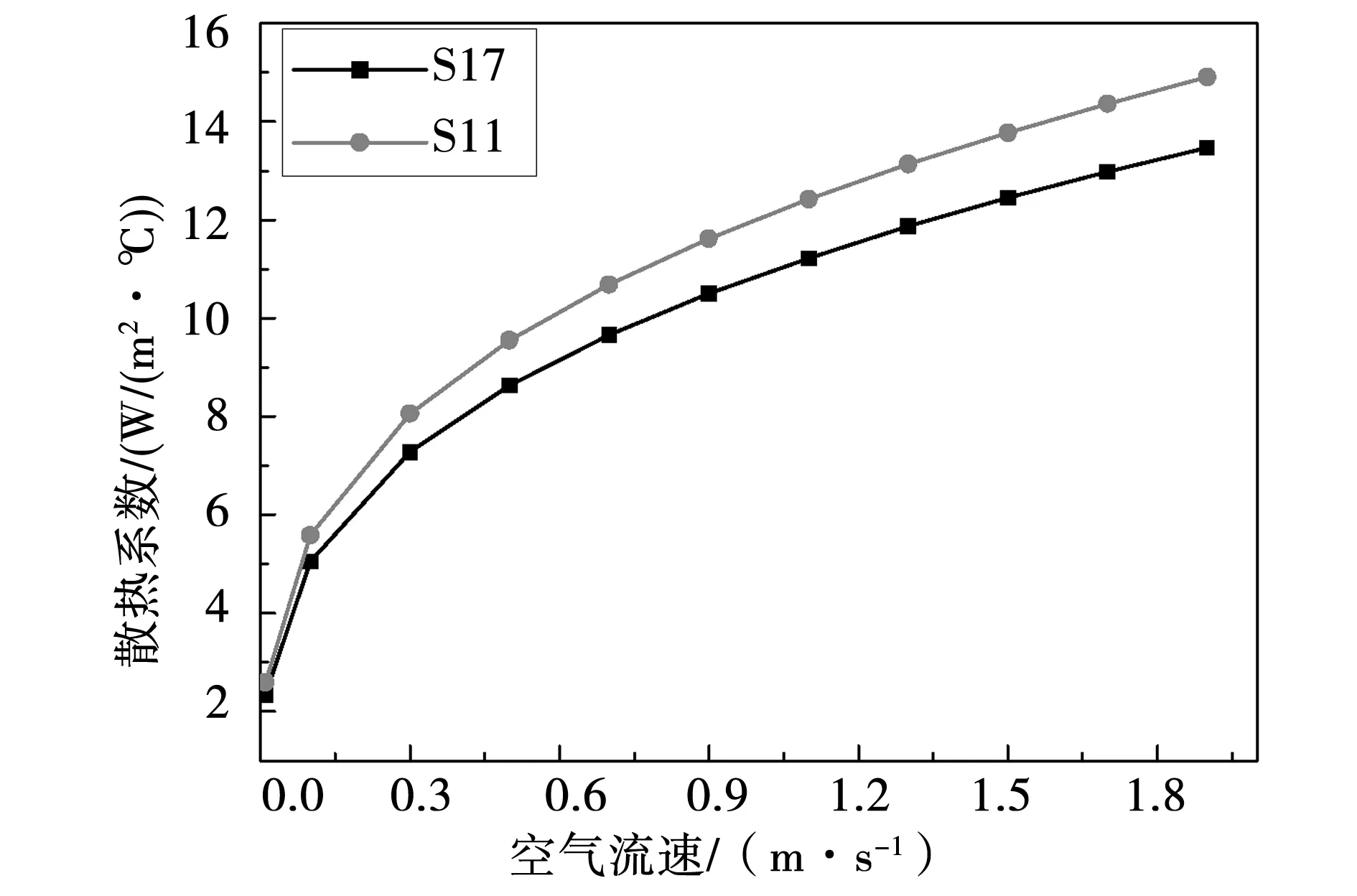
图5　散热系数随空气流速的变化曲线Fig.5　　　　Coefficient of heat transfer on the surface VS. 　　　the velocity of air

图6　　　　横向磁场圆筒型PMLM在速度平均值为1 m/s　　　下的温度场计算结果Fig.6　　　　Diagram of temperature field of transverse flux 　　　tubular PMLM with average speed of 1 m/s

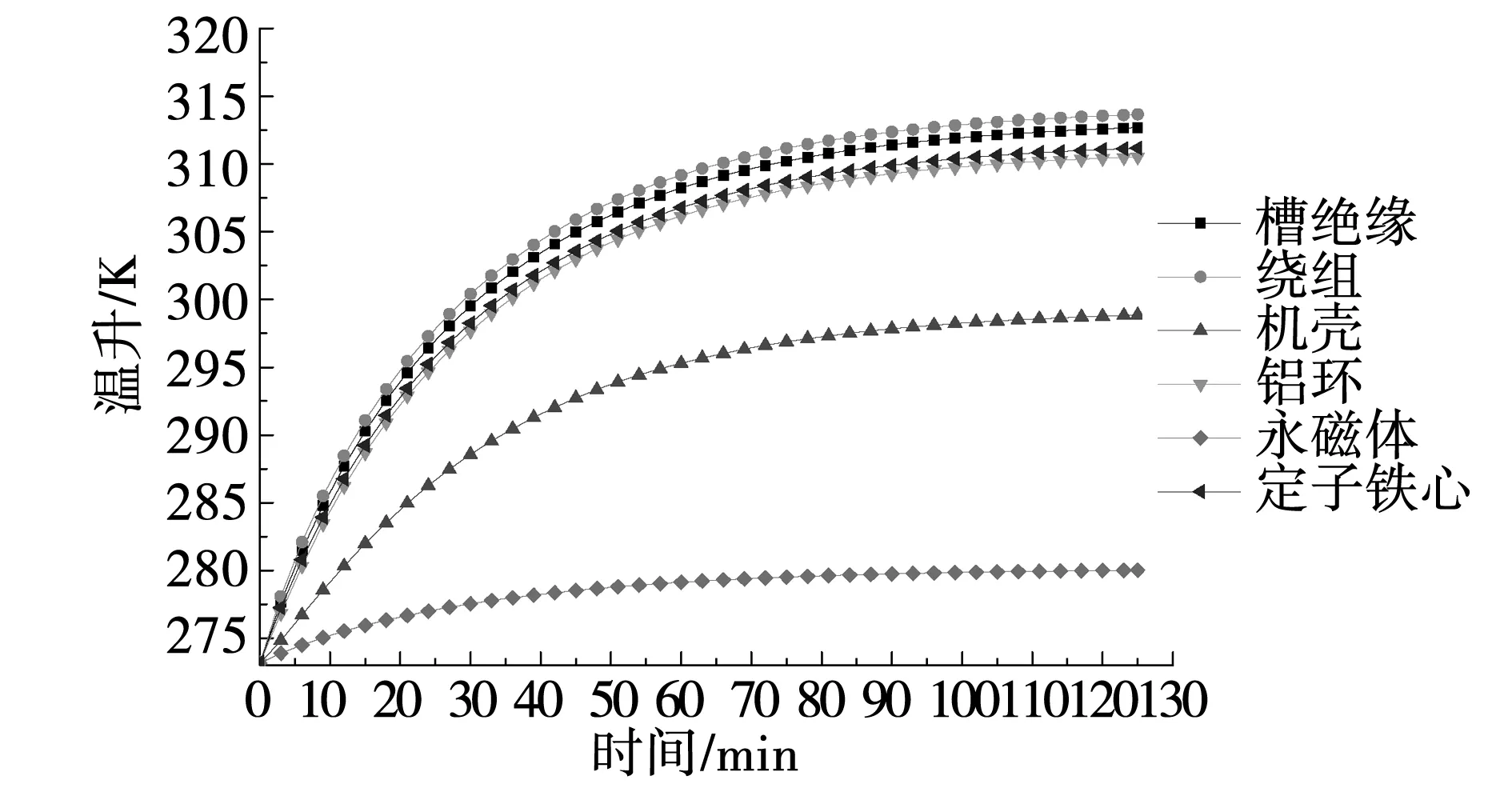
图7　横向磁场圆筒型PMLM各部件温升曲线Fig.7　　　　Curves of transverse flux tubular PMLM 　　　temperature rise

图7所示为横向磁场圆筒型PMLM在连续往复运行时所加负载力为59 N速度平均值为1 m/s下各部件的温升曲线(环境温度为24℃，对应热力学温度为273.15 K)。温升计算结果表明，横向磁场圆筒型PMLM往复运行100分钟以后，电机温升较为缓慢，基本达到热稳定状态。由于电机采用自然冷却，定子各部件(槽绝缘、定子铁心、绕组、铝环)温度差异较小，而动子上永磁体温升最低。

4连续往复运行时横向磁场PMLM温升测试

在横向磁场圆筒型PMLM温度场计算中，为了简化计算模型，做了部分等效处理。同时，电机内各等效导热系数以及各散热表面对流传热系数都是通过经验公式计算得到的，尽管这些经验公式是从试验中总结得来的，但是与实际值毕竟存在一定的误差。因此，计算结果的准确性需要通过实验加以验证。

图8为横向磁场圆筒型PMLM温升实验原理图。实验样机通过连杆机构拖动磁粉制动器来实现电机的加载。定子绕组温升采用电阻法测量，机壳表面温度采用红外测温仪来检测。

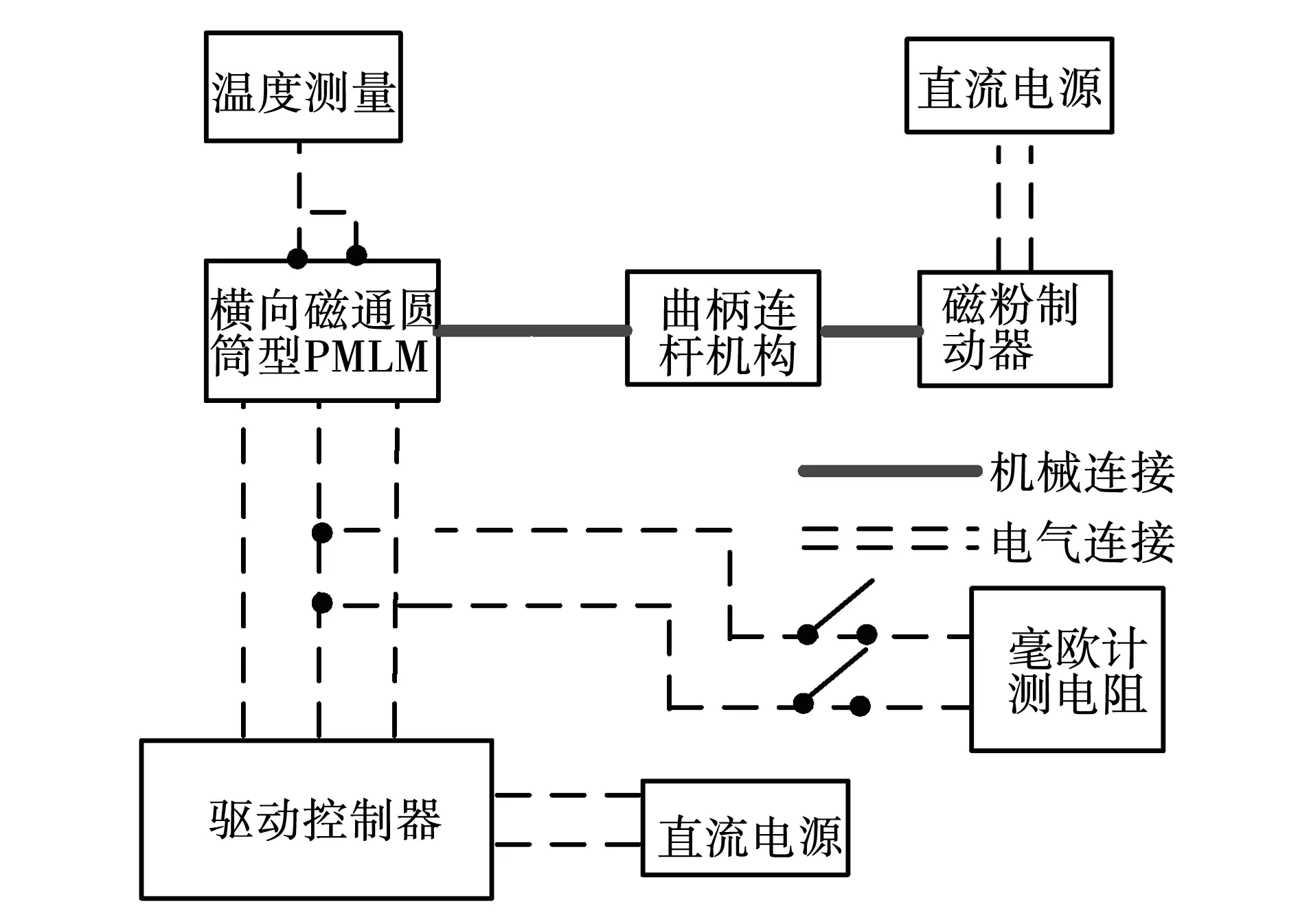
图8　温升试验原理图Fig.8　Schematic diagram of temperature rise experiment

根据温升实验原理图，设计并搭建了样机的负载实验平台如图9所示。由于直线电机行程有限，为保证其连续工作，直线电机需做往复直线运动，同时给磁粉制动器通以直流电，以保证直线电机加以合适的负载力。在实验中用磁粉制动器为横向磁场PMLM提供负载。

图10(a)和图10(b)所示分别为横向磁场圆筒型PMLM在连续往复运行下电枢绕组和机壳的实验测量值和数值计算值。由于采用电阻法测量绕组温升，通电开关的反复通断导致实测温升曲线并不光滑，而且从数值上看，计算值要小于实测值，可能的原因是损耗计算存在误差，同时导热系数和散热系数的偏差也会使得实验值与计算值存在一定的误差。

图9　温升试验加载装置Fig.9　Temperature rise experiment at load

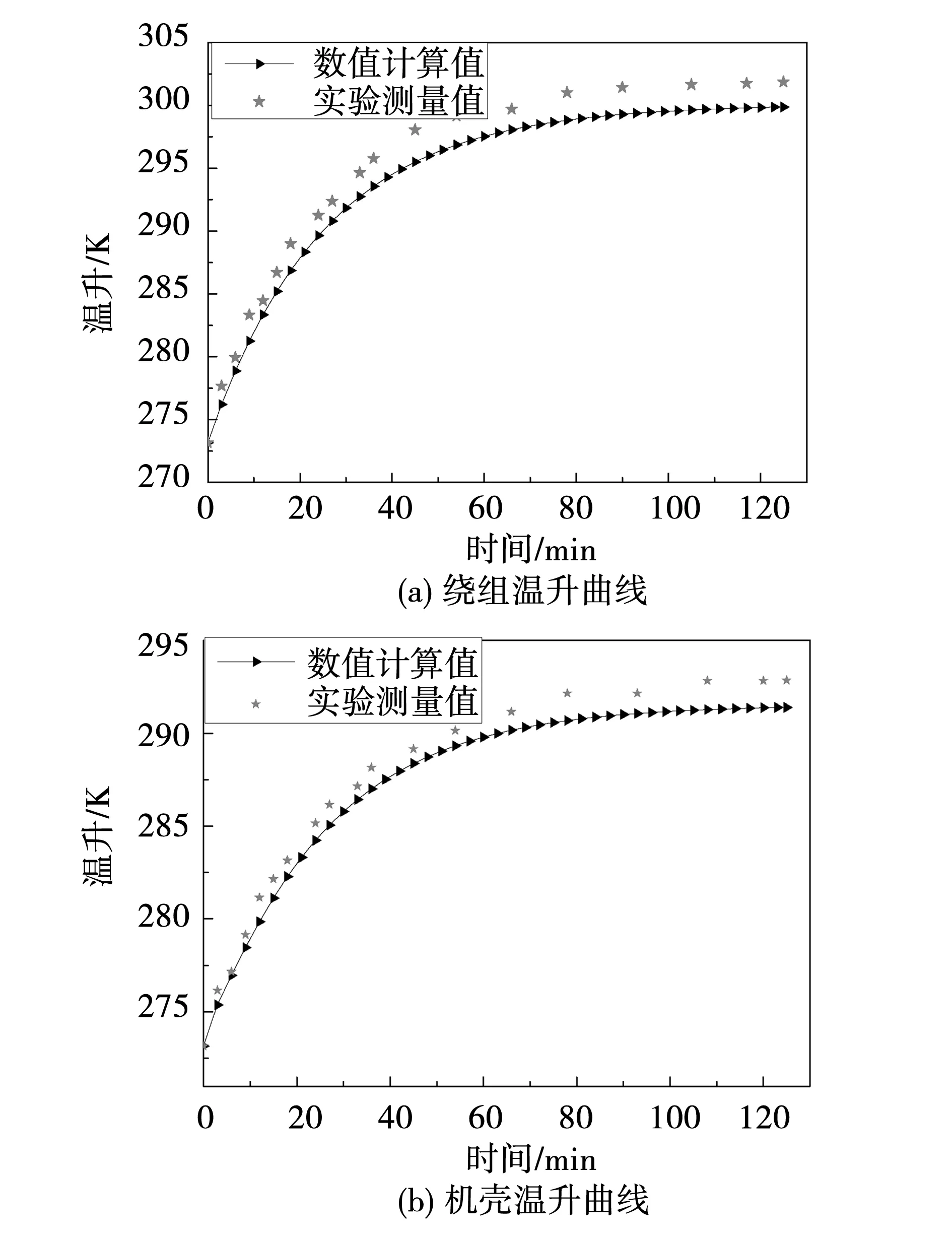
图10　温升曲线的数值计算和试验测量结果Fig.10　　　　Comparison of the prototype temperature　　　 rise curves

5结论

本文针对横向磁场圆筒型PMLM在直线伺服系统中的具体应用，对连续往复运行工况下电机的温升特性进行研究。完成的主要工作有以下几方面：

1)在综合考虑了横向磁场圆筒型PMLM结构和运行状态的特殊性的基础上，建立了包含机壳端盖在内且计及电枢绕组三维结构的三维暂态温度场计算模型。

2)应用传热学理论，在考虑电机热源、工作状态和电机各部分的热交换等因素的前提下，给出电机中材料的导热系数、比热容的确定方法，而且详细讨论了各个表面散热系数的确定方法。对横向磁场圆筒型PMLM连续往复运行工况下的瞬态温度场进行了计算，分析了整机瞬态温升过程。

3)根据横向磁场圆筒型PMLM在直线伺服系统中的具体应用，搭建了温升测试装置，对连续往复运行工况下的温升进行测试，并通过温升实验对计算结果进行了验证，从而证明该电机温度场数值计算的准确性。

参考文献:

[1]黄旭珍. 高功率密度永磁电机的损耗及温升特性的研究[D]. 哈尔滨:哈尔滨工业大学,2008: 20-45.

[2]马俊. 圆筒型直线电机模型建立及其动态温度场研究[D]. 哈尔滨:哈尔滨理工大学,2005: 30-38.

[3]孙建宏,丁文,鱼振民. 扁平型直线异步电机温度场的计算与分析[J]. 电机与控制应用,2006,33 (1): 20-24.

SUN Jianhong,DING Wen,YU Zhenmin. Calculation and analysis of thermal field for the flat linear motor[J]. Electric Machines and Control Application,2006,33(1): 20-24.

[4]KOU Baoquan,HUANG Xuzhen,WU Hongxing,et al. Thrust and thermal characteristics of electromagnetic launcher based on permanent magnet synchronous motors[J]. IEEE Transactions on Magnetics,2009,45(1): 358-362.

[5]Changsoo Jang,Jong Young Kim,Yung Joon Kim,et al. Heat transfer analysis and simplified thermal resistance modeling of linear motor driven stages for SMT Applications [J]. IEEE Transactions on Components and Packaging Technologies,2003,26(3): 532-539.

[6]Ioana-Cornelia Vese,Fabrizio Marignetti,Mircea M Radulescu. Multiphysics approach to numerical modeling of a permanent-magnet tubular linear motor [J]. IEEE Transactions on Industrial Electronics,2010,57(1): 320-326.

[7]张洪亮. 永磁同步电机铁心损耗与暂态温度场研究[D]. 哈尔滨: 哈尔滨工业大学,2010: 76-80.

[8]赵玫,邹继斌.变速往复周期运动模式下横向磁通圆筒型永磁直线电机损耗[J]. 电工技术学报，2013,28(7): 117-123.

ZHAO Mei,ZOU Jibin. The loss investigation of transverse flux tubular PMLM in variable-speed reciprocating periodic motion mode[J]. Transactions of China Electrotechnical Society,2013,28(7): 117-123.

[9]Kyle A Brucker,Joseph Majdalani. Equivalent thermal conductivity for compact heat sink models based on the churchill and chu correlation [J]. IEEE Transactions on Components and Packaging Technologies,2003,26(1): 158-164.

[10]付兴贺,林明耀,徐妲,等. 永磁-感应子式混合励磁发电机三维暂态温度场的计算与分析[J]. 电工技术学报，2013,28(3):107-113.

FU Xinghe,LIN Mingyao,XU Da,et al. Computation and analysis of 3D-transient temperature field for a permanent magnet-induction hybrid excitation generator [J]. Transactions of China Electrotechnical Society,2013,28(3):107-113.

[11]胡敏强,黄学良. 电机运行性能数值计算方法及其应用[M]. 南京: 东南大学出版社,2003: 72-77.

[12]KWON O. Analysis and experiment on the thermal characteristics of electric motors[D]. University of California,Berkeley,2001: 33-35.

[13]江善林.高速永磁同步电机的损耗分析与温度场计算[D]. 哈尔滨: 哈尔滨工业大学,2010: 120-121.

[14]杨世铭,陶文铨. 传热学[M]. 北京: 高等教育出版社,2006:197-263.

(编辑：刘琳琳)

Computation and analysis of temperature field for transverse flux permanent magnet linear motor in continuous reciprocating running

ZHAO Mei1,2,3,ZOU Ji-bin2,ZHANG Yun-liang3,HAN Fu-jun1,YANG Hong-yong1

(1.Department of Information and Electrical Engineering,Ludong University,Yantai 264025,China; 2.Department of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150001,China; 3.Weihai Guangtai Airport Equipment CO.,Limited,Post-Doctoral Research Center,Weihai 264200,China)

Abstract:According to the specific application of the transverse flux permanent magnet linear motor(PMLM) in the linear servo system,the motor thermal characteristics was studied in the condition of running back and forth for a long time. On the basis of comprehensive consideration of the particularity of motor structure and operation of state,the three-dimensional temperature field calculation model of transverse flux PMLM was established,taking into account the motor heat,work status,and motor part of the heat exchange and other factors,the motor thermal conductivity of the material,the heat capacity and heat transfer coefficient of each surface were discussed in detail.Furthermore,the changing law as heat transfer coefficient of mover surface and air-gap surfaces as speed was illustrated. The transient temperature field of the transverse flux PMLM was calculated in the condition of running back and forth for a long time.Accuracy of the numerical results was verified by the testing of the characteristics of prototype.

Keywords:transverse flux; permanent magnet linear motor; temperature field; continuous reciprocating

收稿日期:2014-09-01

基金项目：国家自然科学基金(51407088，61273152)

作者简介：赵玫(1983—)，女，博士，副教授，研究方向为直线电机及其驱动控制；

通讯作者:赵玫

DOI:10.15938/j.emc.2016.05.011

中图分类号:TM 359.4

文献标志码:A

文章编号:1007-449X(2016)05-0077-07

邹继斌(1957—)，男，教授，博士生导师，研究方向为永磁电机一体化设计；

张云亮(1980—)，男，硕士，工程师，研究方向为永磁电机及其驱动控制；

韩辅君(1975—)，男，博士，副教授，研究方向为永磁电机及其驱动控制；