借力“函数思想”巧解题
2016-06-12江苏屠莉雯
高中数理化 2016年10期
◇ 江苏 屠莉雯
借力“函数思想”巧解题
◇江苏屠莉雯
函数思想是从题目的条件出发,通过联想、构造函数模型,利用函数的性质(定义域、值域、单调性、奇偶性、周期性等)和图象,使问题获解.
1活用“函数思想”,巧解数列问题


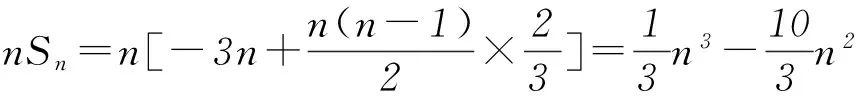



2活用“函数思想”,巧解不等式问题



作差得

①
构造函数g(a)=ea(b-a+2)+eb(b-a-2),则g′(a)=ea(b-a+1)-eb.
因为g″(a)=ea(b-a)>0,所以函数g′(a)在R上单调递增.于是,由a 从而,由a ea(b-a+2)+eb(b-a-2)>0. 3活用“函数思想”,巧解立体几何问题 图1 图2 综上,在解题中多关注“函数思想”的灵活运用,往往有助于帮助我们巧妙分析、解决相关问题,从而不断积累解题经验,逐步提升解题技能 (作者单位:江苏无锡市第一中学)






