Musical Isomorphisms and Problems of Lifts∗

Rabia CAKANKursat AKBULUTArif SALIMOV

1 Introduction

Let(M,g)be a smooth pseudo-Riemannian manifold of dimension n.We denote byM the tangent and cotangent bundles over M with local coordinatesrespectively,whereand px=pidxi∈M,∀x∈M.

A very important feature of any pseudo-Riemannian metric g is that it provides musical isomorphisms g?:TM → T∗M and g?:T∗M → TM between the tangent and cotangent bundles.Some properties of geometric structures on cotangent bundles with respect to the musical isomorphisms are proved in[1–5].

The musical isomorphisms g?and g?are expressed by

and

with respect to the local coordinates,respectively.The Jacobian matrices of g?and g?are given by

and

respectively,where δ is the Kronecker delta.

We denote by(M)the set of all diff erentiable tensor fields of type(p,q)on M.LetCXT∈(TM),CϕT∈TM)andCST∈(TM)be complete lifts of tensor fields X∈(M),ϕ∈M)and S∈(M)to the tangent bundle TM.

The aim of this paper is to study the lift properties of cotangent bundles of Riemannian manifolds.The results are significant for a better understanding of the geometry of the cotangent bundle of a Riemannian manifold.In this paper,we transfer via the differentialthe complete liftsandfrom the tangent bundle TM to the cotangent bundle T∗M.The transferred liftsare compared with the complete liftsin the cotangent bundle and we show that(a)if and only if the vector field X is a Killing vector field,if and only if the triple(M,g,ϕ),ϕ2=−IdMis an anti-Khler manifold,if and only if the metric g satisfies the Yano-Ako equations.Also we give a new interpretation of the Riemannian extension∇g should be considered as the pullback:∇g=(g?)∗Cg,whereCg is the complete lift of g to the tangent bundle TM.

2 Transfer of Complete Lifts of Vector Fields

Let X=Xi∂ibe the local expression in U ⊂ M of a vector field X ∈(M).Then the complete liftCXTof X to the tangent bundle TM is given by

with respect to the natural frame{∂i,∂i}.

Using(1.1)and(2.1),we have

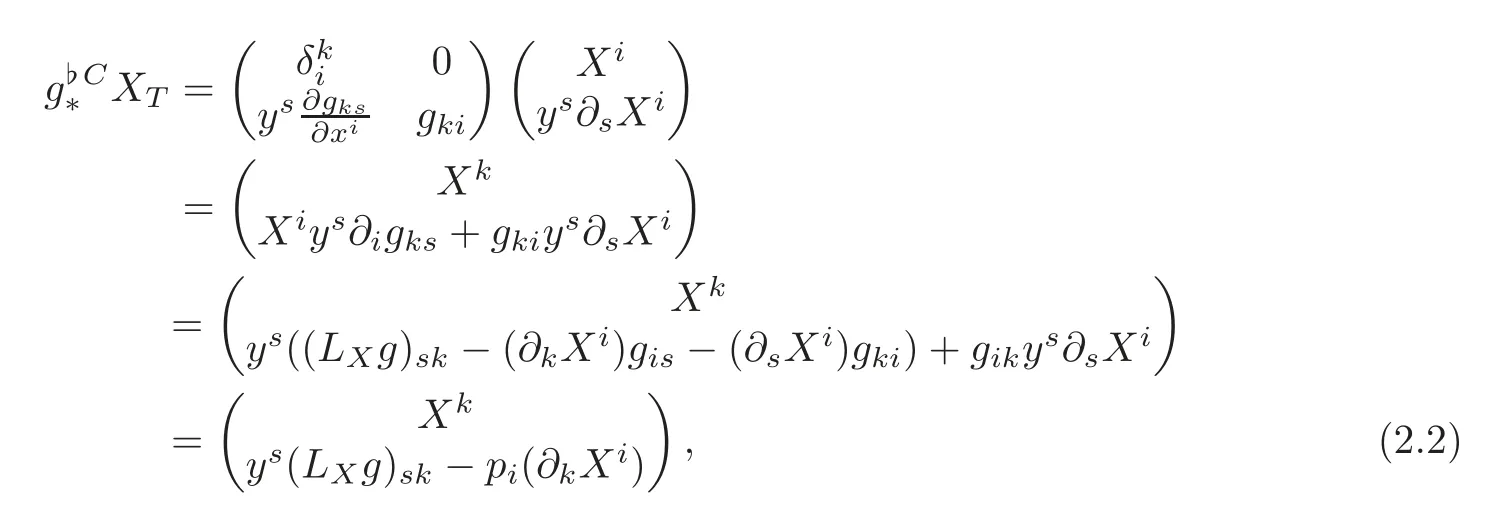
where LXis the Lie derivation of g with respect to the vector field X:

In a manifold(M,g),a vector field X is called a Killing vector field if LXg=0.It is well known that the complete liftCXT∗ of X to the cotangent bundle T∗M is given by

From(2.2)wefind

where γ(LXg)is defined by

Thus we have the following theorem.

Theorem 2.1 Let(M,g)be a pseudo-Riemannian manifold,and letCXTandCXT∗be complete lifts of a vector field X to the tangent and cotangent bundles,respectively.Then the differential(pushforward)ofCXTby g?coincides withCXT∗,i.e.,

if and only if X is a Killing vector field.

Let X and Y be Killing vector fields on M.Then we have

i.e.,[X,Y]is a Killing vector field.SinceC[X,Y]T=[CXT,CYT]andC[X,Y]T∗ =[CXT∗,CYT∗],from Theorem 2.1 we have the following result.

Corollary 2.1 If X and Y are Killing vector fields on M,then

whereis a differential(pushforward)of the musical isomorphism g?.

3 Transfer of Complete Lifts of Almost Complex Structures

Let(M,ϕ)be a 2n-dimensional,almost complex manifold,where ϕ (ϕ2= −I)denotes its almost complex structure.A semi-Riemannian metric g of the neutral signature(n,n)is an anti-Hermitian(also known as a Norden)metric if

for any X,Y ∈(M).An almost complex manifold(M,ϕ)with an anti-Hermitian metric is referred to as an almost anti-Hermitian manifold.Structures of this kind have also been studied under the name:Almost complex structures with pure(or B-)metric.An anti-K¨ahler(K¨ahler-Norden)manifold can be defined as a triple(M,g,ϕ)which consists of a smooth manifold M endowed with an almost complex structure ϕ and an anti-Hermitian metric g such that∇ϕ=0,where∇ is the Levi-Civita connection of g.It is well known that the condition∇ϕ=0 is equivalent to C-holomorphicity(analyticity)of the anti-Hermitian metric g(see[6]),i.e.,

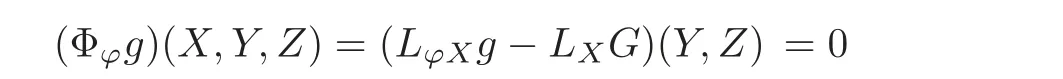
for any X,Y,Z ∈(M),where Φϕg ∈(M)and G(Y,Z)=(g◦ ϕ)(Y,Z)=g(ϕY,Z)is the twin anti-Hermitian metric.It is a remarkable fact that(M,g,ϕ)is anti-K¨ahler if and only if the twin anti-Hermitian structure(M,G,ϕ)is anti-K¨ahler.This is of special significance for anti-K¨ahler metrics since in such case g and G share the same Levi-Civita connection.

Let ϕ =∂i⊗ dxjbe the local expression in U ⊂ M of an almost complex strucure ϕ.Then the complete liftCϕTof ϕ to the tangent bundle TM is given by(see[8,p.21])

with respect to the induced coordinates(xi,xi)=(xi,yi)in TM.It is well known thatCϕTdefines an almost complex structure on TM,if and only if so does ϕ on M.

Using(1.1)–(1.2)and(3.1),we have

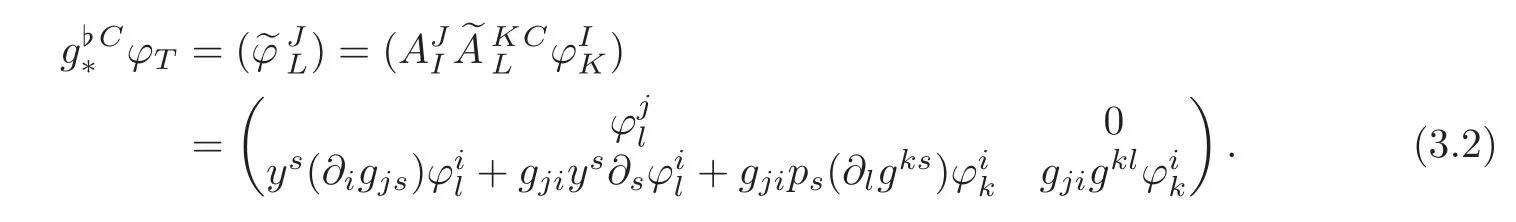
Since g=(gij)and g−1=(gij)are pure tensor fields with respect to ϕ,wefind

and

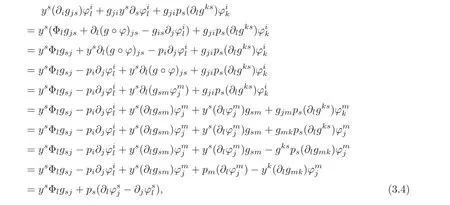
where

Substituting(3.3)–(3.4)into(3.2),we obtain

It is well known that the complete liftCϕT∗ of ϕ ∈ ?10(M)to the cotangent bundle is given by(see[8,p.242])

with respect to the induced coordinates in T∗M.Thus we obtain

where

From here,we have the following theorem.

Theorem 3.1 Let(M,g,ϕ)be an almost anti-Hermitian manifold,and letCϕTandCϕT∗be complete lifts of an almost complex structure ϕ to the tangent and cotangent bundles,respectively.Then the differential ofCϕTby g?coincides withCϕT∗,i.e.,g?∗CϕT=CϕT∗if and only if(M,g,ϕ)is an anti-K¨ahler(Φϕg=0)manifold.

4 Transfer of Complete Lifts of the Vector-Valued 2-Form

Let S be a vector-valued 2-form on M.A semi-Riemannian metric g is called pure with respect to S if

for any X1,X2,Y∈M),where SYdenotes a tensor field of type(1,1)such that

for any Y,Z∈(M).The condition of purity of g may be expressed in terms of the local components as follows:

We now define the Yano-Ako operator

where(g◦S)(X,Y1,Y2)=g(S(X,Y1),Y2).The Yano-Ako operator has the following components with respect to the natural coordinate system:

The non-zero components of the complete liftCSTof S to the tangent bundle TM are given by(see[8,p.22])

Using(1.1)and(1.2),we can easily verify that

and I,J,···=1,···,2n has non-zero components of the form

i.e.,the transfer g?∗CSTcoincides with the complete liftCST∗of the vector-valued 2-form S∈∧2(M)to the cotangent bundle if and only if

Thus we have the following theorem.

Theorem 4.1 Let g be a pure pseudo-Riemanian metric with respect to the vector-valued 2-form S ∈ ∧2(M),and letCSTandCST∗be complete lifts of S to the tangent and cotangent bundles,respectively.Then

if and only if g satisfies the following Yano-Ako equation:

①论证范围内地下水资源评价，根据论证范围内的地下水补、径、排条件，计算各项补给量和排泄量，并进行均衡分析，分析补给量计算的可靠性。

where ΦSg is the operator defined by(4.1).

5 Transfer of Complete Lifts of Metrics

LetCg be a complete lift of a pseudo-Riemannian metric g to TM with components

Using(1.2)and(5.1)we see that the pullback ofCg by g?is the(0,2)-tensor field(g?)∗Cg on T∗M and has components

On the other hand,a new pseudo-Riemannian metric∇g∈(T∗M)on T∗M is defined by the equation(see[8,p.268])

for any X,Y ∈(M),where γ(∇XY+ ∇YX)is a function in π−1(U) ⊂ T∗M with a local expression

and is called a Riemannian extension of the Levi-Civita connection∇g to T∗M.The Riemannian extension∇g has components of the form

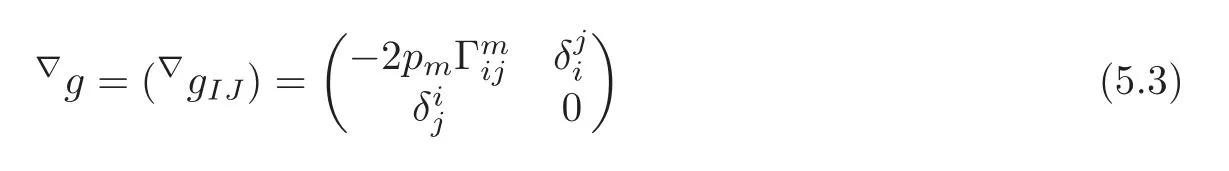
with respect to the natural frame{∂i,∂ı}.Thus,from(5.2)and(5.3)we obtain(g?)∗Cg=∇g,i.e.,we have the following theorem.

Theorem 5.1 The Riemannian extension∇g∈(T∗M)is a pullback of the complete liftCg∈TM).

[1]Bejan,C.,Almost para-Hermitian structures on the tangent bundle of an almost para-co-Hermitian manifold,Proceedings of the Fifth National Seminar of Finsler and Lagrange Spaces(Bra¸sov,1988),Soc.S¸tiinte Mat.R.S.,Romania,Bucharest,1989,105–109.

[2]Cruceanu,V.,Une classe de structures g´eom´etriques sur lefibr´e cotangent,International Conference on Differential Geometry and Its Applications(Bucharest,1992),Tensor(N.S.),Vol.53,Commemoration Volume I,1993,196–201.

[3]Cruceanu,V.,Fortuny,P.and Gadea,P.M.,A survey on paracomplex geometry,Rocky Mountain J.Math.,26(1),1996,83–115.

[4]Druta,S.L.,Classes of general natural almost anti-Hermitian structures on the cotangent bundles,Mediterr.J.Math.,8(2),2011,161–179.

[5]Druta-Romaniuc,S.L.,Riemannian almost product and para-Hermitian cotangent bundles of general natural lift type,Acta Math.Hungar.,139(3),2013,228–244.

[6]Salimov,A.A.,On operators associated with tensor fields,J.Geom.,99(1–2),2010,107–145.

[7]Yano,K.and Ako,M.,On certain operators associated with tensor fields,Kodai Math.Sem.Rep.,20,1968,414–436.

[8]Yano,K.and Ishihara,S.,Tangent and cotangent bundles,Pure and Applied Mathematics,Marcel Dekker,Inc.,New York,1973.