Brake Subharmonic Solutions of Subquadratic Hamiltonian Systems∗

Chong LI

1 Introduction and the Main Results

Consider the Hamiltonian systems

whereis the standard symplectic matrix,Inis the unit matrix of order n,H∈C2(R×R2n,R)and∇H(t,z)is the gradient of H(t,z)with respect to the space variable z.We denote the standard norm and inner product in R2nby|·|and(·,·),respectively.

Suppose that H(t,z)=and H∈C2(R×R2n,R)satisfies the following conditions:

(H4)There exist constants a1,a2>0 and α∈(0,1)such that

(H6)is a symmetrical continuous matrix,semi-positively definite for all t∈R;

Recall that a T-periodic solution(z,T)of(1.1)is called a brake solution if z(t+T)=z(t)and z(t)=Nz(−t),and the later is equivalent toin which T is called the brake period of z.Up to the author’s knowledge,H.Seifert firstly studied brake orbits in the second-order autonomous Hamiltonian systems in[27]of 1948.Since then,many studies have been carried out for brake orbits of the first-order and second-order Hamiltonian systems.For the minimal periodic problem,multiple existence results about brake orbits for the Hamiltonian systems and more details about brake orbits,one can refer to the papers(see[1,3–6,11–13,20,22,25,29])and the references therein.S.Bolotin proved first in[5](also see[6])of 1978 the existence of brake orbits in the general setting.K.Hayashi in[13],H.Gluck and W.Ziller in[11],and V.Benci in[3]in 1983–1984 proved the existence of brake orbits of second-order Hamiltonian systems under certain conditions.In 1987,P.Rabinowitz in[25]proved the existence of brake orbits of the first-order Hamiltonian systems.In 1989,V.Benci and F.Giannoni gave a different proof of the existence of one brake orbit in[4].In 1989,A.Szulkin in[29]proved the existence of brake orbits of the first-order Hamiltonian systems under the√2-pinched condition.E.van Groesen in[12]of 1988 and A.Ambrosetti,V.Benci,Y.Long in[1]of 1993 also proved the multiplicity result about brake orbits for the second order Hamiltonian systems under different pinching conditions.Without pinching conditions,in[22]Y.Long,D.Zhang and C.Zhu proved that there exist at least two geometrically distinct brake orbits in every bounded convex symmetric domain in Rnfor n≥2.Recently,C.Liu and D.Zhang in[20]proved that there exist at least+1 geometrically distinct brake orbits in every bounded convex symmetric domain in Rnfor n≥2,and there exist at least n geometrically distinct brake orbits on the nondegenerate domain.D.Zhang studied the minimal period problem for brake orbits of nonlinear autonomous reversible Hamiltonian systems in[30].

For the non-autonomous Hamiltonian systems,and the periodic boundary(brake solution)problems,since the Hamiltonian function H is T-periodic in the time variable t,if the system(1.1)has a T-periodic solution(z1,T),one hopes to find the jT-periodic solution(zj,jT)for integer j≥1,for example,(z1,jT)itself is a jT-periodic solution.The subharmonic solution problem asks when the solutions z1and zjare geometrically distinct.More precisely,in the case of brake solutions,z1and zjare distinct iffor any integer k.Below we remind that the L0-indices of the two solutions z1and(kT)∗z1for any k∈Z in the interval?0,?are the same.

Theorem 1.1 Suppose that H ∈ C2(R×R2n,R)satisfies(H1)–(H7),and then for each integerthere is a jT-periodic nonconstant brake solution zjof(1.1)such that zjand zkjare distinct for k ≥ 5 andFurthermore,{zkp|p∈ N}is a pairwise distinct brake solution sequence of(1.1)for k≥5 and 1≤

Especially,ifTherefore,one can state the following theorem.

Theorem 1.2 Suppose that H ∈ C2(R×R2n,R)with(t)≡ 0 satisfies(H1)–(H5),and then for each integer j≥1,there is a jT-periodic nonconstant brake solution zjof(1.1).Furthermore,given any integers j≥1 and k≥5,zjand zkjare distinct brake solutions of(1.1),and in particularly,{zkp|p∈N}is a pairwise distinct brake solution sequence of(1.1).

The first result on subharmonic periodic solutions for the Hamiltonian systems˙z(t)=J∇H(t,z(t)),where z∈ R2nand H(t,z)is T-periodic in t,was obtained by P.Rabinowitz in his pioneer work[26].Since then,many new contributions have appeared(see,for example,[8–9,19,21,28]and the references therein).Especially,in[9],I.Ekeland and H.Hofer proved that under a strict convex condition and a superquadratic condition,the Hamiltonian system ˙z(t)=J∇H(t,z(t))possesses a subharmonic solution zkfor each integer k≥1 and all of these solutions are pairwise geometrically distinct.In[19],C.Liu obtained a result of subharmonic solutions for the non-convex case by using the Maslov-type index iteration theory.In[14],the author of this paper and C.Liu obtained a result of brake subharmonic solutions for the superquadratic condition by using the L-Maslov type index iteration theory.For the subquadratic Hamiltonian systems,P.Rabinowitz[26]proved the existence of subharmonic solutions for the Hamiltonian system(1.1)under conditions(H4)–(H5)for the special case α =0.In[28],E.A.B.Silva obtained the existence of subharmonic solutions for the Hamiltonian system(1.1)under conditions(H4)–(H5),by establishing a new version of a saddle point theorem for strongly in definite functionals which satisfy a generalization of the well-known(PS)condition.In this paper,we mainly use the L-Maslov type index iteration theory to study the brake subharmonic solutions under the subquadratic conditions.

The main ingredient in proving Theorems 1.1–1.2 is to transform the brake solution problem into the L0-boundary problem:

where L0={0}⊕Rn∈ Λ(n).Λ(n)is the set of all linear Lagrangian subspaces in(R2n,ω0),where the standard symplectic form is defined byA Lagrangian subspace L of R2nis an n dimensional subspace satisfying ω0|L=0.Then we use the Galerkin approximation methods to get a critical point of the action functional which is also a solution of(3.1)with a suitable L0-index estimate(see Theorem 3.1 below).

The L-Maslov type index theory for any L∈Λ(n)was studied in[17]by the algebraic methods.In[22],Y.Long,D.Zhang and C.Zhu established two indices μ1(γ)and μ2(γ)for the fundamental solution γ of a linear Hamiltonian system by the methods of functional analysis which are special cases of the L-Maslov type index iL(γ)for Lagrangian subspaces L0={0}⊕Rnand L1=Rn⊕{0}up to a constant n.In order to prove Theorem 1.1,we need to consider the problem(3.1).The iteration theory of the L0-Maslov type index theory was developed in[18]and[20],which helps us to distinguish solutions zjfrom zkjin Theorems 1.1–1.2.

This paper is divided into 3 sections.In Section 2,we give an introduction to the Maslovtype index theory for symplectic paths with Lagrangian boundary conditions and an iteration theory for the L0-Maslov type index theory.In Section 3,we give the proofs of Theorems 1.1–1.2.

2 Preliminaries

In this section,we briefly recall the Maslov-type index theory for symplectic paths with Lagrangian boundary conditions and an iteration theory for the L0-Maslov type index theory.All the details can be found in[16–18,20].

We denote the 2n-dimensional symplectic group Sp(2n)by where L(R2n)is the set of all real 2n×2n matrices,and MTis the transpose of matrix M.Denote by Ls(R2n)the subset of L(R2n)consisting of symmetric matrices.And denote the symplectic path space by

We write a symplectic path γ∈P(2n)in the following form:

where S(t),T(t),V(t)and U(t)are n×n matrices.The n vectors that come from the column of the matrixare linearly independent and they span a Lagrangian subspace of(R2n,ω0).Particularly,at t=0,this Lagrangian subspace is L0={0}⊕Rn.

definition 2.1(see[17])We define the L0-nullity of any symplectic path γ∈P(2n)by

with the n×n matrix function V(t)defined in(2.1).

For L0={0}⊕Rn,We define the following subspaces of Sp(2n)by

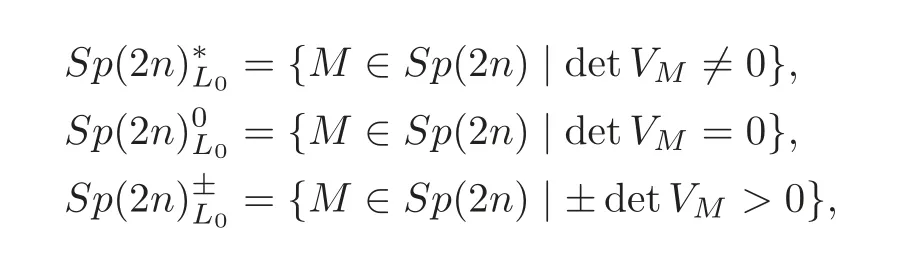
whereandWe denote two subsets of P(2n)by

We note that rankso the complex matrixis invertible.We define a complex matrix function by

It is easy to see that the matrix Q(t)is a unitary matrix for any t∈[0,1].We define

For a pathwe first adjoin it with a simple symplectic path starting from J=−M+,that is,we define a symplectic path by

Then we choose a symplectic path β(t)in Sp(2n)starting from γ(1)and ending at M+or M−according to γ(1)respectively.We now define a joint path by

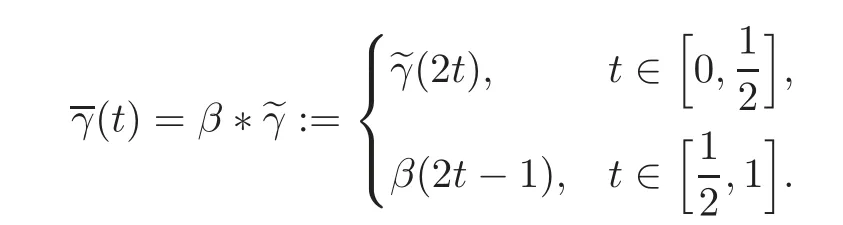
By the definition,we see that the symplectic path γ starts from −M+and ends at either M+or M−.As above,we define

forWe can choose a continuous function Δ(t)in[0,1]such that

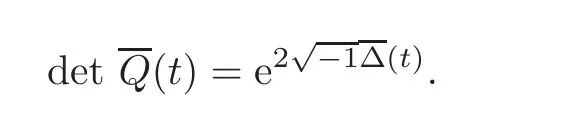
By the above arguments,we see that the number∈Z and it does not depend on the choice of the function

definition 2.2(see[17])For a symplectic pathwe define the L0-index of γ

definition 2.3(see[17])For a symplectic pathwe define the L0-index of γandis sufficiently close to γ}.

We know thatwhich means that for any linear subspace L∈Λ(n),there is an orthogonal symplectic matrix P=the unitary matrix,such that PL0=L.P is uniquely determined by L up to an orthogonal matrix C∈O(n).It means that for any other choice P?satisfying the above conditions,there exists a matrix C∈O(n)such thatWe define the conjugated symplectic path γc∈ P(2n)of γ by γc(t)=P−1γ(t)P.

definition 2.4(see[17])We define the L-nullity of any symplectic path γ∈P(2n)by

where the n × n matrix function Vc(t)is defined in(2.1)with the symplectic path γ replaced by

definition 2.5(see[17])For a symplectic path γ ∈ P(2n),we define the L-index of γ by iL(γ)=iL0(γc).

In the case of linear Hamiltonian systems,

where B ∈ C(R,Ls(R2n)).Its fundamental solution γ = γBis a symplectic path starting from the identity matrix I2n,i.e.,γ=γB∈P(2n).We denote

Theorem 2.1 (see[17])Suppose that γ ∈P(2n)is a fundamental solution of(2.2)with B(t)>0.There holds iL(γ)≥ 0.

Suppose that the continuous symplectic path γ :[0,2]→ Sp(2n)is the fundamental solution of(2.2)with B(t)satisfying B(t+2)=B(t)and B(1+t)N=NB(1−t).This implies that B(t)N=NB(−t).By the unique existence theorem of the differential equations,we get

We define the iteration path of γ|[0,1]by

and in general,for k∈N,we define

Recall that(iω(γ),νω(γ))is the ω-index pair of the symplectic path γ introduced in[21],andis defined in[20].

Theorem 2.2(see[20])Suppose thatFor odd k we have

and for even k,we have

where

Theorem 2.3(see[20])There hold

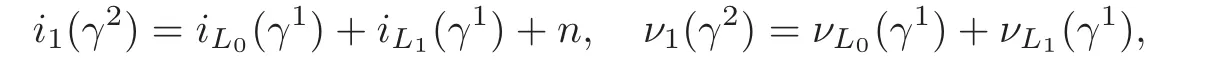
where L1=Rn⊕{0}∈Λ(n).

In the following section,we need the following two iteration inequalities.

Theorem 2.4(see[18])For any γ∈P(2n)and k∈N,there hold

Remark 2.1 From(3.21)of[20]and Proposition B of[22],we have that

3 Proof of Theorems 1.1–1.2

In reference[14],we have proved the following Lemma 3.1.

Lemma 3.1 Suppose that the Hamiltonian function H satisfies(H1)–(H2)and(H7).If?z,?is a solution of the problem(1.2),then(,T)is a T-periodic solution of the Hamiltonian system(1.1)satisfying the brake conditionwhereis defined by

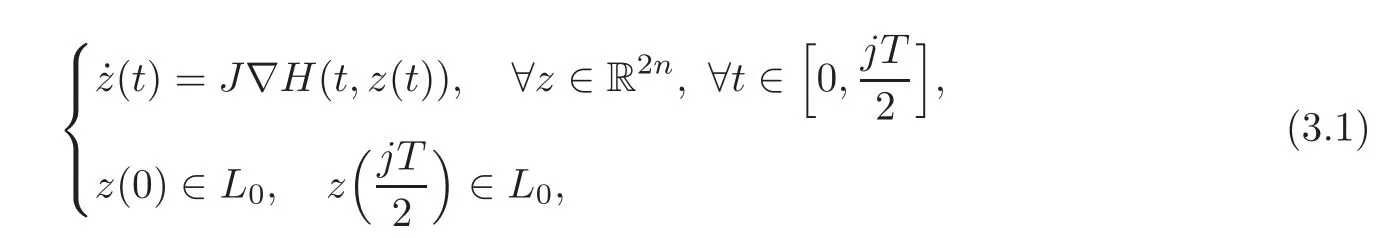
By this observation,we consider the following Hamiltonian system:where j∈N.The following result is the first part of Theorem 1.1.

Theorem 3.1 Suppose that H(t,z) ∈ C2(R × R2n,R)satisfies(H4)–(H6),and then(3.1)possesses at least one nontrivial solution zjwhose L0-index pair(iL0(zj),νL0(zj))satisfies

So we get a nonconstant brake solution(?zj,jT)with a brake period jT of the Hamiltonian system(1.1)by Lemma 3.1.

In order to prove Theorem 3.1,we need the following arguments.For simplicity,we supposebe the Hilbert space with the inner product

In the following,we use?·,·?and?·?to denote the inner product and the norm in X,respectively.It is well known that for any z∈X,one has z∈Lr([0,j],R2n)for any r∈[1,+∞),and there exists a constant cr>0 such that?z?Lr≤cr?z?.

We define the linear operators A andon X by extending the bilinear form

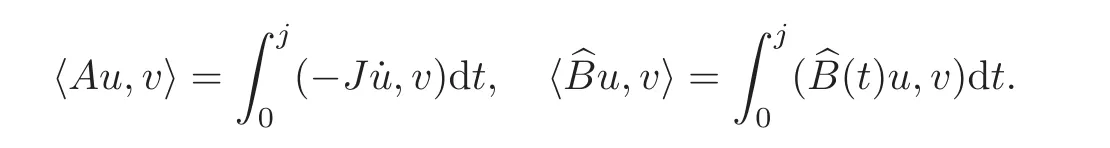
Thenis a compact self-adjoint operator(see[21])and A is a self-adjoint operator,i.e.,

We take the spaces

andWe haveWe also know that

Equalities(3.2)and(3.3)can be proved by definition and direct computation.Let Pm:X→Xmbe the corresponding orthogonal projection for m ∈N.Then Γ={Pm;m ∈N}is a Galerkin approximation scheme with respect to A(see[16]).

For any Lagrangian subspace L∈Λ(n),suppose P∈Sp(2n)∩O(2n)such that L=PL0.Then we define XL=PX and=PXm.Let Pm:XL→Then as above,={Pm;m∈N}is a Galerkin approximation scheme with respect to A.For d>0,we denote by(Q),∗=+,0,−,the eigenspaces corresponding to the eigenvalues λ of the linear operator Q:XL→ XLbelonging to[d,+∞),(−d,d)and(−∞,−d],respectively.And denote by M∗(Q),∗=+,0,−,the eigenspaces corresponding to the eigenvalues λ of Q belonging to(0,+∞),{0}and(−∞,0),respectively.For any adjoint operator Q,we denote Q?=(Q|ImQ)−1,and we also denote PmQPm=(PmQPm)|XmL.The following result is the well-known Galerkin approximation formula,which is proved in[16].

Theorem 3.2 For any B(t)∈ C([0,1],Ls(R2n))with its L-index pair(iL(B),νL(B))and any constant 00 such that for m≥m0,we have

define a function ϕ on X by

Suppose that W is a real Banach space,g∈C1(W,R).g is said to satisfy the(PS)condition,if for any sequence{xq}⊂W satisfying that g(xq)is bounded and g?(xq)→0 as q→∞,there exists a convergent subsequence{xqj}of{xq}(see[24]).Let ϕm= ϕ|Xmbe the restriction of ϕ on Xm.When H satisfies(H4)and(H5),by Proposition A in[2],we have the following two lemmas.

Lemma 3.2 For all m∈N,ϕmsatisfies the(PS)condition on Xm.

Lemma 3.3 ϕ satisfies the(PS)∗condition on X with respect to{zm},i.e.,for any sequence{zm}⊂X satisfying that zm∈ Xm,ϕm(zm)is bounded and thatas m→+∞,where(Xm)?is the dual space of Xm,there exists a convergent subsequence{zmj}of{zm}in X.

In order to proveTheorem 3.1,we need the following definition and the saddle-point theorem.

definition 3.1(see[10])Let E be a C2-Riemannian manifold and D be a closed subset of E.A family φ(α)of subsets of E is said to be a homological family of dimensional q with boundary D if for some nontrivial class,α ∈ Hq(E,D).The family φ(α)is defined by

where i∗is the homomorphism induced by the immersion i:G→E.

Theorem 3.3(see[10])For the above E,D and α,let φ(α)be a homological family of dimension q with boundary D.Suppose that f∈C2(E,R)satisfies the(PS)condition.define

Suppose thatFredholm on

Then there exists an x∈Kc(f)such that the Morse index m−(x)and the nullity m0(x)of the functional f at x satisfy

It is clear that a critical point of ϕ is a solution of(3.1).For a critical point z=z(t),let B(t)=H??(t,z(t)),and define the linearized systems at z(t)by

Then the L0-index pair of z is defined by(iL0(z),νL0(z))=(iL0(B),νL0(B)).

Now we give the proof of Theorem 3.1.

Proof of Theorem 3.1 We carry out the proof in 2 steps.

Step 1 The critical points of ϕm.

Set Sm=⊕X0.Then dim Sm=mn+dim X0=mn+dim ker A=mn+n,dim=mn.

In the following,we prove that ϕm(z)satisfies:

(I)ϕm(z)≥β>0,∀z∈ Ym=∩∂Bρ(0),

(II)ϕm(z)≤ 0< β,∀z∈ ∂Qm,where Qm={re|r∈ [0,r1]}⊕(Br2(0)∩Sm),e∈X+m∩∂B1(0),r1>ρ,r2>0.

First we prove(I).By(H4),we have?H(t,z)≤ d1|z|1+α+d2|z|+d3,where d1,d2,d3>0.Take z∈Ym,and then

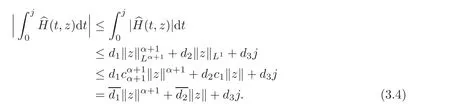
Hence by(3.2)and(3.4),

Since 1≤j<,choose a large enough ρ >0 independent of m such that for z ∈ Ym,ϕm(z)≥β>0.Hence(I)holds.

Now we prove(II).Let e∈∩∂B1and z=z−+z0∈Sm.By(3.2)and(3.3),

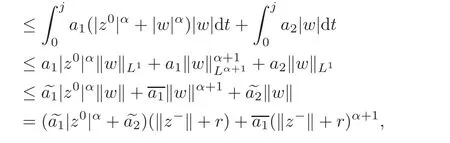
where w=z−+re and?w?=?z−?+r,Then we can obtain

It follows from(H5)thatbounded from below onhas an upper bound.Choose r1and r2independent of m such that ϕm(z+re)≤ 0< β on∂Qm.Hence(II)holds.

Because Qmis the deformation retract of Xm,then Hq(Qm,∂Qm)Hq(Xm,∂Qm),where q=dim Sm+1=mn+n+1=dim Qm,and∂Qmis the boundary of Qmin Sm⊕{Re}.But Hq(Qm,∂Qm)Hq−1(Sq−1)R.Denote by i:Qm→ Xmthe inclusion map.Let α =[Qm]∈ Hq(Qm,D)be a generator.Then i∗α is nontrivial in Hq(Xm,∂Qm),and φ(i∗α)defined by definition 3.1 is a homological family of dimension q with boundary D:=∂Qmand Qm∈ φ(i∗α).∂Qmand Ymare homologically linked(see[7]).By Lemma 3.2,ϕmsatisfies the(PS)condition.defineWe have

Since Xmis finite dimensionalis Fredholm.By Theorem 3.3,ϕmhas a critical pointwith critical value cm,and the Morse index m−()and nullity m0)of zsatisfy

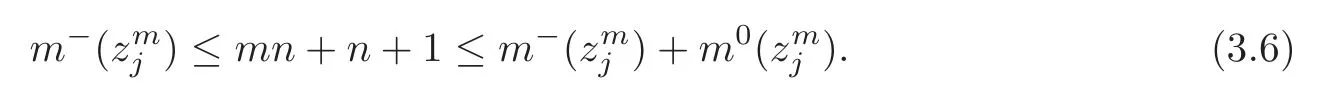
Since{cm}is bounded,passing to a subsequence,supposeBy the(PS)∗condition of Lemma 3.3,passing to a subsequence,there exists a zj∈X such that

Step 2Since

there exists an r3>0 such that

Then for m large enough,there holds

Thus by(3.8),

Similarly,we have

By Theorem 3.2 and(3.6),(3.9)–(3.10),for large m we have

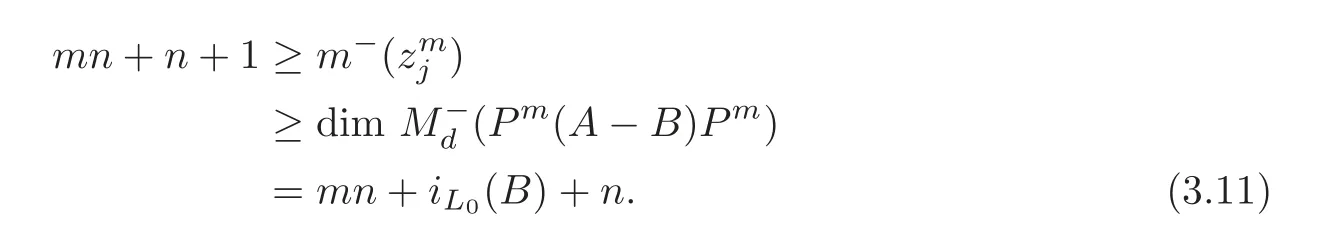
We also have

Combining(3.11)and(3.12),we have

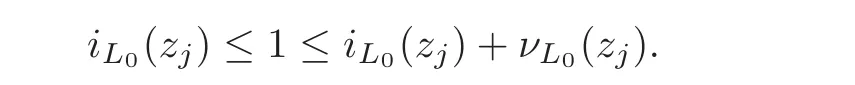
The proof of Theorem 3.1 is complete.

It is the time to give the proof of Theorem 1.1.

Proof of Theorem 1.1 For 1≤k<,by Theorem 3.1,we obtain that there is a nontrivial solution(zk,k)of the Hamiltonian systems(3.1)and its L0-index pair satisfies

Then by Lemma 3.1,(,2k)is a nonconstant brake solution of(1.1).

For k∈2N−1,we suppose that,2)and(,2k)are not distinct.By(3.13),Theorems 2.3–2.4,we have

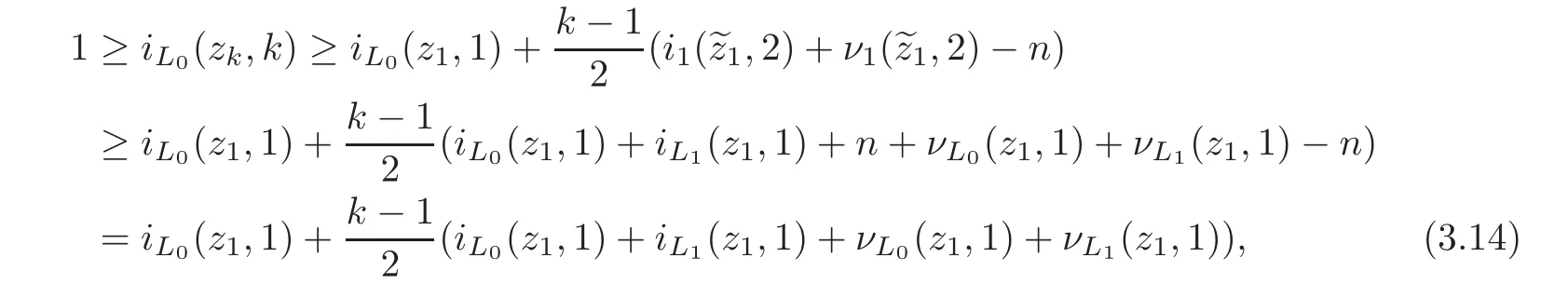
where L1=Rn⊕{0}∈Λ(n).By(H3),(H6)and Theorem 2.1,we have iL1(z1,1)≥0.We also know that νL1(z1,1)≥ 0 and iL0(z1,1)+ νL0(z1,1)≥ 1.Then(3.14)is

By 0 ≤ iL0(z1,1)≤ 1,from(3.15)we haveIt is contradictory to k≥5.Similarly,we have that for each k∈2N−1,k≥5 and kjare distinct brake solutions of(1.1).Furthermore,are pairwise distinct brake solutions of(1.1),where k ∈ 2N−1,k≥ 5 and 1

For k∈2N,as above,we suppose thatare not distinct.By(3.13),Theorems 2.3–2.4,we have

Similarly,we also know that iL1(z1,1)≥ 0,νL1(z1,1)≥ 0,iL0(z1,1)+νL0(z1,1)≥ 1.By Remark 2.1,we haveThen(3.16)is

By 0≤iL0(z1,1)≤1,from(3.17)we haveIt contradicts k≥5.Similarly we have that for each k∈2N,k≥6 andandare distinct brake solutions of(1.1).Furthermore,are pairwise distinct brake solutions of(1.1),where k∈2N,k≥6 andwith p∈ N.

In all,for any integer 1≤j

We note that Theorem 1.2 is a direct consequence of Theorem 1.1.

AcknowledgementsThe author sincerely thanks Professor Chungen Liu for his much precious help and valuable suggestions.The author is also most grateful to the referees for their careful reading and valuable suggestions.

[1]Ambrosetti,A.,Benci,V.and Long,Y.,A note on the existence of multiple brake orbits,Nonlinear Anal.TMA,21,1993,643–649.

[2]Bahri,A.and Berestycki,H.,Forced vibrations of superquadratic Hamiltonian systems,Acta Math.,152,1984,143–197.

[3]Benci,V.,Closed geodesics for the Jacobi metric and periodic solutions of prescribed energy of natural Hamiltonian systems,Ann.I.H.P.Analyse Nonl.,1,1984,401–412.

[4]Benci,V.and Giannoni,F.,A new proof of the existence of a brake orbit,in“Advanced Topics in the Theory of Dynamical Systems”,Notes Rep.Math.Sci.Eng.,6,1989,37–49.

[5]Bolotin,S.,Libration motions of natural dynamical systems(in Russian),Vestnik Moskov Univ.Ser.I.Mat.Mekh.,6,1978,72–77.

[6]Bolotin,S.and Kozlov,V.V.,Librations with many degrees of freedom(in Russian),J.Appl.Math.Mech.,42,1978,245–250.

[7]Chang,K.,In finite Dimensional Morse Theory and Multiple Solution Problems,Birkh¨auser Verlag,Basel,Boston,Berlin,1993.

[8]Ekeland,I.,Convexity Method in Hamiltonian Mechanics,Springer-Verlag,Berlin,1990.

[9]Ekeland,I.and Hofer,H.,Subharmonics of convex Hamiltonian systems,Comm.Pure Appl.Math.,40,1987,1–37.

[10]Ghoussoub,N.,Location,multiplicity and Morse indices of minimax critical points,J.Reine Angew Math.,417,1991,27–76.

[11]Gluck,H.and Ziller,W.,Existence of periodic solutions of conservtive systems,Seminar on Minimal Submanifolds,Princeton University Press 1983,65–98.

[12]Groesen,E.W.C.van,Analytical mini-max methods for Hamiltonian brake orbits of prescribed energy,J.Math.Anal.Appl.,132,1988,1–12.

[13]Hayashi,K.,Periodic solution of classical Hamiltonian systems,Tokyo J.Math.,6,1983,473–486.

[14]Li,C.and Liu,C.,Brake subharmonic solutions of first order Hamiltonian systems,Science in China Ser.A,53(10),2010,2719–2732.

[15]Li,C.and Liu,C.,Nontrivial solutions of superquadratic Hamiltonian systems with Lagrangian boundary conditions and the L-index theory,Chin.Ann.Math.Ser.B,29(6),2008,597–610.

[16]Liu,C.,Asymptotically linear Hamiltonian systems with Lagrangian boundary conditions,Pacific J.Math.,232(1),2007,233–255.

[17]Liu,C.,Maslov-type index theory for symplectic paths with Lagrangian boundary conditions,Adv.Non.Stu.,7,2007,131–161.

[18]Liu,C.,Minimal period estimates for brake orbits of nonlinear symmetric Hamiltonian systems,Discrete Contin.Dyn.Syst.,27,2010,337–355.

[19]Liu,C.,Subharmonic solutions of Hamiltonian systems,Nonlinear Anal.TMA,42,2000,185–198.

[20]Liu,C.and Zhang,D.,Iteration theory of L-index and multiplicity of brake orbits,J.Diff.Eq.,257,2014,1194–1245.

[21]Long,Y.,Index Theory for Symplectic Paths with Applications,Birkh¨auser Verlag,Basel,Boston,Berlin,2002.

[22]Long,Y.,Zhang,D.and Zhu,C.,Multiple brake orbits in bounded convex symmetric domains,Adv.in Math.,203,2006,568–635.

[23]McDuff,D.and Salamon,D.,Introduction to Symplectic Topology,Clarendon Press,Oxford,1998.

[24]Rabinowitz,P.H.,Minimax methods in critical point theory with applications to differential equations,CBMS Regional Conf.Ser.in Math.,65,AMS,RI,1986.

[25]Rabinowitz,P.H.,On the existence of periodic solutions for a class of symmetric Hamiltonian systems,Nonlinear Anal.TMA,11,1987,599–611.

[26]Rabinowitz,P.H.,On subharmonic solutions of Hamiltonian systems,Comm.Pure Appl.Math.,33,1980,609–633.

[27]Seifert,H.,Periodische Bewegungen mechanischer systeme,Math.Z.,51,1948,197–216.

[28]Silva,E.A.B.,Subharmonic solutions for subquadratic Hamiltonian systems,J.Diff.Eq.,115,1995,120–145.

[29]Szulkin,A.,An index theory and existence of multiple brake orbits for star-shaped Hamiltonian systems,Math.Ann.,283,1989,241–255.

[30]Zhang,D.,Minimal period problems for brake orbits of nonlinear autonomous reversible semipositive Hamiltonian systems,Discrete Contin.Dyn.Syst.,35(5),2015,2227–2272.