Grbner-Shirshov Bases of Irreducible Modules of the Quantum Group of Type G2∗
2016-06-09GhaniUSTAAbdukadirOBUL
Ghani USTA Abdukadir OBUL
1 Introduction
Reduction is a fundamental problem in studying the structures of algebras.Precisely,let A be an algebra given by a group of generators and a set of relations between them.We denote by S and?S?the set of these relations and the ideal generated by them,respectively.For any element a in S,we often need to decide whether a belongs to?S?or not.This is the so-called“membership problem”in algebra and it is often very difficult but important.
In his thesis[6],Buchberger provided a method to solve this problem in commutative algebra and called his theory the Gröbner bases theory.Later,Bergman[1]generalized Buchberg’s theory to associative algebra.On the other hand,Shirshov[18]developed the same theory for Lie algebras.In[2],Bokut proved that Shirshov’s method is also valid for associative algebras,so the theory of Shirshov for Lie algebras and the universal enveloping algebras is called the Gröbner-Shirshov bases theory.
In[5],Bokut and Malcolmson developed the Gröbner-Shirshov bases theory for the Drinfeld-Jimbo quantum groups and as an application,constructed a Gröbner-Shirshov basis for the quantum group of type An.Recently,in[14–16,19]the authors,by using the representation theory of algebras,constructed a Gröbner-Shirshov basis for the quantum groups of types G2,D4,E6,and F4.
In[12],Kang and Lee developed the Gröbner-Shirshov bases theory for the modules over associative algebras and in[13],by using their theory,constructed a Gröbner-Shirshov basis for the irreducible modules of simple Lie algebras of type An.Several years later,in[8]Chibrikov used another approach to deal with Gröbner-Shirshov bases for the modules,and the key idea in his approach is that a module of an algebra is viewed as a free module over a free algebra.Later,in[7],authors gave a Grbner-Shirshov basis for the modules over associative algebras by using the idea of Chibrikov.
In this paper,based on the Grbner-Shirshov basis for the Drinfeld-Jimbo quantum group Uq(G2)given in[16],we construct a Gröbner-Shirshov basis for the irreducible module Vq(λ)of Uq(G2)by using the method in[7]and by specializing a suitable version of Uq(G2)at q=1,we get a Gröbner-Shirshov basis for the universal enveloping algebra U(G2)of the simple Lie algebra of type G2and the finite-dimensional irreducible module V(λ)over it.And by comparing this new Gröbner-Shirshov basis for U(G2)with the one obtained in[3]we found that the new one contains the minimal basis in[3].
2 Some Preliminaries
For the convenience of the reader,in this section we recall some notions and results about the Gröbner-Shirshov bases of double-free modules and the quantum groups from[7],[9]and[11],respectively.
Let k be a field,X a non-empty set of letters with integer index,and X∗a free monoid of monomials in the letters in X.Let k?X?be the free associative k-algebra generated by X.In order to determine the leading term of an element f∈kwe choose a well ordering“<”on X∗,and then this ordering naturally induces an ordering in the free associative algebra kFor any element f∈kwe denote bythe leading term of f.If the coefficient of the leading term of f is 1,then we say f is monic.If f and g are two monic elements in k,and their leading terms areand g,then the composition of f and g are defined as follows.
(a)If there are a,b∈X∗such that==ω and the length ofthe number of the letters inis bigger than the length of b,then the composition of intersection is defined to be(f,g)ω=fa−bg.
(b)If there are a,b∈X∗such that==ω,then the composition of inclusion is defined to be(f,g)ω=f−agb.
Note that in both cases above,we have
Let S be a non-empty subset of kgenerated by some monic elements.We define a congruence relation with respect to S on kas follows:For any f,g ∈ k?X?and ω ∈ X∗,

where αi∈ k,ai,bi∈ X∗,si∈ S,andfor all i.If this is the case,then we say that f is congruent to g modulo S and ω,and denote it by f ≡ g mod(S;ω).If an element f is congruent to 0 modulo S for some ω,then we say f is trivial modulo S.If for any elements f,g ∈ S and ω ∈ X∗,the composition(f,g)ω,whenever it is defined,is trivial modulo S,then we say S is closed under composition.If S is not closed under composition,then we will need to expand S by attaching all nontrivial compositions(inductively)to S to obtain a completion Sc.We call Sc(if it is closed under composition,then S=Sc)a Gröbner-Shirshov basis for the ideal?S?of k?X?.Often,by abusing language,we call Sca Gröbner-Shirshov basis of k?X?.
Now we recall the definition of the double free module.
definition 2.1(see[8])Let X,Y be two sets,and modk?X??Y?a free left k?X?-module with the basis Y.Theny is called a double free module.
Let X,Y be two sets with well orderings and X∗Y={uy|u ∈ X∗,y ∈ Y}.For any ω ∈ X∗Y,we have a unique expression ω =x1···xny,where xi∈ X,i=1,···,n,y ∈ Y,n ≥ 0.Set

We define an ordering“≺”on X∗Y as follows:For any ω,´ω∈X∗Y,

where So the ordering“≺”is admissible. definition 2.2(see[7])Let S⊂modk?X??Y?be a non-empty subset generated by some monic elements,and “ ≺ ” the admissible ordering defined above.We say that S is a Gröbner-Shirshov basis in the free module modk?X?,if all compositions in S are trivial modulo S. The following is the composition-diamond lemma for the double free module,the central result about the Gröbner-Shirshov bases theory of the double free module. Lemma 2.1(see[8])Let S⊂modk?X?be a non-empty subset generated by some monic elements,and“≺”the admissible ordering defined above.The following statements are equivalent: (1)S is a Grbner-Shirshov basis of modk?X?Y; (2)If 0f∈kS,then=for some a∈X∗and s∈S; (2?)If 0?f ∈ kS,then f=αiaisiwith···,where αi∈ k,ai∈ X∗,si∈S; (3)Irr(S)is a k-linear basis for the factor module The following theorem explains the relation between the Gröbner-Shirshov bases of the associative algebra and the double free module. Theorem 2.1(see[7])Let X,Y be two sets with well orderings,“<”a monomial ordering on X∗and“≺”the admissible ordering defined above.Let S⊂kbe a subset generated by some monic elements.Then,S ⊂ kis a Gröbner-Shirshov basis of kif and only if SX∗Y ⊂is a Gröbner-Shirshov basis of modk?X?with respect to the ordering≺. Next,we recall some notions about quantum groups from[9]and[11]. Let k be a field and A=(aij)a symmetrizable n×n Cartan matrix,that is,an integer matrix with aii=2,aij0(i?j)and there is an integral diagonal matrix D=diag(d1,d2,···,dn)such that DA is a symmetric matrix,where d1,···,dnare non-negative integers.Let q be a nonzero element of k so that it is not a root of unity.The quantum group Uq(A)is a free k-algebra with generators{Ei,,Fi|1≤i,j≤n},subject to the relations for all 1≤i,j≤n and Letbe the subalgebras of Uq(A)generated byn},{Ei|1≤i≤n}and{Fi|1≤i≤n},respectively.Then we have the following triangular decomposition of the quantum group Uq(A): The following is the main result in[5]. Theorem 2.2 If the sets S+cand S−care the Gröbner-Shirshov bases ofandrespectively,then the set S+c∪K ∪T ∪S−cis a Gröbner-Shirshov basis of the quantum group Uq(A). From now on,we consider the quantum group Uq(G2).We choose the following orientation for G2 Then the corresponding Cartan matrix A and its minimal symmetrizer D are Let be the generating set of Uq(G2),where E1,E12,E122,E1222,E11222,E2are the modified images of the isomorphism classes of indecomposable representations of the species of type G2under the canonical isomorphism of Ringel between the corresponding Ringel-Hall algebra H(G2)and the positive part of the quantum groupare the images of the E1,E12,E122,E1222,E11222,E2under the convolution automorphism of the quantum group Uq(G2)(for details,see[16]).The following skew-commutator relations are computed in[16]: where i,j=1,2. The main result in[16]says that the set S of the above skew-commutator relations is a minimal Grner-Shirshov basis of the quantum goup Uq(G2).Note that the ordering induces a lexicographic ordering on the monomials of these generators. Now we are ready to construct a Gröbner-Shirshov basis for the irreducible modules of the quantum group Uq(G2).Let X∗be a free monoid generated by X,and Λ1,Λ2be fundamental weights.Let υλbe the highest weight vector with the highest weight λ,where λ =m1Λ1+m2Λ2and m1,m2are non-negative integers.The finite-dimensional highest weight Uq(G2)-module Vq(λ)with the highest weight λ generated by υλis defined to be(see definition 2.1): where S is a Grbner-Shirshov basis of Uq(G2)and(−,−)is the symmetrization of the Euler form(see[16]).From[10]we know that Vq(λ)is a finite-dimensional irreducible module,and any irreducible finite-dimensional module on Uq(G2)can be obtained in this way.Our main result is the following theorem. Theorem 3.1 The set is a Gröbner-Shirshov basis of the finite-dimensional irreducible Uq(G2)-module Vq(λ). Proof For convenience,we let where i=1,2. Now we prove that S1is closed under composition.Since S is a Gröbner-Shirshov basis of Uq(G2),we know from[7]that SX∗υλis closed under composition,and there is no composition between the elements ofSo we only need to prove that the compositions between the elements ofand SX∗υλare trivial. For any u=saυλ∈ SX∗υλ,s∈ S,a ∈ X∗, (I)if a?=1,then we consider the following three cases. (i)If SX∗υλ?u=sa1Eiυλ,where s ∈ S,a1∈ X∗,i=1,2, (ii)Ifs∈ S,a1∈ X∗,i=1,2,then there is no composition when 0 (iii)If SX∗υλ?u=sa1Kiυλ,where s ∈ S,a1∈ X∗,i=1,2,and s=s+t,t (II)if a=1,that is,u=sυλ∈ SX∗υλ,where s∈ S=S+∪K ∪T ∪S−,then we consider the following four cases. (i)If s∈S+,then s=ExEy,where Ex,Ey∈A,A={E12,E122,E1222,E11222}.Since we know from[17]that each E12,E122,E1222and E11222is polynomial of E1and E2without constant term,the proof is the same as(i)in(I). (ii)If s∈ S−,then by using the convolution automorphism(see[10])we convert this case to the case(i). (iii)If s∈K,then we have the following three compositions: If u=(KlKp−KpKl)υλ,where(l,p)>(p,l),when p=i,where i=1,2.So If u=when j=i.Thus SinceAgain,sincewe haveHence If uwhen l=i.So (iv)If s∈T,then there is no composition. The proof is complete. In order to specialize the quantum group Uq(G2)at q=1,we give another versionof Uq(G2)as follows. The k-algebrais generated bysubject to the relations where 1≤i,j≤2,and Then we have the following result. Theorem 3.2 The two k-algebrasare isomorphic. Proof We define two k-algebra homomorphisms φ and ψ as follows: and Then,we need to verify that these two maps are well-defined,that is,they are compatible with the defining relations for Uq(G2)and U?q(G2).Because of the definitions of φ and ψ,we only need to consider the relations relevant to Li.First,we prove that φ is well-defined.Since we have and φ is well-defined. Next,we prove that ψ is well-defined.Clearly, So Since one can get Similarly,we have So ψ is well-defined.Finally,we note that So Therefore,The proof is complete. This isomorphism gives the following Gröbner-Shirshov basis for where i,j=1,2. We denote this Grbner-Shirshov basis ofby S?.Moreover,by the isomorphism φ above,we define a(G2)-module structure on Vq(λ)as follows: and we denote this finite-dimensional irreducibleThen we get the following Gröbner-Shirshov basis for where X∗is the free monoid of monomials in the letters inWe denote bythe specialization ofBy using the Lie bracket and the formulas(6),(8),(13)and(15),we have From the formulas(1)–(5),(7),(9)–(12)and(14),we have In the same way,we have whereThen there is a surjection defined by and KerSo where U(G2)is the classical universal enveloping algebra of the simple Lie algebra of type G2.Hence by replacing the q and all Ki’s by 1 in the Gröbner-Shirshov basis S?of U?q(G2),and using the map f,we get the following Gröbner-Shirshov basis S0of U(G2): where i,j=1,2.In this Gröbner-Shirshov basis,we omit brackets for convenience.The Lie product[ab]will be written as(ab)or ab,[z1,z2···zm]will mean z1[z2···zm]and(z1z2···zm)will mean(z1z2···zm−1)zm.Thus,we have[z1z2···zm]=(−1)m−1zm···z2z1. In[4]a minimal Gröbner-Shirshov basis of U(G2)is given and by comparing it with the basis above,wefind that the minimal one is contained in the basis above. Again,by replacing the q and all Ki’s by 1 in the Gröbner-Shirshov basisof the finite-dimensional irreducible(G2)-module(λ)and using the map f,we get the following Gröbner-Shirshov basis of U(G2)-module V(λ): where X∗is the free monoid of monomials in the letters in{xi,hi,yi|1≤i≤2}.Note that here we have used the fact(λ,i)=mi,1 ≤ i≤ n(see[3]). AcknowledgementThe authors are grateful to the referee for the nice suggestions. [1]Bergman,G.M.,The diamond lemma for ring theory,Adv.Math.,29,1978,178–218. [2]Bokut,L.A.,Imbeddings into simple associative algebras,Algebra and Logic,15,1976,117–142. [3]Bokut,L.A.and Klein,A.A.,Serre relations and Grobner-Shirshov bases for simple Lie algebras I,II,Internat.J.Algebra Comput.,6,1996,389–400,401–412. [4]Bokut,L.A.and Klein,A.A.,Grbner-Shirshov bases for exceptional Lie algebras I,Journal of Pure and Applied Algebra,133,1998,51–57. [5]Bokut,L.A.and Malcolmson,P.,Grbner-Shirshov bases for quantum enveloping algebras,Israel Journal of Mathematics,96,1996,97–113. [6]Buchberger,B.,An Algorithm for Finding a Basis for the Residue Class Ring of a Zero Dimensional Polynomial ideal,Ph.D.Thesis,University of Innsbruck,Austria,1965. [7]Chen,Y.Q.,Chen,Y.S.and Zhong,C.Y.,Composition-diomond lemma for modules,Czechoslovak Math.J.,60,2010,59–76. [8]Chibrikov,E.S.,On free Lie conformal algebras,Vestnik Novosibirsk State University,4(1),2004,65–83. [9]Drinfel’d,V.G.,Hopf algebras and the quantum Yang-Baxter equation,Doklady Akademii Nauk SSSR,283(5),1985,1060–1064. [10]Jantzen,J.C.,Lectures on Quantum Groups,Graduate Studies in Mathematics,Vol.6,Amer.Math.Soc.,Providence,1996. [11]Jimbo,M.,A q-difference analogue of U(G)and the Yang-Baxter equation,Letters in Mathematical Physics,10(1),1985,63–69. [12]Kang,S.J.and Lee,K.-H.,Grbner-Shirshov basis for representation theory,J.Korean Math.Soc.,37(1),2000,55–72. [13]Kang,S.J.and Lee,K.-H.,Grbner-Shirshov bases for irreducible s?n+1-modules,J.Algebra,232,2000,1–20. [14]Obul,A.and Yunus,G.,Grbner-Shirshov basis of quantum group of type E6,J.Algebra,346,2011,248–265. [15]Qiang,C.X.and Obul,A.,Grbner-Shirshov basis of quantum group of type F4,Frontiers of Mathematics in China,9(1),2014,135–150. [16]Ren,Y.H.and Obul,A.,Grbner-Shirshov basis of quantum group of type G2,Comm.Algebra,39(5),2011,1510–1518. [17]Ringel,C.M.,PBW-bases of quantum groups,J.Reine Angew.Math.,470,1996,51–88. [18]Shirshov,A.I.,Some algorithmic problems for Lie algebras,Siberian Math.J.,3,1962,292–296. [19]Yunus,G.and Obul,A.,Gröbner-Shirshov basis of quantum group of type D4,Chin.Ann.Math.Ser.B,32(4),2011,581–592.




3 Grbner-Shirshov Bases of Irreducible Modules over the Quantum Group G2












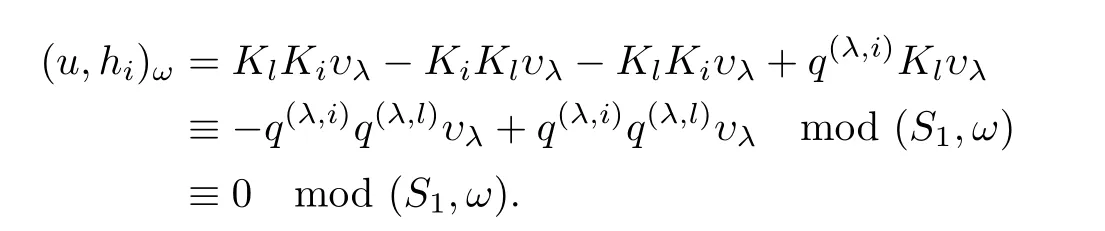





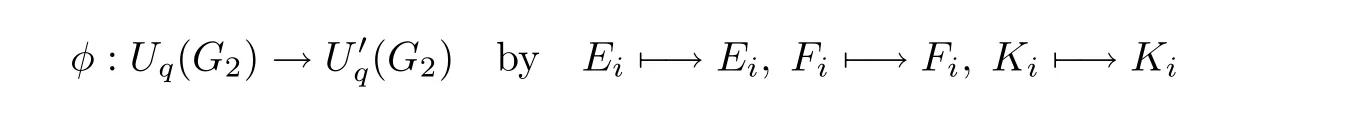
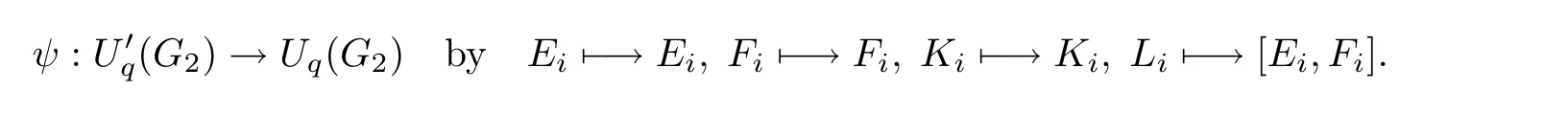







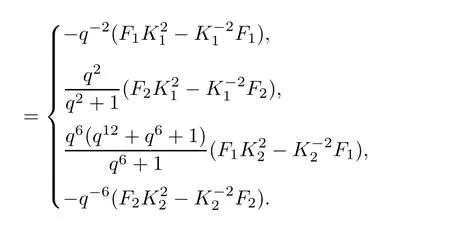















杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Initial Boundary Value Problem of an Equation from Mathematical Finance∗
- Twistor Spinors and Quasi-twistor Spinors∗
- The Riemann Problem with Delta Data for Zero-Pressure Gas Dynamics∗
- Adapted Metrics and Webster Curvature in Finslerian 2-Dimensional Geometry
- Brake Subharmonic Solutions of Subquadratic Hamiltonian Systems∗
- The Expansion of a Wedge of Gas into Vacuum with Small Angle in Two-Dimensional Isothermal Flow∗
