Twistor Spinors and Quasi-twistor Spinors∗

Yongfa CHEN

1 Introduction

It is well known that the spectrum of the Dirac operator on closed spin manifolds detects subtle information on the geometry and the topology of such manifolds(see[1]).The first sharp estimate for the nonzero eigenvalues λ of the Dirac operator is the well-known Friedrich inequality,which says that

where R is the scalar curvature of the closed spin manifold(Mn,g).The case of equality in(1.1)occurs if and only if(Mn,g)admits a nontrivial spinor field ψ called a real Killing spinor,satisfying the following overdetermined elliptic equation:

where X ∈ Γ(TMn)and the dot“.”indicates the Clifford multiplication.Obviously,a Killing spinor is a twistor spinor which is also an eigenspinor.The existence of Killing spinors implies severe restrictions on the manifold.The manifold must be a locally irreducible Einstein manifold and the simply connected manifolds admitting real Killing spinors were completely classified(see[2]).Some classification results for manifolds with twistor spinors can be seen in[3–4].

On the other hand,Lichnerowicz[5]and Hijazi[6]noticed that a manifold admitting a non-zero parallel k-form,for k?=0,n,carries no real Killing spinor.Furthermore,if(Mn,g)possesses a locally product structure,then there is no Killing spinor.Consequently,this shows the estimate(1.1)cannot be sharp,for example,on(quaternionic)K¨ahler manifolds,and on manifolds with a locally product structure.Indeed,better estimates have been proved in these cases by Kirchberg[7],Hijazi[8],Kramer et al[9],and Kim[10],respectively.

In the paper[8],K¨ahlerian twistor spinors are introduced to get lower bounds for the eigenvalues of the Dirac operator on closed spin K¨ahler manifolds.Hijazi also studied the uniqueness of K¨ahlerian twistor spinors and obtained some vanishing theorems(see[11]).In particular,he proved that on a K¨ahler spin manifold with R?≡0,the space of twistor spinors is reduced to zero.Motivated by the paper[8],we study the properties and applications of the quasi-Killing spinors and the quasi-twistor spinors which were used to get lower bounds for the eigenvalues of the Dirac operator in[10–12],and obtain some vanishing theorems.Especially,we prove that on a locally decomposable closed spin manifold with nonzero Ricci curvature,the space of twistor spinor is trivial.

The article is organized as follows:In Section 2,some geometric conventions and preliminaries are given.In Section 3,we discuss the quasi-Killing spinor and its application in lower bounds estimation for the eigenvalues of the Dirac operator.In the final section,the quasitwistor spinor is investigated.Especially,we give an integrability condition for twistor spinors(see Theorem 4.2).More generally,we study the uniqueness of quasi-twistor spinors on complete Riemannian spin manifolds(see Theorems 4.3–4.4).As a corollary,we know that on a locally decomposable closed spin manifold with Ric?≡0,the space of twistor spinors is trivial.

2 Preliminaries

Let(Mn,g)be an oriented n-Riemannian manifold.Let β be a(1,1)-tensor field on(Mn,g)such that β2= σId,σ = ±1 and

for all vector fields X,Y ∈ Γ(TMn)(here Id stands for the identity map).We say(Mn,g,β)is an almost Hermitian manifold if σ = −1 and an almost product Riemannian manifold if σ =1,respectively.Moreover,if σ = −1 and β is parallel,(Mn,g,β)is called a K¨ahler manifold.Similarly,we have the following definition.

definition 2.1(see[10,13])An n-Riemannian manifold(Mn,g)is called locally decomposable if it is an almost product Riemannian manifold(Mn,g,β)and β is parallel.

In case that(Mn,g,β)is locally decomposable,the tangent bundle TMndecomposes into TMn=T+Mn⊕T−Mnunder the action of the endomorphism β,where

Obviously,the distributions T±Mnare integrable since β is parallel.If(Mn,g)is simply connected and complete,then the De Rham decomposition theorem implies that there is a global splitting(Mn,g)=(M1×M2,g1+g2).

Example 2.1 Suppose that an n-Riemannian manifold(Mn,g)possesses a unit vector field ξ∈ Γ(TMn).Then the reflection β defined by is an almost product Riemannian structure.Moreover,it is a locally decomposable Riemannian structure if ξ is a parallel vector field.

We now suppose that(Mn,g)is a Riemannian manifold with a fixed spin structure.We understand the spin structure as a reduction SpinMnof the SO(n)-principal bundle of Mnto the universal covering Ad:Spin(n)→SO(n)of the special orthogonal group.The spinor bundle ΣMn=SpinMn×ρΣnon Mnis the associated complexdimensional complex vector bundle,where ρ is the complex spinor representation.The tangent bundle TMncan be regarded as TMn=SpinMn×AdRn.Consequently,the Clifford multiplication on ΣMnis the fibrewise action given by

On the spinor bundle ΣMn,one has a natural Hermitian metric,denoted as the Riemannian metric byThe spinorial connection on the spinor bundle induced by the Levi-Civita connection ∇ on Mnwill also be denoted by ∇.The Hermitian metricand spinorial connection ∇ are compatible with the Clifford multiplication μ.That is

∀φ,ϕ ∈ Γ(ΣMn)and ∀X,Y ∈ Γ(TMn).Using a local orthonormal frame field{e1,···,en},the spinorial connection∇,the Dirac operator D and the twistor operator P,are locally expressed as

respectively,which satisfy the following important relation:

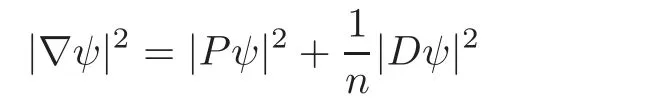
for any ψ ∈ Γ(ΣMn)(throughout this paper,the Einstein summation notation is always adopted).The kernels of the operators D and P are respectively,the twistor spinors and the harmonic spinors,and they are both conformally invariant.If M is closed,KerD=KerD2on L2(ΣMn).

Let RX,YZ?(∇X∇Y−∇Y∇X−∇[X,Y])Z be the Riemannian curvature of(Mn,g)and denote by RX,Yψ ?(∇X∇Y−∇Y∇X−∇[X,Y])ψ the spin curvature in the spinor bundle ΣMn.They are related via the formula

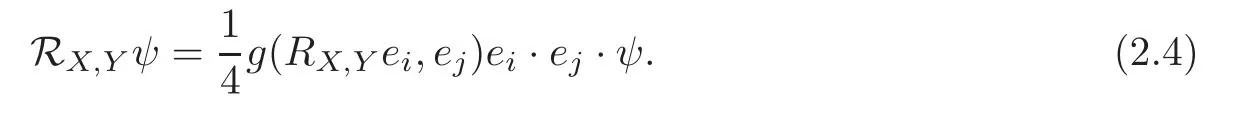
We also use the notation

andWith the help of the Bianchi identity,(2.4)implies

which in turn gives 2ei·ej·Rei,ejψ =Rψ.Hence one derives the well-known Schrödinger-Lichnerowicz formula

where∇∗is the formal adjoint of∇ with respect to the natural Hermitian scalar product on ΣMn.The formula shows the close relation between the scalar curvature R and the Dirac operator D.

On almost Hermitian manifolds or almost product Riemannian manifolds,we can also define the following β-twist Dβof the Dirac operator D by

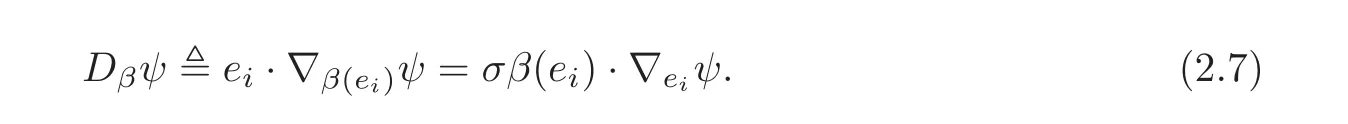
It is easy to see that Dβis a formally self-adjoint elliptic operator with respect to L2-product,if Mnis closed and divβ=0.As in the K¨ahlerian case,Kim obtained that D2=holds on the locally decomposable Riemannian spin manifold(Mn,g,β)(see Prop.2.1 in[10]).

3 Quasi-Killing Spinors

definition 3.1(see[10])A non-trivial solution ψ to the following field equation on the almost product Riemannian manifold(Mn,g,β)

is called a quasi-Killing spinor of type(a,b).

Obviously,if ψ is a quasi-Killing spinor of type(a,b),the energy-momentum tensor associated to ψ is given on the complement of its zero set by

for any X,Y ∈ Γ(TMn).Especially,the quasi-Killing spinor of type(a,0)(or β =±Id)is also called the generalized Killing spinor.In fact,in this case one can prove that the function a must be a constant.That is,ψ is in fact a Killing spinor.In addition,Hijazi proved that a manifold admitting a parallel 1-form carries no real Killing spinors(see[6]).Furthermore,we can prove the following theorem.

Theorem 3.1 Let ψ be a quasi-Killing spinor of type(a,b)on a locally decomposable Riemannian spin manifold(Mn,g,β),where β ?±Id.Then|ψ|2is a positive constant and

(1)if R?≡ 0,ψ is an eigenspinor of D,0a=b(or 0?a= −b)is constant,and R is a positive constant;

(2)if R≡0,then Ric≡0;

(3)the real vector field Xψdefined by

is a Killing field,i.e.,LXψg=0.

Proof(1)First,from

we know that ∇i|ψ|2=2Re?∇iψ,ψ?=0.Hence|ψ|2is a positive constant.One can also easily check

and

In particular

since=D2.Noting β±Id,we have a=±b,which in turn implies that β(∇a)=±∇a.Hence the quasi-Killing equation can also be written as

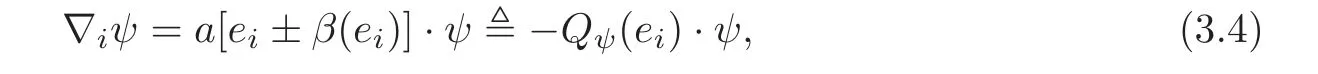
where Qψ=−a(Id±β).Moreover,by(2.5),

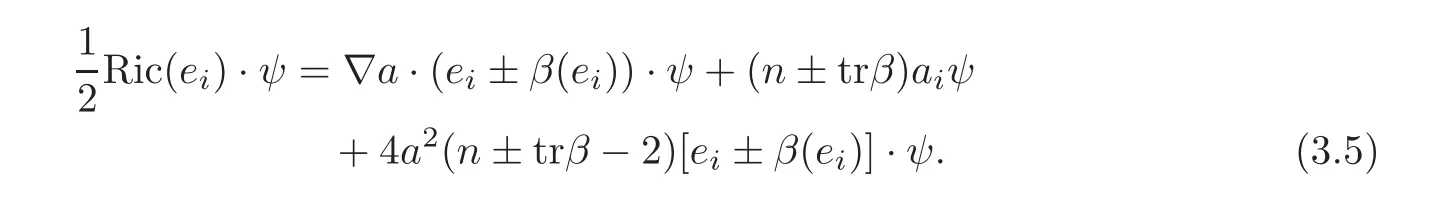
Hence performing its Clifford multiplication by eiyields

Using(trQψ)2=+|Qψ|2,it follows that

By dtrQψ=divQψ,we infer that

Consequently,∇a=0 since R is non-zero.Moreover,R is a positive constant andwhere n1dimT+Mn,n2dimT−Mn.

(2)If R ≡ 0,(3.7)yields a=0 or n±trβ−2≡ 0.If a=0,∇ψ=0 and Ric≡ 0.If n+trβ−2≡ 0,we see by(3.5)that

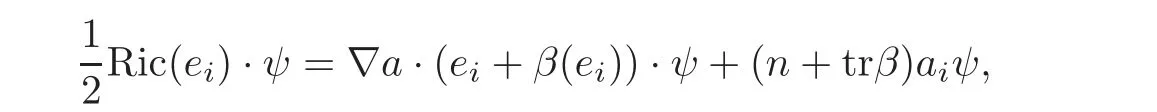
whereObviously

from which the result follows.

(3)Since the Clifford multiplication by vector fields is skew-symmetric with respect tothe vector field Xψis real.We need the following formula for arbitrary vector fields X,Y,Z∈Γ(TM)

since∇ is metric and torsion-free.On the other hand,by the definition of Xψ,at the point p with∇ei|p=0,

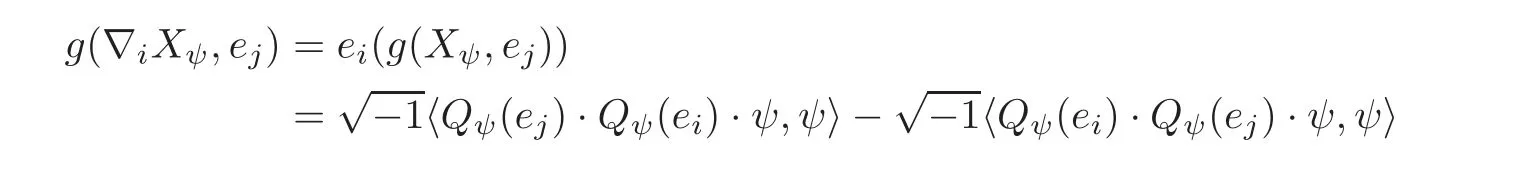
which is clearly skew-symmetric with respect to ei,ej.

Remark 3.1 We can compute if R?0 and Mnis closed,

Hence,Ric ≥ 0 and moreover,by the Bochner-Weitzenböck formula,we know that every harmonic 1-form on Mnis parallel.

One application of the quasi-Killing spinor is another simple proof of the following theorem,which is due to Alexandrov,Grantcharov and Ivanov[12].The other related issues can be seen in[10,14–15].

Theorem 3.2 Let(Mn,g),n≥3 be a closed Riemannian spin manifold of positive scalar curvature admitting a non-trivial parallel vector field of unit length.Then any eigenvalue λ of the Dirac operator D satisfies

The equality in(3.12)occurs if and only if there exists a quasi-Killing spinor field of type

Proof First suppose that ξ is a unit parallel vector field and let

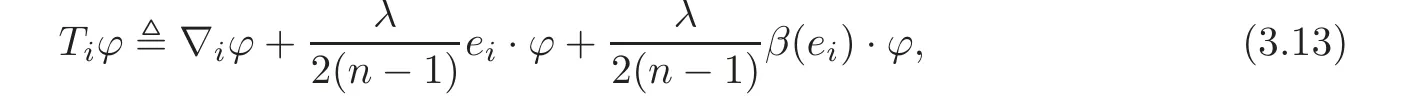
where Dϕ = λϕ, β(ei)?ei−2?ei,ξ?ξ.Then,an elementary calculation provides the following

At the same time,∇ξ=0 yields

Hence integrating(3.14)and applying the Schrödinger-Lichnerowicz formula(2.6),wefind that

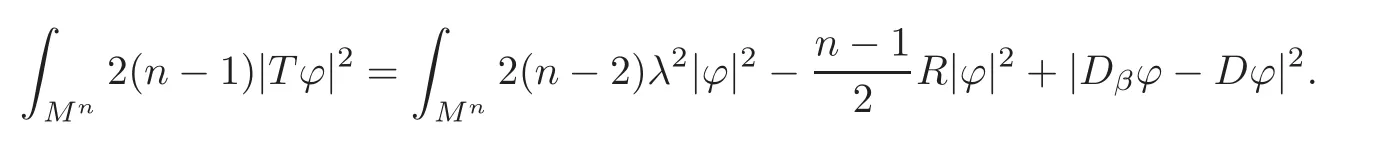
Note by the definition,

So using the Cauchy-Schwarz inequality leads to

From this,it follows immediately that

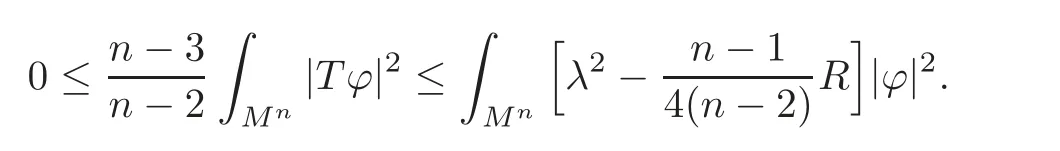
If λ2achieves its minimum,then Tϕ ≡ 0,which implies the associated eigenspinor ϕ is a nontrivial quasi-Killing spinor field on locally decomposable Riemannian spin manifold(Mn,g,β).

Remark 3.2 It follows from Tϕ ≡ 0, βij= δij− 2ξiξjthat

By Br’s result in[2],the universal covering space of the manifolds in the limiting case was described in[12].

Remark 3.3 The proof given above also works if ξ is just a harmonic vector field of unit length,and hence the result in[14]is also obtained.In fact,with the help of the Bochner-Weitzenböck formula on 1-forms,it is not difficult to check that for any φ,

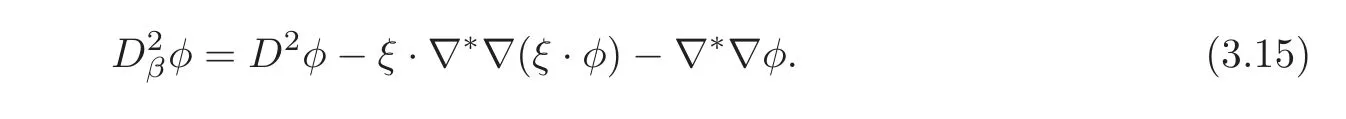
Note the fact that ξ is a harmonic vector field of unit length implies div(β)=0,hence Dβis self-adjoint with respect to L2-product.Hence

So,if Dφ=λφ,one can use the classical Rayleigh inequality and(2.6)to conclude

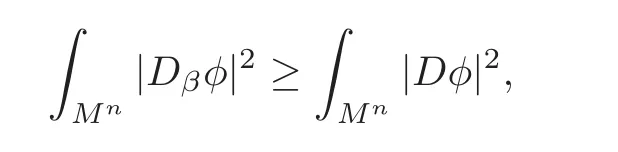
and the remaining proof is quite similar to that of Theorem 3.2.

4 Quasi-twistor Spinors

Analogous to the K¨ahlerian twistor equation in[8],we have the following definition.

definition 4.1(see[10])A non-trivial solution ψ to the following field equation on almost product Riemannian manifold(Mn,g,β):

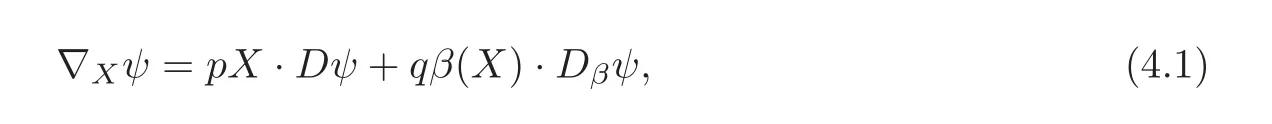
is called a quasi-twistor spinor of type(p,q),where p,q∈R.

Remark 4.1 Obviously,the quasi-twistor spinor of type(−,0)is the familiar twistor spinor or called conformal Killing spinor which lies in the kernel of the twistor operator P(see(2.3)).

On a locally decomposable spin manifold,a straightforward computation using(4.1)gives the following-Ric formula(see[10])

and the following useful identity

Theorem 4.1 Suppose that ψ is a quasi-twistor spinor of type(p,q)on a locally decomposable Riemannian spin manifold(Mn,g,β), β ?±Id and Dψ = λψ,where λ ?0.Then

Proof(1)If trβ=0,then from0 and

one gets

(2)then the limiting-case in Friedrich’s inequality is achieved,and moreover,Mncarries a nontrivial Killing spinor with a real nonzero Killing number.Hence Mnis locally irreducible,which is a contradiction(see[16]).

(3)If trβ?0 and pq?0,we know

HenceConsequently,ψ is a quasi-Killing spinor.

Now we turn to discuss the existence of twistor spinors.It is well-known that

if n≥3,and the maximal possible dimension is attained only for conformal flat manifolds as in the case of conformal Killing fields.Furthermore,Hijazi proved that on a K¨ahler spin manifold with R?0,the space of twistor spinors is reduced to zero(see[8]).Another proof of this result can also been seen in[11].Here,we prove the following theorem.

Theorem 4.2 Suppose that(Mn,g)is a closed Riemannian spin manifold admitting a non-trivial harmonic vector field ξ,ψ is a non-trivial twistor spinor.Then on Mnthe following integrability condition holds:

where D(Ric)(ξ)?ei·(∇iRic)(ξ).

Proof Let ψ be a non-trivial twistor spinor,i.e.,

which implies the following integrability conditions

and

Hence from(4.6),

First,the harmonicity of the vector field ξ= ξiei,together with the compactness of Mn,implies that

This means that ξi,j= ξj,iand ξi,i=0,respectively.Moreover,

On the one hand,

and on the other hand,

Therefore(4.8)turns into

From(4.5),(4.7)and(4.10)–(4.11),it is clear that

Hence the proof of the theorem is completed.

Remark 4.2 Note

and any non-trivial twistor spinor on a spin manifold vanishes at most at one point(see[5]).So taking the inner product of(4.4)with ξ·ψ and comparing its real part,we obtain on Mn,

which is also a corollary of the well-known fact that the Einstein tensoris divergence-free.

As an immediate consequence of the preceding theorem,we obtain the following corollary.

Corollary 4.1 Suppose a closed Riemannian spin manifold admits a non-trivial parallel vector field and R?≡0,and then the space of twistor spinors is trivial.

Proof Suppose ξ is a unit parallel vector field,and we denote the dual one-form of ξ also by ξ.Since

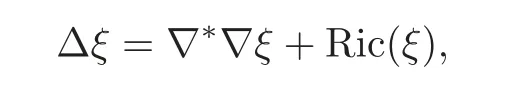
it follows that Ric(ξ)=0.Hence the theorem above implies

for any non-trivial twistor spinor ψ.Eventually,wefind that R ≡ constant ≥ 0,since all eigenvalues of D2are non-negative on closed spin manifolds.Hence(4.7)implies that the limiting-case in Friedrich’s inequality is achieved,and moreover,(Mn,g)is Einstein with R ≥ 0.In fact,ψ is the sum of two non-parallel real Killing spinors,or ψ is parallel(in this case R ≡ 0),which is a contradiction.

Corollary 4.2 Suppose spin manifold(Mn,g)is a closed Riemannian symmetric space with b1(M)?0 and R?0,and then the space of twistor spinors is trivial.

Remark 4.3 In fact,from the proof of the theorem above one can easily see that if a(not necessarily closed)Riemannian spin manifold admits a non-trivial unit parallel vector field and R?≡ 0,∇R ·ψ =nξ(R)ξ·ψ still holds for any non-trivial twistor spinor ψ.So R must be a constant(≤0).

Now we return to studying the uniqueness of quasi-twistor spinors.

Theorem 4.3 Let ψ be a quasi-twistor spinor of type(p,q)on a locally decomposable complete Riemannian spin manifold(Mn,g,β),β?= ±Id.Then

(1)If∇R?0,then

(2)If R is a nonzero constant and ψ ∈ L2(ΣMn),we also havehere n1dimT+Mn,and n2dimT−Mn.

Proof(1)First,assume∇R?=0.From

we obtain

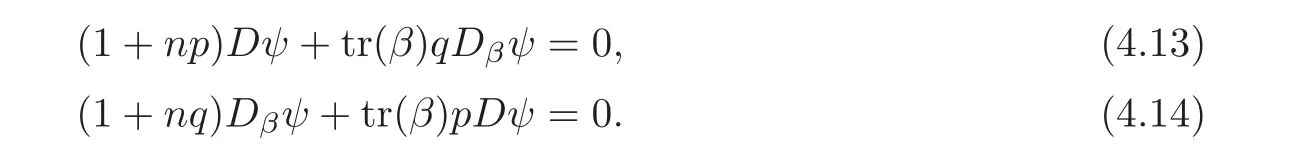
Noting R0,we also have

and

Note0 and

That is

If ψ(m)?0,it follows from(4.18)that

Suppose now ψ(m)=0.Since ψ is a solution of the elliptic differential equation

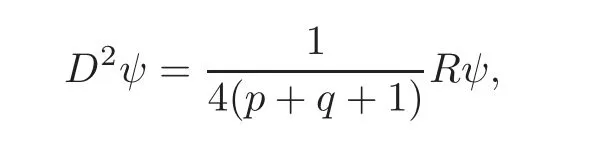
there exists a sequence of points miconverging to m such that ψ(mi)?=0.Then we have(1+np)∇R+tr(β)qβ(∇R)=0 at points miand with respect to the continuity of ∇R and β(∇R).We obtain again(1+np)∇R(m)+tr(β)qβ(∇R)(m)=0.Hence from(4.18),using β2=Id,one gets the system

Similarly,from(4.19),we obtain

Hence,if∇R+β(∇R)?=0 and∇R?=0,then from(A)and(B)

Note

So

Hence solving the linear equations above leads to

and Dψ =Dβψ.Moreover,Dψ for i≤n1and∇jψ =0 for j>n1.

If∇R+β(∇R)=0 and∇R?=0,then∇R−β(∇R)?=0.Moreover,from(A)and(B),

A similar argument shows that

and Dψ=−Dβψ.

(2)Now suppose that R is a nonzero constant and ψ ∈ L2(ΣMn).Hence D2ψ ∈ L2(ΣMn)by(4.2).Note for the L2-norm?·?and any number t>0,we have(see[17,p.96])

which implies that Dψ ∈ L2(ΣMn).Therefore we know that ψ lies in the domain of the maximal extension of D.Since Mnis complete,D is essentially self-adjoint as an unbounded operator in L2(ΣMn),so the maximal and the minimal extensions coincide and ψ ∈ dom()=dom(D∗).

On the other hand,by combining(4.13)and(4.14)wefind that

Therefore by integrating(4.24)and using=D2,one obtains

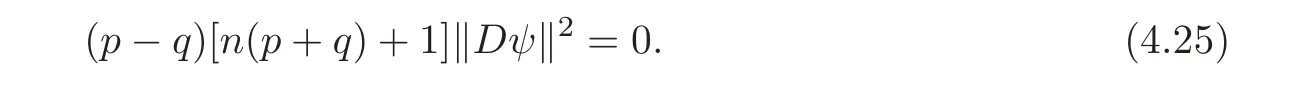
Case 1 If

Case 2 If p=q,then(4.15)implies that

Case 3 SupposeThen

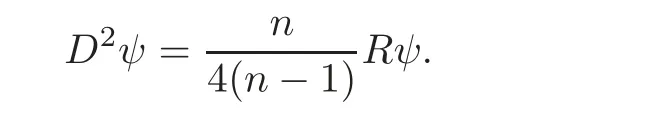
Clearly,R is a positive constant.Hence Mncarries a non-parallel real Killing spinor,which is a contradiction.

Obviously,from the proof of the above theorem,one gets the following theorem.

Theorem 4.4 Let ψ be a quasi-twistor spinor of type(p,q)on a locally decomposable closed Riemannian spin manifold(Mn,g,β),β?=±Id.Then

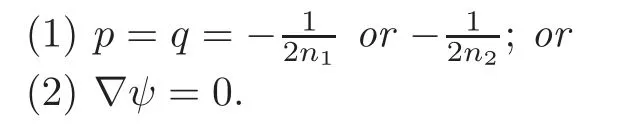
Remark 4.4 When Dψ=λψ,Kim and Alexandrov classify all the types of spin manifolds admitting non-trivial quasi-twistor spinors of type

Corollary 4.3 On a locally decomposable closed Riemannian spin manifold with β ?±Id and Ric?0,the space of twistor spinors is trivial.

AcknowledgementThe author cordially thanks the referees for their careful reading and helpful comments.

[1]Lawson,H.B.and Michelsohn,M.L.,Spin Geometry,Princeton Math Series,38,Princeton University Press,Princeton,1989.

[2]B¨ar,C.,Real Killing spinors and holonomy,Comm.Math.Phys.,154,1993,509–521.

[3]Lichnerowicz,A.,Killing spinors,twistor-spinors and Hijazi inequality,J.Geom.Phys.,5,1988,2–18.

[4]KÜhnel,W.and Rademacher,H.B.,Asymptotically Euclidean manifolds and twistor spinors,Comm.Math.Phys.,196,1998,67–76.

[5]Lichnerowicz,A.,Spin manifolds,Killing spinors and the universality of the Hijazi inequality,Lett.Math.Phys.,3,1987,331–344.

[6]Hijazi,O.,A conformal lower bound for the smallest eigenvalue of the Dirac operator and Killing spinors,Commun.Math.Phys.,104,1986,151–162.

[7]Kirchberg,K.D.,An estimation for the first eigenvalue of the Dirac operator in closed K¨ahler manifolds of positive scalar curvature,Ann.Glob.Ann.Geom.,3,1986,291–325.

[8]Hijazi,O.,Eigenvalues of the Dirac operator on compact K¨ahler manifolds,Comm.Math.Phys.,160(3),1994,563–579.

[9]Kramer,W.,Semmelmann,U.and Weingart,G.,Eigenvalue estimates for the Dirac operator on quaternionic K¨ahler manifolds,Math.Z.,230,1999,727–751.

[10]Kim,E.C.,Lower bounds of the Dirac eigenvalues on compact Riemannian spin manifolds with locally product structure.arXiv:math.DG/0402427

[11]Kirchberg,K.D.,Properties of K¨ahlerian twistor spinors and vanishing theorems,Math.Ann.,293(2),1992,349–369.

[12]Alexandrov,B.,Grantcharov,G.and Ivanov,S.,An estimate for the first eigenvalue of the Dirac operator on compact Riemannian spin manifold admitting a parallel one-form,J.Geom.Phys.,28,1998,263–270.[13]Yano,K.and Kon,M.,Structures on Manifolds,World Sci.,Singapore,1984.

[14]Alexandrov,B.,The first eigenvalue of the Dirac operator on locally reducible Riemannian manifolds,J.Geom.Phys.,57(2),2007,467–472.

[15]Moroianu,A.and Ornea,L.,Eigenvalue estimates for the Dirac operator and harmonic 1-forms of constant length,C.R.Math.Acad.Sci.Paris,338,2004,561–564.

[16]Br,C.,Spectral bounds for Dirac operators on open manifolds,Ann.Glob.Anal.Geom.,36,2009,67–79.

[17]Friedrich,T.,Dirac operators in Riemannian geometry,Graduate Studies in Mathematics,25,American Mathematical Society,Providence,RI,2000.

[18]Hijazi,O.,Lower bounds for the eigenvalues of the Dirac operator,J.Geom.Phys.,16,1995,27–38.