Adapted Metrics and Webster Curvature in Finslerian 2-Dimensional Geometry

Mircea CRASMAREANU

1 Introduction

The present note introduces the Webster scalar curvature discussed by Chern and Hamilton in[5]into the framework of 2-dimensional Finsler geometry.More precisely,we compute the Webster curvature for the sphere bundle T1S of a Finsler surface(S,F(x,y))by using the structural equations of this bundle.Specifically,the condition of adapted metric of[5]is suitable for only one 1-form(namely ω3)of the natural co-frame of T1S endowed with the Sasaki type metric gSasakiinduced by F.This condition,called vertical adapted,reduces the discussion to the Riemannian surfaces by the vanishing of the main scalar I and yields the constant Gaussian curvature K=2.It follows that the Webster curvature is12and a natural Cartan structure(in terms of[8,p.148])is given by the horizontal 1-forms.Let us remark that an interplay between Cartan structures and the generalized Finsler structures is studied in[13–14].

We apply this computation to prove a structure result,that is,T1S with gSasakiis homothetic with a generalized Berger sphere.More precisely,we obtain that under the vertical adapted condition,the vector field e3,dual of ω3with respect to gSasaki,is a Killing vector field for this metric and then it makes(gSasaki,ω3)a Sasakian structure on T1S.Another important result is that in our setting ω3is a pseudo-Hermitian form corresponding to a CR structure on T1S.Although this pseudo-Hermitian structure is non-Einstein,we obtain that its Webster scalar curvature is again12.

In order to extend the class of metrics,we generalize the concept of adapted metrics;in fact,we modify the original condition of Chern-Hamilton from the scalar 2 to a general ρ∈R in order to cover all possibilities;this approach was used in[6].Also our study is enlarged to all 1-forms providing the natural co-frame of T1S.

2 Webster Scalar Curvature:The Chern-Hamilton Formalism

Fix(M3,g)to be a 3-dimensional Riemannian manifold and consider{ω1,ω2,ω3}as an orthonormal basis of 1-forms on M;then M is oriented with the volume form ω1∧ ω2∧ ω3.Then there exists a unique skew-symmetric matrix of 1-forms

such that the structural equations

hold on M.Making one step further,we derive the existence of the functions{Kij;1≤i,j≤3}such that Kij=Kjiand

Recall that the subject of[5]consists in adapted metrics for a contact 1-form ω,i.e.,Riemannian metrics satisfying

If g is adapted to ω3,then the Webster scalar curvature W of the triple(M,g,ω3)is defined as

and is computed in[5]for the unit sphere S3,the unit tangent bundle of a compact orientable surface of genus g?1(for g=0 it results in W=1)and the Heisenberg group Nil3.In fact,W(S3)=1 and W(Nil3)=0.For another formalism on Webster curvature,see[3,p.212]and our formula(5.4)below.

A last main notion of this note is that of Cartan structure according to definition 1.1 of[8,p.148]:A pair of 1-forms ω1,ω2with

3 Finsler 2-Dimensional Geometry and Adapted Metrics

Let S be a 2-dimensional manifold and π :TS → S its tangent bundle.Let x=(xi)=(x1,x2)be the local coordinates on S and(x,y)=(xi,yi)=(x1,x2,y1,y2)the induced local coordinates on TS.Denote by O the null-section of π.

Recall that a Finsler fundamental function on S is a map F:TS→R+with the following properties:

(F1)F is smooth on the slit tangent bundle TSO and continuous on O;

(F2)F is positive homogeneous of degree 1:F(x,λy)= λF(x,y)for every λ >0;

(F3)the matrixis invertible and its associated quadratic form is positive definite.

The tensor field(gij(x,y))is called the Finsler metric.

Due to the homogeneity condition,all important objects of Finsler geometry actually live on the sphere bundle p:T1S={(x,y)∈TS;F(x,y)=1}→S(see[2,p.9]).Here T1S is 3-dimensional and an adapted co-frame consists in three 1-forms denoted by ω1,ω2,ω3.More precisely,after[2,p.93],we have

where g=det(gij),being the canonical nonlinear connection of the Finsler geometry(S,F)(see[2,p.34]).The vector fieldsspan the vertical distribution whilespan the horizontal distribution.The Finsler metric yields the Sasaki type metric on T1S(see[2,p.93]):

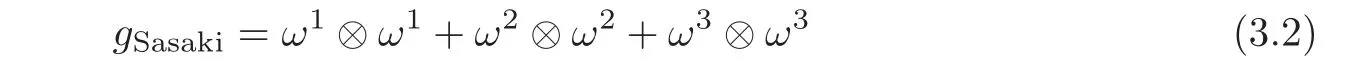
making{ω1,ω2,ω3}an orthonormal co-frame.If{e1,e2,e3}is the dual frame,then e1and e2are horizontal while e3is vertical.

After[2,p.82],the structural equations of(S,F)are

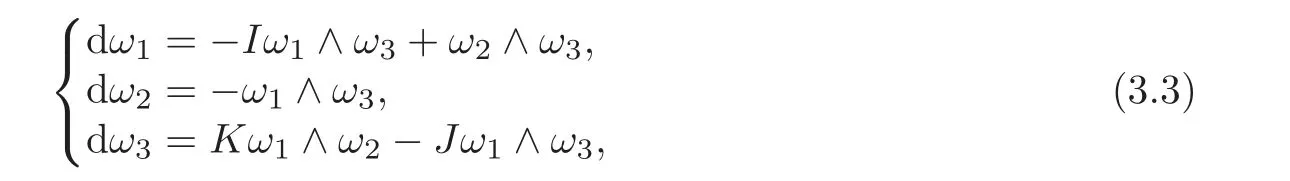
where I,J,K are smooth functions defined as follows(see[2,p.82]):

(i)I is the Cartan(or main)(pseudo-)scalar.Its vanishing characterizes Riemannian surfaces,i.e.,g=g(x)which means thaton TS is exactly the Sasaki lift of the Riemannian metric g.It also follows thatbeing the Christoffel symbols of g.

(ii)J is the Landsberg(pseudo-)scalar.Its vanishing characterizes Landsberg surfaces.

(iii)K is the Gaussian curvature.Its vanishing characterizes flat(in the Finslerian sense)surfaces.Note that ω3is a contact form for non- flat Finslerian surfaces since ω3∧ dω3=ω3∧(Kω1∧ω2−Jω1∧ω3)=Kω1∧ω2∧ω3.Then e3can be called the Reeb vector field of(S,F).

Remark that Bianchi equations yield some relations between these functions(see[2,p.97]):

where the subscript i denotes the derivation in the direction of ei,i.e.,df=f1ω1+f2ω2+f3ω3.It follows that I=0 implies J=0 and also K2=0.

In order to enlarge the class of suitable metrics,we consider the following notion which appears(with a factor 2 in RHS)in[11].

definition 3.1 Fix a 1-form ω on a general(M3,g)and the real number ρ.The Riemannian metric g on M is called ρ-adapted to ω if dω = ρ ∗ ω.

We conclude from(3.3)the following proposition.

Proposition 3.1 The metric gSasakianis

(i)1-adapted to the ω1if and only if S is a Riemannian surface;

(ii)1-adapted to ω2;

(iii)K-adapted to ω3in the Landsberg case.

It follows that the lift of the round metric of S2to T1S2=RP3=SO(3)is 1-adapted all ω’s.

4 Webster Curvature in Finslerian Geometry of Surfaces

Comparing(2.3)with(3.3),it results that gSasakican be an adapted metric only for ω3,in which case we say that it is vertical adapted due to the character of the Reeb vector field e3;correspondingly the 1-forms ω1,ω2will be called horizontal.We are ready for the main result of this note.

Theorem 4.1 The Riemannian metric gSasakiof T1S is vertical adapted if and only if S is a Riemannian surface with K=2.Then,the horizontal pair(ω1,ω2)is a Cartan structure and the Webster curvature is

Proof Since ωiis a gSasaki-orthonormal co-frame,we have ∗ω3= ω1∧ ω2,and locking at(3.33),we get that gSasakiis vertical adapted if and only if J=0,K=2.From the second Bianchi relation(3.4),we deduce that I=0,which yields the first part of the conclusion.

Now,the structural equations have the expression

and then we get the relations(2.5)with ω1∧dω1= ω2∧dω2= ω1∧ω2∧ω3=being the volume form of the metric gSasaki.It also follows that

It results in

which gives the matrix of K’s:

all other being zero.Using the definition(2.4),it results in the Webster curvature(4.1).

Remark 4.1(i)Comparing our result with the second example of[5,p.285]gives that Kiigiven by(4.5)coincides with relations(22)of the cited paper for?=12=W.

(ii)If S is compact embedded in R3(being also oriented),then a classical sphere theorem(from 1897)of Hadamard states that S must be diffeomorphic with a sphere.The following Theorem 4.2 clarifies this claim.

(iii)In[7],the 1-form η =Iω3is introduced under the name Cartan-type form of(S,F)and it is proved that η ∧ dη is the Chern-Simons form of(S,F).In our setting,this Chern-Simons form is zero.

(iv)A Cartan structure is a particular case of taut contact circle according to the definition 1.1 of[8,p.148]and then any linear combination λ1ω1+λ2ω2with(λ1,λ2)∈ S1⊂ R2defines the same volume form,and in our case that is the form of gSasaki.

As an application of the previous theorem,we have the following structural result.

Theorem 4.2 If the Riemannian metric gSasakiof T1S is vertical adapted,then the manifold(T1S,gSasaki)is Sasakian and homothetic with a generalized Berger sphere.

Proof According to the classification of[9,p.124],W=12implies that if(T1S,gSasaki,ω3)is a Sasakian manifold,then it is homothetic with a generalized Berger sphere.Hence we must prove that the vertical adapted condition implies the Sasakian condition for gSasaki.But from[3,p.87],we know that in dimension 3 this is equivalent to the cu K-contact condition and then we prove that the vertical adapted condition implies that e3is a Killing vector field for gSasaki.

According to[4,p.28],we have the general Lie brackets:

which yields the Levi-Civita connection of gSasaki:

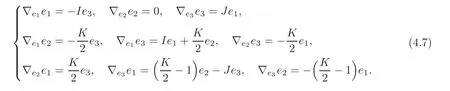
Let X=Xieiand Y=Yieibe two arbitrary vector fields on T1S,we get

It follows that the Lie derivatives of the metric are

The vertical adapted condition gives then

and we have the final conclusion.

Remark 4.2(i)The relations in first line of(4.7)yield that under the vertical adapted condition all vector fields eiare geodesic:∇eiei=0.Also,we can determine the generalized Berger sphere structure of(T1S2,gSasaki)according to the computations of[12].More precisely,we consider SU(2)=S3with the natural left-invariant and orthonormal frame(X1,X2,X3)of[12,p.7],and gSasakiis the metric making orthonormal the frame:as in[12,p.81].

(ii)Let us remark that our contact structure on T1S is different from that of[3,p.175]for which the K-contact condition is characterized via the well-known Tashiro theorem([3,p.178])in terms of constant curvature+1 for the base manifold(S,g(x)).Let us also note that the Finslerian version of the Tashiro theorem was proved in[1].

(iii)Our Theorem 4.2 is a particular case of Lemma A.1 of Alan Weinstein from the Appendix of[5]that ϕ1= ω1, ϕ2= ω2implies e3is a Killing vector field.Also,from the complex structural equations(39)of[5,p.290],it follows that Ω = ω1+iω2is a closed differential 1-form:dΩ=0.

5 An Associated Pseudo-Hermitian Structure on T1S

From the third equation of(4.8),it results that the vertical adapted condition implies

and recall,after[3,p.87],that the Sasakian condition reads

in terms of the structural tensor field φ of(1,1)-type.It gives the expression of φ:

Let D=kerω3be the structural distribution associated to ω3.A second formula for the Webster scalar formula is[3,p.213]:

where τ is the scalar curvature of the metric g and Ric(e3)is the Ricci curvature in the direction of e3.Note also that in the same way as[3,p.214],we have where K(D)is the sectional curvature of the 2-plane D and from Theorem 7.1 of[3,p.112]on the 3-dimensional K-contact case it results that Ric(e3)=2.Using the Levi-Civita connection(4.7),we obtain K(D)= −1,so then τ=2 and from(4.14)we arrive again at W=

Remark also that J=φ|Dis a complex structure satisfying the integrability conditions:

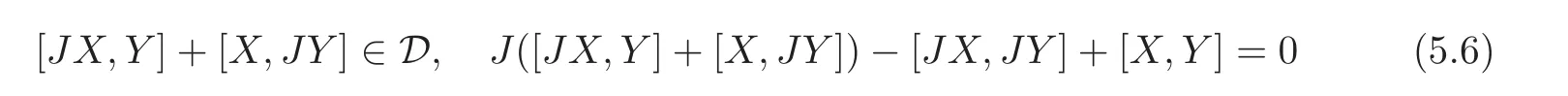
for all X,Y∈D=span{e1,e2}.Using the terminology of[10],ω3is a pseudo-Hermitian structure on the CR manifold(T1S,D,J).Its associated Webster metric:

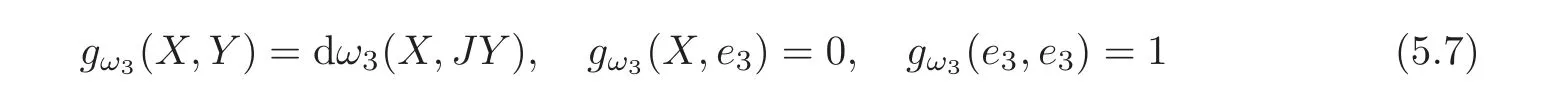
being

is not positive definite and hence the pseudo-Hermitian structure is not strictly pseudoconvex.Since the Levi-Civita connection of gω3satisfies

it results that

and then,as in the previous section,we get that e3is a Killing vector field for gω3,which means that e3is a transversal symmetry(see[10,p.446])for the given pseudo-Hermitian structure.

Using the formulae of[10,p.448]we get a component of the Webster-Ricci tensor of gω3:

and then the Webster scalar curvature of gω3is

Since we have RicW?= −iscalWdω3,it results that this pseudo-Hermitian structure is not Einstein.

AcknowledgementThe author is extremely indebted to an anonymous referee who helped to substantially improve the presentation and the contents of this paper.

[1]Anastasiei,M.,A framed f-structure on tangent manifold of a Finsler space,An.Univ.Bucure¸sti Math.Inform.,49(2),2000,3–9.

[2]Bao,D.,Chern,S.-S.and Shen,Z.,An introduction to Riemann-Finsler geometry,Graduate Texts in Mathematics,200,Springer-Verlag,New York,2000.

[3]Blair,D.E.,Riemannian geometry of contact and symplectic manifolds,2nd edition,Progress in Mathematics,203,Birkh¨auser Boston,Inc.,Boston,MA,2010.

[4]Bryant,R.L.,Finsler structures on the 2-sphere satisfying K=1,in “Finsler Geometry” (Seattle,WA,1995),27–41,Contemp.Math.,196,Amer.Math.Soc.,Providence,RI,1996.

[5]Chern,S.-S.and Hamilton,R.S.,On Riemannian Metrics Adapted to Three-Dimensional Contact Manifolds,with an Appendix,by Alan Weinstein,Lecture Notes in Math.,1111,Workshop Bonn,1984,279–308,Springer-Verlag,Berlin,1985.

[6]Crasmareanu,M.,Adapted metrics and Webster curvature on three classes of 3-dimensional geometries,International Electronic Journal of Geometry,7(2),2014,50–59.

[7]Feng,H.and Li,M.,Adiabatic limit and connections in Finsler geometry,Comm.Anal.Geom.,21(3),2013,607–624.arXiv:1207.1552

[8]Geiges,H.and Gonzalo,J.,Contact geometry and complex surfaces,Invent.Math.,121(1),1995,147–209.

[9]Guilfoyle,B.S.,The local moduli of Sasakian 3-manifolds,Int.J.Math.Math.Sci.,32(2),2002,117–127.[10]Leitner,F.,On transversally symmetric pseudo-Einstein and Fefferman-Einstein spaces,Math.Z.,256(2),2007,443–459.

[11]Nicolaescu,L.I.,Adiabatic limits of the Seiberg-Witten equations on Seifert manifolds,Comm.Anal.Geom.,6(2),1998,331–392.

[12]Petersen,P.,Riemannian Geometry,2nd edition,Graduate Texts in Mathematics,171,Springer-Verlag,New York,2006.

[13]Sabau,S.V.,Shibuya,K.and Shimada,H.,Moving frames on generalized Finsler structures,J.Korean Math.Soc.,49(6),2012,1229–1257.

[14]Sabau,S.V.,Shibuya,K.and Pitis,Gh.,Generalized Finsler structures on closed 3-manifolds,Tohoku Math.J.(2),66(3),2014,321–353.