基于双惩罚分位回归的面板数据模型理论与实证研究

罗幼喜 ，李翰芳，田茂再， 郑 列

(1.湖北工业大学理学院，湖北 武汉，430068；2.湖北工业大学产品质量工程研究院，湖北 武汉，430068；3.华中师范大学数学与统计学学院，湖北 武汉，430079；4.中国人民大学统计学院，北京，100872)



基于双惩罚分位回归的面板数据模型理论与实证研究

罗幼喜 ，李翰芳，田茂再， 郑 列

(1.湖北工业大学理学院，湖北 武汉，430068；2.湖北工业大学产品质量工程研究院，湖北 武汉，430068；3.华中师范大学数学与统计学学院，湖北 武汉，430079；4.中国人民大学统计学院，北京，100872)

固定效应和随机效应同时选择是面板数据模型研究中的重要问题之一。本文通过分别对固定效应和随机效应引入条件Laplace先验，提出了一种新的贝叶斯双惩罚分位回归法。该方法不仅能对模型中重要解释变量进行自动选择，而且充分考虑到个体随机波动对解释变量系数估计带来的偏差。通过对方差分量的惩罚压缩，减少了模型中未知参数的个数，提高了模型自由度。Monte Carlo模拟及实证分析显示，所提出的方法不仅能准确估计出固定效应系数，而且能精确地捕捉到个体随机效应的波动。

面板数据；分位回归；贝叶斯分析；固定效应；随机效应；变量选择；Laplace 先验

面板数据模型是统计分析中应用最广泛的模型之一，其数据间不仅允许存在相关性，还可以带有异方差。将个体扰动看作是随机效应而引入模型，提高了面板数据模型的精度和建模的灵活性。如何将分位回归方法引入到面板数据模型研究中以克服传统建模方法的不足已成为这些年来的研究热点。Koenker[1]针对纵向数据采用了带惩罚的分位回归方法，即在极小化损失函数的同时对个体固定效应实施L1范数惩罚；Farcomeni等[2]研究了纵向生存数据的分位回归模型；Lamar-che[3]、Kato等[4]考虑了面板数据在多个分位点同时极小化检验函数的L1范数惩罚法，而Galvao[5]、Chernozhukov等[6]对动态面板数据模型也采用了类似的研究方法，虽然模拟显示此方法在非正态分布情形下要优于传统的均值回归方法，但惩罚参数难以确定是该方法的一个缺点。

随着近几年各领域高维复杂数据的出现，变量选择成了面板数据建模的一个重要课题。选择合适的预测变量子集不仅有助于提高模型精度，也能够在实际问题中获得更好的解释，所以如何同时估计和选择重要的固定效应和随机效应是面板数据模型研究的热门和难点问题。常见方法是假定随机效应结构不变而只考虑固定效应的选择。模型选择准则如AIC、BIC等虽然可以用来比较一系列被择模型，但当预测变量增加时，被择模型的数量将会呈几何级数增长。为减少计算量，Jiang等[7]提出一个替代的两步选择法，然而其自身的不连续性使得模型选择结果不稳健。Bondell等[8]利用Cholesky 分解提出一种同时选择固定效应和随机效应的方法，其虽然能够在一定程度上减少计算量，但难以向其它形式的损失函数扩展，尤其是对应于分位回归的损失函数。

对于普通的线性分位回归模型，Li等[9]构造了与多种惩罚相等价的贝叶斯正则化方法，随后李翰芳等[10]、李子强等[11]将该正则化方法推广到含随机效应的面板数据模型中。然而，这些方法都只考虑了固定效应的选择。本文则通过分别对固定效应和随机效应引入条件Laplace先验，提出一种新的贝叶斯双惩罚分位回归法。该方法不仅能对模型中重要解释变量进行自动挑选，而且充分考虑到个体随机波动对解释变量估计带来的偏差，通过对方差分量的惩罚压缩，可减少模型中未知参数的个数，提高模型自由度。

1 模型与方法

首先建立面板数据的条件分位回归模型，然后给出参数估计的贝叶斯双惩罚法。

对于响应变量Y，这里考虑其给定分位点τ时的条件分位回归函数：

(1)

式中：QY(τ|xit,zit,αi)=inf{y∶F(y|xit,zit,αi)≥τ}为Y的τ(0<τ<1)分位数；xit为个体i在时刻t 时的k维解释变量；βτ是对应的回归系数向量；αiτ是个体i的p维随机效应向量；zit是对应的p维协变量。

假设响应变量yit具有非对称 Laplace 分布(ALD)，在αi给定的条件下模型(1)样本的似然函数为

(2)

式中：y=(y11,y12,…,y1T,y21,…,yNT)′；ρτ(u)=u(τ-I(u≤0))。由于是考虑给定分位点τ时β和αi的估计，故下文中省略参数下标τ。

由于ALD分布没有共轭先验，本文利用文献[12]中对ALD分布的正态和指数分解，将模型(1)等价表示为：

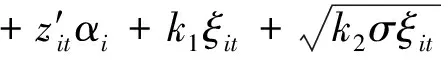
i=1,…,N；t=1,…,T

(3)

与常见的正态先验不同的是，为了同时对模型中重要固定效应和随机效应系数进行选择，在此设β、α分别有条件Laplace先验：

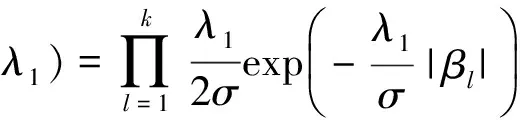
(4)

通过似然函数式(2)可以获得β、α、σ的后验密度：

π(β,σ,α|y,λ1,λ2)∝L(β,σ|y,α,τ)·

(5)

若视σ为厌恶参数，则极大化式(5)等价于极小化下式：

(6)

式(6)可以看成是一种对β、α同时施加Lasso惩罚的双惩罚分位回归方法。

2 参数估计的MCMC算法

在给定Laplace先验信息下，直接从式(5)中获得β、α的估计较为困难，利用等式

(7)

可以构造出所有未知参数的一种简单MCMC(Markov Chain Monte Carlo)抽样算法，具体构造方法如下。

(8)

令S=(s1,…,sk)，从而有

(9)

(10)

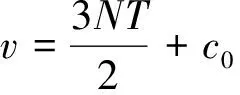
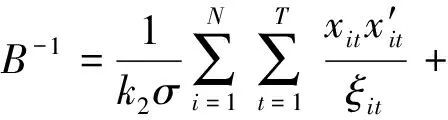
(10)将每次上一步抽取的数据值代入下一步生成新的数据，重复步骤(2)(9)直至收敛。

3 计算机模拟分析

下面通过Monte Carlo模拟来对本文提出的贝叶斯双Lasso惩罚分位回归估计(BLLQR)与文献[13]中的贝叶斯分位回归估计(BQR)、文献[10]中的贝叶斯Lasso分位回归估计(BLQR)、文献[11]中的贝叶斯Adaptive Lasso分位回归估计(BALQR)在重要自变量及随机效应选择上的表现进行比较。

模拟数据由以下面板数据模型生成：

i=1,…,N；t=1,…,T

(11)

由表1可见，对于固定效应系数的估计，采用本文提出的BLLQR方法所得MSE值及其标准差均最小，表明该方法整体估计精度和稳定性均最优。从具体每个参数的估计来看：

(1)对于模型中两个非零且受到随机效应干扰的参数β0和β1，BQR的估计偏差最小，BLLQR与BALQR的估计精度相当，BLQR的最差。这一点不难理解，因为这两个系数在模型中的原始设置即为非0的重要系数，而BLQR、BALQR及BLLQR却均对其进行了压缩，虽然BALQR在大样本情况下能够获得无偏估计，但在有限的模拟样本中则难以达到。BLQR和BLLQR由于采用的都是普通Lasso惩罚，从而偏差更大一些，但BLLQR比BLQR的偏差要小。虽然在偏差上BLLQR不是最优的，但BLLQR的标准差最小，原因是此模型中还设置有部分随机效应的干扰，BLLQR是4种方法中唯一考虑了随机效应选择的方法，从而其排除干扰的能力更强一些。

(2)对于模型中非零且未受到随机效应干扰的参数β2，BLLQR的估计偏差和标准差均最小，其次为BQR，而BLQR则表现最差。故可以看出，对于模型中的非零系数，虽然采用Lasso惩罚会带来一定的偏差，但如果能够正确识别出是否有随机效应的干扰，则能对估计偏差有一个更大幅度的修正，BQR方法虽然不会有压缩偏差，但其无法识别随机效应存在与否，将所有系数都按照有非零随机效应干扰对待，从而带来了估计偏差。

表2 4种方法在极端分位点处的估计结果比较(τ=0.9)

(3)对于模型中本身为零且未受到随机效应干扰的参数β3，3种对系数进行了压缩的方法BLQR、BALQR和BLLQR明显优于BQR，其中BLLQR无论是在偏差还是在标准差上均是最优的，从而可以看到，与普通的只能对固定效应进行选择的单惩罚方法BLQR、BALQR相比，本文提出的双Lasso惩罚法BLLQR能够有效对模型中固定效应与随机效应进行同时选择和估计。

另外，对于随机效应的非零方差参数φ1和φ2，4种方法的估计效果相当，但对于误将其包含在模型中的零方差参数φ3和φ4，BLLQR估计则明显优于其它3种方法。BLLQR基本能够将这些冗余的随机效应排除在模型之外，可见本文提出的双Lasso惩罚法BLLQR无论对模型中真实存在的随机效应还是错误假设的随机效应都能够进行较为精确的识别与估计。这一点对于实际数据建模极为有利，因为建模前往往不知道具体有哪些固定效应应该保留在模型之中，也不知道哪些固定效应系数受到了随机效应的影响，从而通常会假定所有固定效应和随机效应都存在。一方面，如果估计方法不能自动排除冗余解释变量，则整体估计精度就会降低，尤其是在冗余解释变量较多时更是如此，如BQR法；另一方面，如果估计方法不能自动排除冗余随机效应，则对于实际并不存在的随机效应均会估计过高，从而也会影响参数的整体估计精度，如BLQR和BALQR法。

从表2来看，4种方法在极端分位点处的估计精度和稳定性均比在中位点处的差一些，这与普通的分位回归估计类似，其主要原因是极端分位点处的样本点较为稀疏，从而估计精度会有所降低。与中位点处的情况类似，BLLQR估计的MSE均值和标准差都是最小的，即固定效应系数整体估计最优。对于每个具体的固定效应系数，BLLQR在β2及β3上的估计偏差和标准差均是最优的，尤其是对于固定效应系数为0且不受随机效应干扰的β3，其估计效果远远优于其它方法。而对于方差分量的估计，BLLQR对于不为0的方差参数估计精度与其它3种方法相当，对于本身为0的方差参数，其估计值也与0极为接近。

4 实证分析

本文考虑利用贝叶斯双惩罚分位回归法来探讨几个重要宏观经济指标对GDP的影响程度，这几个宏观经济指标既包括影响GDP的3个内在因素：总固定资产投资总额 (Finvest)、城镇居民全年平均消费性支出(Consume)和进出口总额 (Imexport)，也包括影响GDP的3个外在因素：财政支出 (Finac)、外商直接投资 (FDI)和R&D经费支出 (R&D)。共收集了1998—2013年30个省市地区(西藏自治区数据缺失较多略去)的面板数据，数据来源于《中国统计年鉴 (1999—2014)》。为了便于后面对各个因素的影响进行比较，所有数据均取对数后再进行标准化处理。

由于各个地区经济发展水平极不平衡，本文考虑如下随机系数的面板数据模型：

GDPit=(β0+αi0)+(β1+αi1)Finvestit+

(β2+αi2)Finacit+(β3+αi3)FDIit+

(β4+αi4)Imexportit+(β5+αi5)R&Dit+

(β6+αi6)Consume+εit,

i=1,…,30；t=1,…,16

(12)

在上述模型中，先假设每个指标的系数都受到截面个体随机效应αip(p=0,1,2,…,6)的影响。虽然对于有些经济发展水平相当的省市，这一随机效应差异可能并不显著，但由于本文提出的贝叶斯双惩罚分位回归法能够自动地对重要固定效应和随机效应进行选择，所以该假设并不影响本方法对模型中各个参数作出正确的估计。取τ=0.25、0.5、0.75分别计算3个分位点处的估计结果，在每次估计中，为了使抽样值达到稳定状态，所有算法均迭代40 000次，并保留后20 000次抽得的样本来获得参数点估计和置信区间估计，结果如表3所示。

表3 贝叶斯双惩罚分位回归法在3个分位点处的估计结果

从表3中可以看到，各个指标对GDP的影响权重有着较为显著的差别，而且这种差别随着分位点的不同也在发生改变。首先，从不同分位点处来看，低分位点τ=0.25时，总固定资产投资额 (Finvest) 、财政支出 (Finac)和进出口总额 (Imexport)3个变量权重系数占据主导地位，其它3个变量即外商直接投资 (FDI) 、R&D经费支出和城镇居民全年平均消费性支出(Consume)的权重系数都很小，0均包含在这3个指标系数的95%置信区间内，说明其在5%水平下并不显著；在中位点τ=0.5处，除总固定资产投资额 (Finvest) 、财政支出 (Finac)和进出口总额 (Imexport)外，城镇居民全年平均消费性支出(Consume)在模型中也变得显著；在高分位点τ=0.75处，模型中的显著性变量又增加了R&D经费支出指标。综合来看，总固定资产投资额 (Finvest)、财政支出 (Finac)和进出口总额 (Imexport)这3个指标无论在哪个分位点处权重系数都显著且排在前位，说明我国经济总量对这几个指标的依赖度还很高。从各个分位点处指标重要程度排名变化情况来看，城镇居民全年平均消费性支出(Consume)变化最大，从低分位点处的不显著跃升至高分位点处的权重系数最大，可见扩大消费对GDP快速增长有着很大的拉动效应。另外，R&D经费支出也从低分位点处的不显著变为高分位点模型中的显著变量，说明科技创新对于经济的稳定增长也逐渐起着不可忽视的作用。

从表3中还可以看到，对于各个影响指标，随着分位点的增加，总固定资产投资额 (Finvest)、 财政支出 (Finac)和进出口总额 (Imexport)系数是逐渐变小的，而城镇居民全年平均消费性支出(Consume)、R&D经费支出权重系数均是逐渐增大的，也即要使得GDP能够长期持续增长，则需要降低经济增长对政府投资的依赖度，着重扩大消费内需以及增加科技研发创新的投入力度，这也给当前经济结构调整及转型提供了重要的启示。

5 结论

(1)本文提出的BLLQR贝叶斯双惩罚分位回归估计由于同时考虑到了固定效应与随机效应的选择，故其无论是在中位点处还是在极端分位点处的总体表现在参与比较的4种方法中均是最优的。

(2)3种对固定效应系数进行了压缩的方法BLQR、BALQR、BLLQR在非重要解释变量的排除能力上都要明显优于BQR法，而且本文提出的BLLQR法对未受随机效应干扰的非零固定效应系数的估计精度甚至优于BQR法。

(3)对于模型中重要解释变量系数的估计，本文提出的BLLQR法也都能够给出较为精确的估计，在参与比较的4种方法中估计的标准差均是最小的，也即估计性能最为稳健。另外，由于BLLQR法也可以通过切片Gibbs抽样算法在专门的统计分析软件WinBUGS中实现，所以待估参数虽然较BQR、BLQR和BALQR中的参数多，但在计算时间消耗上并无明显差别。

[1] Koenker R. Quantile regression for longitudinal data[J].Journal of Multivariate Analysis,2004,91:74-89.

[2] Farcomeni A, Viviani S. Longitudinal quantile regression in the presence of informative dropout through longitudinal-survival joint modeling[J]. Statistics in Medicine, 2015,34(7): 1199-1213.

[3] Lamarche C. Robust penalized quantile regression estimation for panel data[J]. Journal of Econome-trics, 2010,157(2):396-408.

[4] Kato K, Galvao A F, Montes-Rojas G V. Asymptotics for panel quantile regression models with individual effects[J]. Journal of Econometrics, 2012,170(1): 76-91.

[5] Galvao A F. Quantile regression for dynamic panel data with fixed effects[J]. Journal of Econometrics, 2011,164(1):142-157.

[6] Chernozhukov V，Fernandez-Val I，Hahn J, et al. Average and quantile effects in nonseparable panel models[J].Econometrica, 2013,81(2): 535-580.

[7] Jiang J, Rao J S. Consistent procedures for mixed linear model selection[J]. Sankhy: The Indian Journal of Statistics, 2003,65(1): 23-42.

[8] Bondell H D, Krishna A, Ghosh S K. Joint variable selection for fixed and random effects in linear mixed-effects models[J]. Biometrics, 2010,66:1069-1077.

[9] Li Qing, Xi Ruibin, Lin Nan. Bayesian regularized quantile regression[J]. Bayesian Analysis, 2010, 5(3):533-556.

[10]李翰芳, 罗幼喜, 田茂再. 面板数据的贝叶斯Lasso分位回归方法[J].数量经济技术经济研究, 2013(2): 138-149.

[11]李子强, 田茂再, 罗幼喜. 面板数据的自适应Lasso分位回归方法研究[J].统计与信息论坛, 2014, 29(7): 3-10.

[12]Kozumi H, Kobayashi G. Gibbs sampling methods for Bayesian quantile regression[J]. Journal of Statistical Computation and Simulation, 2011,81:1565-1578.

[13]Luo Youxi, Lian Heng, Tian Maozai. Bayesian quantile regression for longitudinal data models[J]. Journal of Statistical Computation and Simulation, 2012,82:1635-1649.

[责任编辑 尚 晶]

Theoretical and empirical study on panel data models based on double penalized quantile regression

LuoYouxi1，2，LiHanfang1，3，TianMaozai4，ZhengLie1，2

(1. School of Science, Hubei University of Technology, Wuhan 430068, China;2. Institute of Product Quality, Hubei University of Technology, Wuhan, 430068, China;3. School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China;4. School of Statistics, Renmin Univiesity of China, Beijing 100872, China)

It is an important issue to select fixed and random effects simultaneously for panel data models. This paper proposes a new Bayesian double penalized quantile regression method by introducing the conditional Laplace prior both for fixed and random effect parameters. This method can not only select the important explanatory variables in the model automatically but also give a full consideration to the biases of parameter estimation for explanatory variables which are produced by individual random fluctuations. By applying shrinkage to the variance components, the number of unknown parameters in the model is reduced, thus the model’s freedom degree is enhanced greatly. Monte Carlo simulation and empirical study indicate that the proposed method can accurately estimate the fixed effect parameters and catch the exact fluctuation of individual random effects.

panel data; quantile regression; Bayesian analysis; fixed effect; random effect; variable selection; Laplace prior

2016-09-08

国家自然科学基金资助项目(11271368)；教育部人文社会科学研究青年基金资助项目(13YJC790105)；湖北工业大学博士科研启动基金资助项目(BSQD13050).

罗幼喜(1979-)，男，湖北工业大学副教授，博士.E-mail：youxiluo@163.com

O212；F064.1

A

1674-3644(2016)06-0462-06