二维矩形条带装箱问题的离散化左下角定位模型

李 明,张曼曼 ,亓晓莹 ,唐秋华

(1.武汉科技大学理学院,湖北 武汉，430065;2.武汉科技大学机械自动化学院,湖北 武汉，430081)



二维矩形条带装箱问题的离散化左下角定位模型

李 明,张曼曼 ,亓晓莹 ,唐秋华

(1.武汉科技大学理学院,湖北 武汉，430065;2.武汉科技大学机械自动化学院,湖北 武汉，430081)

分别针对不旋转和可旋转两种情况下的离散化二维矩形条带装箱问题(2DR-SPP)，采用各矩形的左下角坐标对矩形的放置点进行定位，建立了两个整数线性规划模型。采用GAMS/CPLEX软件对标杆算例进行求解，验证了所建模型的有效性和准确性。

二维装箱问题;离散化；定位模型;整数规划

二维矩形条带装箱问题(2D rectangular strip packing problem, 简称2DR-SPP)是指将给定的若干个矩形互不重叠地装入给定宽度、长度无限的矩形条带箱中，使得箱子被矩形所占用的长度最短。2DR-SPP是在板材切割、布料裁剪和木材加工等领域普遍存在的一个问题，对此问题的建模与求解有重要的理论研究价值。

目前，对2DR-SPP的研究主要集中于求解算法。Hifi[1]利用分支定界算法对中小规模2DR-SPP 进行了有效求解。Burke等[2]针对正交2DR-SPP，提出一种最优匹配(best-fit)启发式算法，根据当前部分解的状态选择具有最佳适应度的矩形放置解，此外该算法还在求解的不同阶段运用不同的处理策略以减少求解时间。Chen等[3]提出一种双阶段启发式搜索算法求解2DR-SPP，首先根据普通占角规则选择放置位置，然后根据全局适应度对其进行评价并选择最佳位置。Cui等[4]将递归结构和分支定界策略相结合，提出一种启发式递归分支定界算法。张德富等[5]基于砌墙规则提出一种启发式算法，可有效求解规模较大的算例。蒋兴波等[6]首先提出一种含五种启发式规则的底部左齐择优匹配算法，然后将此算法与遗传算法相结合，得到了精度更高的解。Leung等[7]提出一种基于层的快速启发式算法。彭碧涛等[8]提出一种迭代启发式算法，采用矩形装载适应度计算规则和树型迭代搜索规则，选择最高适应度的矩形置入箱内。黄岚等[9]将遗传算法和离散粒子群算法相融合，提出一种混合算法求解矩形排样问题。Chen等[10]提出一种融合了启发式算法、局部搜索算法和demon算法的混合算法。此外，Yang等[11]还针对2DR-SPP提出了一种简单的随机搜索算法。

与求解算法相比，对2DR-SPP建模方面的研究较少。于洪霞等[12]针对不可旋转2DR-SPP建立了非线性规划理论模型。Castro等[13]基于矩形左下角端点坐标建立了二维矩形装箱问题的混合整数规划模型，其借助一种特殊的连续辅助变量控制矩形的重叠行为，可有效求解矩形不旋转情形下的2DR-SPP，而对可旋转情形只是给出了问题的理论模型。

本文对文献[13]中的模型进一步改进，针对不旋转和可旋转两种情形建立2DR-SPP的纯整数线性规划模型，并借助GAMS/CPLEX软件对标杆算例进行求解，以检验所建模型的有效性和准确性。

1 问题描述

假设2DR-SPP中矩形的宽度和高度以及条带箱的宽度值都为整数。记矩形的序号集合为I，I={i|i=1,…,|I|}，矩形i的高度和宽度分别为hi和li，条带箱的宽度为L。

当矩形要求以不旋转方式分配至条带箱中时，上述问题称为不旋转2DR-SPP。此时由于矩形的高度和宽度固定，且放置方式唯一，故矩形所占条带箱的行和列位置可由其左下角单元位置唯一确定，由此所建立的数学模型称为2DR-SPP的离散化不旋转左下角定位模型。

2 离散化不旋转左下角定位模型

定义0-1决策变量xijk和辅助变量zijk(i∈I,j∈J,k∈K)，其中当矩形i的左下角单元占用箱子的单元(j,k)时xijk=1，否则xijk=0；当矩形i占用箱子的单元(j,k)时zijk=1，否则zijk=0。

对于矩形i，由于其列数(或行数)为li(或hi)，所以其左下角单元不能被置于箱子的第L-li+2,…,L列和第|J|-hi+2,…,|J|行，否则该矩形将从列或行的方向溢出箱子(列溢出情形见图1)，所以要满足

xijk=0,∀i∈I,(j,k)∈(Ω-Ωi)

(1)

式中：Ω={(j,k)|j∈J,k∈K}为箱子的单元区域，Ωi={(j,k)|j≤|J|-hi+1,k≤L-li+1,j∈J,k∈K}为矩形i左下角单元的可放置区域。

图1 矩形列溢出和未溢出两种情形示例

Fig.1 Two examples with and without rectangle columnoverflow

矩形i的左下角单元在其可放置区域Ωi中必须且仅占有一个单元，即要满足

,∀i∈I

(2)

约束条件式(1)和式(2)可保证任意一个矩形i的左下角单元(j,k)占且仅占用其可放置区域Ωi的一个单元，并保证矩形的所有单元不会溢出箱子。下面利用另一变量zijk保证各矩形的所有单元都被不重叠地置于箱子中。

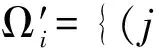
图2 矩形左下角单元和其它单元的关系示意图

Fig.2 Relationship between left bottom corner and the other elements of a rectangle

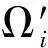
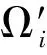
(3)

约束条件式(3)可保证矩形i的所有单元都被置于箱子中，但无法保证箱子的某个单元被多个矩形占用。

为了防止矩形的单元在条带箱中发生重叠，即防止箱子中存在单元格被至少2个或以上矩形占用，增加以下约束：

≤1,∀j∈J，k∈K

(4)

引入变量N表示箱子被矩形占用的行数，对目标线性化得式(5)和式(6)。

min N

(5)

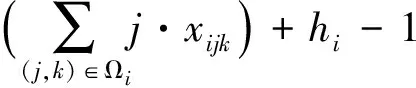
(6)

此外，由于所有矩形都必须被置入箱内，所以根据所有矩形的单元总数和箱子列数的关系，可得箱子所需的最小单元行数，即理论最优值为：

此理论最优值可为优化目标中的最小行数N进行定界，以减小问题的可行解空间，即有

N≥N1

(7)

3 离散化可旋转左下角定位模型

当矩形可旋转放置时，它所占条带箱的行数和列数不仅取决于该矩形的高度和宽度，也取决于其放置方式，即不旋转放置还是旋转90°放置。

在已有0-1变量xijk的基础上，增加新的0-1变量yi(i∈I)，定义yi=1表示矩形i不旋转放置，yi=0表示矩形旋转90°放置。

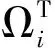
xijk≤(1-yi),∀i∈I，(j,k)∈(Ω-Ωi)

(8)

(9)

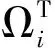
,∀i∈I

(10)

对条带箱的任意一个单元(j,k)，约束式(11)可保证所装的矩形不会发生重叠。

≤1,∀j∈J，k∈K

(11)

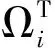
综合考虑两种情形可建立相应约束如下：

zij′k′≥xijk-(1-yi),

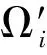
(12)

zij*k*≥xijk-yi,

(13)

基于式(5)和式(6)，构建可旋转情形下二维矩形条带装箱问题的优化目标如下：

min N

(14)

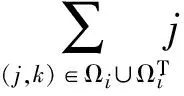
∀i∈I

(15)

此外，当矩形i的行数hi超出箱子的列数L时，必须不旋转放置，即yi=1 ，于是有

≤yi

(16)

而当矩形i的列数li超出箱子的列数L时，则必须旋转放置，即yi=0，相应要满足

≤1-yi

(17)

4 算例

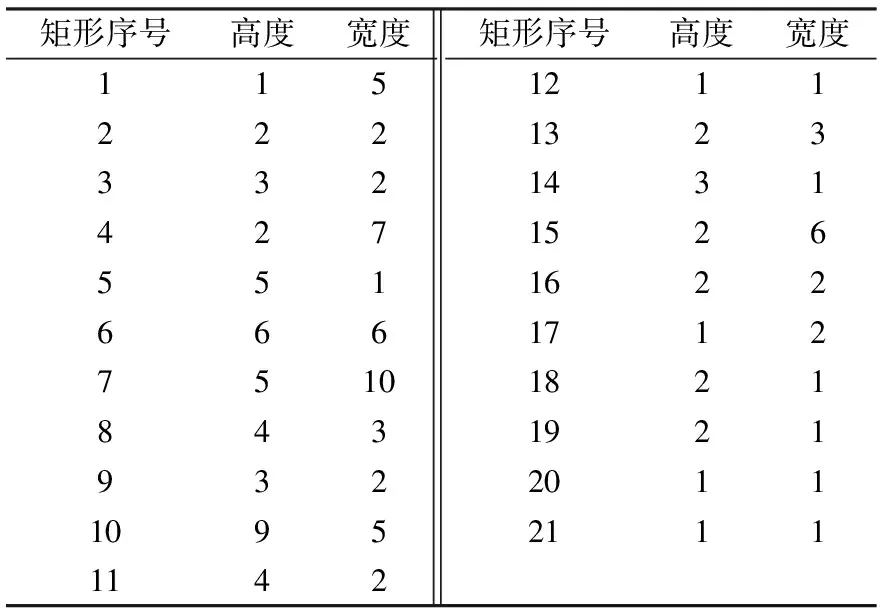
为了检验所建模型的准确性和有效性，将两个模型分别应用于文献[13]中一个中等规模的标杆算例Ex5，采用GAMS/CPLEX软件进行求解，并将所得结果与文献[13]所建模型的求解结果进行比较。标杆算例Ex5所含矩形个数为21，条带箱列数为10，各矩形的高度和宽度见表1。

表1 标杆算例中各矩形的高度和宽度

Table 1 Height and width of each rectangle in the example

矩形序号高度宽度115222332427551666751084393210951142矩形序号高度宽度1211132314311526162217121821192120112111

标杆算例求解结果见表2，由模型(Ⅰ)和模型(Ⅱ)的计算结果得到的矩形铺设方案见图3。

表2 标杆算例的计算结果

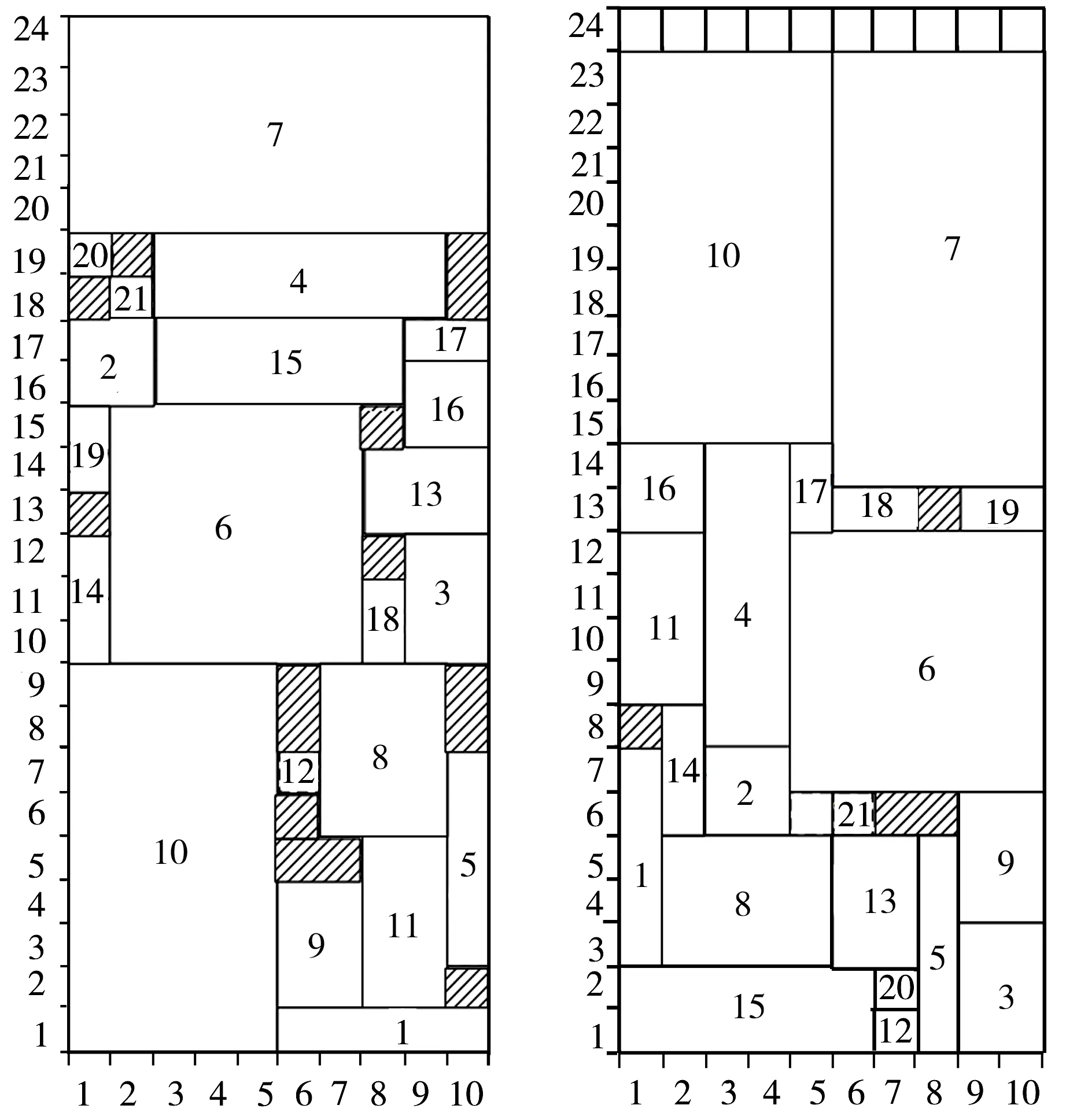
(a)模型(Ⅰ)(不旋转) (b)模型(Ⅱ)(可旋转)

图3 模型(Ⅰ)和模型(Ⅱ)求解标杆算例的最优布局方案

Fig.3 Optimal layout schemes of benchmark example solved by Model(Ⅰ) and Model(Ⅱ)

由表2和图3可见，所建离散化不旋转和可旋转的左下角定位模型均可有效求解出标杆算例的最优解；可旋转情形下的最优解要优于不旋转情形下的最优解(包含文献[13]模型和本文模型(Ⅰ)的计算结果)。

5 结语

本文针对离散化二维矩形条带装箱问题，利用各矩形的左下角单元坐标对矩形在条带箱中的放置位置进行定位，就不旋转和可旋转两种情形分别建立了该问题的纯整数线性规划模型。对标杆算例的求解结果验证了两个模型的有效性和准确性。

然而，所建两个模型只能求解出部分中小规模问题的最优解，对于大规模问题还应进一步研究启发式或元启发式求解算法。

[1] Hifi M. Exact algorithms for the guillotine strip cutting/packing problem[J]. Computers and Operations Research, 1998, 25(11): 925-940.

[2] Burke E K, Kendall G, Whitwell G. A new placement heuristic for the orthogonal stock-cutting problem[J]. Operations Research, 2004, 52(4):655-671.

[3] Chen Mao, Huang Wenqi. A two-level search algorithm for 2D rectangular packing problem[J]. Computers and Industrial Engineering, 2007, 53(1):123-136.

[4] Cui Yaodong, Yang Yuli, Cheng Xian, et al. A recursive branch-and-bound algorithm for the rectangular guillotine strip packing problem[J]. Computers and Operations Research, 2008, 35(4): 1281-1291.

[5] 张德富,韩水华,叶卫国. 求解矩形Packing问题的砌墙式启发式算法[J]. 计算机学报, 2008, 31(3)：509-515.

[6] 蒋兴波,吕肖庆,刘成城.二维矩形条带装箱问题的底部左齐择优匹配算法[J]. 软件学报, 2009, 20(6)：1528-1538.

[7] Leung S C H, Zhang Defu. A fast layer-based heuristic for non-guillotine strip packing[J]. Expert Systems with Applications, 2011,38(10): 13032-13042.

[8] 彭碧涛，周永务. 求解2D条带矩形Packing问题的迭代启发式算法[J]. 软件学报, 2012, 23(10)：2600-2610.

[9] 黄岚，齐季，谭颖，等. 一种求解矩形排样问题的遗传-离散粒子群优化算法[J]. 电子学报, 2012, 40(6)：1103-1107.

[10]Chen Bili, Wang Yong, Yang Shuangyuan. A hybrid demon algorithm for the two-dimensional orthogonal strip packing problem[J]. Mathematical Problems in Engineering,2015(3):1-14.

[11]Yang Shuangyuan, Han Shuihua, Ye Weiguo. A simple randomized algorithm for two-dimensional strip packing[J]. Computers and Operations Research, 2013, 40(1):1-8.

[12]于洪霞，张绍武，张立卫. 二维装箱问题非线性规划模型和算法[J]. 大连理工大学学报, 2008, 48(2)：308-312.

[13]Castro P M, Oliveira J F. Scheduling inspired models for two-dimensional packing problems[J]. European Journal of Operational Research, 2011, 215(1):45-56.

[责任编辑 尚 晶]

Discrete-space locating model with left bottom corner coordinate for 2D rectangular strip packing problem

LiMing1,ZhangManman1,QiXiaoying1,TangQiuhua2

(1.College of Science, Wuhan University of Science and Technology, Wuhan 430065, China;2. College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China)

To solve the discrete 2D rectangular strip packing problem (2DR-SPP) with non-rotating rectangles and rotatable ones respectively, two integer linear programming models are established which locate every rectangle according to its left bottom corner coordinate. The proposed models are employed to solve a benchmark example by GAMS/CPLEX software and the results demonstrate their effectiveness and accuracy.

two-dimensional packing problem; discretization; location model; integer programming

2016-08-28

湖北省教育厅科学技术研究项目(D20161104).

李 明(1976-)，男，武汉科技大学副教授，博士. E-mail:lmzqx@163.com

TP18;TP301

A

1674-3644(2016)06-0468-04