有限状态多期模型下的最小κ熵等价鞅测度期权定价
2016-06-09翟迎新让光林
翟迎新,让光林
(武汉大学数学与统计学院,湖北 武汉,430072)
有限状态多期模型下的最小κ熵等价鞅测度期权定价
翟迎新,让光林
(武汉大学数学与统计学院,湖北 武汉,430072)
本文用一个纯跳的随机过程来描述标的资产价格的动态性,称为有限状态多期模型。考虑只有一个标的资产的期权定价模型,给出其最小κ熵等价鞅测度,在此基础上采用Monte Carlo模拟欧式期权定价MCMEM(κ)方法,分别以虚拟Black-Scholes世界中欧式期权价格和现实金融市场中的麦当劳股票期权价格为例,对MCMEM(κ)和Black-Scholes公式等其他定价方法进行比较,验证了MCMEM(κ)的可行性。
最小熵;等价鞅测度;期权定价;有限状态多期模型;欧式期权
Black-Scholes期权定价公式为包括股票、债券、货币、商品在内的新兴衍生金融市场中各种根据市价变动定价的衍生金融工具的合理定价奠定了基础。但Black-Scholes期权定价模型中有很多假设与现实市场不符,如股票价格行为服从对数正态分布模式、在期权有效期内无风险利率和金融资产收益恒定等。随着金融理论的不断完善,很多研究人员开始探讨放松Black-Scholes模型中的某些条件以获得新的期权定价模型。例如,用随机变量替代Black-Scholes期权定价模型中的某些固定参数,得到随机波动率模型[1];在标的资产价格运动模型中引入跳-扩散过程或纯跳过程[2];用非参数方法对衍生产品进行定价,如正则定价法[3-4]。
本文拟采用一个纯跳的随机过程来描述标的资产价格,考虑只有一个标的资产的有限状态多期模型,给出其最小κ熵等价鞅测度,并提出基于Monte Carlo模拟的欧式期权定价方法,然后分别以虚拟Black-Scholes世界中欧式期权和现实市场中的麦当劳股票期权价格为例,对最小κ熵等价鞅测度定价方法(MCMEM(κ))和Black-Scholes公式等其他定价方法进行比较,以验证MCMEM(κ)的可行性。
1 最小κ熵等价鞅测度定价方法
1.1 有限状态多期模型
本文采用文献[5]建议的逐天记录价格变化的模型作为股票价格运动模型。记当前时刻的股票价格为S0,T天以后的股票价格可以表示成
(1)
式中:Zj是从第j-1天到第j天股票价格的变化量,即Zj=Sj-Sj-1。
假定所有价格变化来自一个有限状态空间Z={z1,z2,…,zn},其中n是状态的个数。关于股票价格逐日的变化量,作如下假定(APC):
(1)Z中元素的个数是有限的, 可以由历史数据估计出来;
(2)标的资产价格的逐日变化之间相互独立;

将以上模型称为有限状态多期模型。这个模型中每天股票价格的可能变化超过2个,一般而言这样的市场都是不完备市场。
在不完备市场下,等价鞅测度集合通常不是单点集合,需要从许多等价鞅测度中选取一个合适的定价测度。备选原则有多种,应用相对熵最小原则就可以得到最小κ熵等价鞅测度[6],该测度诱导出来的定价泛函是一个正的泛函,从而是一个合适的定价测度。
1.2 最小κ熵等价鞅测度
记市场价格变化的自然测度为P,记它的等价鞅测度为Q。由无套利定价原理可知, 对于一个T天的价格过程, 等价鞅测度Q必须满足:


(2)

在有限状态多期模型中, 第j天价格变化的自然测度为
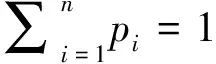
P的等价鞅测度Q必须满足式(2)和下面的约束:
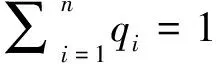
定义1 设(Ω,F,Ρ)为一个概率空间,Q为可测空间(Ω,F)上的另一概率测度,定义测度Q相对于测度P的相对κ熵[6]为
Hκ(Q|
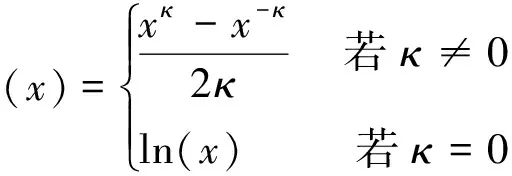
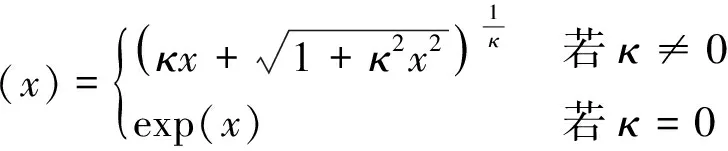
对于有限状态多期模型而言,Q关于P的相对κ熵为

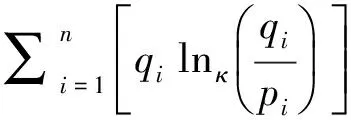
下面研究一种最简单的情形: 假定所考虑的期权写在一种标的资产上,在T天以后到期,标的资产在所考虑时间段内没有红利支付,在到期日前银行利率是一个常数,没有交易费用,这正是文献[3]中考虑的情形。
由式(2)以及关于股票价格变化的假设(APC),有
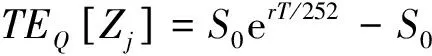
可以改写为
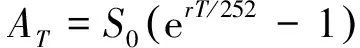
根据最小κ熵等价鞅测度的定义,有如下凸优化问题:

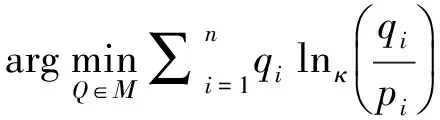

使用拉格朗日乘数法,取两个拉格朗日乘子分别为λ和γ,则目标函数为
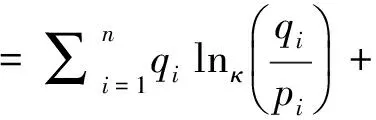
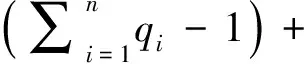
(3)
式中:Q=(q1,q2,…,qn)。
分别对目标函数式(3)关于Q、λ、γ求偏导后可得到以下方程组:
λ+γzi=0,i=1,2,…,n
(4)
(5)
(6)

=1,则
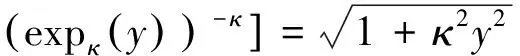
由式(4)可以得到

(7)
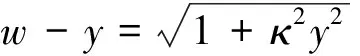
(8)

{[-(λ+γzi)-

i=1,2,…,n
(9)
其中,(λ,γ)∈R2为以下方程组的唯一解:
从命题1可以看出, 最小κ熵等价鞅测度是关于S0、r、T、Ρ的函数。用LINGO软件可直接求得Q*,然后就能够根据无套利定价原理给出T天后到期、敲定价格为K的欧式期权的风险中性价格:
(10)
1.3 Monte Carlo模拟计算风险中性价格
对于一个T天后到期的欧式看涨期权,标的资产的价格轨道中有T个价格变化需要模拟。这些价格变化被认为是从一个有限状态集合中按照最小κ熵等价鞅测度Q*独立抽取的样本, 按如下方式记向量QC:QC(1)=0,QC(i)=QC(i-1)+Q*(i-1),i=2,3,…,n。
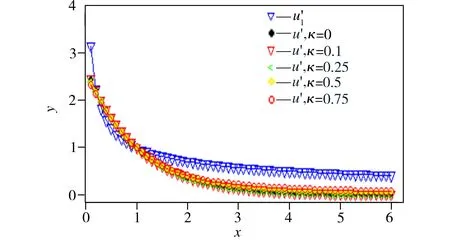
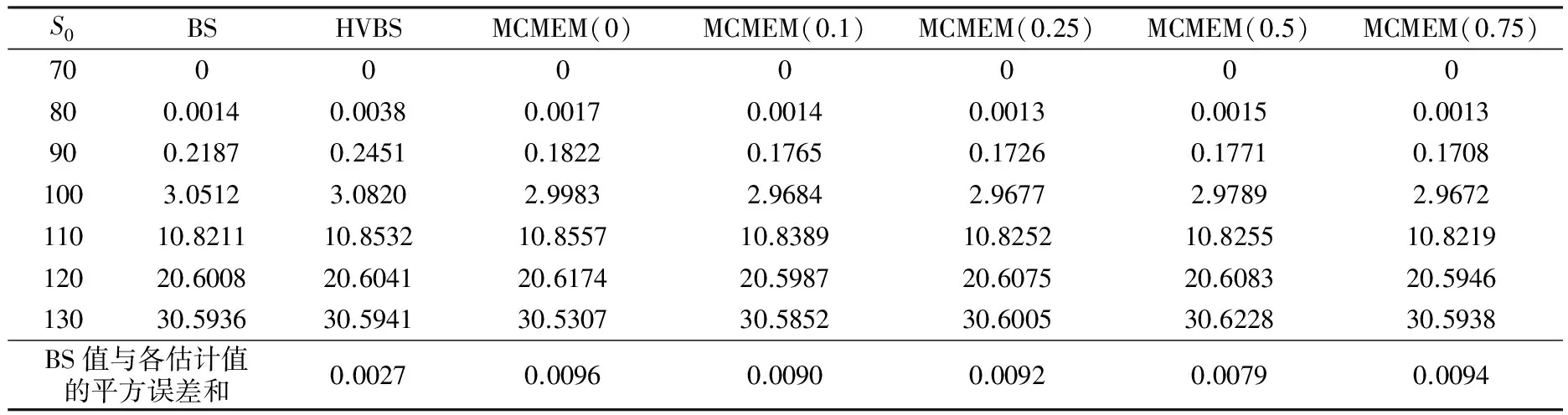
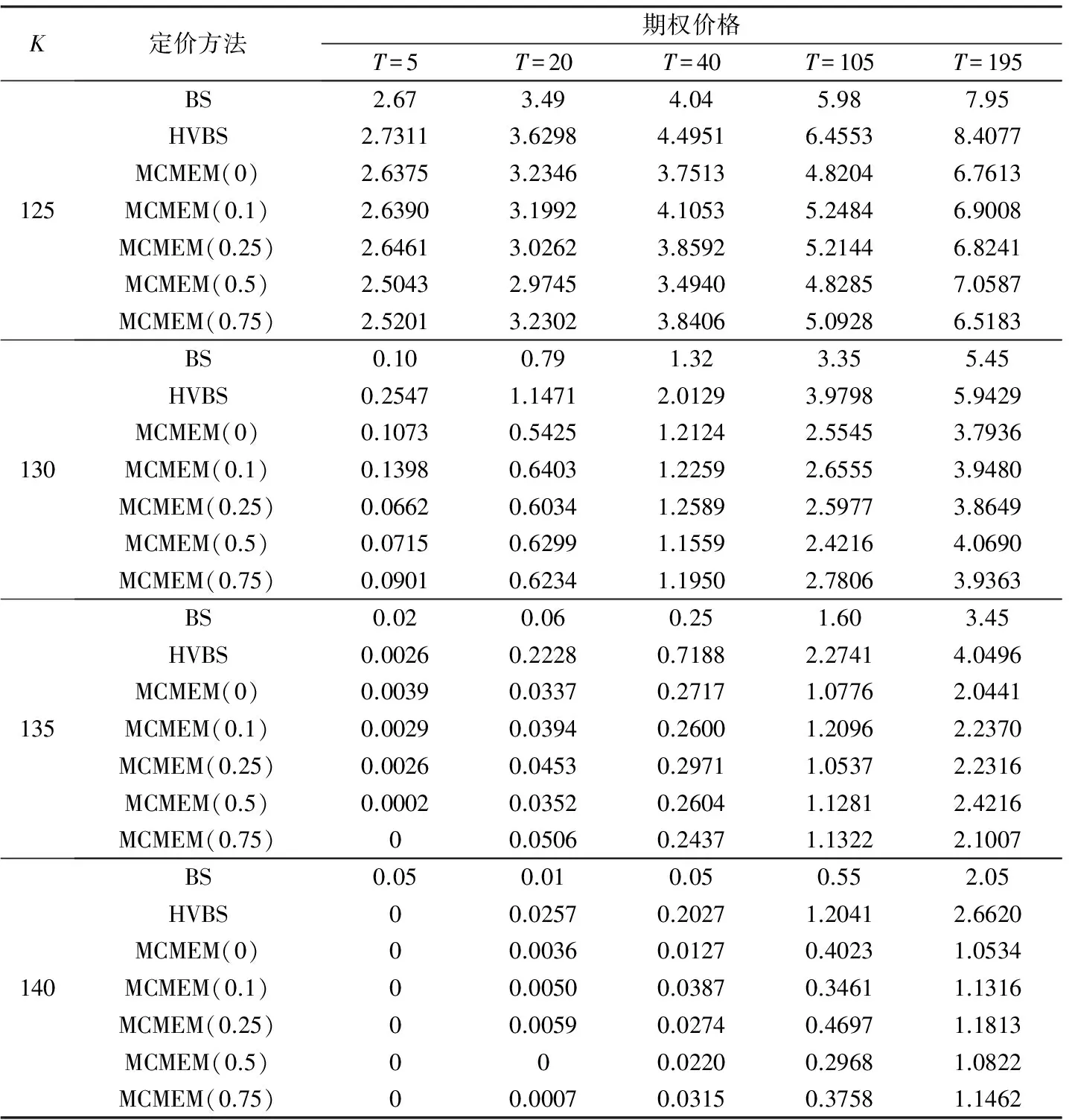
为了模拟出一条轨道上的第j次价格变化Zj,首先随机抽取一个区间 [0,1] 上的均匀分布随机变量s,如果满足QC(i)≤s (1)空气滤清器阻塞清洗空气滤清器芯子或清除指质滤芯上的灰尘,必要时应更换,以及检查机油平面是否正常。(2)排气管阻塞或接管过长,转弯半径太小、弯头过多清除排气管内积碳,重新排气接管,弯头不能多余三个,并有足够大的排气截面。 其中,Zk,j为第k条价格轨道中j时刻的价格变动。 在下面的研究中, 每次估计期权价格都用 Monte Carlo 方法[7]产生N=1000条价格的样本轨道,然后把样本平均作为期权价格的估计值。本文将采用Monte Carlo模拟方法计算风险中性价格的最小κ熵等价鞅测度定价方法记为MCMEM(κ),而将最小熵等价鞅测度定价方法[7]记为MCMEM(0)。 图1 效用函数曲线的对比 表1 不同κ值所对应的u′与的偏差 以上分析说明,最小κ熵等价鞅测度更加贴近实际的金融市场,所以MCMEM(κ)定价方法理论上要优于MCMEM(0)定价方法。 在虚拟Black-Scholes世界中,本文采用如下改进的方法对欧式期权价格进行估计:生成一条长度为T的价格轨道, 然后从这些价格中估计出历史波动率δ和市场状态集合Z,计算出相应的基于历史波动率的Black-Scholes值(HVBS)和MCMEM(κ)值,并与真实的Black-Scholes值(BS)进行比较。由于价格轨道产生的随机性,实验重复以上过程100次,取其平均值作为各种方法对欧式期权价格的估计。 在上述随机模型中,设连续复利r=0.05,几何布朗运动的漂移和波动率分别为μ=0.05,δ=0.2。计算出固定敲定价格K=100、到期日T=30、当前市场价格S0不同时的期权价格,结果如表2所示。 表2 采用不同方法的期权定价(K=100,T=30) 由表2可见,HVBS值与BS值的平方误差和最小,而相比于MCMEM(0),MCMEM(κ)(κ=0.1,0.25,0.5,0.75)值与BS值的平方误差和较小,这也进一步说明MCMEM(κ)方法比MCMEM(0)方法在期权定价中的表现更好。HVBS值与BS值的平方误差和很小是因为HVBS在估计期权价格的过程中用到了标的资产价格运动是几何布朗运动的信息,而MCMEM(κ)方法却可以在没有利用任何有关标的资产价格运动过程分布特性的前提下得到如此准确的估计,说明其能够有效地从标的资产的历史价格数据中收集可用于期权定价的信息。因此,MCMEM(κ)方法是可行的且优于最小熵等价鞅测度定价方法 。 一种期权定价方法在虚拟世界中表现得再好, 也不能保证它在现实市场中的适用性,所以下面以麦当劳股票为例分析MCMEM(κ)方法在实际金融市场中的表现。 以麦当劳股票(股票代码MCD)为标的资产,选取其在2012年1月9日至2016年4月25日期间的1080个收盘价数据,初始值S0取股票历史价格的最后一个值,即2016年4月25日的收盘价,故S0=127.46。取无风险利率为1%,分别对到期日T=5、20、40、105、195,执行价格K=115、120、125、130、135、140的期权价格进行分析。 采用R语言编程计算,由麦当劳股票的1080个收盘价数据和其他给定的参数,得到欧式看涨期权的HVBS值和MCMEM(κ)值 (κ=0,0.1,0.25,0.5,0.75),结果见表3。表4为麦当劳股票真实期权价格与各定价方法下估计值的平方误差和。 由表3可见,MCMEM(κ)定价的拟合效果比较好,更加验证了该方法的适用性和可行性。MCMEM(κ)方法估计的期权价格在到期日较短时优于基于历史波动率的Black-Scholes方法所得期权价格(HVBS),但是在到期日较长时,MCMEM(κ)定价法得到的期权价格偏离真实价格较远,这是因为历史价格的数据有限,短期变化可以从历史信息中表现出来,但是长期的变化则无法根据有限的历史信息完全预测。 表3 采用不同方法的麦当劳股票期权定价 续表 K定价方法期权价格T=5T=20T=40T=105T=195125BS2.673.494.045.987.95HVBS2.73113.62984.49516.45538.4077MCMEM(0)2.63753.23463.75134.82046.7613MCMEM(0.1)2.63903.19924.10535.24846.9008MCMEM(0.25)2.64613.02623.85925.21446.8241MCMEM(0.5)2.50432.97453.49404.82857.0587MCMEM(0.75)2.52013.23023.84065.09286.5183130BS0.100.791.323.355.45HVBS0.25471.14712.01293.97985.9429MCMEM(0)0.10730.54251.21242.55453.7936MCMEM(0.1)0.13980.64031.22592.65553.9480MCMEM(0.25)0.06620.60341.25892.59773.8649MCMEM(0.5)0.07150.62991.15592.42164.0690MCMEM(0.75)0.09010.62341.19502.78063.9363135BS0.020.060.251.603.45HVBS0.00260.22280.71882.27414.0496MCMEM(0)0.00390.03370.27171.07762.0441MCMEM(0.1)0.00290.03940.26001.20962.2370MCMEM(0.25)0.00260.04530.29711.05372.2316MCMEM(0.5)0.00020.03520.26041.12812.4216MCMEM(0.75)00.05060.24371.13222.1007140BS0.050.010.050.552.05HVBS00.02570.20271.20412.6620MCMEM(0)00.00360.01270.40231.0534MCMEM(0.1)00.00500.03870.34611.1316MCMEM(0.25)00.00590.02740.46971.1813MCMEM(0.5)000.02200.29681.0822MCMEM(0.75)00.00070.03150.37581.1462 表4 麦当劳股票真实期权价格与各定价方法所得估计值的平方误差和 从表4可以看出真实期权价格与MCMEM(κ)(κ=0.1,0.25,0.5,0.75)的平方误差和要小于其与MCMEM(0)的平方误差和,这为MCMEM(κ)定价方法的存在必要性进一步提供了依据。 本文引入了一种新的期权定价方法——采用Monte Carlo模拟的最小κ熵等价鞅测度定价MCMEM(κ),它是一种完全由数据驱动的定价方法,不依赖任何关于股票价格分布的假设,也可以嵌入随机红利或随机利率的影响,因此应用比较灵活。 从虚拟Black-Scholes世界中欧式期权定价随机模拟实验结果和现实金融市场中麦当劳股票期权定价结果来看,MCMEM(κ)方法是可行的,且在一定程度上要优于MCMEM(0)。 [1] Hull J, White A. The pricing of options on assets with stochastic volatilities[J].The Journal of Finance, 1987,42:281-300. [2] Merton R C. Option pricing when underlying stock returns are discontinuous[J].Journal of Financial Economics,1976,3:125-144. [3] Stutzer M.A simple nonparametric approach to derivative security valuation[J].Journal of Finance,1996,51:1633-1652. [4] 唐月涵.任意期权的正则定价[D].南京:南京理工大学,2014. [5] Rydberg T H, Shephard N.A modeling framework for the prices and times of trades made on the New York Stock Exchange[EB/OL]. Nuffield College Working Paper W99-14.(1999-06-04)[2016-04-05].https://ssrn.com/abstract=164170. [6] Trivellato B.The minimal κ-entropy martingale measure[J].International Journal of Theoretical and Applied Finance,2012,15(5):1250038. [7] 黄光辉.有限状态多期模型下的期权定价和市场风险研究[D].武汉:华中科技大学,2006. [8] 汤思英,刘继春,杜立金.最小对称熵鞅测度和不完备市场中的定价问题[J].厦门大学学报:自然科学版,2004,43(4):465-468. [责任编辑 尚 晶] Option pricing based on the minimalκ-entropy equivalent martingale measure for finite state multi-period model ZhaiYingxin,RangGuanglin (School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China) This paper uses a pure jump stochastic process called the finite state multi-period model to describe the dynamics of underlying asset prices. Option pricing model for only one underlying asset is considered and the minimumκ-entropy equivalent martingale measure is deduced. On this basis, a pricing method for European option using Monte Carlo simulation named as MCMEM(κ) is proposed. MCMEM(κ) and other pricing methods such as Black-Scholes formula are used to evaluate European option price in a virtual Black-Scholes world and the option price of McDonald’s stock in the real financial market. The comparison results verify the feasibility of MCMEM(κ). minimal entropy; equivalent martingale measure; option pricing; finite state multi-period model; European option 2016-07-06 国家自然科学基金资助项目(11571272). 翟迎新(1992-),女,武汉大学硕士生.E-mail:2014202010053@whu.edu.cn 让光林(1970-),男,武汉大学副教授,博士.E-mail:glrang.math@whu.edu.cn F830.9;F224 A 1674-3644(2016)06-0472-06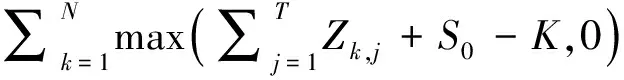
2 MCMEM(κ)与MCMEM(0)的比较

3 MCMEM(κ)在虚拟Black-Scholes世界中的应用
4 MCMEM(κ)在现实金融市场中的应用


5 结语
