一种适用于任意高阶间断有限元的高精度非分裂完全匹配层吸收边界方法*

何洋洋 翁 斌 张金淼

(1.中海油研究总院 北京 100028； 2.中国石油大学(北京) 北京 102249)

一种适用于任意高阶间断有限元的高精度非分裂完全匹配层吸收边界方法*

何洋洋1,2翁 斌1张金淼1

(1.中海油研究总院 北京 100028； 2.中国石油大学(北京) 北京 102249)

任意高阶间断有限元法常用的吸收边界条件存在对切向入射波吸收效果不佳等问题。本文提出了一种适用于任意高阶间断有限元的高精度非分裂完全匹配层吸收边界方法，将非分裂完全匹配层吸收边界应用于任意高阶间断有限元地震波数值模拟方法中，建立了完全匹配层内新的波动方程，推导了其求解过程及在三角形单元内的表达形式，最后给出了离散化格式。该方法在完全匹配层也可以求得任意高阶时间精度和空间精度的数值解，与计算区域的精度一致，减少了边界反射波的能量。数值算例模拟结果表明，本文方法对不同角度的入射波具有较好的吸收效果，适用于高泊松比介质。

非分裂完全匹配层；任意高阶间断有限元；高精度；不同角度入射波；高泊松比

地震波场数值模拟是勘探地球物理的重要研究手段，实际应用中，可以通过求解弹性波动方程来实现[1-2]。针对具有复杂几何结构介质中的地震波传播进行高精度模拟是一项具有挑战性的工作，近年来已提出许多新的方法，比如有限体积法[3]、混合有限元法[4]、边界元法[5]等。Käser和Dumbser[6-7]提出了弹性介质中的任意高阶间断有限元地震波数值模拟方法，该方法将间断有限元法[8]和任意高阶时间积分法[9]相结合，从而得到空间和时间上任意高阶精度的数值解，能够很好地处理具有局部小尺度结构的复杂介质模型，应用范围广泛。实际应用中，由于地震波数值模拟每次只能计算有限区域中的波传播，所以必须在计算区域的人工边界处使用吸收边界才能模拟无限大的地下介质。Käser和Dumbser[6]给出了一种简单的吸收边界，可以很好地吸收法向方向入射波，是任意高阶间断有限元法常用的吸收边界处理方法，但在某些情况下，比如切向入射波，或者模型的角点处，这种吸收边界不能有效地对入射波进行吸收。

Bérenger[10]在电磁波场模拟中提出了完全匹配层吸收边界条件(PML)，这是目前已知的效果最好的吸收边界条件。Chew和Liu[11]以及Hastings等[12]将完全匹配层用于弹性波模拟，取得了好的吸收效果。目前完全匹配层普遍使用波场分裂的方法，以避免计算中出现时间域卷积，但是当地震波切向入射时该方法的边界反射系数会变大，产生强能量的反射波，对波场模拟结果造成干扰。

Komatitsch和Martin[13]，Drossaert和Giannopoulos[14]等分别提出了一种非分裂形式的完全匹配层算法(CPML)，采用递归卷积技术[15]，在提高吸收效果的同时并没有增加运算量。该方法在完全匹配层内添加了一个滤波器，地震波切向入射时会在匹配层内传播很长的距离，滤波器会对这种波产生强的吸收衰减，吸收效果优于传统的完全匹配层算法。

本文将非分裂完全匹配层吸收边界应用于任意高阶间断有限元地震波数值模拟方法中，建立了完全匹配层内新的波动方程，推导了其求解过程及在三角形单元内的表达形式，最后给出了离散化格式。通过数值算例分析，研究了该算法对不同角度入射波的吸收效果以及该算法在高泊松比介质中波场模拟的适用性。

1 高精度非分裂完全匹配层算法

1.1 完全匹配层内波动方程的建立

二维各向同性弹性介质中的波动方程为

(1)

(2)

(3)

式(1)～(3)使用张量表示法。其中，u=(σxx,σzz,σxz,v,w)T为5个未知量组成的向量，up、uq分别为向量中的第p、q个分量，p=1，…，5，q=1，…，5为自由指标；时间t∈R，x=(x,z)T∈R2；σxx=σxx(x,t)、σzz=σzz(x,t)是法向应力分量，σxz=σxz(x,t)是切向应力分量；v=v(x,t)和w=w(x,t)是质点速度x方向和z方向分量。Apq=Apq(x)和Bpq=Bpq(x)是大小为5×5的Jacobian矩阵，λ=λ(x)和μ=μ(x)是拉梅常数，ρ=ρ(x)为密度。Sp(x,t)=(S1(x,t),S2(x,t),S3(x,t),S4(x,t),S5(x,t))T是震源向量。

在时间域内，非分裂完全匹配层内的波动方程可以表示为[13-14]

(4)

(5)

(6)

(7)

式(4)～(7)中：dj(x)为衰减系数；aj(x)和κj(x)用来控制能量衰减的速度，地震波模拟中可取κx(x)=κz(x)=1[14]。H(t)为阶跃函数。L为完全匹配层的厚度，可选为1/3或1/2波长，当吸收效果不能满足要求时，则适当增加完全匹配层的厚度。衰减系数在完全匹配层的每个三角形单元内是随空间位置而变化的。对于一般情况下的波场正演，可令dmax=-3vPlgRc/(2L),αmax=πf0，其中vP是介质的纵波速度，f0是震源子波的主频，Rc为数值离散后的反射系数，通常取0.1%[13-14]。

本文对式(4)进行改写，得到

(8)

(9)

式(9)中：S1、S2、S3、S4、S5是式(1)中的震源项，因为完全匹配层内没有震源，所以此处S1=S2=S3=S4=S5=0。

1.2 完全匹配层内波动方程的求解

(10)

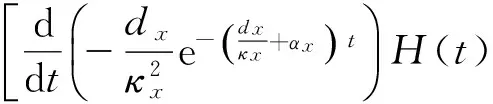
(11)

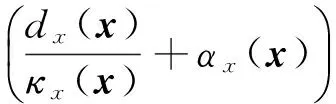
(12)

(13)

对于计算区域，Käser和Dumbser[6]在使用任意高阶间断有限元法求解式(1)而得到up的k阶时间导数时使用了式(14)，即

-1)k(Ap q+Bp q)kuq(x,t)+

(14)

式(14)中，Sq表示震源向量中的第q个分量，其k阶时间导数可以由震源的时间域表达式直接计算得到。在求解t时刻方程时，可先求得uq的数值解，然后通过式(14)求得up的第k阶时间导数，从而可以得到k阶精度的数值解。

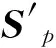
图1 完全匹配层内up第k阶时间导数的计算步骤

1.3 三角形单元内的数值解

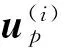
(15)

(16)

式(15)～(16)使用张量表示法。其中，l=1，…，N，为自由指标；N为多项式基函数的个数，取决于多项式基函数的阶数；Φl(x)的阶数决定了任意高阶间断有限元法的计算精度，阶数越高，精度越高。

1.4 离散化

对于式(13)和式(14)，两边同时乘以试验函数Φn(x)，并在x-z坐标系下的三角形单元T(i)内进行积分，然后将积分式映射到ξ-η坐标系下的标准三角形单元TE中。考虑到多项式基函数为正交多项式，式(13)和式(14)在第n个时间步的离散计算格式分别为

]n=

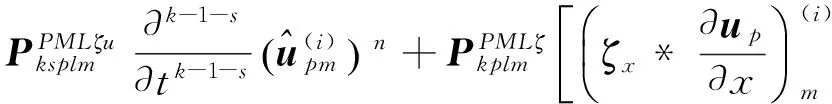
(17)

(18)

式(17)～(18)中：l=1,…，N，m=1，…，N，为不同的自由指标；〈·〉表示在标准三角形单元TE中的积分，积分项O、P都可以在TE中提前计算，这样可以减少正演模拟的计算量。

2 数值算例分析

2.1 均匀弹性介质

均匀弹性介质模型(图2)大小为600 m×600 m的正方形，介质中P波速度为2 500 m/s，S波速度为1 225 m/s，泊松比为0.34，密度为2 000 kg/m3。本模型所用震源有2种:第1种是胀缩源，只产生P波;第2种是剪切源，只产生S波。震源位于(150 m,150 m)处，震源子波为主频f0=20 Hz的Ricker子波，子波时延为t0=0.05 s。波场模拟总时长为T=0.75 s，时间步长为Δt=0.000 3 s。

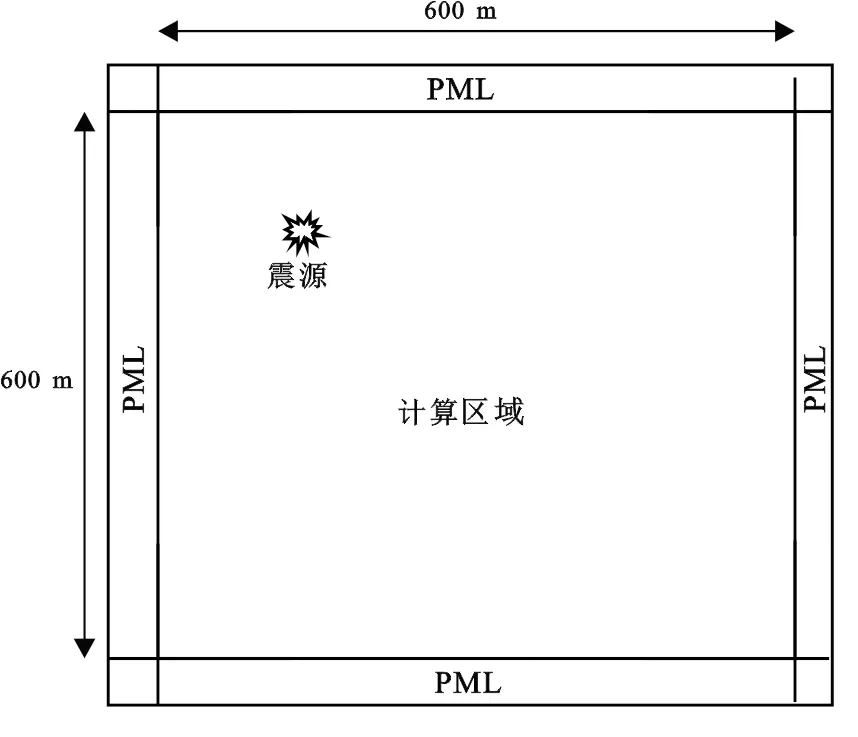
图2 均匀弹性介质模型

分别使用高精度非分裂完全匹配层算法及常用的吸收边界处理方法[6]对均匀弹性介质模型进行波场模拟，为了衡量吸收边界对入射波的吸收效果，再按照Drossaert和Giannopoulos的方法[14]计算波场的相对误差(误差越小，说明吸收边界的效果越好)，其结果见图3。可以看出，无论是P波还是S波，本文方法对不同角度入射波的吸收效果都优于常用方法，地震波在x=150 m处为法向入射，在x=600 m处为切向入射，此间吸收边界与震源的距离不断增大，而且随着距离的增加，地震波的入射角变大，常用方法的吸收边界产生了较强能量的反射，而本文方法仍然可以有效吸收P波和S波。对于本文方法，可以得出如下认识：①对P波的吸收效果优于对S波的吸收效果，因为P波单位波长内所含的三角形单元个数多于S波单位波长内所含的三角形单元个数，精度相对较高；②使用4阶精度的吸收效果优于使用3阶精度的吸收效果；③完全匹配层越厚，边界吸收效果越好，但是相应的计算量也增加了。

图3 均匀弹性介质中波场模拟的相对误差

2.2 两层弹性介质

在高泊松比情况下，一些数值模拟方法有可能出现不稳定的现象，因此通过模拟高泊松比两层弹性介质中波的传播检验本文方法的有效性。两层弹性介质模型(图4)大小为1 000 m×700 m。第一层介质中，P波速度为1 500 m/s，S波速度为0.1 m/s，密度为1 000 kg/m3，泊松比接近0.5，只能传播P波。第二层介质中，P波速度为2 400 m/s，S波速度为1 100 m/s，密度为1 800 kg/m3。本模型所用震源为胀缩源，只产生P波，震源位于(200 m,200 m)处。波场模拟总时长为1 s，时间步长为Δt=0.000 1 s。

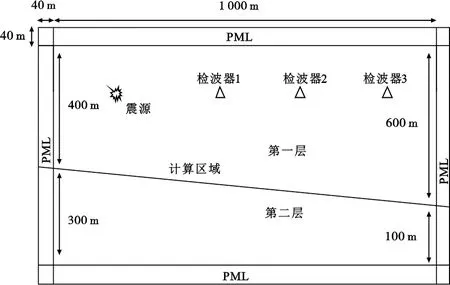
图4 两层弹性介质模型

分别使用3阶精度非分裂完全匹配层算法及常用的吸收边界处理方法[6]对两层弹性介质模型进行波场模拟,其结果见图5、6。从图5可以看出：常用方法对法向入射波具有非常好的吸收效果，垂直入射上边界的地震波能量完全被吸收，没有产生边界反射波；非垂直入射的地震波能量不能完全被吸收，产生了边界反射波，而且入射角越大，边界反射波的能量越强。由倾斜界面反射产生的上行P波在左边界产生了较强的边界反射波，由倾斜界面透射产生的下行P波和S波在左边界和下边界都产生了较强的边界反射波。而从图6可以看出：本文方法对不同角度入射地震波的吸收效果明显，不会产生强能量的反射波。

如果不考虑人工边界产生的反射波，检波器应该只接收到从两层介质间界面处反射回来的波，由于第一层介质的S波速度近似为0，只有P波能在第一层介质中传播，检波器只接收到一个P波波形才是正确的模拟结果。从图7可以看出：在常用方法计算结果中，3处检波器在P波前方和后方均接收到了不应存在的干扰波波形；而本文方法在高泊松比条件下仍然能够有效地吸收入射波，3处检波器均只接收到了一个P波波形，没有受到其他边界反射波产生的干扰。

图5 Käser和Dumbser方法[6]计算的两层弹性介质波场快照(质点速度z方向分量)

图6 高精度非分裂完全匹配层算法计算的的两层弹性介质波场快照(质点速度z方向分量)

图7 两层弹性介质中波场模拟检波器接收到的波形(质点速度z方向分量)

3 结论

本文提出了一种高精度非分裂完全匹配层算法，该算法将非分裂完全匹配层吸收边界用于任意高阶间断有限元地震波数值模拟中，使完全匹配层和计算区域解的精度一致，能够达到任意高阶的空间精度和时间精度。均匀弹性介质中波场数值模拟表明本文算法对不同角度的入射波具有较好的吸收效果，而两层弹性介质中波场数值模拟表明本文算法适用于高泊松比介质。

[1] 陈可洋.标量声波波动方程高阶交错网格有限差分法[J].中国海上油气,2009,21(4):232-236.

Chen Keyang.High-order staggered-grid finite difference scheme for scalar acoustic wave equation[J].China Offshore Oil and Gas,2009,21(4):232-236.

[2] 范廷恩,余连勇,杨飞龙,等.斜井VSP高斯射线束正演方法[J].中国海上油气，2014，26(5):30-35.

Fan Tingen,Yu Lianyong,Yang Feilong,et al.A method of Gaussian beam forward modeling in deviated-well VSP[J].China Offshore Oil and Gas,2014,26(5):30-35.

[3] DORMY E,TARANTOLA A.Numerical simulation of elastic wave propagation using a finite volume method[J].Journal of Geophysical Research:Solid Earth (1978—2012),1995,100(2):2123-2133.

[4] COHEN G,FAUQUEUX S.Mixed finite elements with mass-lumping for the transient wave equation[J].Journal of Computational Acoustics,2000,8(1):171-188.

[5] 李绪宣,于更新,符力耘,等.应用边界元模拟方法分析复杂海底地震散射特征[J].中国海上油气,2011,23(6):357-361.

Li Xuxuan,Yu Gengxin,Fu Liyun,et al.Analysing seismic scattering characteristics of complex seabed by using the boundary-element simulation method[J].China Offshore Oil and Gas,2011,23(6):357-361.

[8] YE Ruichao,DE HOOP M V.A 3D discontinuous Galerkin method for the propagation and scattering of acousto-elastic waves[C]∥2014 SEG Annual Meeting,2014:3329-3333.

[9] TORO E F,MILLINGTON R C,NEJAD L A M.Towards very high order Godunov schemes[M].Springer US,2001:907-940.

[10] BERENGER J P.A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of computational physics,1994,114(2):185-200.

[11] CHEW W C,LIU Q H.Perfectly matched layers for elastodynamics:a new absorbing boundary condition[J].Journal of Computational Acoustics,1996,4(4):341-359.

[12] HASTINGS F D,SCHNEIDER J B,BROSCHAT S L.Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation[J].The Journal of the Acoustical Society of America,1996,100(5):3061-3069.

[13] KOMATITSCH D,MARTIN R.An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J].Geophysics,2007,72(5):155 -167.

[14] DROSSAERT F H,GIANNOPOULOS A.Complex frequency shifted convolution PML for FDTD modeling of elastic waves[J].Wave Motion,2007,44(7):593-604.

[15] RODEN J A,GEDNEY S D.Convolutional PML (CPML):an efficient FDTD implementation of the CFS-PML for arbitrary media[J].Microwave and Optical Technology Letters,2000,27(5):334-338.

(编辑：冯 娜)

A new algorithm of high precision unsplit perfectly matched layer absorbing boundary for the arbitrary high-order discontinuous Galerkin finite element

He Yangyang1,2Weng Bin1Zhang Jinmiao1

(1.CNOOCResearchInstitute,Beijing100028,China; 2.ChinaUniversityofPetroleum,Beijing102249,China)

The common absorbing boundary condition used commonly for arbitrary high-order discontinuous Galerkin finite element method could not efficiently absorb wave energy of grazing incidence. A new algorithm of high precision unsplit perfectly matched layer absorbing boundary is proposed for the arbitrary high-order discontinuous Galerkin finite element method. The unsplit perfectly matched layer is applied to seismic wave modeling with arbitrary high-order discontinuous Galerkin method, the new equation of the wave propagation in perfectly matched layer and its solution in triangle element are derived, and the discrete scheme is given. This scheme can obtain arbitrary high-order solutions in both time and space in the unsplit perfect match layer with the same solutions in the computational region, thus reducing the energy of reflectivity from absorbing boundary. Simulation results indicate that the method shows better absorbing effect on incident waves with different angles, and it is suitable for the material with high Poisson’s ratio.

unsplit perfectly matched layer; arbitrary high-order discontinuous Galerkin finite element; high precision; incident waves with different angles; high Poisson’s ratio

何洋洋，男，1984年生，工程师，2013年毕业于西安交通大学信号与信息处理专业，获博士学位，主要从事地震波场正演数值模拟研究工作。地址：北京市朝阳区太阳宫南街6号院海油大厦B座(邮编：100028)。E-mail：heyy9@cnooc.com.cn。

1673-1506(2016)01-0041-07

10.11935/j.issn.1673-1506.2016.01.006

TE132.1+4；P631

A

2015-03-26 改回日期：2015-05-21

*“十二五”国家科技重大专项“近海大中型油气田地震勘探技术(编号：2011ZX05023-005)” 部分研究成果。

何洋洋,翁斌,张金淼.一种适用于任意高阶间断有限元的高精度非分裂完全匹配层吸收边界方法[J].中国海上油气，2016,28(1)：41-47.

He Yangyang,Weng Bin,Zhang Jinmiao.A new algorithm of high precision unsplit perfectly matched layer absorbing boundary for the arbitrary high-order discontinuous Galerkin finite element[J].China Offshore Oil and Gas,2016,28(1):41-47.