基于Contourlet系数相关性的地震噪声压制方法*

王建花 王守东 刘燕峰

(1.中海油研究总院 北京 100028； 2.海洋石油勘探国家工程实验室 北京 100028；3.中国石油大学(北京)油气资源与探测国家重点实验室 北京 102249)

基于Contourlet系数相关性的地震噪声压制方法*

王建花1,2王守东3刘燕峰3

(1.中海油研究总院 北京 100028； 2.海洋石油勘探国家工程实验室 北京 100028；3.中国石油大学(北京)油气资源与探测国家重点实验室 北京 102249)

地震信号Contourlet变换的稀疏表达中，变换域关联系数具有较强的相关性，据此提出了一种基于Contourlet邻域系数相关性的自适应阈值地震去噪方法。该方法对每一点系数计算其邻域均方根振幅，利用这一点的系数值及其邻域均方根振幅计算其邻域系数相关性，根据邻域系数相关性自适应地确定阈值。数值模拟和实际资料的处理结果验证了本文方法的有效性，该方法在压制噪声的同时能够较好地保护有效信号。

Contourlet变换；随机噪声；地震噪声压制；邻域系数相关性；自适应

地震资料中随机噪声的存在严重影响地震资料的成像质量和解释精度。前人提出了多种压制地震资料随机噪声的处理技术，如K-L变换去噪技术[1]、F-X域滤波去噪技术[2]，多项式拟合去噪技术[3]、奇异值分解去噪技术[4]等。20世纪80年代初小波变换的出现为信号处理、图像处理及其他非线性科学的研究带来了革命性的影响，发展了基于小波变换的噪声压制方法[5-10]。对于“点奇异”的一维信号，小波能达到“最优”的非线性逼近阶；而处理含“线奇异”的二维信号时，由于二维可分离小波是由一维小波的张量积构成，这样形成的二维小波变换虽然容易检测出位于边缘上的不连续点，但是却无法准确地表示边缘点之间的连续性，因此基于小波变换的随机噪声压制方法的去噪能力受到限制，对地震信号信噪比的提高有限。

Contourlet变换是在小波变换基础上发展起来的[11]，它是采用“长条形”的基来逼近奇异曲线，基的“长条形”支撑区间实际上是“方向性”的一种表现，具有优越的非线性逼近能力。目前，Contourlet分析如同小波分析方法一样在信号和图像处理的多个领域得到了广泛应用。彭才[12]和张恒磊[13]都利用Contourlet变换研究了地震噪声的压制方法，其基本思想是在Contourlet变换域对Contourlet变换系数采用阈值处理，再做反变换，从而实现地震数据的去噪，其去噪效果优于基于小波变换的去噪方法。由于Contourlet系数具有冗余性，如果充分考虑这一特点，可以进一步提高其去噪能力。因此，笔者根据Contourlet系数冗余性的特点，研究了基于Contourlet邻域系数相关性的地震噪声压制方法,所提出的基于邻域系数相关性的Contourlet自适应阈值去噪方法充分考虑了Contourlet域中当前系数与邻域系数的相关性，针对Contourlet变换域中各系数与其邻域系数的关系设立了可变的阈值，因而比常规Contourlet阈值去噪方法具有更好的去噪能力。

1 Contourlet变换的基本原理

对二维图像进行Contourlet变换由两步完成，首先进行多尺度变换，然后再进行局部方向变换[11]。Do[11]给出了一个双滤波带结构的Contourlet变换:首先利用拉普拉斯金字塔(LP)分解来完成信号的多尺度分解并捕捉奇异点，然后利用方向滤波器组(DFB)将奇异点连成线性结构，这样就能够将图像展开成一系列轮廓线的和的形式。在频率域中，Contourlet变换可以实现多尺度、多方向的分解。

1.1 拉普拉斯金字塔分解

在某一尺度上，拉普拉斯金字塔分解是将图像分解为两部分：一部分为对原始图像做低通滤波后进行下采样的数据；另一部分是原始图像与预测数据的差值。假设信号用向量X来表示，低通滤波器和合成滤波器分别用H和G表示，上采样和下采样分别用矩阵U和D表示，则信号X的分解过程可以用下式表示：

A=D(H*X)

(1)

B=X-G*(UA)

(2)

这里*代表褶积运算，A和B分别是原始信号的低频子带信号和高频子带信号。LP分解的过程可以描述为：

1) 首先将原始信号通过低通滤波和下采样操作产生此信号的近似分量，也就是原始信号的低频子带信号；

2) 对此低频子带信号进行上采样和合成滤波，生成原始信号的预测信号；

3) 将原始信号与预测信号相减，即得到原始信号的高频子带信号。

利用每一级分解所产生的低频子带信号，LP分解可以迭代进行下去，生成一个低频信号和一系列的高频子带信号。LP分解可以实现对信号从精细尺度到粗略尺度的逼近，利用分解后的数据可以重构原来的图像，其重构过程是分解过程的逆过程。在某一尺度上重构时，首先将低频子带信号进行上采样和合成滤波，得到原始信号的预测信号，将预测信号与高频子带信号求和就得到了合成数据。

1.2 方向滤波器组

方向滤波器组可以把图像在频率域分解为多个子带，一般按2的幂次来分解，如果进行l级分解，就把图像在频率域分解为2l个子带。Do[11]给出了一种非常有效的方向滤波器组，该方法通过2个基本操作的组合实现方向滤波。第1个基本操作是一个双通道五点梅花滤波器组，该滤波器组可以将图像的二维谱分解为水平方向和垂直方向。五点梅花滤波器的采样矩阵是

(3)

第2个基本操作是一个剪切运算，相当于对图像的样点进行重新排序,对应的采样矩阵为

(4)

经过五点梅花滤波器组处理后，在水平分量中，与水平方向的夹角小于45°的同相轴得到加强；在垂直分量中，与垂直方向的夹角小于45°的同相轴得到加强。而剪切运算相当于将图像进行了倾斜。将五点梅花滤波器组和剪切运算进行各种组合，可以实现图像的方向滤波，将图像在频率域分解为多个子带。

1.3 Contourlet变换

(5)

图2a为一个二维原始图像数据，图2b是Contourlet分解后重构的图像，二者完全一致；在重构的数据减去原始数据后的图上(图2c)只能看到原图的一些影子，这说明利用分解后的系数可以完全地重构原来的图像。

图1 Contourlet变换频率域分解示意图

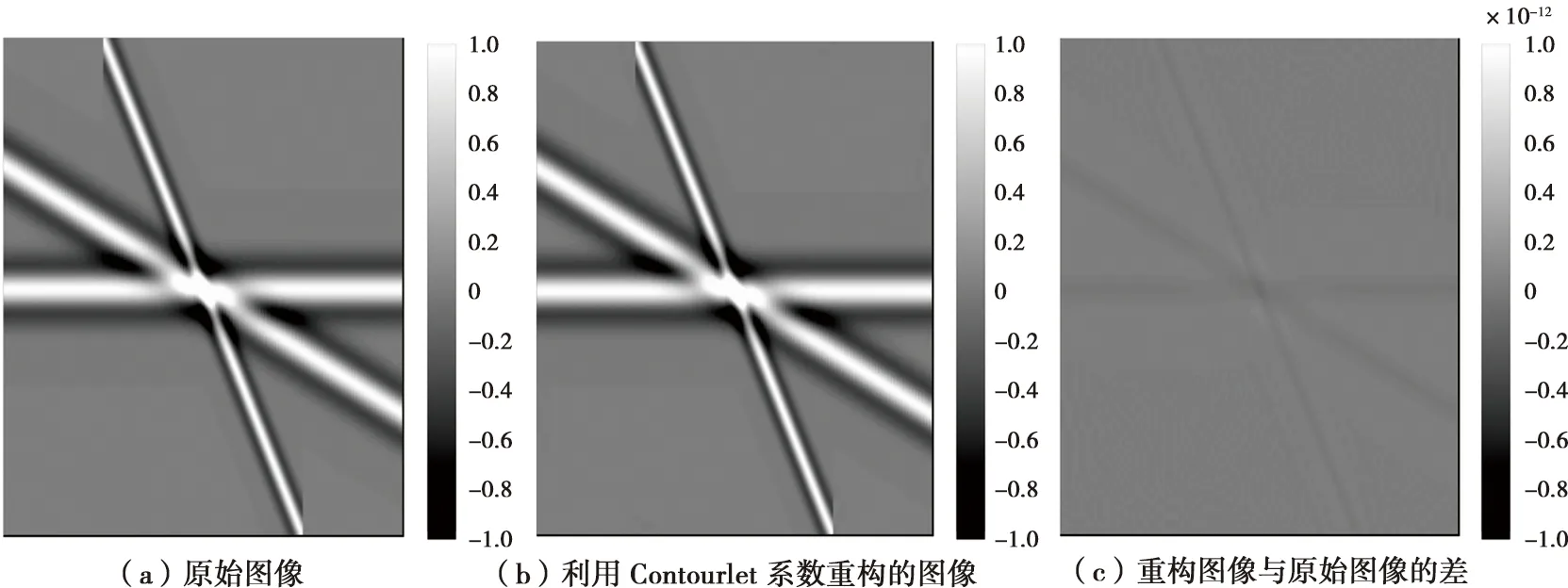
图2 Contourlet分解重构示意图

2 基于Contourlet邻域系数相关性的去噪方法

Contourlet变换可以实现对信号的稀疏表达，而且信号经Contourlet变换后，变换域系数是相互关联的而非完全独立，即如果当前Contourlet系数较大，其邻域系数可能也较大。基于这一思路，提出了一种基于邻域系数相关性的Contourlet自适应阈值去噪方法。该方法将地震资料看成是一个二维图像，依据它具有丰富纹理性的特点，压制地震记录中的随机噪声。

假设地震数据为F，通过Contourlet变换可以得到Contourlet系数。对于第k尺度、第l方向子带的Contourlet系数记为Ck,l，由于Contourlet变换的特点，Ck,l为一个矩阵，设该矩阵的每个元素为ci,j。阈值去噪方法就是对于给定的阈值λ，利用下面的公式对系数ci,j进行处理：

(6)

本文方法是通过Contourlet系数的相关性来确定阈值。首先给定一个整数N，用于定义邻域的大小。对于给定的系数ci,j，在矩阵中有一个对应的位置点(i,j)，定义该点的邻域窗口为

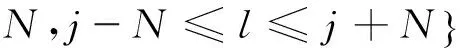
(7)

这样就可以计算点(i,j)在邻域Ai,j内的均方根振幅,即

(8)

定义相关系数ui,j为

(9)

式(9)表示系数ci,j和邻域内系数的相关性。根据这一相关系数，在每一点设定阈值为

(10)

这里λ是基本阈值。利用Donoho[14]的方法计算基本阈值，设M×N为当前系数所在方向子带的大小，则基本阈值为

(11)

式(11)中，σ为噪声标准方差。这就根据相关系数定义了自适应阈值，相应的自适应阈值函数为

(12)

这里的阈值λi,j在不同点是不同的，所以是自适应的。利用式(12)对Contourlet变换的每个方向子带进行处理，然后进行反变换就可以实现对地震数据中随机噪声的压制。

3 数值模拟

为了检验基于Contourlet系数相关性去噪方法的有效性，本文对小波变换、常规Contourlet变换阈值和本文的Contourlet邻域系数相关性去噪方法进行了对比性模拟实验。图3a为模拟的共炮点道集地震记录，图3b是加了100%随机噪声后的数据，信噪比为0.012 5;图3c为利用小波变换对图3b进行噪声压制后的数据，其信噪比提升为11.064 4；图3d为利

图3 几种去噪方法的对比实验

用常规Contourlet变换阈值法去噪后的数据，信噪比提升为11.512 4；图3e为利用本文的基于Contourlet邻域系数相关性去噪方法压制噪声后的数据，信噪比提升为12.275 5。由图3可以看出：小波变换去噪后的残余噪声是点状的，而Contourlet去噪后的残余噪声是线状的；无论小波变换还是Contourlet变换都可以较好地压制噪声和大幅度提高信噪比；在随机噪声压制方面，Contourlet方法优于小波变换，而本文的基于Contourlet系数相关性的方法优于常规Contourlet变换阈值方法。

应用基于Contourlet系数相关性去噪方法时，式(11)中的噪声标准方差σ对去噪结果有非常重要的影响。数值模拟时，由于噪声是已知的，该参数可以通过计算噪声的标准方差得到；对于实际资料，噪声是未知的，只能通过试验的方式来给定。当σ取值过大时，去噪过程会对有效信号产生损害;当σ取值过小时，去噪后的数据中将有较多的残留噪声。基于Contourlet系数相关性去噪方法不能去除掉所有随机噪声，残留的噪声以线状存在。由于Contourlet变换没有抗假频的能力，因而基于Contourlet系数相关性去噪方法也没有抗假频能力。基于Contourlet系数相关性去噪方法对原始噪声的信噪比没有严格的要求，一般信噪比达到0.1以上都可以用该方法进行处理;但是原始信噪比越高，处理后数据的信噪比也越高。

4 实际资料处理效果

利用本文基于Contourlet邻域系数相关性的去噪方法对一个实际单炮地震记录进行了处理，在处理前地震记录中可以看到较强的噪声(图4a)；处理后记录的整体面貌得到了很大改善，信噪比得以大幅度提高(图4b)；去除的噪声中有效信号很少(图4c)，说明该方法在去除噪声的同时很好地保留了有效信号。

利用本文基于Contourlet邻域相关性的去噪方法对一条测线进行了处理(图5)，在叠前对每一炮的地震数据进行去噪处理后进行叠加，对比处理前后的叠加剖面(图5a、b)可以看出，去噪后的叠加剖面同相轴更为连续，信噪比得到了显著提高。

图4 利用基于Contoulet系数相关性去噪方法处理单炮地震记录的效果

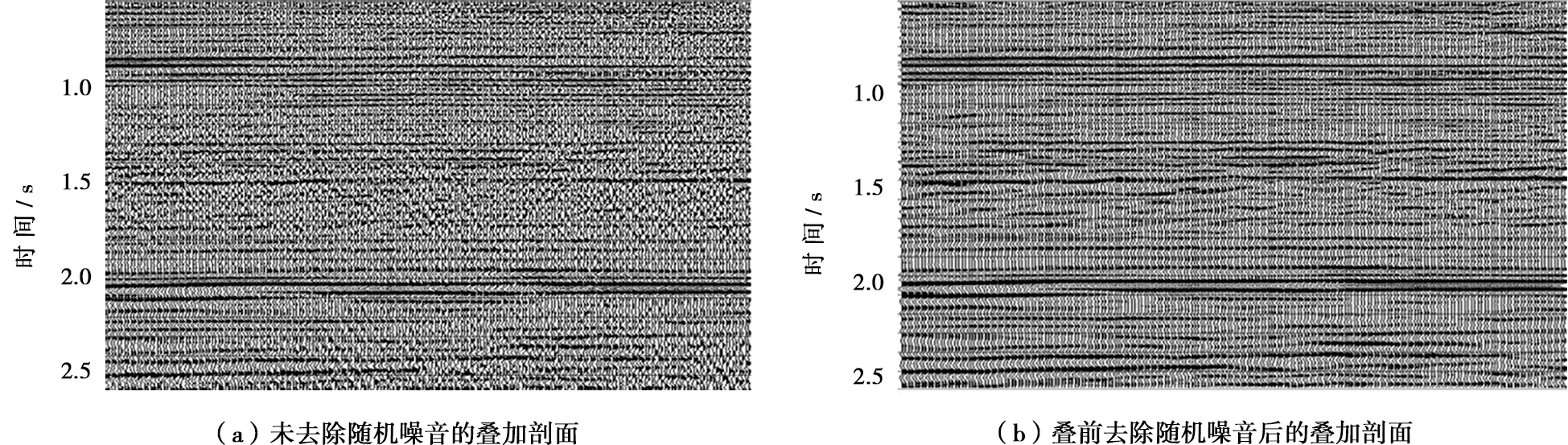
图5 利用基于Contourlet系数相关性去噪方法处理地震测线的效果

5 结束语

Contourlet变换是一种新型的二维图像处理方法，具有多分辨率、局部定位、多方向性等特点，能够对图像进行有效的稀疏表示。在Contourlet变换研究的基础上，提出了一种基于Contourlet邻域系数相关性的自适应阈值地震资料随机噪声压制方法，该方法利用地震数据在Contourlet域中其系数的相关性压制地震数据中的随机噪声。数值模拟资料和实际资料处理结果均表明，本文提出的去噪方法可以较好地压制叠前地震数据中的随机噪声，同时能够很好地保护有效信号。

[1] JONES I,LEVY S.Signal-to-noise ratio enhancement in multichannel seismic data via the Karhunen-Loeve transform[J].Geophysical Prospecting,1987,35(1):12-32.

[2] 康冶,于承业,贾卧,等.f-x域去噪方法研究[J].石油地球物理勘探,2003,38(2):136-138.

Kang Ye,Yu Chenye,Jia Wo,et al.The study on the denoising method in f-x domain[J].Oil Geophysical Prospecting,2003,38(2):136-138.

[3] YU S,CAI X,SU Y.Seismic signal enhancement by polynomial fitting[J].Applied Geophysics,1989,1(1):57-65.

[4] 吴亚东,符溪,文鹏飞,等.奇异值分解压制随机噪声的方法及应用[J].新疆石油地质,2004,24(2):144-145.

Wu Yadong,Fu Xi,Wen Pengfei,et al.SVD method and its application in attenuating random noise[J].Xinjiang Petroleum Geology,2004,24(2):144-145.

[5] 吴爱弟,牟永光.地震信号的小波包分解压噪方法[J].石油地球物理勘探，1998,33(4)：558-562.

Wu Aidi, Mou Yongguang.Seismic noise suppression using wavelet packet method[J].Oil Geophysical Prospecting,1998,33(4):558-562.

[6] 吴爱弟,曹思远.用正交多小波压制地震信号的随机噪声[J].石油地球物理勘探,2002,37(5):473-476.

Wu Aidi,Cao Siyuan.Random noise suppression of seismic signal using orthogonal multi-wavelets[J].Oil Geophysical Prospecting,2002,37(5):473-476.

[7] 张三宗,徐义贤.地震记录小波域高阶相关叠加技术[J].地球物理学报,2006,49(2):554-560.

Zhang Sanzong,Xu Yixian.Higher order correlative stacking for seismic data in the wavelet domain[J].Chinese Journal of Geophysics,2006,49(2):554-560.

[8] 高静怀,毛剑，满蔚仕,等.叠前地震资料噪声衰减的小波域方法研究[J].地球物理学报,2006,49(4):1155-1163.

Gao Jinghuai,Mao Jian,Man Weishi,et al.On the denoising method of prestack seismic data in wavelet domain[J].Chinese Journal of Geophysics,2006,49(4):1155-1163.

[9] 闫兴,杜启振,朱卫星.改进的第2代小波变换在地震资料去噪中的应用[J].勘探地球物理进展,2007,30(6)：455-458.Yan Xing,Du Qizhen,Zhu Weixing.Improved second-generation wavelet and its application in denoising of seismic data[J].Progress in Exploration Geophysics,2007,30(6):455-458.

[10] 王小品,贺振华，熊晓军.基于小波变换与奇异值分解的地震资料去噪新方法[J].石油天然气学报,2010,32(1)：232-236.

Wang Xiaopin,He Zhenghua,Xiong Xiaojun.Seismic data denoising new method based on wavelet transform and singular value decomposition method[J].Journal of Oil and Gas Technology,2010,32(1)：232-236.

[11] DO M N,VETTERLI M.The contourlet transform:an efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing,2005,53(1):1-16.

[12] 彭才,常智,韩朝军,等.基于Contourlet变换的地震噪声衰减[J].勘探地球物理进展,2008,31(4)：274-277.

Peng Cai,Chang Zhi,Han Zhaojun,et al.Noise suppression of seismic data based on Contourlet transform[J].Progress in Exploration Geophysics,2008,31(4):274-277.

[13] 张恒磊,李名勇,刘天佑.Contourlet域相关和阈值衰减联合去噪方法及其在地震资料处理中的应用[J].武汉大学学报·信息科学版,2011,36(9)：1047-1050.

Zhang Henglei,Li Mingyong,Liu Tianyou.Joint denoising of correlation and thresholding in Contourlet domain and its application to seismic data[J].Geomatics and Information Science of Wuhan University,2011,36(9)：1047-1050.

[14] DONOHO D L,JOHNSTONE I M.Ideal spatial adaption via wavelet shrinkage[J].Biometrika,1994,81(3):425-455.

(编辑：张喜林)

Seismic noise suppression method based on correlation of Contourlet coefficients

Wang Jianhua1,2Wang Shoudong3Liu Yanfeng3

(1.CNOOCResearchInstitute,Beijing100028,China; 2.NationalEngineeringLaboratoryforOffshoreOilExploration,Beijing100028,China; 3.StateKeyLaboratoryofPetroleumResourceandProspecting,ChinaUniversityofPetroleum,

Beijing102249,China)

In seismic signal sparse expressions of Contourlet transform, the relevance coefficients in transform domain have strong correlation. An adaptive threshold denoising method based on the correlation of Contourlet neighborhood coefficients is put forward. The neighborhood root-mean-square amplitude coefficients for every point are calculated with the method, the correlation of Contourlet neighborhood coefficients are calculated using the coefficients of the point and neighborhood root-mean-square amplitude and then the threshold according to the correlation of neighborhood coefficients is adaptively determined in this method. Numerical simulation and actual data processing results show the effectiveness of the proposed method, which indicates that it can protect the effective signal in suppressing noise.

Contourlet transform; random noise; seismic noise suppression; neighborhood coefficient correlation; self-adaption

王建花，女，高级工程师， 2006年毕业于中国海洋大学应用地球物理专业，获博士学位，现主要从事地球物理方法研究。地址：北京市朝阳区太阳宫南街6号院海油大厦B座(邮编：100028)。E-mail：wangjh7@cnooc.com.cn。

1673-1506(2016)01-0035-06

10.11935/j.issn.1673-1506.2016.01.005

P631.4+4

A

2015-02-01 改回日期：2015-04-20

*国家重点基础研究发展规划(973计划)“南海深水区复杂地质结构地震采集基础理论研究(编号：2009CB219403)” 、海洋石油勘探国家工程实验室“斜缆采集地震数据分析与处理技术研究”部分研究成果。

王建花,王守东,刘燕峰.基于Contourlet系数相关性的地震噪声压制方法[J].中国海上油气，2016,28(1)：35-40.

Wang Jianhua,Wang Shoudong,Liu Yanfeng.Seismic noise suppression method based on correlation of Contourlet coefficients[J].China Offshore Oil and Gas,2016,28(1):35-40.