内坑坑背系数对坑中坑基坑变形影响的敏感性分析

侯新宇，火映霞，薛必芳

(江苏开放大学建筑工程学院，南京　210036)



内坑坑背系数对坑中坑基坑变形影响的敏感性分析

侯新宇，火映霞，薛必芳

(江苏开放大学建筑工程学院，南京210036)

摘要：以苏州某地铁换乘站坑中坑为基本模型，采用土体卸载条件下的HS有限元模型，系统研究内坑坑背系数β对坑中坑基坑支护结构和基坑土体变形的影响。结果表明：外墙侧移随β增大而增大，β由0.125增大到0.75，外墙最大侧移增加34.08%，同时最大侧移位置下移了2.0 m，β对外坑底面附近以上的外墙墙身侧移影响较小，而对坑底以下侧移影响显著。内墙侧移随β增加而显著增大，β由0.125增大到0.75，内墙墙身最大侧移增加153.95%，最大侧移位置随β增大而下移，内墙墙顶竖向位移随β增大而减小。内坑坑底隆起、外坑坑底隆起随β增大而微弱减小，外坑坑背沉降总体随β增大而增大，但不同β值对应的沉降曲线相似。

关键词：坑背系数；坑中坑；变形影响；敏感性分析；HS模型

1概述

坑中坑基坑是在传统的大基坑底部开挖小基坑，作为一种独特的基坑形式伴随地下空间开发建设而大批量涌现，特别是在城市地下空间综合体、城市地铁换乘车站，以及超高层建筑地下部分等重要地下工程中，坑中坑基坑的安全可靠性直接关系到地下结构物自身安全以及周边建筑物等。坑中坑基坑的支护结构形式和土方施工特点有别于传统基坑，开挖卸载的土体应力场分布比传统基坑更为复杂[1-2]，常规基坑支护理论和最新的基坑工程设计规范均无法满足当前工程实际问题的需要，针对特殊基坑的变形影响研究更具现实意义[3-4]。

国内针对坑中坑的研究起步较晚，2005年龚晓南[5]最初对坑中坑问题进行归纳分类，后很多学者根据工程实践，对坑中坑从围护结构施工方法以及监测数据分析等角度进行研究[6-8]；陈乐意等[9]针对软土坑中坑的开挖计算深度选取、坑中坑位置对围护结构水平位移的影响进行数值模拟分析；申明亮等[10]对坑中坑基坑应力场进行参数化研究，最后确定影响最大的参数和最敏感应力区等结论；王洪新[11]把基坑宽度分为三类，并推导考虑基坑宽度影响的抗倾覆稳定安全系数计算公式；霍军帅等[12]通过离心模型试验研究了上海某异形坑中坑3种不同内外坑间距下内、外坑地下连续墙的变形规律；徐飞飞等[13]分析不同条件下坑中坑的内坑开挖对于外坑围护结构变形的影响，引入围护结构侧移影响率，以综合考虑内坑开挖对外坑的影响以及外坑围护结构的累计变形量大小；熊中华[14]利用ABAQUS有限元软件模拟坑中坑开挖，研究坑趾系数、深度比、面积比3个参数对外坑变形特征影响；丰土根等[15]通过数值模拟分析方法对悬臂式支护结构坑中坑基坑进行研究，得出坑中坑不同开挖位置、深度及大小对围护结构变形的影响规律。

以上研究中对坑中坑基坑坑背系数的深入研究内容则未见。以苏州地铁人民路换乘站为对象，系统研究坑中坑外墙坑背系数变化对基坑支护结构、基坑土体等变形特征的影响。

2坑中坑基坑参数的选取

如图1坑中坑基坑断面中，基本模型参数及尺寸为：外坑开挖深度H=16 m，外墙入土深度D=16 m，内外墙体距离B=16 m，内墙入土深度d=8 m，内坑开挖深度h=8 m。内坑坑背系数定义为内坑开挖深度与内外墙体距离的比值，即β=h/B。

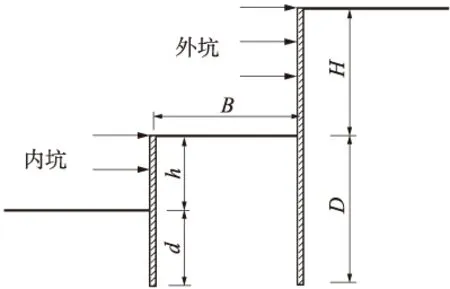
图1　坑中坑基坑断面示意

分析坑中坑支护基本模型参数H、D、B、d不变的情况下，内墙入土深度h单因素变化的情况下，即内坑坑背系数β(β=h/B)对基坑变形特征的单因素影响，见表1。

3坑中坑基坑数值模型

坑中坑基坑开挖卸载过程中，应采用土体卸载模量替代传统的加载模量，理想的弹塑性模型无法满足坑中坑要求。HS(Hardening-Soil Model)模型是一个考虑了土体剪胀性的塑性模型，在Mohr-Coulomb模型的屈服面基础上引入了一个屈服帽盖，即当对土体施加偏应力(σ1-σ3)时，土体表现出刚度下降，产生塑性应变，很多文献均证明HS模型能够很好地模拟基坑土体开挖。采用HS模型对坑中坑基坑进行数值模拟，模型参数采用三轴固结不排水剪(CU)的有效应力指标，土层物理力学性能参数见表2。

表2　土层计算参数

坑中坑断面外墙为0.80 m厚钢筋混凝土现浇地下连续墙，内墙为0.60 m厚地下连续墙，墙体力学参数见表3。外坑设置3道支撑，首道支撑为钢筋混凝土支撑，其余为φ609 mm(t=6 mm)钢管支撑；内坑设置2道φ609 mm(t=6 mm)钢管支撑，外坑支撑等效长度12.0 m，内坑支撑等效长度8.0 m，所有支撑水平间距均为6.0 m，支撑物理性质参数如表4所示。表2～表4中直接参数取自该项目工勘报告，间接参数由直接参数根据理论公式换算得到。典型断面基坑土体开挖工况共7个，采取先撑后挖的开挖方式，每次开挖深度到达下一支撑位置超挖1 m，坑外超载距离地连墙1 m，取20 kPa。有限元计算模型见图2。

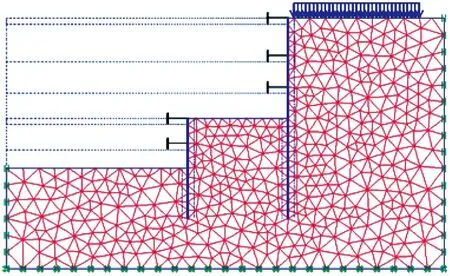
图2　有限元计算模型

C30混凝土厚/mm轴向刚度(EA)/(kN/m)抗弯刚度(EI)/(kN/m2/m)泊松比8002.4×1070.128×1070.1676001.8×1070.054×1070.167

表4　支撑物理力学参数

4内坑坑背系数β敏感性分析

以图2的基本模型作为参照，对表1选取的不同内坑开挖深度h进行有限元数值模拟计算，根据土体分步开挖卸载的计算结果，系统分析内坑坑背系数β变化对外墙侧向位移、内墙侧向位移、内坑坑底竖向位移、外坑坑底竖向位移、外坑坑背竖向位移产生的影响。

4.1内坑坑背系数β对外墙侧向位移的影响

图3为不同内坑坑背系数变化情况下的外墙最终侧移曲线。外墙墙身最大侧移随内坑开挖深度增加而增大，即随内坑坑背系数增加而增大(图4)，内坑开挖深度2 m时(即内坑坑背系数0.125)外墙最大侧移28.34 mm，而内坑开挖深度12 m时(即内坑坑背系数0.75)外墙最大侧移增大至38.00 mm，增大34.08%。外墙最大侧移位置随内坑坑背系数增大而下移(图5)，内坑坑背系数0.125时，最大侧移发生在15.33 m深度位置，当内坑坑背系数增大到0.75时，最大侧移位置发生在17.33 m深度位置，下移了2.0 m，位置由外坑坑底以上下降到坑底以下。内坑坑背系数对墙身最大侧移以上的侧移影响较小，而下部侧移影响显著，下部具有相似的侧移趋势(图3、图4)，而外墙墙顶侧移受内坑坑背系数影响甚微(图5)。

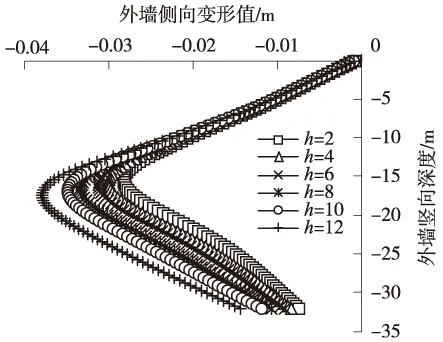
图3　外墙侧向位移曲线

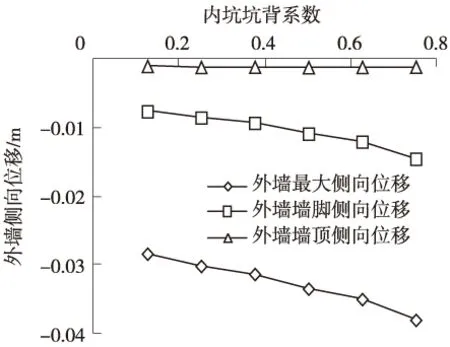
图4　外墙最大侧向位移值

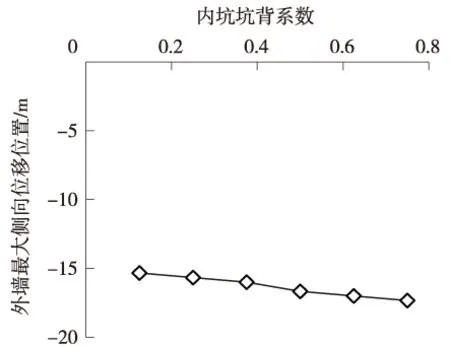
图5　外墙最大侧向位移位置

分析可知：内坑土体能为外墙提供被动土压力，随着内坑土体卸载，被动土压力减小，外墙侧移增大，但在外坑底面以上，因内支撑作用使外墙侧移受到限制。

4.2内坑坑背系数β对内墙侧向位移的影响

内坑坑背系数变化对内墙侧移影响很大(图6)，由于内坑开挖深度增大，导致内墙侧移整体随内坑坑背系数增加而增大(图7)。β从0.125逐渐增加到0.75时，内墙墙身最大侧移从14.10 mm逐渐增大到35.80 mm，增加153.95%，内墙墙顶侧移从14.10 mm逐渐增大到20.00 mm，增加41.97%，而墙角侧移变化不大(图7)。

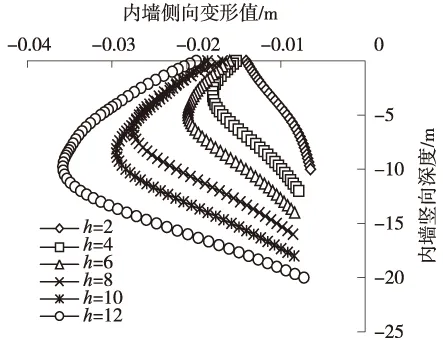
图6　内墙侧向位移曲线

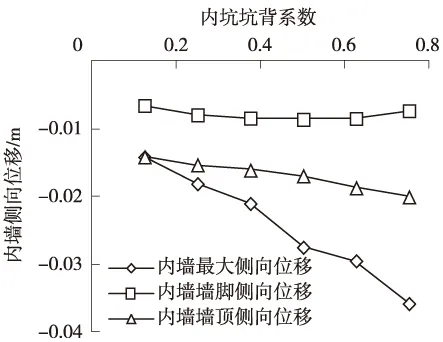
图7　内墙最大侧向位移值

内墙最大侧移位置随内坑坑背系数增大而呈线性下降(图8)，内坑开挖深度12 m(β=0.75)时，内墙最大位移处于深度9.75 m位置处。内墙墙顶竖向位移随内坑坑背系数增大而减小，β从0.125逐渐增加到0.75时，内墙墙顶竖向位移从46.39 mm逐渐减小到18.18 mm，减少60.82%(图9)。

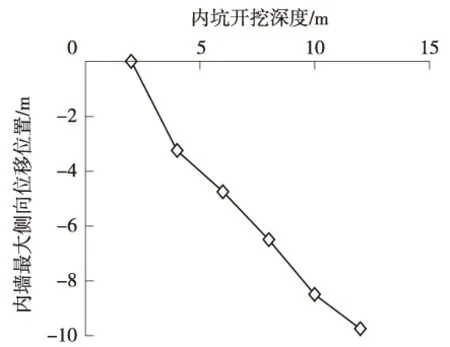
图8　内墙最大侧向位移位置

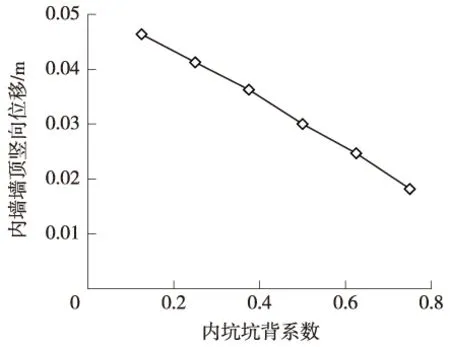
图9　内墙墙顶竖向位移值

4.3内坑坑背系数β对内坑坑底竖向位移的影响

由图10可知：内坑坑底竖向隆起有随β增大而微弱减小的趋势。β较大时，内坑坑底在内墙内侧附近出现轻微局部隆起，分析是因为β较大时内墙侧移较大，挤压内坑底部土体所导致。

4.4内坑坑背系数β对外坑坑底竖向位移的影响

外坑坑底竖向位移总体随着内坑坑背系数增大而减小(图11、图12)，但幅度较低。外坑坑底最大竖向位移位置出现在内墙外边缘和外墙内边缘，随着距离外墙接近，内坑坑背系数对对外坑坑底竖向位移影响逐渐减弱，到达外墙边缘已经几乎无影响，但外墙边缘依然出现显著的局部隆起，分析仍然是由于外墙侧移对土体挤压导致。

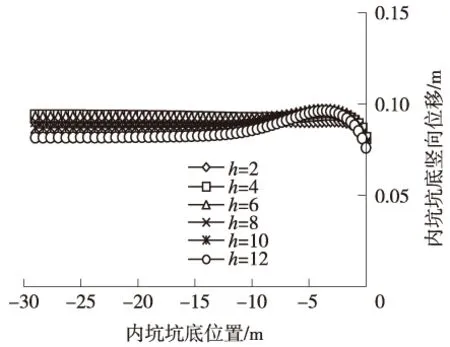
图10　内坑坑底竖向位移曲线

图11　外坑坑底隆起曲线

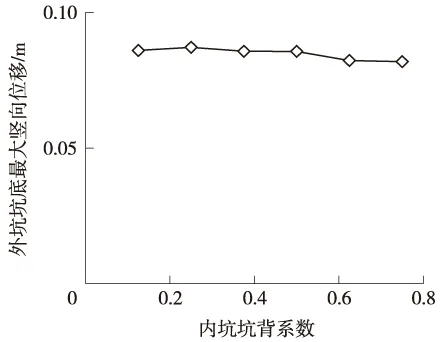
图12　外坑坑底最大隆起位置

4.5内坑坑背系数β对外坑坑背竖向位移的影响

外坑坑背土体在坑中坑最终开挖产生显著沉降(图13)，不同内坑坑背系数对应的沉降曲线相似，外坑坑背沉降随内坑坑背系数增大而增大。β从0.125逐渐增加到0.75时，外坑坑背最大沉降从43.77 mm逐渐增大到54.71 mm，增加约25.0%(图14)。

图13　外坑坑背沉降曲线

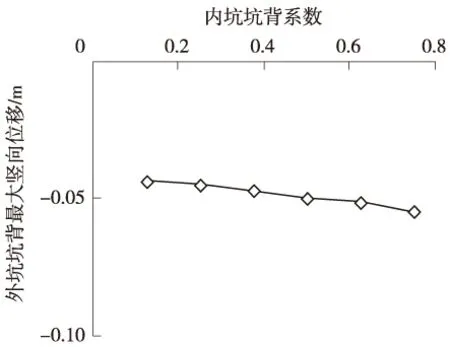
图14　外坑坑背最大沉降位置

5结语

通过对基本模型条件下的坑中坑开挖进行数值模拟分析发现，在苏州典型粉质黏土地质条件下，内坑坑背系数β变化坑中坑支护结构和土体的变形均产生不同程度影响，得出如下结论。

(1)外墙侧移随内坑坑背系数β增加而增大，β由0.125增大到0.75，外墙最大侧移增加34.08%，最大侧移位置由15.33 m深度处下移至17.33 m深度处，下移了2.0 m，位置由外坑坑底以上下降到坑底以下。β对外坑底面附近以上的外墙墙身侧移影响较小，而对坑底以下侧移影响显著，且坑底以下具有相似的侧移趋势。

(2)内墙侧移受β影响显著，整体随β增加而增大，β从0.125增加到0.75，内墙墙身最大侧移增加153.95%，内墙墙顶侧移增加41.97%，墙脚侧移变化不大。内墙最大侧移位置随β增大而下移。内墙墙顶竖向位移随β增大而减小，β从0.125增加到0.75，内墙墙顶竖向位移减少60.82%。

(3)内坑坑底隆起随β增大而微弱减小。β较大时，坑底在内墙内侧附近出现轻微局部隆起。

(4)外坑坑底隆起整体随β增大而轻微减小。最大隆起位置出现在内墙外边缘和外墙内边缘处，随着距离外墙接近，β对对外坑坑底竖向位移影响逐渐减弱，外墙边缘出现局部隆起。

(5)外坑坑背沉降总体随β增大而增大，但不同β值对应的沉降曲线相似。

参考文献：

[1]侯新宇，刘松玉，童立元.地铁换乘站”坑中坑”开挖变形特性研究[J].东南大学学报：自然科学版，2012，41(6):1289-1294.

[2]李守德，等.天然地基土在基坑开挖侧向卸荷过程中的模量计算[J]土木工程学报，2002，35(5):70-74.

[3]潘振华.超大型深基坑对高速铁路桥墩稳定性影响分析[J].铁道标准设计，2014，58(7):80-84.

[4]旷庆华.同深基坑开挖引起紧邻地铁车站变形特性研究[J].铁道标准设计，2015，59(5):130-133.

[5]龚晓南.关于基坑工程的几点思考[J].土木工程学报，2005，38(9):99-102.

[6]徐为民，屠毓敏，等.某工程坑中坑塌滑原因分析及加固设计[J].岩土力学，2010，31(5):1555-1559.

[7]金立坚，王志刚.“坑中坑”—高低跨深浅坑异形区间隧道的基坑施工技术[J].建筑施工，2005，27(9):5-7.

[8]吴铭炳，林大丰，戴一鸣，等.坑中坑基坑支护设计与监测[J].岩土工程学报，2006，28(S):1570-1572.

[9]陈乐意，李镜培，梁发云，等.坑中坑对基坑围护结构水平位移影响数值分析[J].岩土工程学报，2008，30(S):59-61.

[10]申明亮，廖少明，周小华.坑中坑基坑应力场的参数化分析[J].岩土工程学报，2010，8(S2):187-191.

[11]王洪新.基坑宽度对围护结构稳定性的影响[J].土木工程学报，2011，44 (6):120-126.

[12]霍军帅，宫全美，陈娟.坑中坑基坑围护结构变形特性分析[J].土木建筑与环境工程，2011，6(S1):139-143.

[13]徐飞飞，崔梓萍，徐意智，等.坑中坑的基坑变形分布及其变化规律[J].地下空间与工程学报，2012，7(S1):1376-1381.

[14]熊中华.坑中坑开挖影响下的基坑变形特性有限元分析[J].土木工程与管理学报，2013，30(6):57-61.

[15]丰土根，熊中华，余波.坑中坑开挖对悬臂式支护结构侧移的影响分析[J].岩土工程学报，2013，35(11):2053-2059.

Sensitivity Analysis of Impact of Internal Depth to Bottom Width Ratio on Deformation of Pit in Pit

HOU Xin-yu， HUO Ying-xia， XUE Bi-fang

(Department of Civil Engineering， JiangSu Open University， Nanjing 210036， China)

Abstract：Adopting Hardening-Soil finite element model with unloaded soil， this paper addresses the influence of the ratio β of internal depth to bottom width on the retaining structure and the deformation of the pit in pit based on the basic model of the pit of a metro transfer station in Suzhou. The results show that the lateral deformation of external wall increases with growing β and maximum value of 34.08% is added when β increases from 0.125 to 0.75， meanwhile the location moves downward 2.0 m; β has little effect on the lateral deformation near the above external pit bottom， but remarkably on the part under the pit bottom. The lateral deformation of internal wall increases obviously with growing β and the maximum value of 153.95% is added when β increases from 0.125 to 0.75， meanwhile the location moves downward， and the uplift of the internal wall reduces as well. The bottom uplift of the internal and external pit decreases slightly with growing β， while the settlement of the internal depth to bottom width tends to increase with growing β， but the settlement curves corresponding to different β are similar．

Key words：Ratio of internal depth to bottom width; Pits in foundation-pit; Deformation influence; Sensitivity analysis; HS (Harden-ing-Soil) model

中图分类号：U231+.4

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2016.04.021

文章编号：1004-2954(2016)04-0086-05

作者简介：侯新宇(1975—)，男，副教授，博士，注册土木工程师(岩土)，主要从事地下交通工程的理论研究和技术应用工作，E-mail:Houxy_geo@163.com。

基金项目：国家自然科学基金项目(41202203)；江苏省高校自然科学研究面上项目(14KJB560004)；江苏省“六大人才高峰”项目(2014JZ010)；江苏省“青蓝工程”项目

收稿日期：2015-08-13； 修回日期：2015-08-26