模糊团的一个注记

孙峰，屈小兵，汪天飞，张之鹤

模糊团的一个注记

孙峰1，2，屈小兵1，汪天飞1，张之鹤1

(1.乐山师范学院数学与信息科学学院，四川乐山614004;2.四川师范大学数学与软件科学学院，四川成都610066)

模糊图论中的模糊团推广图论中的团，在图论中，团导出的子图是完全的，然而根据现有模糊团的定义，模糊团导出的模糊子图不一定是完全的.这篇注记修正模糊团的概念，以保证其导出的模糊子图是完全的，并给出模糊团和极大模糊团的刻画.

模糊图;模糊团;完全性

图论中的图由若干给定的点及连接2点的边构成，是对象集合及对象与对象之间关系的数学表示.在图论中，这些对象以及对象间的关系都是分明的，然而在实际问题中，对象或对象间的关系往往存在不清晰、不确定的情形，因此需要模糊化的数学表示.自L.A.Zadeh［1］提出模糊集的概念以来，模糊集及其理论得到长足发展［2－3］.基于模糊集的定义，J.N.Mordeson［4］提出了模糊图的概念.随后研究者从理论和应用方面，不断丰富模糊图论.至今，模糊图论已经取得丰硕的成果［5］.应用方面，模糊图在信息科学［6］、神经网络［7－8］等方面有着重要的应用.理论方面，一些经典的图论概念及定理被推广到模糊图中［9－11］.众所周知，图论中的团是一个两两之间有边的顶点集合，即是说团导出的图是完全的.然而根据P.S.Nair等［12］对模糊团的定义，模糊团所导出的模糊子图并不是完全的(见例2.1).在这篇注记中，对模糊团的概念作了修正，以保证其导出的模糊子图是完全的.此外，还定义了模糊极大团和最大团，并讨论了它们的性质及刻画.

1 预备知识

首先，介绍一些符号与定义.对矩阵A，记其转置为AT，其第i行第j列的元素为Aij.令N={1，2，…，n}.记|X|为集合X的基数，对于任意2个集合X与Y，记X－Y={x∈X:x∉Y}，当Y={y}时，X－Y表示X－y.对区间［0，1］上的x、y，x∨y=max{x，y}，x∧y=min{x，y}.

定义1.1［13］设G=(V，E)为无向图，其中V是顶点的集合，E是边的集合，记连接顶点vi与vj的边为(vi，vj).顶点vi与vj相邻当且仅当(vi，vj)∈E.若图G=(V，E)中的任何2个顶点都是相邻的，则称G是完全图.图G'=(V'，E')称为图G=(V，E)的子图，若V'⊆V，E'⊆E.以图G的顶点集V的非空子集V1为顶点集，以两端点均在V1中的所有边为边集的G的子图称为由V1导出的子图.互不相同的顶点和边交替出现的序列v1，(v1，v2)，v2，(v2，v3)，v3，…，(vn－1，vn)，vn(简记为v1，v2，…，vn)称为从v1到vn的路径，路径中的边数称为路径的长度.起止顶点相同且长度大于等于3的路径称为圈.

定义1.2［13］设G=(V，E)为无向图，C为V的非空子集，若C中顶点两两相邻，则称C为团.若一个团不是其它任何团的子集，则称这个团是极大团.若一个团满足基数最大，则称这个团为最大团.

由定义1.2可知，图论中的团导出的子图是完全的.在一些文献中，研究者将完全图与团视为等同，在此区别对待二者.

记论域X上的所有模糊集合为F(X)={S:X→［0，1］}，X×Y上的所有模糊关系为F(X×Y)={R:X ×Y→［0，1］}.

定义1.3［5］设V是一个非空集合，δ∈F(V)，μ∈F(V×V)，若对任何x，y∈V有μ(x，y)≤δ(x)∧δ(y)，则称FG=(V，δ，μ)为模糊图，并称δ为FG的模糊顶点集合，μ为FG的模糊边的集合.

在本文中，所有涉及的模糊图FG=(V，δ，μ)均是无向的，即μ是对称的，且对任何x∈V有μ(x，x)=0.简便起见，记FG=(V，δ，μ)=(δ，μ)(除非特别指明，V代指n元集).记模糊图FG的底图为FG*=(δ*，μ*)，其中δ*={x∈V:δ(x)＞0}，μ*= {(x，y)∈V×V:μ(x，y)＞0}.对任意t∈［0，1］，定义模糊图FG=(δ，μ)的t－截集为FGt=(δt，μt)，其中δt={x∈V:δ(x)≥t}，μt={(x，y)∈V×V:μ(x，y)≥t}.

定义1.4［5］称模糊图FH=(ρ，ν)为模糊图FG=(δ，μ)的模糊子图，若ρ≤δ且ν≤μ.进一步，若ρ=δ，则称FH是FG=(δ，μ)的生成子图.

定义1.5［5］称模糊图FH=(P，ρ，ν)为模糊图FG=(V，δ，μ)由P导出的模糊子图，若P⊆V，ρ(x) =δ(x)，∀x∈P且ν(x，y)=μ(x，y)，∀x，y∈P.称FG的模糊子图FH=(V，ρ，ν)为由ρ导出的模糊子图，若FH是以ρ为模糊顶点集合的极大模糊子图，即ν(x，y)=ρ(x)∧ρ(y)∧μ(x，y)，∀x，y∈V.

定义1.6［5］模糊图FG=(δ，μ)中的路径P是由不同的顶点v1，v2，…，vn(n≥2)构成的序列且满足μ(vi，vi+1)＞0.路径中的边数称为路径的长度.FH =(ρ，ν)称为圈当且仅当(ρ*，ν*)是圈.FH=(ρ，ν)称为模糊圈当且仅当FH是圈且不存在唯一的(x，y)∈μ*使得μ(x，y)=∧{μ(u，v):(u，v)∈μ*}.

定义1.7［14］设FG=(δ，μ)为模糊图，若对任意(x，y)∈μ*有μ(x，y)=δ(x)∧δ(y)，则称FG是强的;若对任何x，y∈δ*(x≠y)有μ(x，y)=δ(x)∧δ(y)，则称FG是完全的.

显然，模糊完全图是强的，但反之不然.

定义1.8［12］设FH=(ρ，ν)为模糊图FG=(δ，μ)的模糊子图，若FH*是团且FH中的每一个圈都是模糊圈，则称FH为模糊团.

P.S.Nair等［12］将模糊团视为模糊子图，并给出了模糊团的如下刻画.

引理1.1［12］模糊图FG=(δ，μ)的模糊子图FH=(ρ，ν)是模糊团当且仅当FH中的每一个长度为3的圈都是模糊圈.

定义1.9［15］设Q∈F(X×Y)，S∈F(Y×Z)，则∨－∧合成Q⊙S∈F(X×Z)定义为

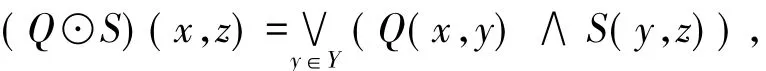
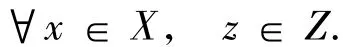
2 模糊团的修正及其刻画

图论中的团导出的图是完全的.然而根据定义1.8，模糊团所导出的模糊子图(即模糊团本身)并不是完全的.

例2.1考虑V={v1，v2，v3，v4}上的模糊图FG =(δ，μ)，其中δ(v1)=δ(v2)=δ(v3)=δ(v4)=1，μ(v1，v2)=0.5，μ(v1，v3)=0.8，μ(v1，v4)=0.8，μ(v2，v3)=0.5，μ(v2，v4)=0.5，μ(v3，v4)=0.7，如图1所示.

考虑如图2所示的模糊子图FH=(ρ，ν).

从引理1.1可知，FH是模糊团，但是0.8= ν(v1，v3)≠ρ(v1)∧ρ(v3)=1，即FH是不完全的.

下面对模糊团的概念进行修正.

定义2.1设FG=(δ，μ)为模糊图，ρ为δ的非空子集，若由ρ导出的模糊子图是完全的，则称ρ为模糊团.

注2.1P.S.Nair等［12］定义的模糊团本质上是模糊图，而定义2.1中的模糊团是模糊集，即模糊图顶点集合的子集.

例2.2考虑例2.1中的模糊图FG=(δ，μ)，容易验证ρ={ρ(v1)=0.8，ρ(v2)=0.5，ρ(v3)=0.8，ρ (v4)=0.7}是FG的模糊团，其导出的模糊子图FH =(ρ，ν)见图3.

为避免定义1.8与定义2.1混淆，将定义1.8中的模糊团称为NC－模糊团.下面讨论NC－模糊团，模糊团及模糊完全图之间的关系.

定理2.1模糊完全图是NC－模糊团.

证明令FH=(ρ，ν)为模糊完全图.设abca(a，b，c∈ρ*)为FH中长度为3的圈，因FH是完全的，则有ν(a，b)=ρ(a)∧ρ(b)，ν(b，c)=ρ(b)∧ρ(c)，ν(a，c)=ρ(a)∧ρ(c).从而ν(a，b)∧ν(b，c)∧ν(a，c)=ρ(a)∧ρ(b)∧ρ(c).不失一般性，假设ρ(a)=ρ(a)∧ρ(b)∧ρ(c)，于是ν(a，b)=ν(a，c)=ρ(a)，即abca是模糊圈.由引理1.1知FH是NC－模糊团.

推论2.1模糊团导出的模糊子图是NC－模糊团.模糊团导出的模糊子图是完全的，从而是NC－模糊团.

定理2.2强NC－模糊团是完全的.

证明令FH=(ρ，ν)为强NC－模糊团.显然FH*是团，则对任意a，b∈ρ*，有(a，b)∈ν*.因FH是强的，故有ν(a，b)=ρ(a)∧ρ(b).从而ν(a，b)= ρ(a)∧ρ(b)，∀a，b∈ρ*，即FH是完全的.

注2.2由定理2.2知，强NC－模糊团的顶点集合是模糊团.

定理2.3设FG=(δ，μ)为模糊图，ρ为δ的非空子集.ρ是模糊团当且仅当对任意x，y∈ρ*(x≠y)有ρ(x)∧ρ(y)≤μ(x，y).

证明设ρ是FG的模糊团，FH=(ρ，ν)是由ρ导出的模糊子图.显然，FH是完全的.从而由定义1.5与1.7，有ρ(x)∧ρ(y)=ν(x，y)=ρ(x)∧ρ(y)∧μ

(x，y)≤μ(x，y)，∀x，y∈ρ*.

反之，设ρ是δ的子集且满足ρ(x)∧ρ(y)≤μ(x，y)，∀x，y∈ρ*，x≠y.令FH=(ρ，ν)为由ρ导出的模糊子图.由定义1.5知，对任意x，y∈ρ*有ν(x，y)=ρ(x)∧ρ(y)∧μ(x，y)，则从假设ρ(x)∧ρ(y)≤μ(x，y)可知ν(x，y)=ρ(x)∧ρ(y).故FH是完全的，即ρ是模糊团.

推论2.2设ρ是模糊图FG=(δ，μ)的模糊团，则对任何t∈(0，1］，ρt是图FGt中的团.

证明设ρ是模糊图FG=(δ，μ)的模糊团.由定理2.3知ρ(x)∧ρ(y)≤μ(x，y)，∀x，y∈ρ*，x≠y.从而对任意2个顶点x，y∈ρt有μ(x，y)≥ρ(x)∧ρ(y)≥t，即(x，y)∈μt，故ρt是图FGt中的团.

推论2.3设ρ是模糊图FG=(δ，μ)的模糊团，则ρ的任意非空子集Q是FG的模糊团.

证明设ρ是模糊图FG=(δ，μ)的模糊团，Q为ρ的任意非空子集，则对任何x∈V有Q(x)≤ρ(x)，由定理2.3知结论成立.

对于模糊图FG=(δ，μ)，定义n×n的模糊矩阵MFG为

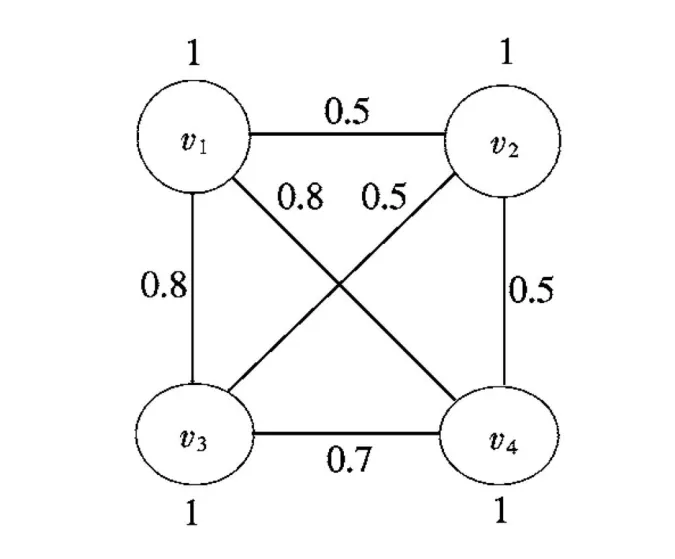
对于δ的非空子集ρ，定义n×1的模糊向量Vρ，

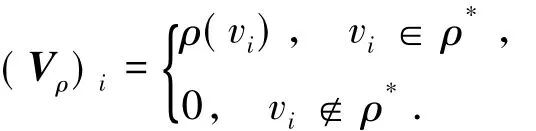
记XFG={X=(xi)，xi∈［0，1］:X⊙XT≤MFG}.

定理2.4若ρ是模糊图FG=(δ，μ)的模糊团，则Vρ∈XFG.反过来，对任意X=(xi)∈XFG，ρ(ρ(vi)=xi，∀i∈N)是模糊团.

证明设ρ是FG的模糊团，则由定理2.3知，对任何i，j∈N(i≠j)有(Vρ⊙)ij=(Vρ)i∧(Vρ)j=ρ(vi)∧ρ(vj)≤μ(vi，vj)=(MFG)ij，对任何i∈N有(Vρ⊙)ii=(Vρ)i∧(Vρ)i=ρ(vi)≤δ(vi)= (MFG)ii.从而Vρ∈XFG.

反过来，对任何X=(xi)∈XFG，构造ρ使得ρ(vi)=xi，∀i∈N.因为对任何i∈N，有ρ(vi)=xi≤(MFG)ii=δ(vi)，所以ρ≤δ.进一步，对任何i，j∈N(i≠j)，有ρ(vi)∧ρ(vj)=xi∧xj≤(MFG)ij=μ(vi，vj)，从而由定理2.3知ρ是FG的模糊团.

推论2.3说明模糊团的任意非空子集仍是模糊团.自然地，会考虑最大模糊团和极大模糊团.

定义2.2设ρ是模糊图FG=(δ，μ)的模糊团，若不存在模糊团σ使得ρ＜σ，则称ρ是极大的.进一步，称具有最大基数|ρ*|的极大模糊团ρ为最大模糊团.

例2.3考虑如图4所示的模糊图FG=(δ，μ).

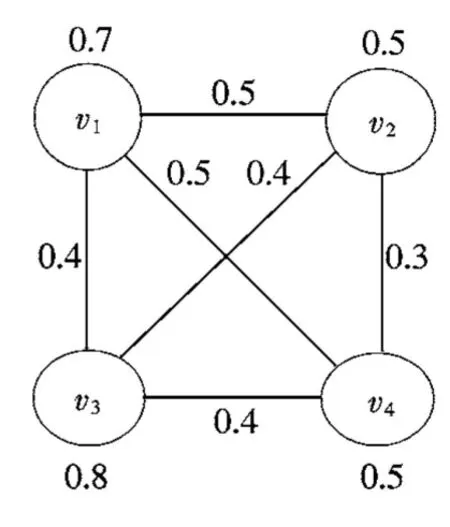
不难验证σ={σ(v1)=0.7，σ(v2)=0.3，σ(v3)= 0.4，σ(v4)=0.5}，Q={Q(v1)=0.7，Q(v2)=0.5，Q (v3)=0.4，Q(v4)=0.3}和ρ={ρ(v1)=0.4，ρ(v2)=0.3，ρ(v3)=0.8，ρ(v4)=0.4}都是FG的模糊团，并且都是最大的，而模糊团φ={φ(v1)=0.7，φ(v3)=0.4，φ (v4)=0.5}仅是极大的，而非最大的.

基于定理2.4，得到极大模糊团的如下刻画:

定理2.5设ρ是模糊图FG=(δ，μ)中δ的非空子集，ρ是极大模糊团当且仅当Vρ是XFG的极大元.

证明由定理2.4知ρ是模糊团当且仅当Vρ∈XFG.进一步，若ρ是极大的，则Vρ是XFG的极大元，反之亦然.

定理2.6设ρ是FG=(δ，μ)的极大模糊团，则

证明设ρ是FG=(δ，μ)的极大模糊团.由定理2.3知，ρ(x)∧ρ(y)≤μ(x，y)，∀x，y∈ρ*，从而有.下证ρ(vk)=μ(vi，vj).现设ρ(vk)＜μ(vi，vj)，定义模糊集σ使得除σ(vk)=μ(vi，vj)外有σ=ρ.显然σ＞ρ.此外，对任何z∈ρ*有σ(z)≤δ(vk)，即σ≤δ.下证σ是模糊团，即σ(y)∧σ(z)≤μ(y，z)，∀y，z∈ρ*.当vk∉{y，z}时，有σ (y)∧σ(z)=ρ(y)∧ρ(z)≤μ(y，z).若vk∈{y，z}，不失一般性，假设vk=z，则σ(y)∧σ(z)=ρ(y)∧μ.由此可知σ是模糊团，这与ρ的极大性矛盾.从而

推论2.4设ρ是FG=(δ，μ)的极大模糊团，FH=(ρ，μ)是由ρ导出的模糊子图且=μ(vi，vj)，则μ(vi，vj)=μ(vi，vj).

证明显然ν(vi，vj)≤μ(vi，vj).若ν(vi，vj)＜μ (vi，vj)，则ρ(vi)∧ρ(vj)=ν(vi，vj)＜μ(vi，vj).从而这与定理2.6相悖，于是ν(vi，vj)=μ(vi，vj).

定理2.7设ρ是FG=(δ，μ)的极大模糊团，则至少存在一x∈ρ*使得ρ(x)=δ(x).

证明设ρ是FG=(δ，μ)的极大模糊团.显然，ρ(x)≤δ(x)，∀x∈ρ*.假设对任何x∈ρ*有ρ(x)＜δ，则有ρ*=V1∪V2.一方面，若V1=ρ*，任取x0∈V1构造模糊集σ使得当x≠x0时σ(x)=ρ(x)且σ(x0)=δ(x0)，则知σ＞ρ.进一步，当x∈V1－x0时，有σ(x)∧σ(x0)=ρ(x)∧σ(x，x0);对任何x，y∈V1－x0有σ(x)∧σ(y)=ρ(x)∧ρ(y)≤μ(x，y)，故由定理2.3知σ是模糊团.而σ＞ρ，这与ρ是极大的矛盾.另一方面，若V1≠ρ*，即V2≠Ø，取x0∈V2使得ρ(x0)=max{ρ(x):x∈V2}，构造模糊集Q使得除Q(x0)=δ(x0)外有Q(x)=ρ (x)，则有Q＞ρ.下证Q是模糊团.当x∈V1时，有Q (x)∧Q(x0)=ρ(x)∧δ(x0)≤≤μ(x，x0)∧δ(x0)≤μ(x，x0);当x∈V2时，有Q (x)∧Q(x0)=ρ(x)∧δ(x0)=ρ(x)=ρ(x)∧ρ(x0)≤μ(x，x0);当x，y∈ρ*－x0时，有Q(x)∧Q(y)= ρ(x)∧ρ(y)≤μ(x，y)，从而由定理2.3知，Q是模糊团且Q＞ρ，矛盾!所以ρ(x)＜δ(x)对所有x∈ρ*并不成立.于是至少存在一x∈ρ*使得ρ(x)=δ(x).

在这里我们指出定理2.6、2.7和推论2.4的逆命题并不成立，见例2.4.

例2.4考虑例2.3中的模糊图FG=(δ，μ).易知φ={φ(v1)=0.7，φ(v2)=0.3，φ(v3)=0.3，φ(v4)= 0.3}是模糊团.设FH=(φ，ν)为由φ导出的模糊子图.不难发现μ(y，z)=μ(v2，v3)，ν(v2，v3)=μ(v2，v3)，φ(v1)=δ (v1).然而，σ={σ(v1)=0.7，σ(v2)=0.3，σ(v3)=0.4，σ(v4)=0.5}和Q={Q(v1)=0.7，Q(v2)=0.5，Q(v3)=0.4，Q(v4)=0.3}均为比φ大的模糊团，也即是说φ并非极大的.

致谢乐山师范学院科研项目(Z1402)对本文给予了资助，谨致谢意.

［1］ZADEH L A.Fuzzy sets［J］.Information and Control，1965，8:338－353.

［2］ZIMMERMANN H J.Fuzzy Set Theory and Its Applications［M］.Berlin:Springer－Verlag，2001.

［3］莫智文，舒兰，许彪.模糊数学理论及其应用评述［J］.四川师范大学学报(自然科学版)，1998，21(3):330－335.

［4］MORDESON J N.Fuzzy graphs［C］//Fuzzy Sets and their Applications to Cognitive and Decision Processes.New York:Academic Press，1975:77－95.

［5］MORDESON J N，NAIRP S.Fuzzy Graphs and Fuzzy Hypergraphs［M］.Berlin:Springer－Verlag，2000.

［6］GOMEZ D，MONTERO J，YANEZ J.A coloring fuzzy graph approach for image classification［J］.Information Sciences，2006，176:3645－3657.

［7］BHATTACHARYYA M，BANDYOPADHYAY S.Solving maximum fuzzy clique problem with neural networks and its applications［J］.Memetic Computing，2009，1:281－290.

［8］SUNITHA M S，KJUMAR A V.Fuzzy graphs in fuzzy neural networks［J］.Proyecciones J Mathematics，2009，28:239－252.

［9］MATHEW S，SUNITHA M S.Types of arcs in a fuzzy graph［J］.Information Sciences，2009，179:1760－1768.

［10］MATHEW S，SUNITHA M S.Node connectivity and arc connectivity of a fuzzy graph［J］.Information Sciences，2010，180:519－531.

［11］MATHEW S，SUNITHA M S.Menger’s theorem for fuzzy graphs［J］.Information Sciences，2013，222:717－726.

［12］NAIR P S，CHENG S C.Cliques and fuzzy cliques in fuzzy graphs［C］//Joint 9th IFSA World Congress and 20th NAFIPS International Conference，2001，4:2277－2280.

［13］WEST D B.Introduction to Graph Theory［M］.Upper Saddle River:Prentice Hall，2001.

［14］SUNITHA M S，KUMAR A V.Complements of fuzzy graphs［J］.Indian J Pure Appl Math，2002，33:1451－1464.

［15］NOLA A D，SESSA S，PEDRYCZ W，et al.Fuzzy Relation Equations and Their Applications to Knowledge Engineering［M］.Boston:Kluwer Academic Publishers，1989.

A Note on Fuzzy Cliques

SUN Feng1，2，QU Xiaobing1，WANG Tianfei1，ZHANG Zhihe1
(1.College of Mathematics and Information Science，Leshan Normal University，Leshan 614004，Sichuan; 2.College of Mathematics and Software Science，Sichuan Normal University，Chengdu 610066，Sichuan)

Fuzzy cliques in fuzzy graphs generalize cliques in graphs.In graph theory，a subgraph induced by a clique is complete.However，according to the existing definition of fuzzy cliques，the fuzzy subgraph induced by a fuzzy clique may not be complete.In this note，we modify the definition of a fuzzy clique so that the fuzzy subgraph induced by each fuzzy clique is complete.Then，fuzzy cliques and maximal fuzzy cliques are characterized.

fuzzy graphs;fuzzy cliques;completeness

O159

A

1001－8395(2016)03－0309－05

10.3969/j.issn.1001－8395.2016.03.001

(编辑郑月蓉)

2015－08－11

四川省教育厅科研项目(16ZB0297和16TD0029)

孙峰(1985—)，男，博士生，主要从事模糊关系、模糊算子、格上关系方程理论等研究，E－mail:sunfeng1005@163.com

2010 MSC:03E72;05C72