非交换环上的强余挠模
2016-06-05胡晴王芳贵熊涛
胡晴,王芳贵,熊涛
非交换环上的强余挠模
胡晴,王芳贵*,熊涛
(四川师范大学数学与软件科学学院,四川成都610066)
设R是任何环,L是R-模.若对任何平坦维数有限的模M,有Ext1R(M,L)=0,则L称为强余挠模.证明(F∞,SC)是余挠理论当且仅当l.FFD(R)<∞,其中F∞和SC分别表示平坦维数有限的模类和强余挠模类.还证明若w.gl.dim(R)<∞,则强余挠模是内射模.最后证明每一R-模是强余挠模当且仅当R是左完全环,且l.FFD(R)=0.
余挠模;强余挠模;平坦维数;左完全环;环的弱finitistic维数
1 预备知识
本文恒设R是有单位元的结合环,所有的模均指左模.用fdRL和pdRL分别表示R-模L的平坦维数和投射维数;gl.dim(R)和w.gl.dim(R)分别表示环R的整体维数和弱整体维数.
D.K.Harrison[1]为了刻画非有限的Abelian群的结构性质,引入了余挠模的概念.R-模C称为余挠模,是指对一切平坦模F,都有Ext1R(F,C)=0.其后E.E.Enochs[2]对余挠模的刻画做了大量的研究工作.J.Z.Xu[3]系统地讨论了余挠模的相关性质,证明了平坦模类F与余挠模类C二者构成了余挠理论,还证明了每个R-模是余挠模当且仅当环R是左完全环.L.Bican等[4]解决了平坦盖的猜测,即证明了对任何环R,每一R-模都有平坦盖;等价于说,每一R-模都有余挠包.
余挠模的研究按照平坦维数在进一步发展.S.B.Lee[5]引入弱内射模来刻画几乎完全整环.R-模W称为弱内射模,是指对任何平坦维数不超过1的模M,都有Ext1R(M,W)=0.交换环R称为几乎完全环,是指R的任何真商环都是完全环[6].借助于弱内射模,文献[7-9]证明了整环R是几乎完全整环,当且仅当平坦维数不超过1的模的投射维数也不超过1;当且仅当可除模是弱内射模.
E.E.Enochs等[10]按照余挠模的研究思路考察了更一般的情形,他们称之为n-余挠模.不过n-余挠模的不同的定义在文献[11]已经出现,熊涛[12]遵循S.B.Lee[5]的思路,把Enochs意义下的n-余挠模称为Ln-内射模.R-模L称为Ln-内射模,是指对任何平坦维数不超过n的模M,都有Ex(M,L)=0.
在这些研究的基础上,讨论文献[3]引入的强余挠模.R-模L称为强余挠模,是指对任何平坦维数有限的模M,都有Ext1R(M,L)=0.D.Bennis等[13]证明了若R是交换环,则每一R-模是强余挠模当且仅当R是完全环.H.Y.Yan[14]在一般的非交换环上也讨论了强余挠模的性质.本文借助环的弱finitistic维数来刻画强余挠模的相关性质.
2 强余挠模的基本性质
定义2.1[3]设L是R-模.若对任何平坦维数有限的模M有
Ext1R(M,L)=0,则L称为强余挠模.
例2.21)显然,内射模是强余挠模;
2)对任何n≥0,强余挠模是Ln-内射模.因此,强余挠模是弱内射模(自然也余挠模).
命题2.3对任何R-模L,以下等价:
1)L是强余挠模;
3)形如0→L→B→C→0的正合列是分裂的,其中fdRC<∞;
4)若0→A→B→C→0是正合列,其中fdRC<∞,则
0→HomR(C,L)→HomR(B,L)→HomR(A,L)→0也是正合列.
证明1)⇒2)设0→A→P→M→0是正合列,其中P是投射模.于是对任何k≥1有
ExtkR(A,L)≌Extk+1R(M,L).
注意fdRA<∞.于是断言由对k使用归纳法即证.
2)⇒1)显然.
1)⇔3)由文献[15]的推论7.20即知.
1)⇒4)由Ext1R(C,L)=0即得.
4)⇒1)考虑正合列0→A→P→C→0,其中P是投射模.于是

是正合列.由假设得到正合列
0→Ext1R(C,L)→0,
因此有Ext1R(C,L)=0,即L是强余挠模.
命题2.4设0→A→B→C→0是正合列.若A是强余挠模,则B是强余挠模当且仅当C是强余挠模.
证明设M是R-模,fdRM<∞,由正合列
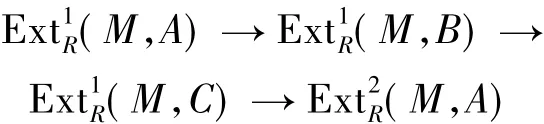
并引用命题2.3的2)即得.
命题2.5设{Li}是一簇R-模,则∏iLi是强余挠模当且仅当每一Li是强余挠模.
证明设M是R-模,fdRM<∞.由同构关系即得所证.

下面给出强余挠模是内射模的一个充分条件.
定理2.6设L是强余挠模.若fdRL<∞,且fdRE(L)<∞,其中E(L)是模L的内射包,则L是内射模.
证明考虑正合列0→L→E(L)→C→0,由条件有fdRC<∞.由命题2.3,此正合列分裂,因此有L是内射模.
因此,可以得到如下推论:
推论2.7若w.gl.dim(R)<∞,则每一强余挠模是内射模.
在文献[16]中定义了模的余挠维数和环的整体余挠维数(cot.D(R)).相应地,在文献[13]中也定义了模的强余挠维数和环的整体强余挠维数S.cot.D(R).由于w.gl.dim(R)<∞时强余挠模就是内射模,故得到下面的结果.
推论2.8[16]若w.gl.dim(R)<∞,则
gl.dim(R)=S.cot.D(R).
回顾环R称为左IF环,是指每一内射R-模是平坦模[17].由定理2.6,可以得到以下推论.
推论2.9若R是左IF环,L是强余挠模,且fdRL<∞,则L是内射模.
3 模类F∞与模类SC
设(A,B)是一个模类对.记
A⊥={B∈RM|对任何A∈A,Ex(A,B)=0},以及
⊥B={A∈RM|对任何B∈B,Ex(A,B)=0}.若A=⊥B,且B=A⊥,则(A,B)称为一个余挠对或一个余挠理论.J.Z.Xu[3]证明了平坦模类与余挠模类(F,C)构成了余挠理论.S.B.Lee[5]证明了平坦维数不超过1的模类与弱内射模类(F1,WI)构成了余挠理论.更一般地,用Fn表示平坦维数不超过n的模类,Ln表示Ln-内射模类,熊涛[12]证明了(Fn,Ln)构成了余挠理论.用F∞表示平坦维数有限的模类,SC表示强余挠模类.由定义2.1知SC= F∞
⊥,F∞⊆⊥SC.下面证明一般地有(F∞,SC)不构成余挠理论.
命题3.1
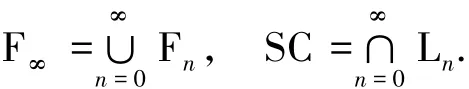
证明第一个等式是显然的,第二个等式在文献[10]中已经指出.
定义3.2[18]环R的弱finitistic维数定义为

命题3.3若l.FFD(R)=∞,则存在R-模M,使得fdRM=∞,但对任何L∈SC有

证明由条件l.FFD(R)=∞,有对任何正整数n,存在R-模Mn,使得fdRMn=n.令
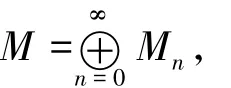
则

由于对任何L∈SC,有Ext1R(Mn,L)=0,因此有

推论3.4若l.FFD(R)=∞,则(F∞,SC)不构成余挠理论.
引理3.5设R为环,F∞=⊥SC当且仅当F∞在直和下封闭.
证明参见文献[14]的命题2.14.
文献[14]证明了(F∞,SC)构成余挠理论当且仅当F∞在直和下封闭.也可以用弱finitistic维数给出(F∞,SC)何时构成余挠理论的刻画.为此,需要下面的引理.
引理3.6设n是自然数,M和L是R-模,则:
1)M∈Fn当且仅当对任何
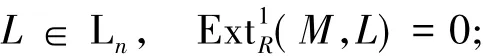
2)L∈Ln当且仅当对任何证明参见文献[12].

定理3.7对环R,以下各条等价:
1)l.FFD(R)<∞;
2)存在自然数n,使得Fn=F∞;
3)存在自然数n,使得Ln=SC;
4)存在自然数n,使得每一Ln-内射模是强余挠模;
5)(F∞,SC)构成余挠理论.
证明1)⇒2)设l.FFD(R)=n,则当fdRM<∞时,就有fdRM≤n.由此得到Fn=F∞.
2)⇒3)显然,这是因为
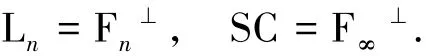
3)⇒4)这是平凡的.
4)⇒1)设M是R-模,fdRM<∞,则对任何L∈Ln,由条件,L是强余挠模,故由引理3.6,fdRM≤n.于是有l.FFD(R)≤n<∞.

2)+3)⇒5)由文献[12],(Fn,Ln)构成余挠理论.
5)⇒1)由推论3.4可知.
对定理3.7的证明作适当变更,容易得以下定理.
定理3.8设n是自然数,对环R,以下各条等价:
1)l.FFD(R)≤n;
2)Fn=F∞;
3)Ln=SC;
4)每一Ln-内射模是强余挠模.
推论3.9每一余挠模是强余挠模当且仅当l.FFD(R)=0.
推论3.10每一R-模是强余挠模当且仅当R是左完全环,且l.FFD(R)=0.
证明若每一R-模是强余挠模,则每一R-模是余挠模.由文献[3]的命题3.3.1,R是左完全环.由推论3.9,l.FFD(R)=0.
反之,设R是左完全环,且l.FFD(R)=0.设C是任何R-模,M是R-模,fdRM<∞.由于

[1]HARRISON D K.Infinite abelian groups and homological methods[J].Ann Math,1959,69(2):366-391.
[2]ENOCHS E E.Flat Covers and flat cotorsion modules[J].Proc AMS,1984,92(2):179-184.
[3]XU J Z.Flat Covers of Modules[M].New York:Springer-Verlag,1996.
[4]BICAN L,BASHIR E,ENOCHS E E.All modules have flat covers[J].Bull London Math Soc,2001,33:385-390.
[5]LEE S B.Weak-injective modules[J].Commum Algebra,2006,34:361-370.
[6]BAZZONI S,SALCE L.Almost perfect domain[J].Colloq Math,2003,95:285-301.
[7]FUCHS L,LEE S B.Weak-injectivity and almost perfect domains[J].J Algebra,2009,321:18-27.
[8]FUCHA L,LEE S B.On weak-injective modules over integral domains[J].J Algebra,2010,323:1872-1878.
[9]SALCE L.Almost perfect domains and their modules[C]//Commutaive Algebra.New York:Springer-Verlag,2010:363-386.
[10]ENOCHS E E,HUANG Z Y.Injective envelopes and(Gorenstein)flat covers[J].Algebra Rep Theory,2012,15:1131-1145.
[11]MAO L X,DING N Q.Relative cotorsion modules and relative flat modules[J].Commum Algebra,2006,34:2303-2317.
[12]熊涛.Ln-内射模与Ln-内射维数[D].成都:四川师范大学,2015.
[13]BENNIS D,JHILAL A.Strongly cotorsion dimension[J].Advances in Algebra,2009,2(1):31-37.
[14]YAN H Y.Strongly cotorsion(torsion-free)modules and cotorsion pairs[J].Bull Korean Math,2010,47(5):1041-1052.
[15]ROTMAN J J.An Introduction to Homological Algebra[M].London:Academic Press,1979.
[16]MAO L X,Ding N Q.The cotorsion dimension of modules and rings[C]//A Series of Lecture Notes in Pure and Applied Mathematics.Boca Raton:Chapamn Hall/CRC,2006:217-233.
[17]JAIN S.Flat and FP-injective[J].Proc AMS,1973,41(2):437-442.
[18]BASS H.Finitistic dimension and a homological generalization of semi-primary rings[J].Trans AMS,1960,95:466-488.
[19]JENSEN C U.On the vanishing of[J].J Algebra,1970,15:155-166.
[20]KAPLANSKY I.Commutative Rings[M].Revised Ed.Chicago:Univ of Chicago Press,1974.
[21]熊涛,王芳贵,胡葵.余纯投射模与CPH环[J].四川师范大学学报(自然科学版),2013,36(2):198-200.
[22]王芳贵.交换环与星型算子理论[M].北京:科学出版社,2006.
Strongly Cotorsion Modules over Non-commutative Rings
HU Qing,WANG Fanggui,XIONG Tao
(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
Let R be a ring and L an R-module.If Ext1R(M,L)=0 for all R-module M with finite flat dimension,then L is called strongly cotorsion.In this paper,it is shown that(F∞,SC)is a cotorsion theory if and only if l.FFD(R)<∞,where F∞and SC denote respectively the class of modules with finite flat dimension and the class of strongly cotorsion modules.It is also shown that if w.gl.dim (R)<∞,then all strongly cotorsion modules are injective.It is finally proved that every R-module is strongly cotorsion if and only if R is left perfect with l.FFD(R)=0.
cotorsion module;strongly cotorsion module;flat dimension;left perfect ring;weak finitistic dimension of a ring
O154
A
1001-8395(2016)03-0314-04
10.3969/j.issn.1001-8395.2016.03.002
(编辑陶志宁)
2014-08-30
国家自然科学基金(11171240)和教育部博士点专项科研基金(20125134110002)
*通信作者简介:王芳贵(1955—),男,教授,主要从事交换代数、同调代数与代数K-理论的研究,E-mail:wangfg2004@163.com
2010 MSC:16D50;16E10;16E30
