Double Biproduct Hom-Bialgebra and Related Quasitriangular Structures∗

Tianshui MA Haiying LI Linlin LIU

1 Introduction

Hom-structures(Lie algebras,algebras,coalgebras and Hopf algebras)have been intensively investigated in the literature recently(see[2,4,6,9,12–15,21–26]).Hom-algebras are generalizations of algebras obtained by a twisting map,which were introduced for the first time in[14]by Makhlouf and Silvestrov.The associativity is replaced by Hom-associativity,and Hom-coassociativity for a Hom-coalgebra can be considered in a similar way.

In[21,25],Yau introduced and characterized the concept of module Hom-algebras as a twisted version of usual module algebras,and the dual version(i.e.,comodule Hom-coalgebras)was studied by Zhang in[27].Based on Yau’s definition of module Hom-algebras,the first two authors and Yang in[9]constructed the smash product Hom-Hopf algebra(A?H,α⊗β)generalizing the Molnar’s smash product(see[16]),gave the cobraided structure(in the sense of Yau’s definition in[24])on(A?H,α ⊗ β),and also considered the case of twist tensor product Hom-Hopf algebra.Makhlouf and Panaite defined and studied a class of Yetter-Drinfeld modules over Hom-bialgebras in[12]and derived the constructions of twistors,pseudotwistors,twisted tensor product and smash product in the setting of Hom-case.Especially,in[6],we obtained the following result:Let(H,β)be a Hom-bialgebra such that β2=idH,and(A,α)be a left(H,β)-module Hom-algebra and a left(H,β)-comodule Hom-coalgebra.(,α⊗β)is a Radford’s biproduct Hom-bialgebra if and only if(A,α)is a Hom-bialgebra in the left-left Hom-Yetter-Drinfeld category.In[23],Yau introduced a twisted generalization of quantum groups,called quasitriangular Hom-bialgebras.They are non-associative and non-coassociative analogues of Drinfeld’s quasitriangular bialgebras.Each quasitriangular Hom-bialgebra comes with a solution of the quantum Hom-Yang-Baxter equation,which is a non-associative version of the quantum Yang-Baxter equation.Solutions of the Hom-Yang-Baxter equation can be obtained from modules of suitable quasitriangular Hom-bialgebras.

As we all know,the Radford biproduct plays an important role in the lifting method for the classification of finite dimensional pointed Hopf algebras(see[1]).Some related results about Radford’s biproduct have recently been given in[3,7–8,10,18].Let H be a bialgebra.A is a bialgebra in the left-left Yetter-Drinfeld categoryand B is a bialgebra in the right-right Yetter-Drinfeld category.In[11],Majid gave a construction of bialgebraby combining the two-sided smash product algebra Awith the two-sided smash coproduct coalgebra A×H×B,which generalizes the Radford biproduct bialgebra.

In this paper,we generalize the Majid’s double biproduct to the Hom-setting,and on the other hand,quasitriangular smash coproduct Hom-Hopf algebras are constructed.This is dual to the results in[9].

This article is organized as follows.In Section 2,we recall some definitions and results which will be used later.In Section 3,we give the right version of Radford’s biproduct Hombialgebra(,αA⊗β)and Hom-Yetter-Drinfeld categoryin[6].We also introduce the notions of two-sided smash product Hom-algebra(,αA⊗β⊗αB)and two-sided smash coproduct Hom-coalgebra(,αA⊗β⊗αB).Then we derive the necessary and sufficient conditions for(,αA⊗β⊗αB)and,αA⊗β⊗αB)to be a Hom-bialgebra,which is called double biproduct Hom-bialgebra and denoted by(,αA⊗β⊗αB),generalizing the Majid’s double biproduct bialgebra.Note that the construction of(,αA⊗ β ⊗ αB)here is different from that defined by Makhlouf and Panaite in[13].Section 4 is devoted to deriving the necessary and sufficient conditions for the smash coproduct Hom-Hopf algebra(,αA⊗β)to be quasitriangular.A concrete example for quasitriangular smash coproduct Hom-Hopf algebra is given in Section 5.

2 Preliminaries

Throughout this paper,we follow the definitions and terminologies in[9,21,23,27],with all algebraic systems assumed to be over the field K.Given a K-space M,we write idMfor the identity map on M.

We now recall some useful definitions.

Hom-algebraA Hom-algebra is a quadruple(A,μ,1A,α)(abbr.(A,α)),where A is a K-linear space,μ:A⊗A −→A is a K-linear map,1A∈A,and α is an automorphism of A,such that

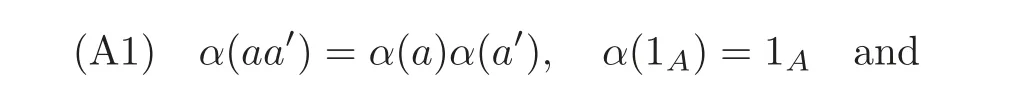
are satisfied for a,a?,a??∈ A.Here we use the notation μ(a ⊗ a?)=aa?.

Hom-coalgebraA Hom-coalgebra is a quadruple(C,Δ,εC,β)(abbr.(C,β)),where C is a K-linear space,Δ :C −→ C ⊗C,εC:C −→ K are K-linear maps,and β is an automorphism of C,such that

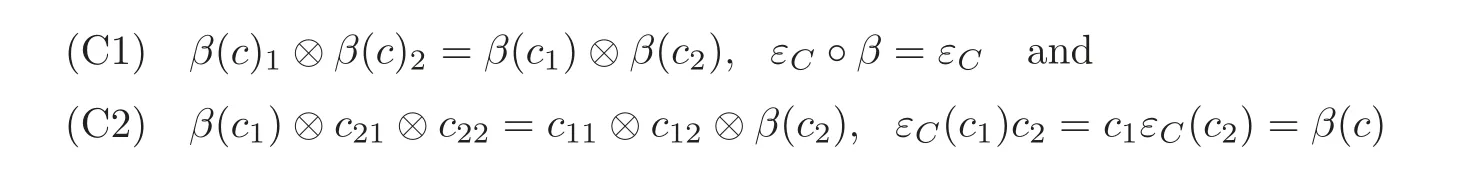
are satisfied for c ∈ A.Here we use the notation Δ(c)=c1⊗ c2(summation implicitly understood).

Hom-bialgebraA Hom-bialgebra is a sextuple(H,μ,1H,Δ,ε,γ)(abbr.(H,γ)),where(H,μ,1H,γ)is a Hom-algebra and(H,Δ,ε,γ)is a Hom-coalgebra,such that Δ and ε are morphisms of Hom-algebras,i.e.,

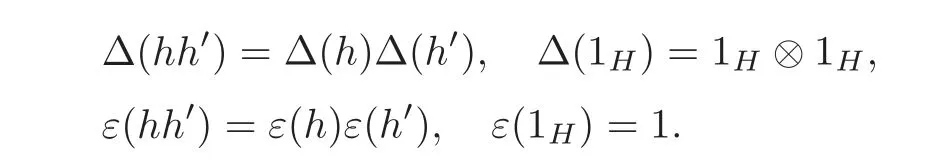
Furthermore,if there exists a linear map S:H −→H such that

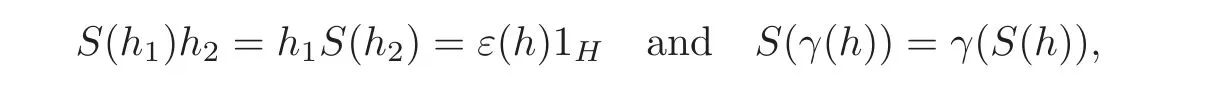
then we call(H,μ,1H,Δ,ε,γ,S)(abbr.(H,γ,S))a Hom-Hopf algebra.

Let(H,γ)and(H?,γ?)be two Hom-bialgebras.The linear map f:H −→ H?is called a Hom-bialgebra map if f◦γ=γ?◦f and at the same time f is a bialgebra map in the usual sense.

Left Hom-module(see[21,25])Let(A,β)be a Hom-algebra.A left(A,β)-Hom-module is a triple(M,?,α),where M is a linear space,?:A⊗M −→ M is a linear map,and α is an automorphism of M,such that

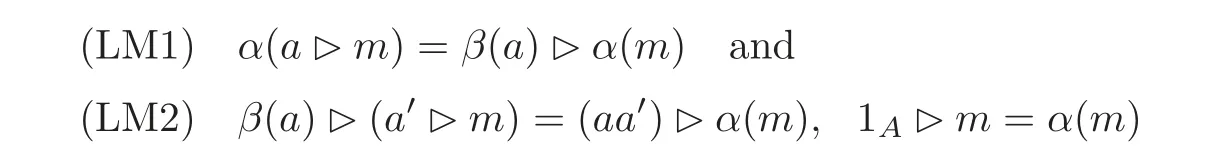
are satisfied for a,a?∈A and m∈M.

Remark 2.1(1)It is obvious that(A,μ,β)is a left(A,β)-Hom-module.

(2)When β =idAand α =idM,a left(A,β)-Hom-module is the usual left A-module.

Right Hom-module(see[13])Let(A,β)be a Hom-algebra.A right(A,β)-Hom-module is a triple(M,?,α),where M is a linear space,?:M ⊗ A −→ M is a linear map,and α is an automorphism of M,such that

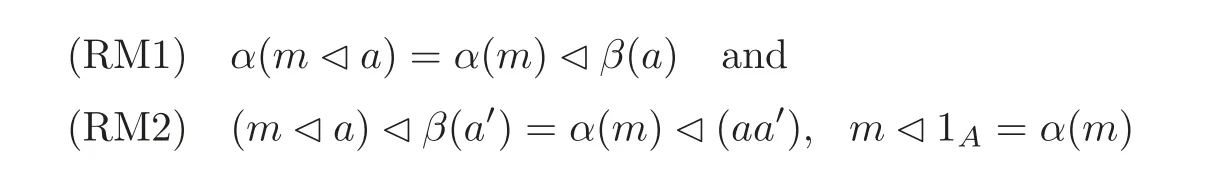
are satisfied for a,a?∈A and m∈M.

Left module Hom-algebra(see[21,25])Let(H,β)be a Hom-bialgebra and(A,α)be a

Hom-algebra.If(A,?,α)is a left(H,β)-Hom-module and for all h ∈ H and a,a?∈ A,

then(A,?,α)is called a left(H,β)-module Hom-algebra.

Remark 2.2(1)When α =idAand β =idH,a left(H,β)-module Hom-algebra is the usual left H-module algebra.

(2)In a way similar to the case of Hopf algebras,in[21,25],Yau concluded that the equation(LMA1)is satisfied if and only if μAis a morphism of H-modules for suitable H-module structures on A⊗A and A,respectively.

Right module Hom-algebra(see[13])Let(H,β)be a Hom-bialgebra and(A,α)be a Hom-algebra.If(A,?,α)is a right(H,β)-Hom-module and for all h ∈ H and a,a?∈ A,

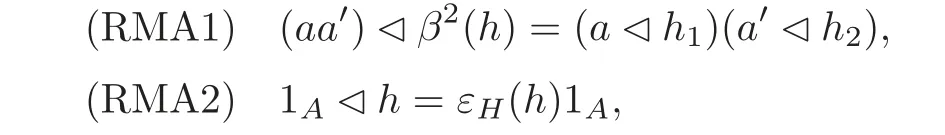
then(A,?,α)is called a right(H,β)-module Hom-algebra.

Left Hom-comodule(see[27]) Let(C,β)be a Hom-coalgebra.A left(C,β)-Homcomodule is a triple(M,ρ,α),where M is a linear space,ρ :M −→ C ⊗ M(write ρ(m)=m(−1)⊗m(0), ∀m ∈ M)is a linear map,and α is an automorphism of M,such that

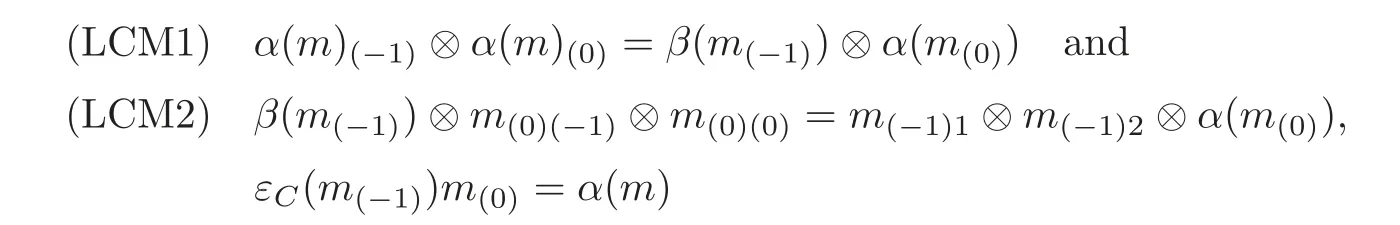
are satisfied for all m∈M.

Remark 2.3(1)It is obvious that(C,ΔC,β)is a left(C,β)-Hom-comodule.

(2)When β =idAand α =idM,a left(C,β)-Hom-comodule is the usual left C-comodule.

Left comodule Hom-coalgebra(see[27])Let(H,β)be a Hom-bialgebra and(C,α)be a Hom-coalgebra.If(C,ρ,α)is a left(H,β)-Hom-comodule and for all c ∈ C,

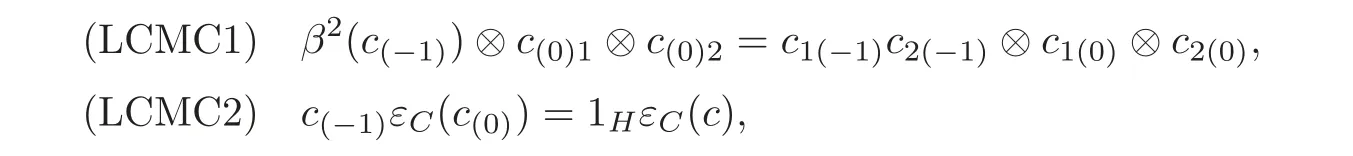
then(C,ρ,α)is called a left(H,β)-comodule Hom-coalgebra.

Remark 2.4(1)It is obvious that(H,ΔH,β)is a left(H,β)-comodule Hom-coalgebra.

(2)When α =idAand β =idH,a left(H,β)-comodule Hom-coalgebra is the usual left H-comodule coalgebra.

(3)In a way similar to the case of Hopf algebras,in[27],Zhang and Li concluded that the equation(LCMC1)is satisfied if and only if ΔCis a morphism of H-comodules for suitable H-comodule structures on C⊗C and C,respectively.

Left module Hom-coalgebra(see[9])Let(H,β)be a Hom-bialgebra and(C,α)be a Hom-coalgebra.If(C,,α)is a left(H,β)-Hom-module and for all h ∈ H and c∈ A,

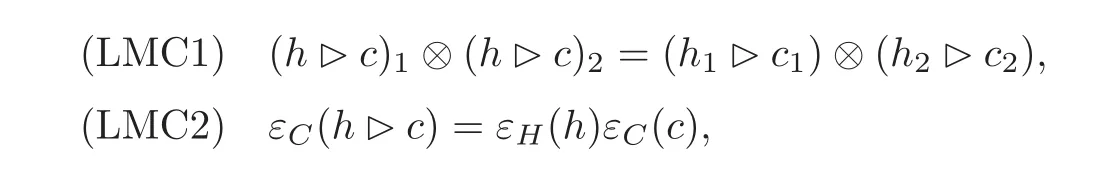
then(C,,α)is called a left(H,β)-module Hom-coalgebra.

Remark 2.5When α =idCand β =idH,a left(H,β)-module Hom-coalgebra is the usual left H-module coalgebra.

Left comodule Hom-algebra(see[22])Let(H,β)be a Hom-bialgebra and(A,α)be a Hom-algebra.If(A,ρ,α)is a left(H,β)-Hom-comodule and for all a,a?∈ A,

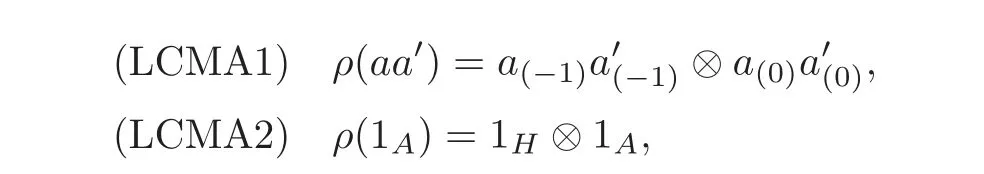
then(A,ρ,α)is called a left(H,β)-comodule Hom-algebra.

Remark 2.6When α =idAand β =idH,a left(H,β)-comodule Hom-algebra is the usual left H-comodule algebra.

Left smash product Hom-algebra(see[6,9])Let(H,β)be a Hom-bialgebra and(A,,α)be a left(H,β)-module Hom-algebra.Then(,α ⊗ β)(=A ⊗ H as a linear space)and unit 1A⊗1His a Hom-algebra with the multiplication

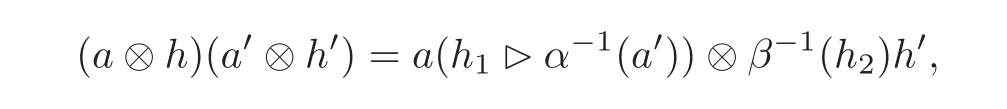
where a,a?∈A,h,h?∈H,and we call it a left smash product Hom-algebra denoted by(,α⊗β).

Remark 2.7(1)Here the multiplication of smash product Hom-algebra is different from that defined by Makhlouf and Panaite in[13,Theorem 3.1].

(2)When α =idAand β =idH,we can get the usual smash product algebra A#H(see[16–17]).

Left smash coproduct Hom-coalgebra(see[6])Let(H,β)be a Hom-bialgebra and(C,ρ,α)be a left(H,β)-comodule Hom-coalgebra.Then(C?H,α ⊗ β)(C?H=C ⊗ H as a linear space)and counit εC⊗ εHis a Hom-coalgebra with the comultiplication

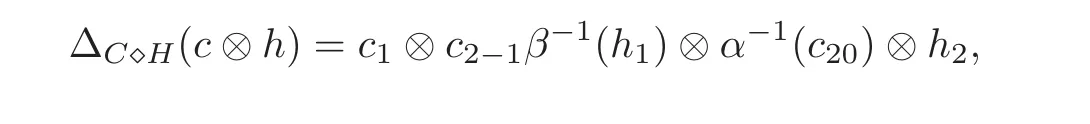
where c∈C,h∈H,and we call it a left smash coproduct Hom-coalgebra denoted by(C?H,α⊗β).

Left Radford biproduct(see[6])Let(H,β)be a Hom-bialgebra,and(A,α)be a left(H,β)-module Hom-algebra with module structure?:H⊗A −→ A and a left(H,β)-comodule Hom-coalgebra with comodule structure ρ:A−→H ⊗A.Then the following are equivalent:

(i)(,,1A⊗ 1H,ΔA?H,εA⊗ εH,α ⊗ β)is a Hom-bialgebra,where A?H is a left smash product Hom-algebra and A?H is a left smash coproduct Hom-coalgebra.

(ii)The following conditions hold(∀a,b∈ A and h ∈ H):

(LR1)(A,ρ,α)is a left(H,β)-comodule Hom-algebra,

(LR2)(A,,α)is a left(H,β)-module Hom-coalgebra,

(LR3)εAis a Hom-algebra map and ΔA(1A)=1A⊗1A,

(LR4)and

(LR5)

Left-left Hom-Yetter-Drinfeld module(see[6])Let(H,β)be a Hom-bialgebra,(M,?M,αM)be a left(H,β)-module with action?M:H ⊗ M −→ M,h ⊗ m?→ h?Mm,and(M,ρM,αM)be a left(H,β)-comodule with coaction ρM:M −→ H ⊗ M,m?→ m(−1)⊗m(0).Then we call(M,?M,ρM,αM)a left-left Hom-Yetter-Drinfeld module over(H,β)if the following condition holds:

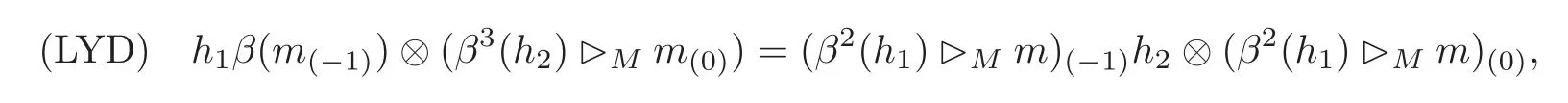
where h∈H and m∈M.

Left-left Hom-Yetter-Drinfeld category(see[6])Let(H,β)be a Hom-bialgebra.Then the left-left Hom-Yetter-Drinfeld categoryis a braided tensor category(see[5]),with tensor product(M ⊗N,αM⊗ αN)and associativity constraints,and the braiding is defined by

and

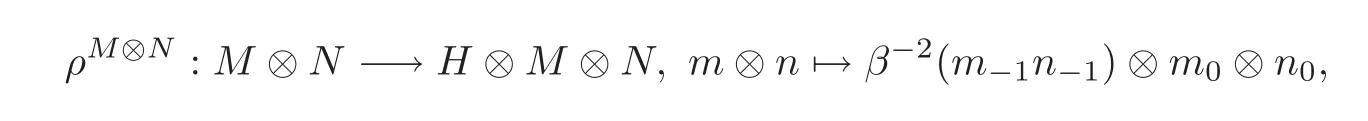
where h∈H,m∈M and n∈N,

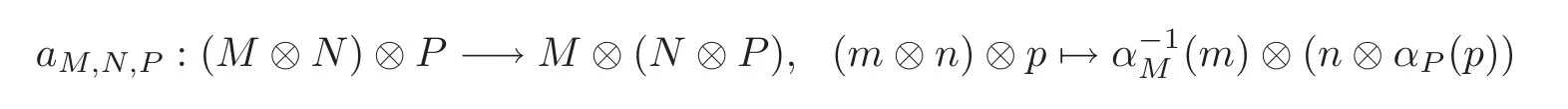
and

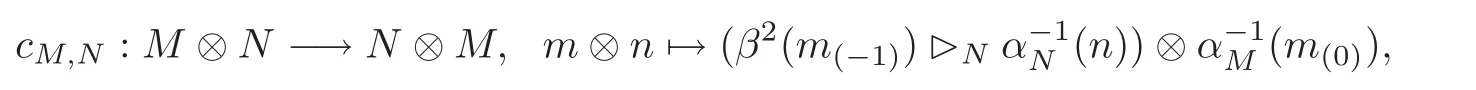
respectively,as well as unit(K,idK).

Left Radford biproduct and left-left Yetter-Drinfeld category(see[6])Let(H,β)be a Hom-bialgebra such that β2=idH,and(A,α)be a left(H,β)-module Hom-algebra and a left(H,β)-comodule Hom-coalgebra.Then,,1A⊗ 1H,,εA⊗ εH,α ⊗ β)is a left Radford biproduct Hom-bialgebra if and only if(A,α)is a Hom-bialgebra in the left-left Hom-Yetter-Drinfeld category

Quasitriangular Hom-Hopf algebra(see[23])A quasitriangular Hom-Hopf algebra is a octuple(H,μ,1H,Δ,ε,S,β,R)(abbr.(H,β,R))in which(H,μ,1H,Δ,ε,S,β)is a Hom-Hopf algebra and R=R1⊗R2∈H⊗H,satisfying the following axioms(for all h∈H and R=r):

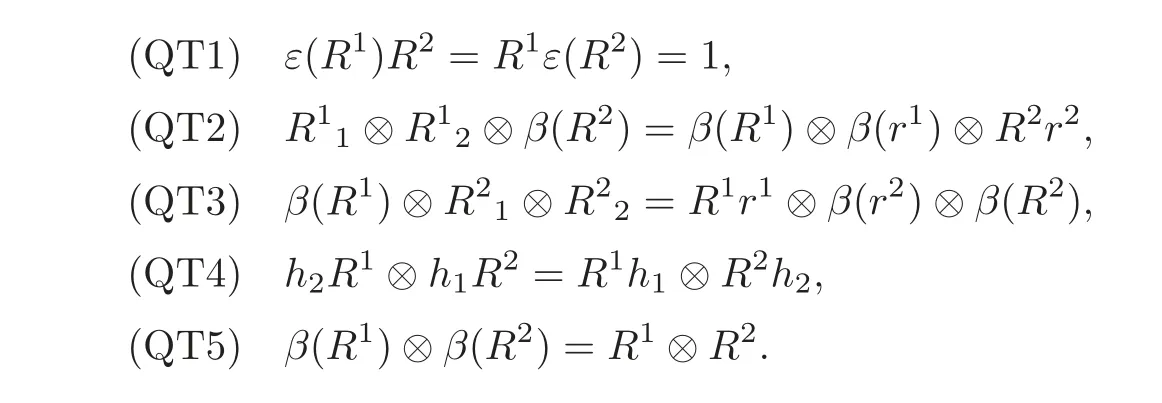
Remark 2.8(1)When α=idH,a quasitriangular Hom-Hopf algebra is exactly the usual quasitriangular Hopf algebra.

(2)It is slightly different from the definition in[23].Here we replace the Hom-bialgebra with the Hom-Hopf algebra and also add another two conditions(QT1)and(QT5).Similar to the Hopf algebra setting,the quasitriangular structure R is invertible.

(3)Based on Yau’s results in[23],each quasitriangular Hom-Hopf algebra comes with solutions of the quantum Hom-Yang-Baxter equations.

3 Double Biproduct Hom-Bialgebra

In this section,we mainly generalize the double biproduct bialgebra to the Hom-setting.In order to define double biproduct Hom-bialgebra,we need first the right-handed versions of some concepts and results.The proofs are similar to the left-handed versions,so we omit them.

definition 3.1Let(C,β)be a Hom-coalgebra.A right(C,β)-Hom-comodule is a triple(M,δ,α),where M is a linear space,δ:M −→ M ⊗C(write δ(m)=m[0]⊗m[1], ∀m ∈ M)is a linear map,and α is an automorphism of M,such that

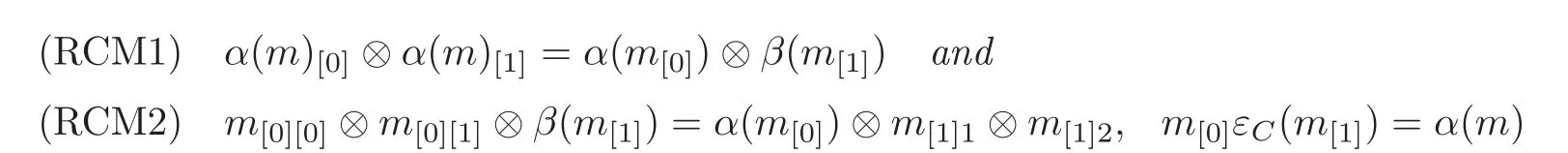
are satisfied for all m∈M.

definition 3.2Let(H,β)be a Hom-bialgebra and(C,α)be a Hom-coalgebra.If(C,δ,α)is a right(H,β)-Hom-comodule and for all c∈ C,

then(C,δ,α)is called a right(H,β)-comodule Hom-coalgebra.

definition 3.3Let(H,β)be a Hom-bialgebra and(C,α)be a Hom-coalgebra.If(C,?,α)is a right(H,β)-Hom-module and for all h ∈ H and c∈ A,

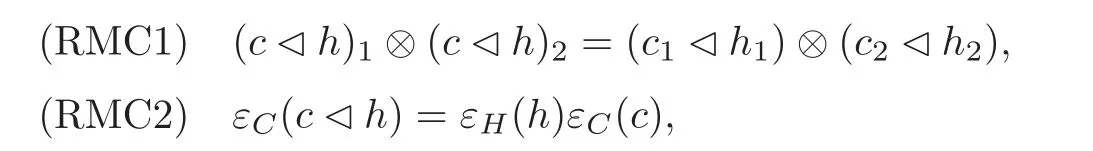
then(C,?,α)is called a right(H,β)-module Hom-coalgebra.

definition 3.4Let(H,β)be a Hom-bialgebra and(A,α)be a Hom-algebra.If(A,δ,α)is a right(H,β)-Hom-comodule and for all a,a?∈ A,

then(A,δ,α)is called a right(H,β)-comodule Hom-algebra.

definition 3.5Let(H,β)be a Hom-bialgebra and(A,,α)be a right(H,β)-module Homalgebra.Then(,β⊗α)(=H⊗A as a linear space)and unit 1H⊗1Ais a Hom-algebra with the multiplication

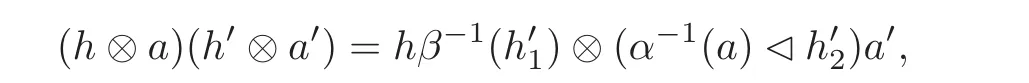
where a,a?∈A,h,h?∈H,and we call it a right smash product Hom-algebra denoted by(,β⊗α).

Proposition 3.1Let(H,β)be a Hom-bialgebra and(C,δ,α)be a right(H,β)-comodule Hom-coalgebra.Then(H?C,β ⊗ α)(H?C=H ⊗ C as a linear space)and counit εH⊗ εCis a Hom-coalgebra with the comultiplication

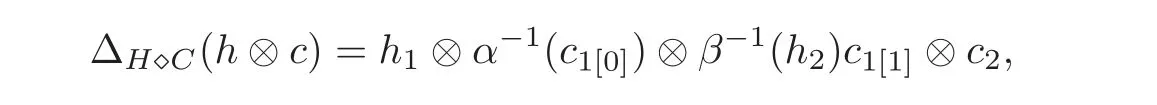
where c∈C,h∈H,and we call it a right smash coproduct Hom-coalgebra denoted by(H?C,β ⊗ α).

Theorem 3.1Let(H,β)be a Hom-bialgebra,and(A,α)be a right(H,β)-module Homalgebra with module structure?:A⊗H −→ A and a right(H,β)-comodule Hom-coalgebra with comodule structure δ:A −→ A⊗H.Then the following are equivalent:

(i)(,μH?A,1H⊗ 1A,ΔH?A,εH⊗ εA,β ⊗ α)is a Hom-bialgebra,where H?A is a right smash product Hom-algebra and H?A is a right smash coproduct Hom-coalgebra.

(ii)The following conditions hold(∀a,b∈ A and h ∈ H):

(RR1)(A,δ,α)is a right(H,β)-comodule Hom-algebra,

(RR2)(A,?,α)is a right(H,β)-module Hom-coalgebra,

(RR3) εAis a Hom-algebra map and ΔA(1A)=1A⊗ 1A,

(RR4)and

(RR5)

definition 3.6Let(H,β)be a Hom-bialgebra,(M,?M,αM)be a right(H,β)-module with action?M:M⊗H −→ M,m⊗h?→ m?Mh and(M,δM,αM)be a right(H,β)-comodule with coaction δM:M −→ M ⊗ H,m?→ m[0]⊗ m[1].Then we call(M,?M,δM,αM)a right-right Hom-Yetter-Drinfeld module over(H,β)if the following condition holds:

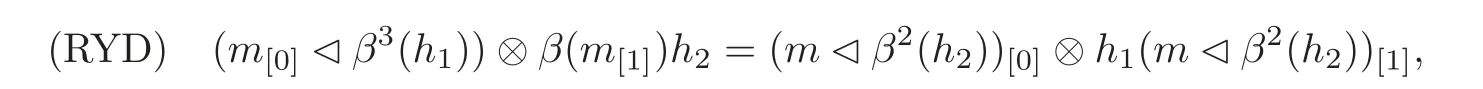
where h∈H and m∈M.

definition 3.7Let(H,β)be a Hom-bialgebra.Then the right-right Hom-Yetter-Drinfeld categoryis a braided tensor category,with tensor product(M ⊗N,αM⊗ αN)and associativity constraints,and the braiding is defined by

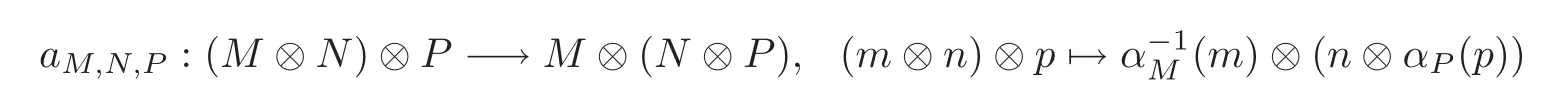
and

respectively,as well as unit(K,idK).

Theorem 3.2Let(H,β)be a Hom-bialgebra such that β2=idH,and(A,α)be a right(H,β)-module Hom-algebra and a right(H,β)-comodule Hom-coalgebra.Then(,μH?A,1H⊗1A,ΔH?A,εH⊗ εA,β ⊗ α)is a right Radford biproduct Hom-bialgebra if and only if(A,α)is a Hom-bialgebra in the right-right Hom-Yetter-Drinfeld category

Next we introduce the two-sided smash product Hom-algebra,the two-sided smash coproduct Hom-coalgebra and the double biproduct Hom-bialgebra.

Proposition 3.2Let(H,β)be a Hom-bialgebra,(A,?,αA)be a left(H,β)-module Homalgebra and(B,?,αB)be a right(H,β)-module Hom-algebra.Then(,αA⊗ β ⊗ αB)(=A⊗H⊗B as a linear space)and unit 1A⊗1H⊗1Bis a Hom-algebra with the multiplication

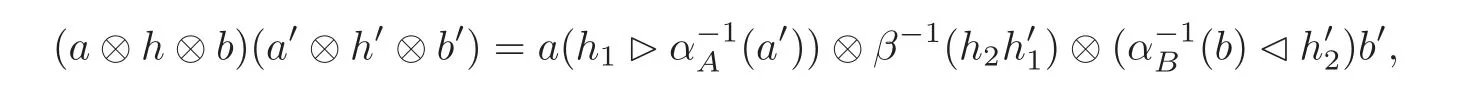
where a,a?∈A,h,h?∈H,b,b?∈B,and we call it a two-sided smash product Hom-algebra denoted by(,αA⊗β⊗αB).

ProofIt is direct to prove that

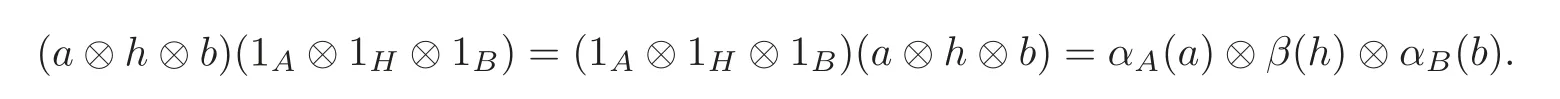
On the other hand,for all a,a?,a??∈A,h,h?,h??∈H and b,b?,b??∈B,we have

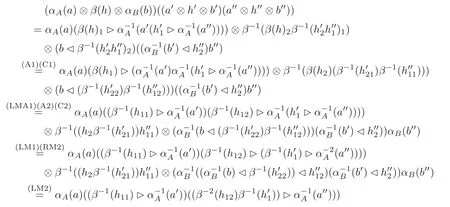
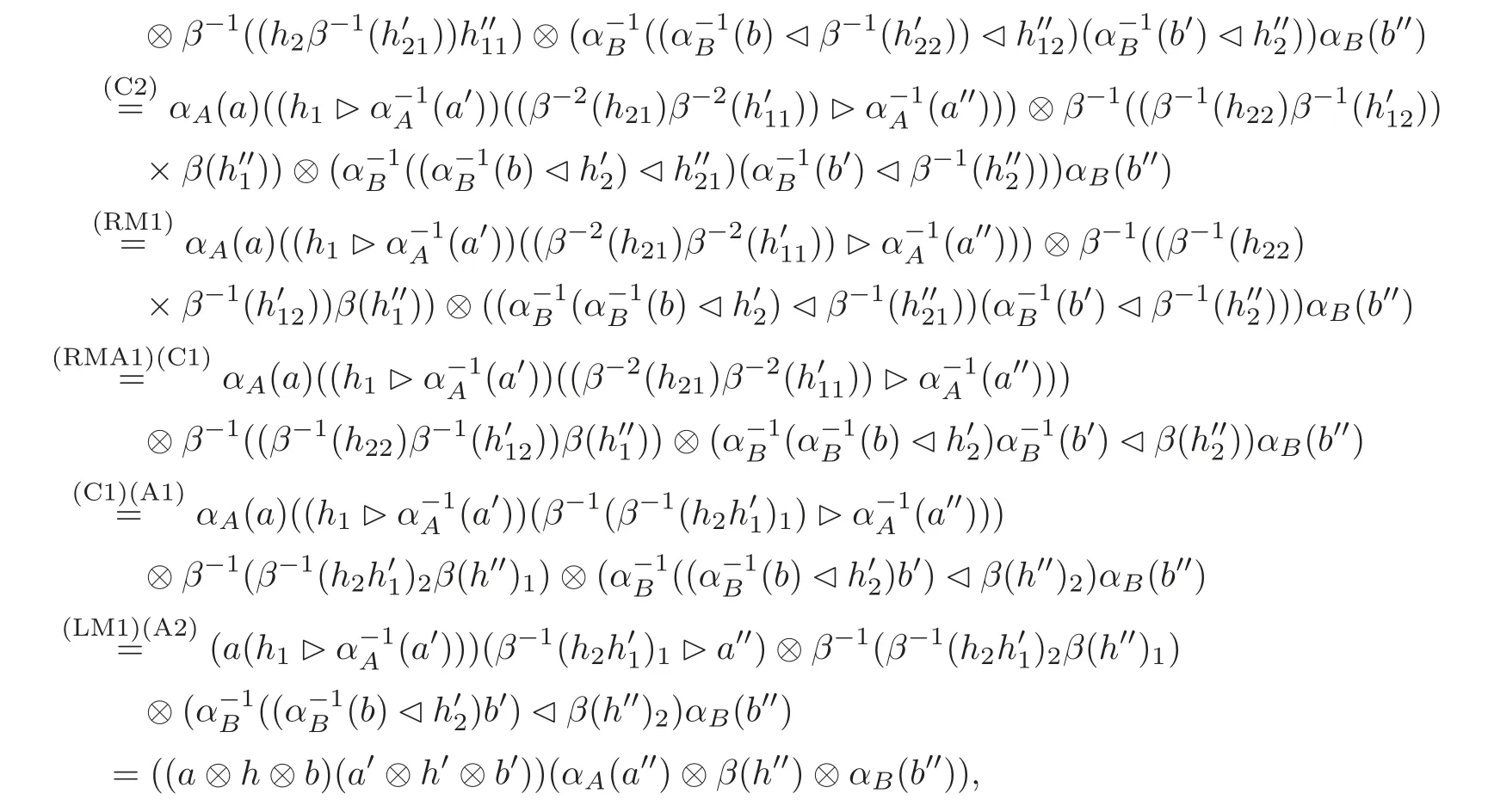
which finishes the proof.

Dually,we have the following proposition.

Proposition 3.3Let(H,β)be a Hom-bialgebra,(A,ρ,αA)be a left(H,β)-comodule Homcoalgebra and(B,δ,αB)be a right(H,β)-comodule Hom-coalgebra.Then(A?H?B,αA⊗β ⊗αB)(A?H?B=A ⊗ H ⊗ B as a linear space)and counit εA⊗ εH⊗ εBis a Hom-coalgebra with comultiplication

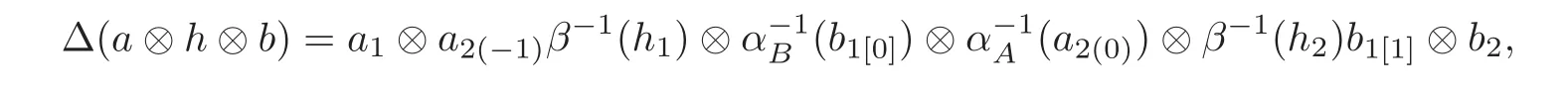
where a∈A,h∈H,b∈B,and we call it a two-sided smash coproduct Hom-coalgebra denoted by(A?H?B,αA⊗β⊗αB).

Theorem 3.3Let(H,β)be a Hom-bialgebra such that β2=idH,(A,αA)be a Hombialgebra in the left-left Hom-Yetter-Drinfeld categoryand(B,αB)be a Hom-bialgebra in the right-right Hom-Yetter-Drinfeld category.Then the two-sided smash product Homalgebra(,αA⊗ β ⊗ αB)equipped with the two-sided smash coproduct Hom-coalgebra(A?H?B,αA⊗β⊗αB)becomes a Hom-bialgebra if and only if

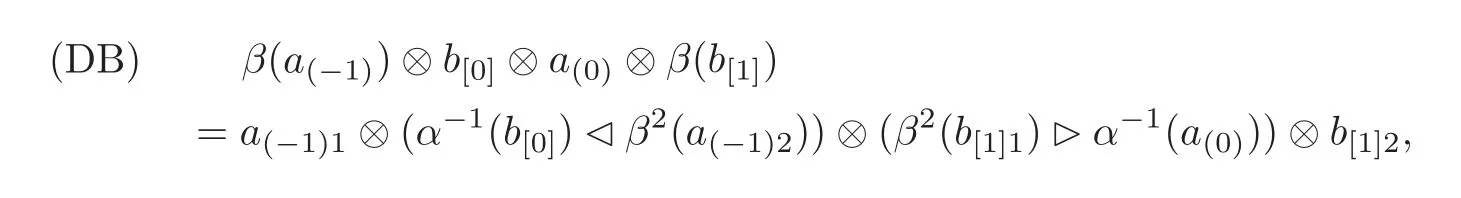
where a∈A and b∈B.

In this case,we call this Hom-bialgebra a double biproduct Hom-bialgebra and denote it by(,αA⊗β⊗αB).

Proof(⇐)We only need to check that ΔA?H?Bis a Hom-algebra map.For all a,a?∈A,h,h?∈H and b,b?∈B,we have

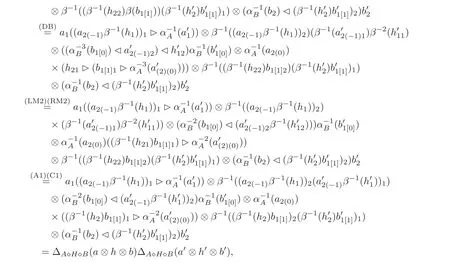
and Δ(1A⊗1H⊗1B)=1A⊗1H⊗1B⊗1A⊗1H⊗1Bis easy.

and we have

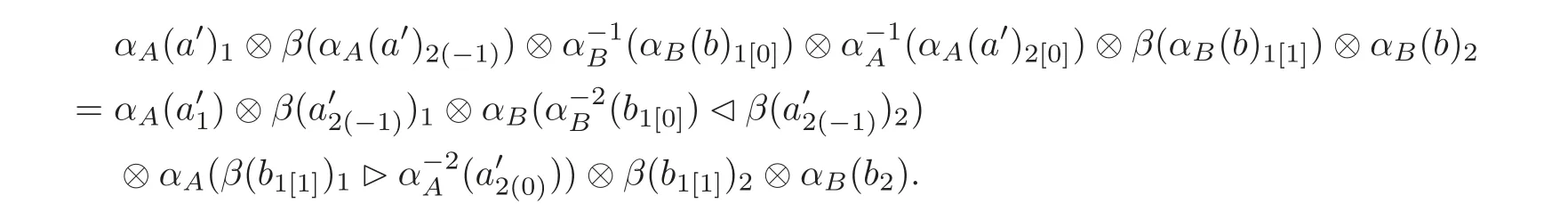
Then,applying εA⊗idH⊗idB⊗idA⊗idH⊗εBto the above equation,by(C1),we obtain the condition(DB).

Remark 3.1(1)When αA=idA, β =idH,and αB=idB,we get Majid’s double biproduct bialgebra in[11].

(2)Let B=K,and we obtain the left Radford’s biproduct Hom-bialgebra.Let A=K,and we obtain the following right Radford’s biproduct Hom-bialgebra

Corollary 3.1Let(H,β)be a Hom-bialgebra,and(A,α)be a right(H,β)-module Homalgebra with module structure?:A⊗H −→ A and a right(H,β)-comodule Hom-coalgebra with comodule structure δ:A −→ A⊗H.Then the following are equivalent:

(i)is a Hom-bialgebra,where H?A is a right smash product Hom-algebra and H?A is a right smash coproduct Hom-coalgebra.

(ii)The following conditions hold(∀a,b∈ A and h ∈ H):

(RR1)(A,δ,α)is a right(H,β)-comodule Hom-algebra,

(RR2)(A,?,α)is a right(H,β)-module Hom-coalgebra,

(RR3) εAis a Hom-algebra map and ΔA(1A)=1A⊗ 1A,

(RR4)and

(RR5)

Also,we have the following corollary.

Corollary 3.2Let(H,β)be a Hom-bialgebra such that β2=idH,and(A,α)be a right(H,β)-module Hom-algebra and a right(H,β)-comodule Hom-coalgebra.Then1A,ΔH?A,εH⊗ εA,β ⊗ α)is a right Radford biproduct Hom-bialgebra if and only if(A,α)is a Hom-bialgebra in the right-right Hom-Yetter-Drinfeld category

4 Quasitriangular Smash Coproduct Hom-Hopf Algebras

In this section,we introduce a class of new Hom-Hopf algebras:The T-smash coproduct C?TH,generalizing the T-smash coproduct studied in[3,14].The Hom-smash coproduct Hom-Hopf algebra is a special case.Necessary and sufficient conditions for the smash coproduct Hom-Hopf algebra to be quasitriangular are given.

In a way dual to[9,Theorem 3.1],we have the following proposition.

Proposition 4.1Let(C,ΔC,εC,α)and(H,ΔH,εH,β)be two Hom-coalgebras,and T:C⊗H −→H⊗C(write T(c⊗h)=hT⊗cT,∀c∈C,h∈H)be a linear map such that for all c∈C and h∈H,

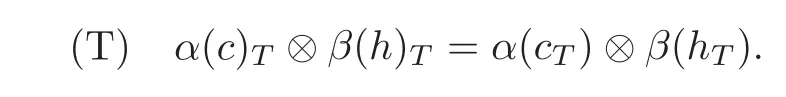
Then(C?TH,α ⊗ β)(C?TH=C ⊗ H as a linear space)and counit εC⊗ εHwith the comultiplication

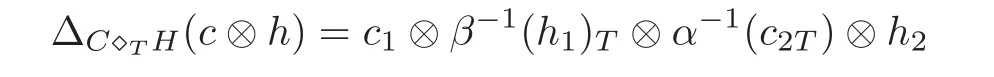
becomes a Hom-coalgebra if and only if the following conditions hold:

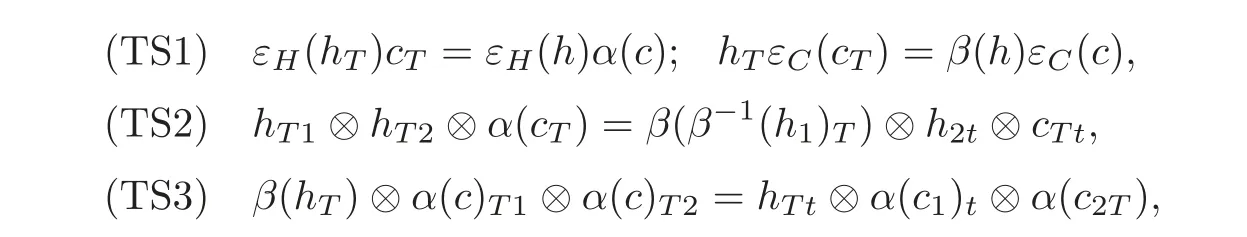
where c∈C,h∈H and t is a copy of T.

We call this a Hom-coalgebra T-smash coproduct Hom-coalgebra and denote it by(C?TH,α⊗β).

Remark 4.1(1)Let T(c⊗h)=c−1h⊗c0in C?TH,and we can get the smash coproduct Hom-coalgebra C?H.

(2)When α =idCand β =idH,we can get the usual T-smash coproduct coalgebra(see[3,10]).

Theorem 4.1Let(C,α,SC)and(H,β,SH)be two Hom-Hopf algebras,and T:C⊗H −→H⊗C be a linear map.Then the T-smash coproduct Hom-coalgebra(C?TH,α⊗β)equipped with the tensor product Hom-algebra structure becomes a Hom-bialgebra if and only if T is a Hom-algebra map.Furthermore,the T-smash coproduct Hom-bialgebra(C?TH,α ⊗ β)is a Ho

m-Hopf algebra with antipodedefined by

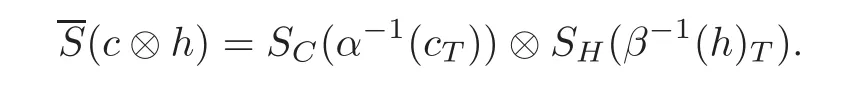
ProofWe only prove thatis an antipode of(C?TH,α⊗β).The rest is straightforward by direct computation.For all c∈C and h∈H,

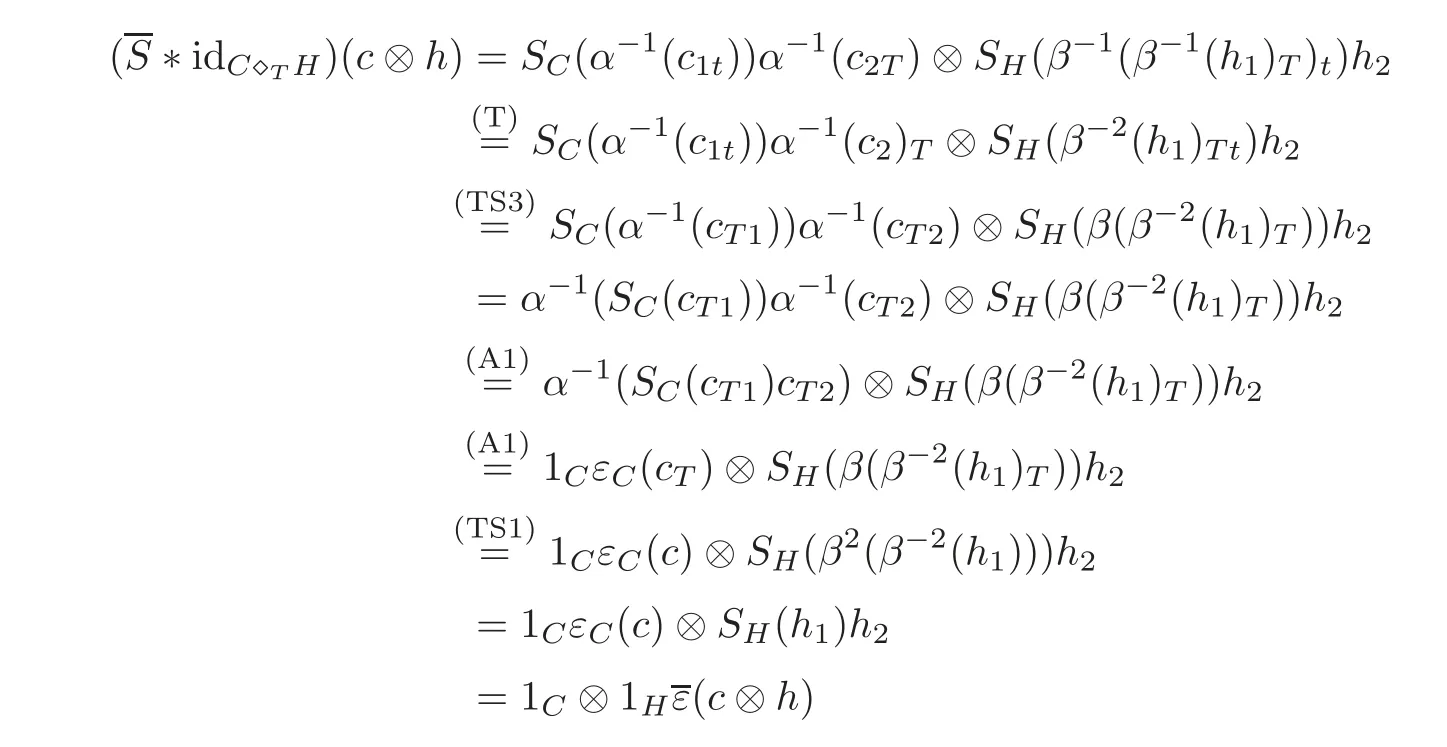
and

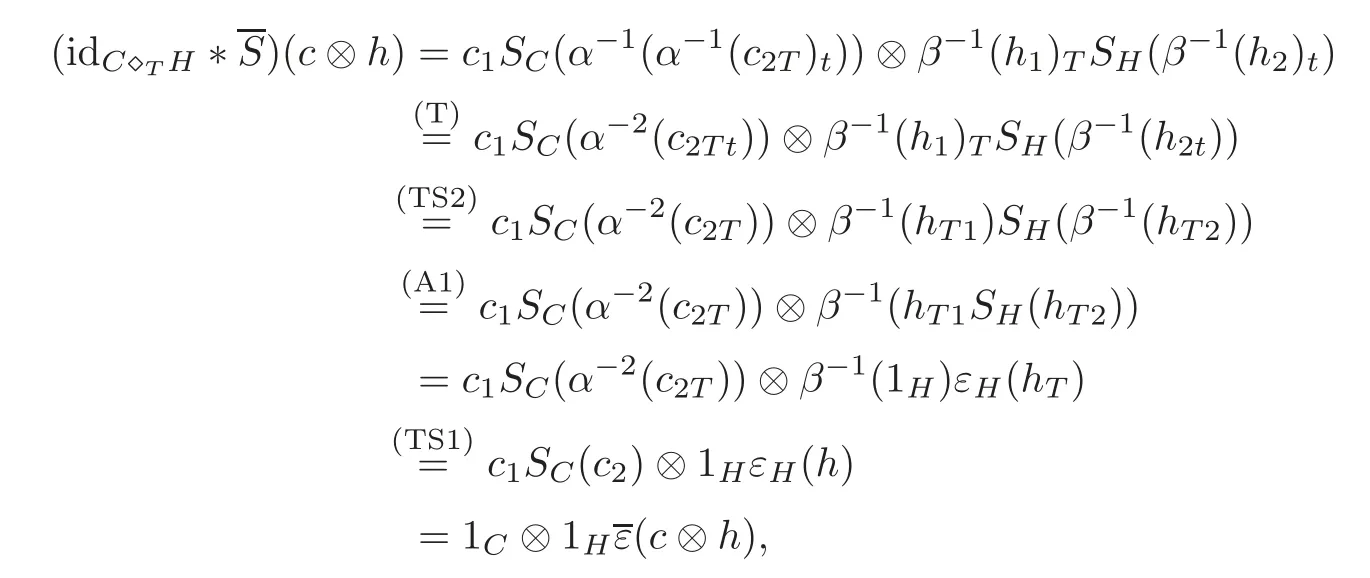
while

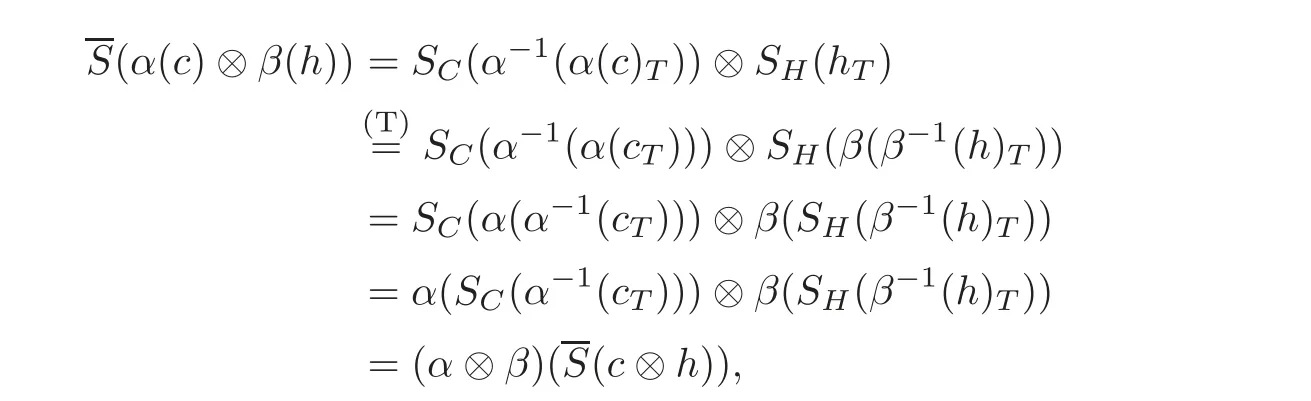
which finishes the proof.

Theorem 4.2Let(C,α,SC)and(H,β,SH)be two Hom-Hopf algebras,and(C,ρ,α)be a left(H,β)-comodule Hom-coalgebra.Then the smash coproduct Hom-coalgebra(C?H,α ⊗ β)endowed with the tensor product Hom-algebra structure becomes a Hom-bialgebra if and only if(C,ρ,α)is a left(H,β)-comodule Hom-algebra and the following condition holds:

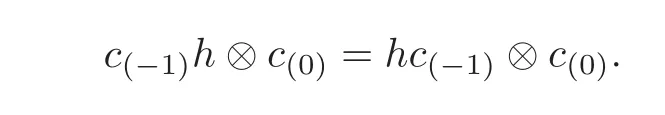
Moreover,the smash coproduct Hom-bialgebra(C?H,α ⊗ β)is a Hom-Hopf algebra with the antipode

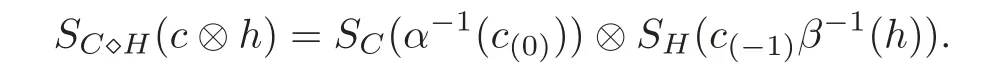
ProofLet T(c⊗h)=c(−1)h⊗c(0),∀c∈ C,h∈ H in Theorem 4.1.

Next,we generalize the concept of compatibility Hopf algebra pairs(see[10])to the Homsetting.

definition 4.1Let(C,α,SC)and(H,β,SH)be two Hom-Hopf algebras,and ϑ = ϑ1⊗ϑ2∈C ⊗H.A Hom-compatibility Hopf algebra triple is a triple(C,H,ϑ)such that(ϑ = ϑ)

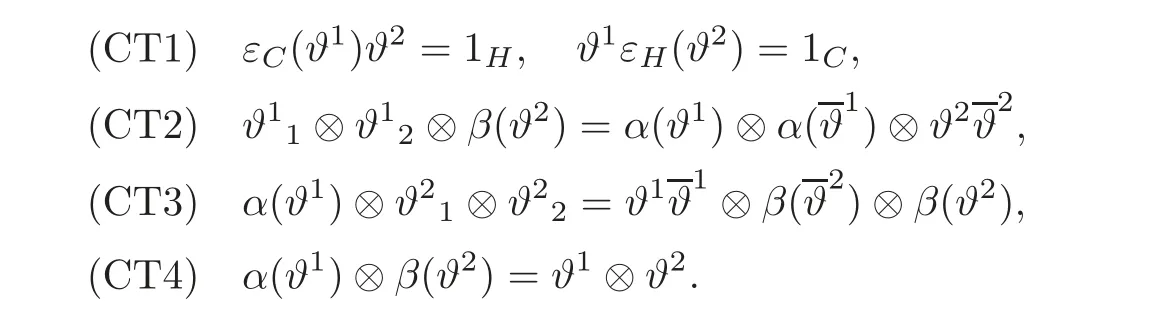
Remark 4.2(1)When α =idCand β =idH,we can get the compatibility Hopf algebra pairs.

(2)If(H,β,R)is a quasitriangularHom-Hopf algebra,then(H,H,R)is a Hom-compatibility Hopf algebra triple.

(3) ϑ is(convolution)invertible with ϑ−1=SC(ϑ1)⊗ ϑ2.

Proposition 4.2Let(C?TH,α⊗β)be a T-smash coproduct Hom-Hopf algebra.define

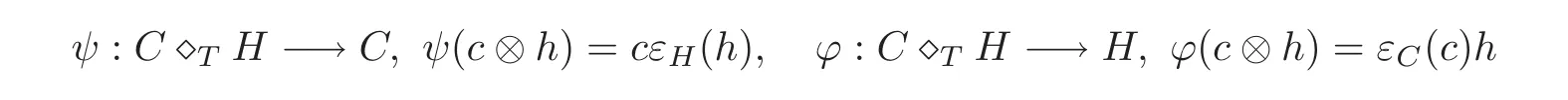
for all c ∈ C and h ∈ H.Then ψ and ϕ are both Hom-bialgebra maps.

ProofStraightforward.

Let(C?TH,α⊗β)be a T-smash coproduct Hom-Hopf algebra,and R∈C?TH⊗C?TH.define

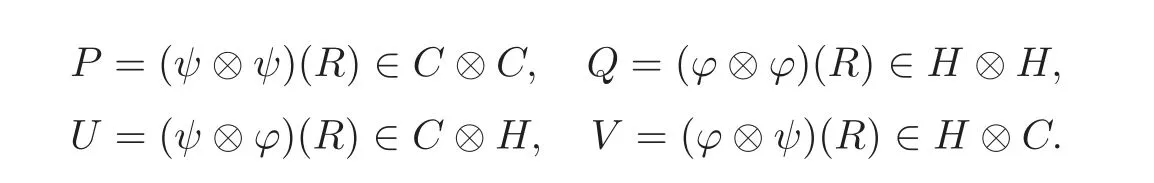
The following two lemmas are obvious.

Lemma 4.1Let(C?TH,α⊗β)be a T-smash coproduct Hom-Hopf algebra.If R satisfies(QT1),then

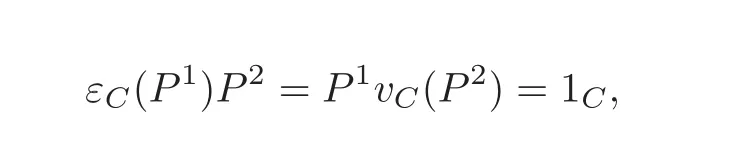
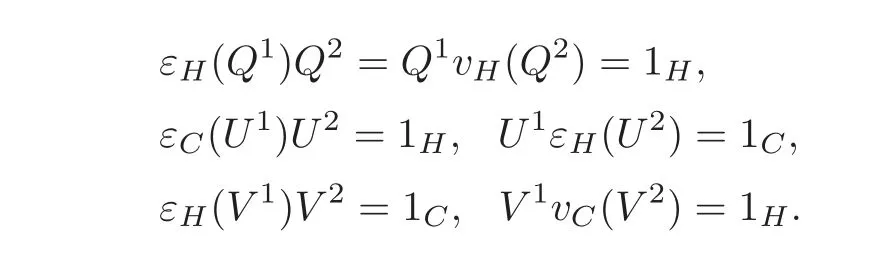
Lemma 4.2Let(C?TH,α⊗β)be a T-smash coproduct Hom-Hopf algebra.If R satisfies(QT5)for α ⊗ β,then

Lemma 4.3Let(C?TH,α ⊗ β,R)be a quasitriangular T-smash coproduct Hom-Hopf algebra.Then,we have

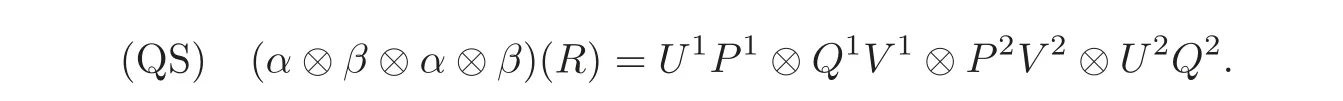
ProofBy(QT2)and(QT3),we have

Applying ψ⊗ϕ⊗ψ⊗ϕ to the above equation,we can get(QS).

Lemma 4.4Let(C?TH,α ⊗ β,R)be a quasitriangular T-smash coproduct Hom-Hopf algebra.Then,for all c∈C,and h∈H,we have

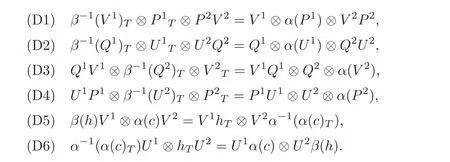
ProofBy(QT2),we can obtain

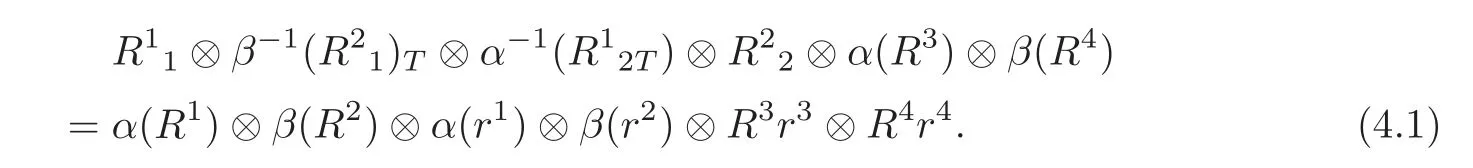
Applying ϕ⊗ψ⊗ψ to(4.1),we have that(D1)holds by(QS)and(T).Similarly,applying ϕ⊗ψ⊗ϕ to(4.1),we can get(D2)by(QS)and(T).

By(QT3),we have

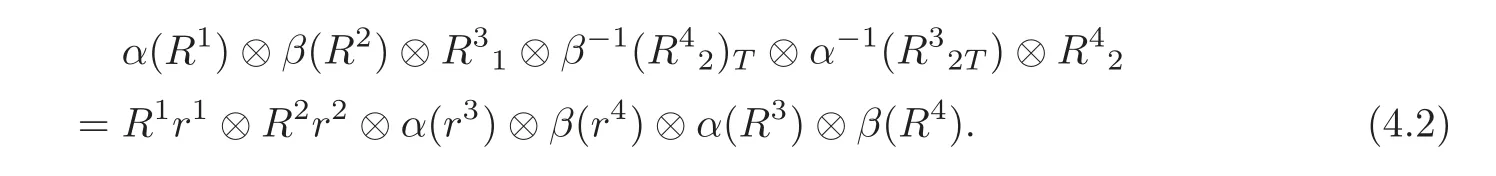
(D3)can be obtained by applying ϕ⊗ϕ⊗ψ to(4.2)and by(QS)and(T).Likewise,one gets(D4)by using ψ⊗ϕ⊗ψ to(4.2)and by(QS)and(T).

By(QT4),for all c∈C and h∈H,we have

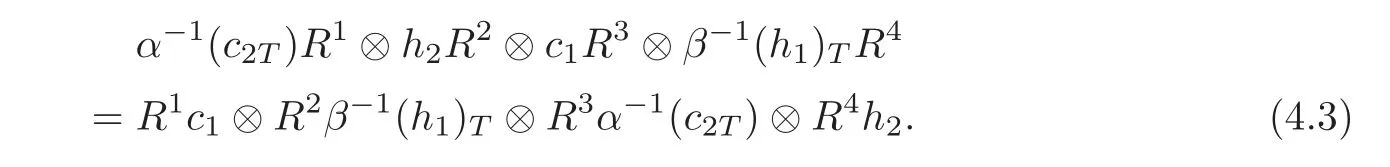
Apply ϕ ⊗ ψ to(4.3),we get(D5).(D6)is derived by applying ψ ⊗ ϕ to(4.3).

Lemma 4.5Given a quasitriangular structure R on a T-smash coproduct Hom-Hopf algebra(C?TH,α⊗β),consider the induced elements P,Q,U and V.Then

(1)(C,α,P)and(H,β,Q)are quasitriangular Hom-Hopf algebras,and

(2)(C,H,U)and(H,C,V)are Hom-compatibility Hopf algebra triples.

Proof(1)Applying ϕ⊗ϕ⊗ϕ to(4.1)and(4.2),we can get(QT2)and(QT3)for P,respectively.(QT4)can be derived by applying ϕ ⊗ ϕ to(4.3).Then by Lemmas 4.1–4.2,(C,α,P)is a quasitriangular Hom-Hopf algebra.Similarly,we can prove that(H,β,Q)is a quasitriangular Hom-Hopf algebra.

(2)Apply ψ⊗ψ⊗ϕ to(4.1),and ψ⊗ϕ⊗ϕ to(4.2).(CT2)and(CT3)can be obtained for U,respectively.Then(C,H,U)is a Hom-compatibility Hopf algebra triple by Lemmas 4.1–4.2.The rest of(4.2)can be similarly demonstrated.

Lemma 4.6Let(C?TH,α⊗β)be a T-smash coproduct Hom-Hopf algebra.If there exist elements P∈C⊗C,Q∈H⊗H,U∈C⊗H and V∈H⊗C such that

(1)(C,α,P)and(H,β,Q)are quasitriangular Hom-Hopf algebras,

(2)(C,H,U)and(H,C,V)are Hom-compatibility Hopf algebra triples,and

(3)the conditions(D1)–(D6)in Lemma 4.4 hold,

then(C?TH,α⊗β,R)is a quasitriangular Hom-Hopf algebra with the quasitriangular structure given by

ProofIt is obvious that R satisfies(QT1)and(QT5).

Next,we show that(QT3)holds for R:

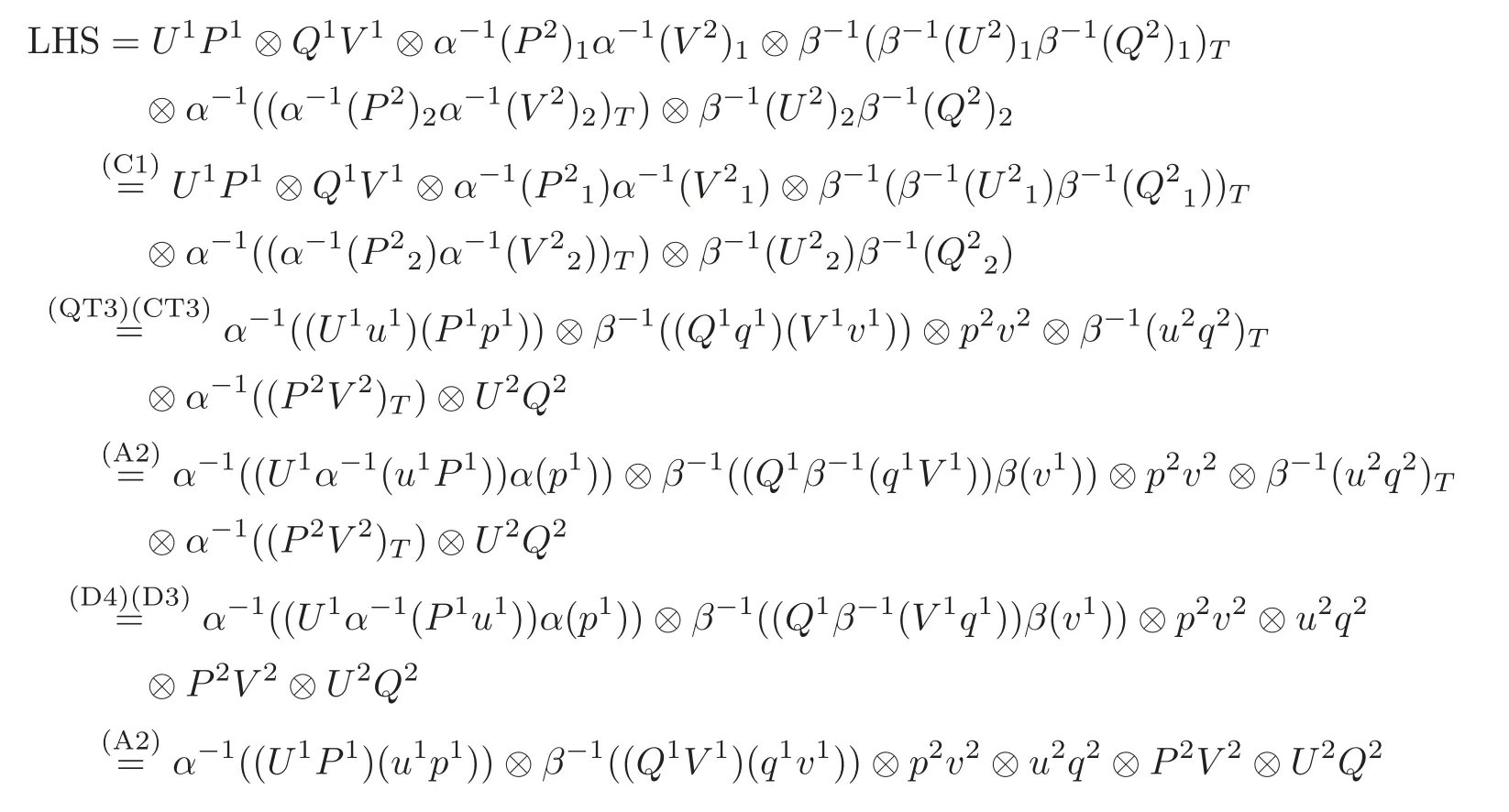
(QT2)for R can be proved by the similar method.And we check(QT4)as follows:

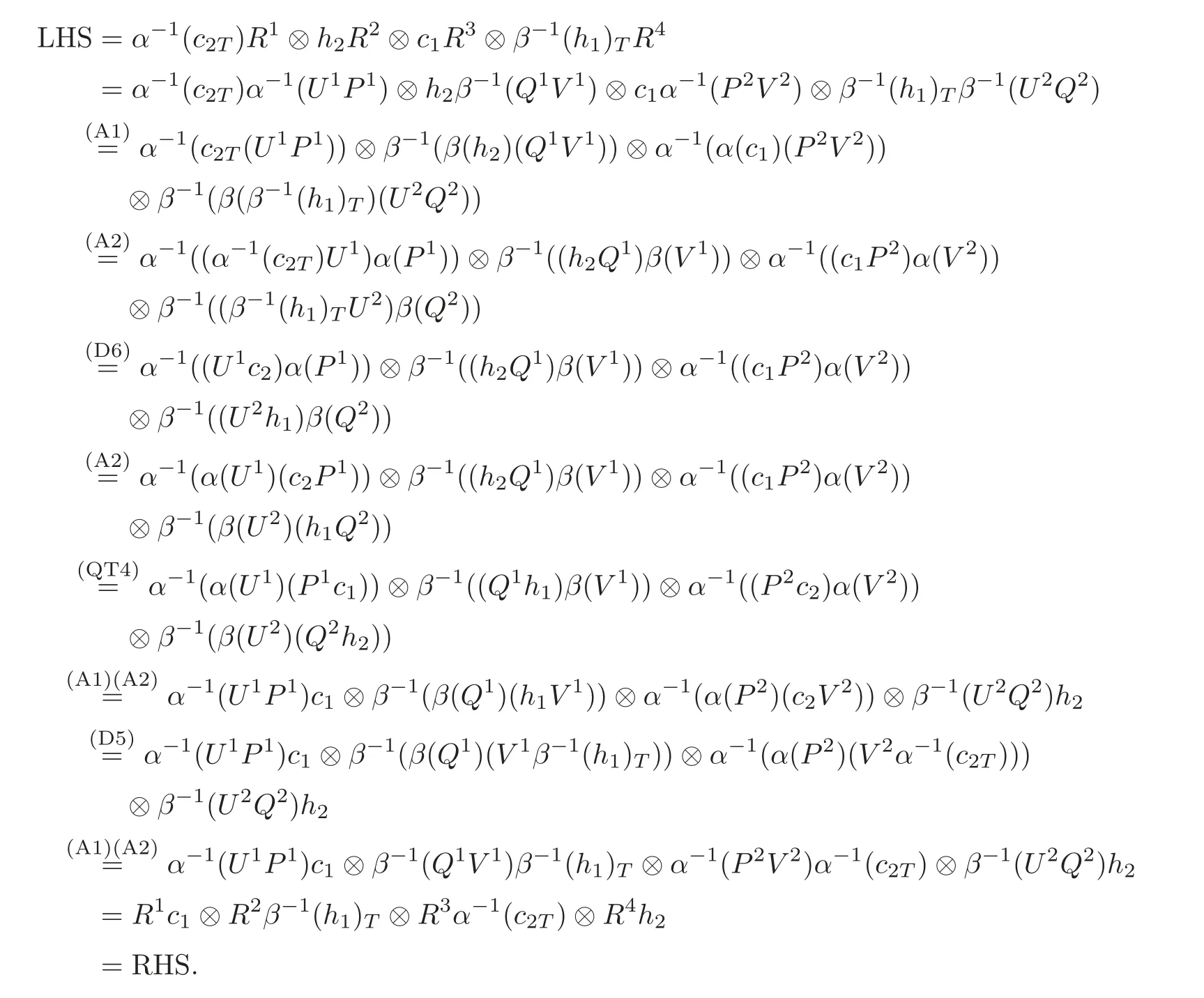
Therefore,(C?TH,α⊗β,R)is a quasitriangular Hom-Hopf algebra.

Thus it follows from Lemmas 4.1–4.6 that we have the following theorems.

Theorem 4.3The T-smash coproduct Hom-Hopf algebra(C?TH,α⊗β)is quasitriangular if and only if there exist elements P∈C⊗C,Q∈H⊗H,U∈C⊗H and V∈H⊗C such that(C,α,P)and(H,β,Q)are quasitriangular Hom-Hopf algebras,(C,H,U)and(H,C,V)are Hom-compatibility Hopf algebra triples,and the conditions(D1)–(D6)in Lemma 4.4 hold.Moreover,the quasitriangular structure R on(CTH,α⊗β)has a decomposition

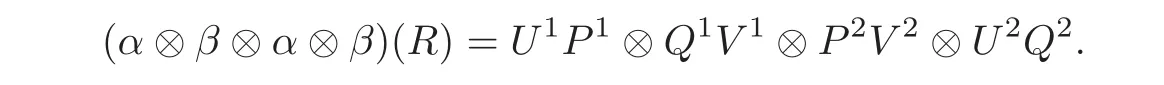
Theorem 4.4The smash coproduct Hom-Hopf algebra(C?H,α ⊗ β)is quasitriangular if and only if there exist elements P∈C⊗C,Q∈H⊗H,U∈C⊗H and V∈H⊗C such that(C,α,P)and(H,β,Q)are quasitriangular Hom-Hopf algebras,(C,H,U)and(H,C,V)are Hom-compatibility Hopf algebra triples,and the conditions(E1)–(E6)below hold:

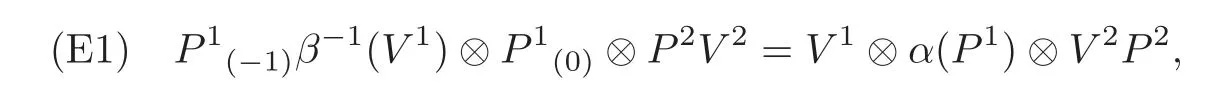
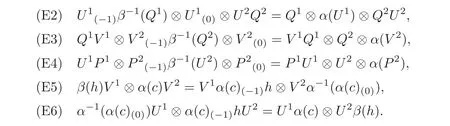
Moreover,the quasitriangular structure R on(CH,α⊗β)has a decomposition

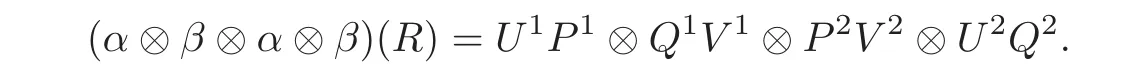
ProofLet T(c⊗h)=c(−1)h⊗c(0),∀a∈A,h∈H in Theorem 4.3.

5 Applications

In this section,we extend the applications of the main results in Section 4 to a concrete example.

The following result is clear.

Lemma 5.1Let KZ2=K{1,a}be a Hopf group algebra(see[19]).Then(KZ2,idKZ2,Q)is a quasitriangular Hom-Hopf algebra,where Q=(1⊗1+a⊗1+1⊗a−a⊗a).

Let T2,−1=K{1,g,x,gx|g2=1,x2=0,xg= −gx}be Taft’s Hopf algebra(see[20]),and its coalgebra structure and antipode are given by

and

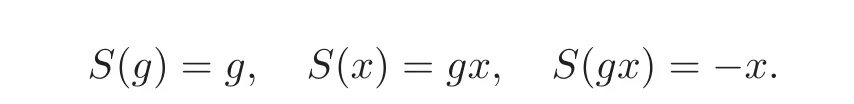
define a linear map α:T2,−1−→ T2,−1by

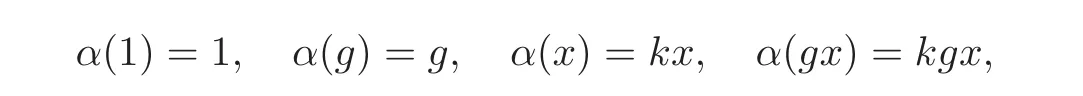
where 0k ∈ K.Then α is an automorphism of Hopf algebras.

So we can get a Hom-Hopf algebra(see[15]).

Lemma 5.2Let Hαbe the Hom-Hopf algebra defined as above.Then(Hα,α,P)is a quasitriangular Hom-Hopf algebra,where P=1⊗1+g⊗1+1⊗g−g⊗g).

ProofIt is straightforward by a tedious computation.

Theorem 5.1Let KZ2be the Hopf group algebra and Hαbe the Hom-Hopf algebra defined as above.define the comodule action ρ:Hα−→ KZ2⊗Hαby

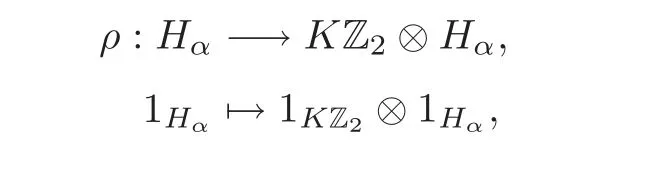
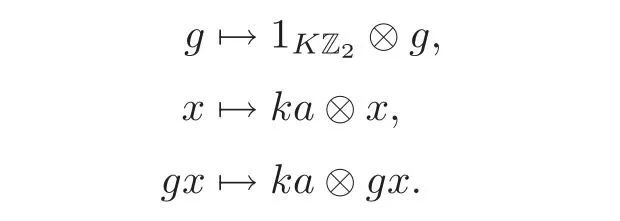
Then by a routine computation we can get that(Hα,ρ,α)is a left KZ2-comodule Hom-coalgebra.Therefore,(,α⊗idKZ2)is a smash coproduct Hom-coalgebra.

Furthermore,(,α ⊗idKZ2)with the tensor product Hom-algebra becomes a Hom-Hopf algebra,where the antipodeis given by

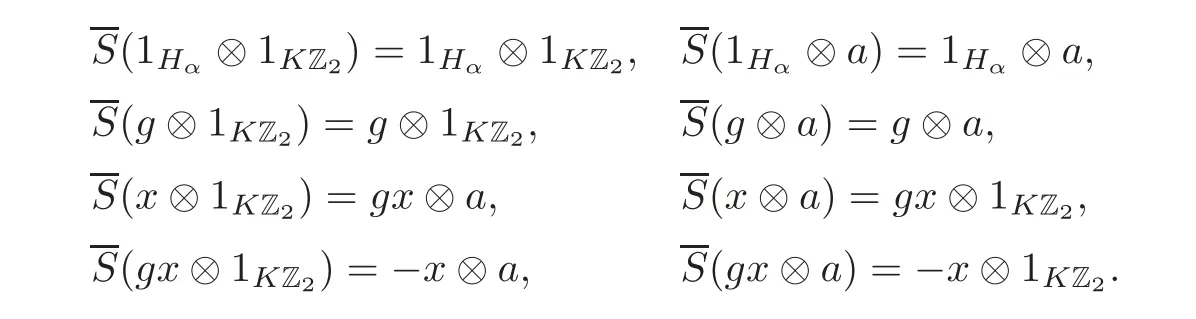
Lemma 5.3Let KZ2be the Hopf group algebra and Hαbe the Hom-Hopf algebra defined as above.define

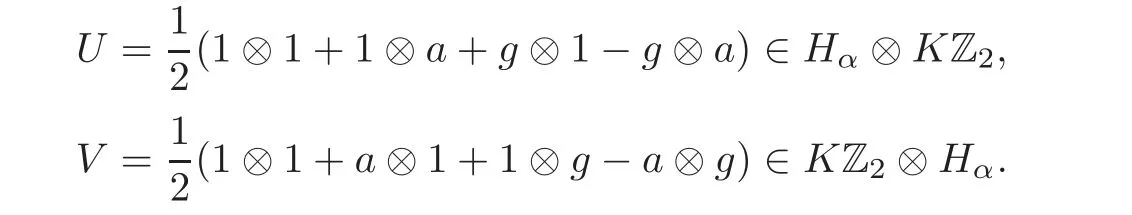
Then(Hα,KZ2,U)and(KZ2,Hα,V)are two Hom-compatibility Hopf algebra triples.

ProofStraightforward.

Theorem 5.2With the notations as above,the smash coproduct Hom-Hopf algebra

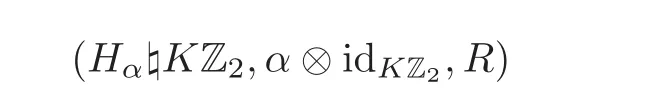
is a quasitriangular Hom-Hopf algebra,where

ProofIt is easy to prove that the conditions(E1)–(E6)hold.And by Lemmas 5.1–5.3 and Theorem 4.4,we can finish the proof.

AcknowledgementThe authors are deeply indebted to the reviewers for their very useful suggestions and some improvements on the original manuscript.

[1]Andruskiewitsch,N.and Schneider,H.-J.,On the classification of finite-dimensional pointed Hopf algebras,Ann.Math.,171(1),2010,375-417.

[2]Caenepeel,S.and Goyvaerts,I.,Monoidal Hom-Hopf algebras,Comm.Algebra,39(6),2011,2216–2240.

[3]Caenepeel,S.,Ion,B.,Militaru,G.and Zhu,S.L.,The factorization problem and the smash biproduct of algebras and coalgebras,Algebra Represent.Theory,3,2000,19–42.

[4]Hu,N.,q-Witt algebras,q-Lie algebras,q-holomorph structure and representations,Algebra Colloq.,6(1),1999,51–70.

[5]Kassel,C.,Quantum Groups,Graduate Texts in Mathematics,155,Springer-Verlag,Berlin,1995.

[6]Li,H.Y.and Ma,T.S.,A construction of Hom-Yetter-Drinfeld category,Colloq.Math.,137(1),2014,43–65.

[7]Ma,T.S.,Jiao,Z.M.and Song,Y.N.,On crossed double biproduct,J.Algebra Appl.,12(5),2013,1250211,17 pages.

[8]Ma,T.S.and Li,H.Y.,On Radford biproduct,Comm.Algebra,43(9),2015,3946–3966.

[9]Ma,T.S.,Li,H.Y.and Yang,T.,Cobraided smash product Hom-Hopf algebras,Colloq.Math.,134(1),2014,75–92.

[10]Ma,T.S.and Wang,S.H.,Bitwistor and quasitriangular structures of bialgebras,Comm.Algebra,38(9),2010,3206–3242.

[11]Majid,S.,Double-bosonization of braided groups and the construction of Uq(g),Math.Proc.Cambridge Philos.Soc.,125(1),1999,151–192.

[12]Makhlouf,A.and Panaite,F.,Yetter-Drinfeld modules for Hom-bialgebras,J.Math.Phys.,55,2014,013501.

[13]Makhlouf,A.and Panaite,F.,Twisting operators,twisted tensor products and smash products for Homassociative algebras,Glasgow Math.J.,58,2016,513–538.

[14]Makhlouf,A.and Silvestrov,S.D.,Hom-algebra stuctures,J.Gen.Lie Theory Appl.,2,2008,51–64.

[15]Makhlouf,A.and Silvestrov,S.D.,Hom-algebras and hom-coalgebras,J.Algebra Appl.,9,2010,553–589.

[16]Molnar,R.K.,Semi-direct products of Hopf algebras,J.Algebra,47,1977,29–51.

[17]Radford,D.E.,The structure of Hopf algebra with a projection,J.Algebra,92,1985,322–347.

[18]Radford,D.E.,Biproducts and Kashina’s examples,Comm.Algebra,44(1),2014,174–204.

[19]Sweedler,M.E.,Hopf Algebras,Benjamin,New York,1969.

[20]Taft,E.J.,The order of the antipode of finite dimensional Hopf algebra,Proc.Nat.Acad.Sci.USA,68,1971,2631–2633.

[21]Yau,D.,Module Hom-algebras.arXiv:0812.4695v1

[22]Yau,D.,Hom-bialgebras and comodule Hom-algebras,Int.Electron.J.Algebra,8,2010,45–64.

[23]Yau,D.,Hom-quantum groups I,quasitriangular Hom-bialgebras,J.Phys.A,45(6),2012,065203,23 pages.

[24]Yau,D.,Hom-quantum groups II,cobraided Hom-bialgebras and Hom-quantum geometry.arXiv:0907.1880

[25]Yau,D.,Hom-quantum groups III,representations and module Hom-algebras.arXiv:0911.5402

[26]Yau,D.,The Hom-Yang-Baxter equation and Hom-Lie algebras,J.Math.Phys.,52,2011,053502.

[27]Zhang,T.and Li,J.,Comodule Hom-coalgebras,Int.J.Algebra and Statistics,2(1),2013,57–63.