IRT理论不同模型下同时校准等值方法的跨样本研究
2016-06-05张泉慧黄慧英
张泉慧 黄慧英
IRT理论不同模型下同时校准等值方法的跨样本研究
张泉慧 黄慧英
本研究基于IRT理论中最常用的LOGISTIC三种模型来探讨等值的跨样本一致性,研究对象为某一汉语类别的测验,等值方法采用同时校准法。研究结果表明,双参数模型下同时校准法等值跨样本一致性最好,最为稳定。
IRT;LOGISTIC模型;同时校准法;跨样本一致性
等值是心理与教育测量的重要概念,其是指将同一测验不同版本的分数统一在一个量表上的过程,从而实现了不同时间、地点、考生的分数可比性,保证了测验公平有效。
跨样本一致性是等值的一个性质。跨样本一致性是指基于总体得到的等值系数与基于不同样本得到的等值系数是不变的(Dorans&Holland,2000),即测验等值应独立于等值程序所使用的样本及数据,根据不同样本建立起来的两测验间的等值关系应基本一致。
但在实际操作中,等值或多或少都存在样本的依赖性(Holland&Rubin,1982)。国内外目前进行的等值都是基于跨样本一致的假设之上,国外对于这一研究已有近60年的历史,做了大量实证性的检验工作;相比之下,国内考试业虽然日益重视等值,但对跨样本一致性的研究还很少,对项目反映理论(IRT)下的跨样本一致性研究更少。因此,本研究即针对IRT理论中三种LOGISTIC模型进行跨样本一致性的研究,采用最为广泛的同时校准法,使用难度方向性和RMSD等指标进行评价。
1 研究对象
本研究的研究对象是2008年、2009年的两份汉语类别的试卷,其中一份作为基准卷(设为Y卷),另一份作为等值卷(设为X卷),两卷之间包含20%的共同题。
2 研究工具
本研究利用BILOG软件进行等值。研究中涉及的其他程序均使用Visual Foxpro 8.0程序编写。
3 研究方法
等值方法采用同时校准法。
跨样本一致性选择难易方向性和跨样本一致性指标进行检验。
具体做法是:把总体划分为有限的排他的几个样本,然后用总体和样本分别进行等值,进而比较样本等值结果与总体等值结果的差异。差异最小的方法即在不同样本中表现最为一致的方法就是较好的方法。计算选择RMSD和REMSD指标。该方法由Dorans&Holland(2000)首先提出并应用在等组设计中,之后,Von Davier,Holland&Thayer(2003)将RMSD方法延伸到非等组锚题设计中(即共同题设计,NEAT)。
NEAT设计涉及两个被试群体。T是由被试组P和被试组Q按照一定比例组成的综合组。将被试群体P和Q各划分为不同的样本:{Pj}和{Qj}。WPj是指样本Pj的相应权重,WQj表示Qj在Q中的相应权重。WPj和WQj可被设定为某个值,只要总和为1。由此可知:
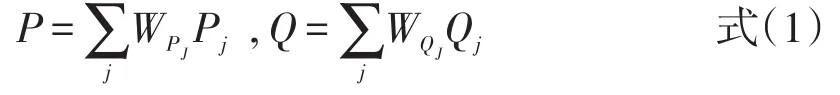
对于P和Q的样本{Pj}和{Qj},也有相应的样本综合组Tj,可以定义为:

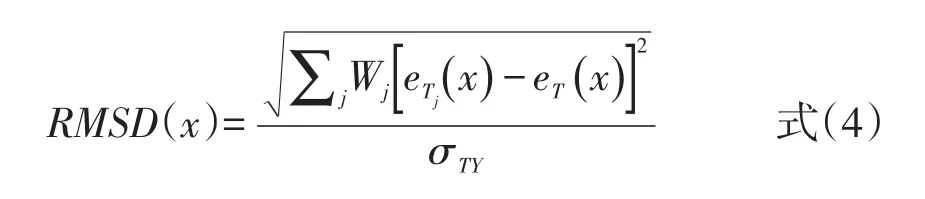
由于Y卷分数在综合组T中并不能直接观测到,因此综合组T中Y卷分数的标准差σYT的计算依赖于所选的等值方法。由公式可知,X卷上的每一个分数点对应到Y卷上都能计算出一个RMSD值,有的RMSD值比较小,有的则比较大,这样我们就无法直接客观地得出跨样本是否一致的结论。为了得到单一值,可计算REMSD指标,即期望的差异平方根。
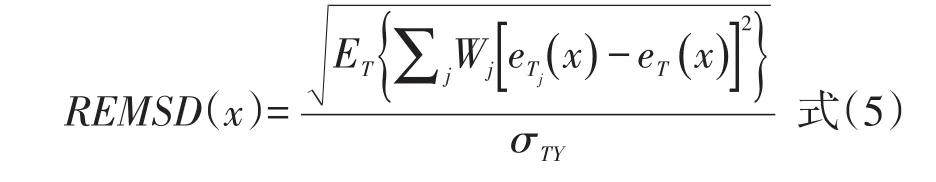
式(5)中,ET{}是指T组在X卷上分布的平均数。
在计算统计量时,需要考虑的问题是统计量达到多大就可认为是显著的,即RMSD值和REMSD值都需要一个标准来衡量。Dorans,Holland,Thayer &Tateneni(2003)建议用DTM(Difference That Mat-ters)这个指标。ETS多年来也是采用了这个标准。DTM是指报告分数的半个单位,即采用四舍五入时可以忽略分数的一半。例如在该测验分数中,以1为分数单位,此时DTM=0.5。由于RMSD和REMSD这两个统计量通过σYT实现标准化,DTM也常常用它来实现标准化,标准化后的DTM常常用SDTM表示。
4 研究结果
4.1 试卷单维性
利用SPSS软件进行因素分析,如果数据满足单维性要求,则说明试卷符合IRT的理论假设,可以进行IRT等值(见表1)。
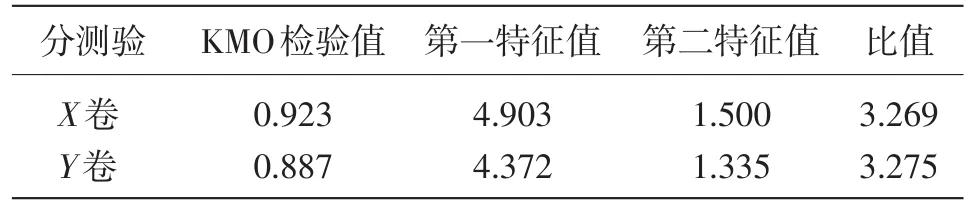
表1 试卷因素分析结果
表1中,两卷KMO检验值均接近1,说明样本采集充足度高,因素分析的结果可以接受;两份试卷的第一特征值均超过第二特征值的3倍。根据Hambleton&Swaminathan(1985)的单维性检验标准,第一特征值大于第二特征值的3倍,就可以认为测验是单维的。由此判断,测验考查的潜在特质是单一的,考生的作答主要受到了所要考查的特质的影响,符合了IRT理论的基本假设。
4.2 分析试卷质量
对共同题得分和测验总分进行相关分析,得到相关系数为0.77,相关较高;由于共同题均由专家挑选,并按照内容模块、难度等指标选择具有良好代表性的题目,因此共同题是的试卷的代表性样本。
X卷、Y卷被试人数均超过2 000人,样本量充足,满足IRT理论的样本量要求。由表2可见,三个模型下的参数估计结果并不相同,这和函数解析式不同有关,因为不同的模型中参数数量不同,对项目特征曲线的描述也会不同。
具体来看,1PLM下,平均b值都在(-3,3)的区间内,说明难度适中;2PLM下,平均难度中等,平均a值都在0.5以上,说明题目的区分度良好;3PLM下,难度中等、区分度较高、c值都在0.25以下,说明考生答题的猜测概率较低。
总体分析,试卷难度适中,区分度良好,猜测度低,试卷整体质量良好。
4.3 跨样本一致性检验
评价方法包括难易方向的一致性和跨样本RMSD和REMSD值。若RMSD和REMSD值都小于SDTM值,并且值越小,则说明跨样本一致性越高。
4.3.1 样本拆分
跨样本分析的前提是拆分的子样本应是总体的代表性样本,所以要对样本进行代表性检验。步骤如下:
参加X卷的考生群体为P,共有7 298人;参加Y卷的考生群体为Q,共有2 258人。把考生群体P和考生群体Q随机分为两个独立的人数相等的样本,并通过独立样本T检验来检验四个样本的代表性(见表3)。
(1)样本P1、P2对总体P的代表性检验
由表4、表5可知,双尾检验下、方差齐时显著性水平P1为0.915,P2为0.915,均远远大于临界值的显著性水平0.01。因此,样本P1、样本P2和总体P在α=0.01水平下,没有显著差异。同样,我们进行了样本Q1和样本Q2代表性检验,差异不显著,因此样本P1和样本P2都是总体P的代表性样本,样本Q1和样本Q2也是总体Q的代表性样本。

表2 试卷平均参数信息

表3 随机拆分样本数量表
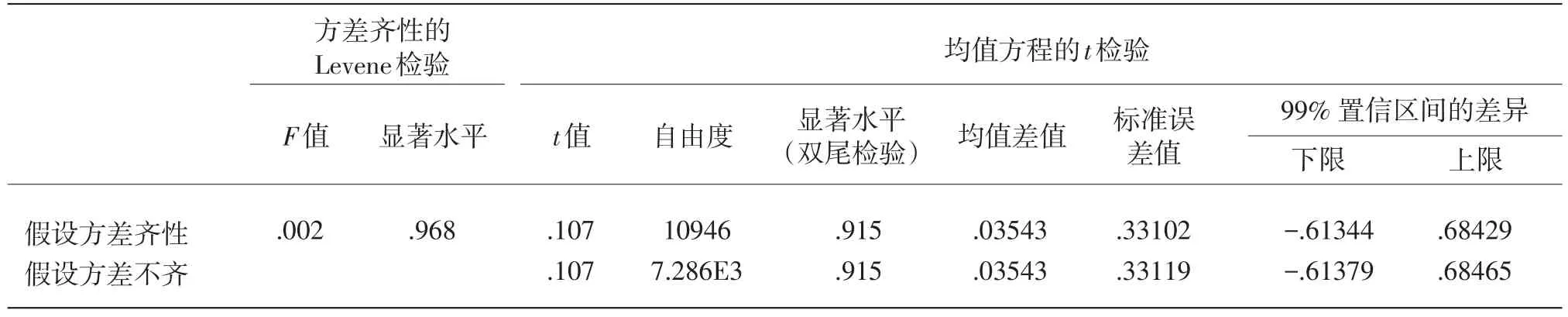
表4 P1的样本代表性检验
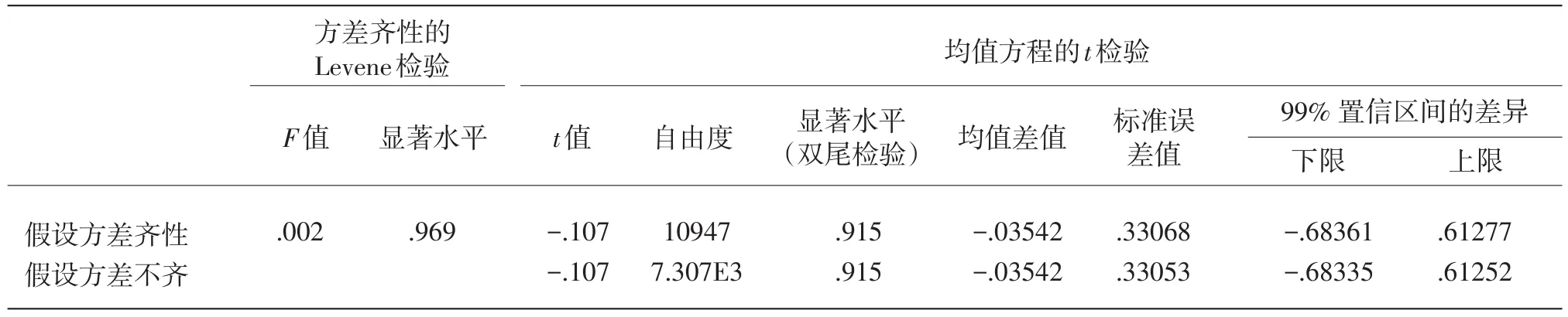
表5 P2的样本代表性检验
4.3.2 难易方向性分析
针对总体数据和四个代表性样本,分别用三种模型下的同时校准法等值。比较基于总体和基于样本的等值结果,以此来分析试卷难易的方向性。如果难易方向性一致,那么我们可以粗略地认为等值的跨样本是一致的,等值框架如图1所示。
等值的难易方向性是指排除考生能力水平差异的影响,待等值卷(X)相比基准卷(Y)是偏难还是偏易,这主要根据平均数附近的等值结果来比较。限于篇幅,本研究只列出2PLM下的同时校准法(下称同时校准双参数法)平均数附近的数据加以说明。
从表6可知,用同时校准双参数方法把X卷等值到Y卷上,基于总体P、Q得到的等值结果与基于样本P1、P2、Q1、Q2得到的等值结果在试卷的难易方向性上一致,即基于总体P、Q得到的等值结果表明X卷比Y卷难,因此等值后的分数高于原始分数;同样地基于样本得到的等值结果也认为X卷比Y卷难。同时校准单参数方法的难易方向性也大体一致,但跨样本的数值出现了一些波动,而同时校准三参数法由于等值中出现了参数漂移,因此难易方向性并不一致,说明跨样本不稳定,因此下文的跨样本一致性比较仅在同时校准单参数法和同时校准双参数法之间比较。
4.3.3 跨样本一致性指标计算

图1 等值框架
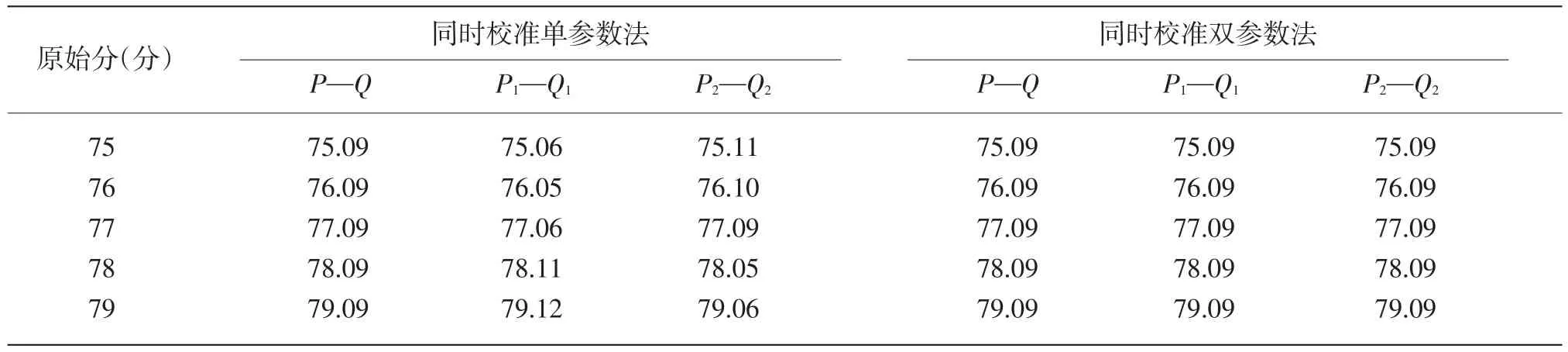
表6 同时校准双参数法等值后基于总体和基于样本的等值分数表
在难易方向基本一致的基础上,计算同时校准单参数法和同时校准双参数法的RMSD和REMSD值,从而更精确地检验等值的跨样本情况。结果如图2、图3、表7所示。
(1)RMSD值——同时校准单参数法
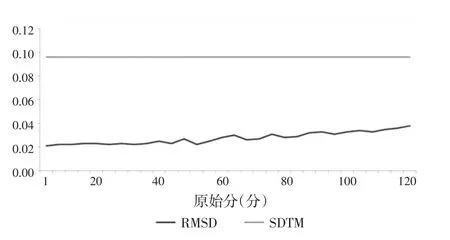
图2 同时校准单参数等值的RMSD值
(2)RMSD值——同时校准双参数法
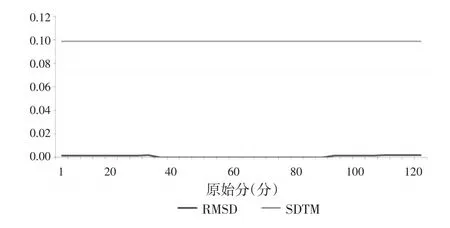
图3 同时校准双参数等值的RMSD值
(3)REMSD值
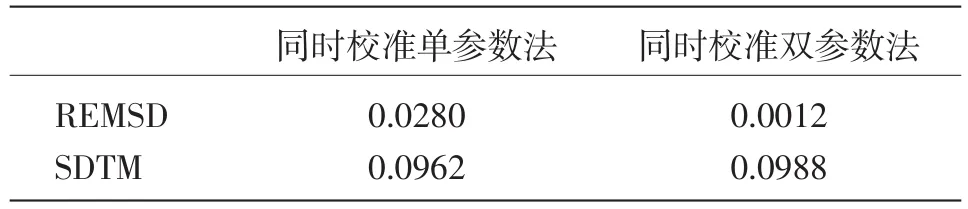
表7 测验REMSD值及相应SDTM指标
5 研究结论
图2、图3的RMSD值表明,每个分数点的RMSD值都低于SDTM指标。说明两种方法中基于样本得到的等值结果与基于总体得到的等值结果十分相近。同样地,表7中的REMSD值显示,每个测验的REMSD值都远远低于SDTM指标。说明测验等值都实现了跨样本一致,基于样本得到的等值结果与基于总体得到的等值结果一致。
具体来看:在同时校准双参数方法的难易方向性比单参数法更一致,而且从等值后的转换分数来看,基于总体和基于样本的等值分非常接近,几乎没有太多变化,而单参数出现一些波动。从RMSD、REMSD指标来看,两种方法实现了跨样本一致,对比数据发现双参数法的RMSD、REMSD值更小,而且各分测验中每个原始分对应的RMSD都保持稳定,没有起伏,而单参数法中原始分对应的RMSD值在分数两端或者中间部分都出现了一定程度的起伏。综上所述,同时校准双参数法的的跨样本更稳定。
6 研究中的不足
本研究主要选择了IRT等值方法中最常用的同时校准法进行跨样本一致性的比较,鉴于时间和精力有限,所以未对其他等值方法进行探索,因此对其他方法在不同模型中的跨样本表现进行分析将成为进一步研究的方向。
[1]Dorans,N.J.,&Holland,P.W.Population invariance and the equat-ability of tests:Basic theory and the linear case[J].Journal of Educa-tional Measurement,2000,37(4):281-306.
[2]Dorans,N.J.,Holland,P.W.,Thayer,D.T.,&Tateneni,K.Invariance of scoring across gender groups for three Advanced Placement Pro-gram examinations[C].In N.J.Dorans,(Ed.),Population invariance of score linking:Theory and applications to advanced placement pro-gram examinations.(ETS RR-03-27,pp.79-118).Princeton,NJ: Educational Testing Service,2003.
[3]Hambleton,R.K.,&Swaminathan,H.Item response theory:Princi-ples and applications[M].Boston,MA:Kluwer-Nijhoff,1985.
[4]Holland,P.W.,&Rubin,D.B.ed.Test equating[M].New York:Ac-ademic Press,1982.
[5]Von Davier,A.A.,Holland,P.W.,&Thayer,D.T.Population invari-ance and chain versus post-stratification methods for equating and test linking[C].In N.Dorans(Ed.),Population invariance of score linking:Theory and applications to advanced placement program ex-aminations(ETS RR-03-27,pp.19–36).Princeton,NJ:ETS,2003.
Study on Cross-sample Consistency under Concurrent Calibration Equating Method of Three IRT Models
ZHANG Quanhui&HUANG Huiying
This study attempts to analyse the Cross-sample Consistency in three types of Logistic model.The object of study is some kind of Chinese character test,with the Concurrent calibration equating method.The result is that the method of Concurrent calibration is more stable in Cross-sample Consistency.
IRT;LOGISTIC Model;Concurrent Calibration;Cross-sample Consistency
G405
A
1005-8427(2016)02-0003-6
更正启示
《中国考试》杂志社
张泉慧,女,国家医学考试中心,副主任科员(北京 100097)
黄慧英,女,教育部民族教育发展中心,博士研究生(北京 100082)
《中国考试》第12期李峰、王蕾、焦丽亚所著“预测高考考生能力水平调控高考试题难度研究探新”一文,其课题名称为“教育部考试中心‘高考考生能力水平预测’课题研究相关成果。”特此更正。
