非线性奇摄动反应扩散问题的广义渐近解*

史娟荣，陈贤峰，莫嘉琪

(1. 安徽机电技术学院，安徽 芜湖 241002；2. 上海交通大学数学系，上海 200240；3. 安徽师范大学数学系，安徽 芜湖 241003)

非线性奇摄动反应扩散问题的广义渐近解*

史娟荣1,2，陈贤峰2，莫嘉琪3

(1. 安徽机电技术学院，安徽 芜湖 241002；2. 上海交通大学数学系，上海 200240；3. 安徽师范大学数学系，安徽 芜湖 241003)

研究了具有内部激波的非线性反应扩散方程奇摄动广义初始边值问题。在适当的条件下， 讨论了退化问题的广义外部解并引入伸长变量，构造了原问题具有内部激波和初始层校正项的广义解的形式渐近展开式。最后，利用泛函分析不动点理论得到了原初始边值问题广义解的存在性和一致有效的内部激波广义渐近解。

非线性；激波；渐近解

非线性奇异摄动激波问题是目前在数学界十分重视的一个课题[1-2]。近来许多学者的研究中涉及到这一方面的工作[3-7]。作者等也讨论了一类奇摄动非线性激波、孤立子、冲击层等问题[8-22]。本文用特殊的方法来考虑一类广义反应扩散奇摄动激波问题。

考虑如下问题：

εut-uxx=f(t,x,u),

(t,x)∈(0,T0)×(-1,1)

(1)

u=g(t,x),x∈±1

(2)

u=h(x),t=0

(3)

其中ε为正的小参数，T0为一个足够大的正常数。

假设：

[H1]f除了在x0∈(-1,1)以外和g,h关于其自变量在对应的区域内为充分光滑的函数，g(0,x)=h(x),x∈(-1,1)；

[H2] 存在常数δ>0，使得

代替问题(1)-(3)，我们考虑如下广义反应扩散初始边值问题：

(4)

(5)

(6)

其中

我们还假设:

[H3]退化问题

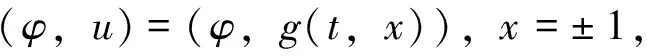
有一个广义解U0(t,x)，但在x0∈(-1,1)处

1 外部解

设问题(4)-(6)的广义外部解U为

(7)

将(7)式代入(4)式, (5)式, 按ε展开非线性项，合并ε的同次幂项，并令其系数为零。对于εi,i=0,1,…，可得

B1[φ,U0]=-(φ,f(t,x,U0)),

(t,x)∈(0,T0)×(0,1)),

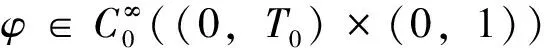
(8)

(φ,U0)=(φ,g(t,x)),x=±1,

(9)

B1[φ,Ui]=-(φ,fu(t,x,U0)Ui+Fi)-(φ,DUi-1),

(t,x)∈(0,T0)×(-1,1),

i=1,2,…

(10)

(φ,Ui)=0,x=±1,

(11)

其中Fi(i=1,2,…)为依次已知的函数，其结构从略。

由假设[H3]，广义初值问题(8)-(9)存在广义解U0(t,x)，再由线性问题(10)-(11)，可依次得到广义解Ui(t,x),i=1,2,…。将它们代入(7)式便得到问题(4)-(6)的广义外部解U。但外部解U在(t,x0)∈(0,T0)×(-1,1)处间断，而且未必满足条件(6)。为此我们尚需在(t,x0)∈(0,T0)×(-1,1)附近构造广义内部激波层校正项V和在t=0附近构造广义初始层校正项W。

2 广义内部激波层校正项

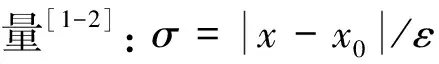
(12)

(13)

其中

设

u=U+V

(14)

这里

(15)

将(14)-(15)式代入(12)-(13)式，按ε展开非线性项，合并ε的同次幂项，并令其系数为零。对于εi,i=0,1,…，可得

(16)

(17)

(18)

(19)

(20)

(21)

由(16)-(18)式和(19)-(21)式，依次地得到vi(t,σ)(i=0,1,…)，并且由假设知vi(t,σ)具有内部激波层性态：

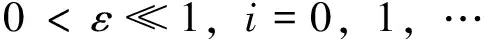
(22)

这里ki(i=0,1,…)为正常数。

将vi(i=0,1,…)代入(15)式，便得到奇摄动反应扩散问题(4)-(6)广义解u的内部激波层校正项V。

3 广义初始层校正项

作伸长变量的变换

(23)

并设

u=U+W

(24)

其中

(25)

考虑到(23)式，将(24)-(25)式代入(4)-(6)式，并把各项按ε的幂进行展开。取εi,i=0,1,2的系数的代数和为零。可得

f(0,x,U0+w0)-(φ,f(0,x,U0),

(26)

(27)

(28)

(29)

(30)

(31)

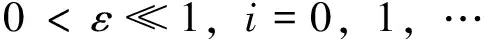
(32)

再令

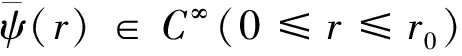
因此，wi为具有初始层校正项性态的函数。将所得的结果代入(25)式，我们便得到奇摄动反应扩散初始边值问题(4)-(6)解u的广义初始层校正项W。

于是我们便构造了反应扩散奇摄动问题(4)-(6)广义解u的如下形式渐近展开式：

(33)

4 广义解的一致有效性

设

由(22) 式，(32)式，对于充分小的ε，使得

故由假设和泛函分析不动点理论[1-2]，可得

于是有如下定理：

定理1 在假设[H1]-[H3]下，对于充分小的ε，奇摄动反应扩散广义初始边值问题(4)-(6)在H1((0,T0)×(-1,1)意义下存在一个广义解u，且解u具有形如(33)式的一致有效的渐近展开式，成立

[1]DEJAGEREM,JIANGFR.Thetheoryofsingularperturbation[M].Amsterdam:North-HollandPublishingCo, 1996.

[2]BARBUL,MOROSANUG.Singularlyperturbedboundary-valueproblems[M].Basel:BirkhausermVerlagAG, 2007.

[3]MARTINEZS,WOLANSKIN.Asingularperturbationproblemforaquasi-linearoperatorsatisfyingthenaturalconditionofLieberman[J].SIAMJMathAnal, 2009, 41(1): 318-359.

[4]KELLOGGRB,KOPTEVANA.Singularlyperturbedsemilinearreaction-diffusionprobleminapolygonaldomain[J].JDifferEquations, 2010, 248(1): 184-208.

[5]TIANCR,ZHUP.Existenceandasymptoticbehaviorofsolutionsforquasilinearparabolicsystems[J].ActaApplMath, 2012, 121(1): 157-173.

[6]SKRYNNIKOVY.Solvinginitialvalueproblembymatchingasymptoticexpansions[J].SIAMJApplMath, 2012, 72(1): 405-416.

[7]SAMUSENKOPF.Asymptoticintegrationofdegeneratesingularlyperturbedsystemsofparabolicpartialdifferentialequations[J].JMathSci, 2013, 189(5): 834-847.

[8]MOJQ,CHENXF.HomotopicmappingmethodofsolitarywavesolutionsforgeneralizedcomplexBurgersequation[J].ChinPhysB, 2010, 10(10): 100203.

[9]MOJQ,HANXL,CHENSL.Thesingularlyperturbednonlocalreactiondiffusionsystem[J].ActaMathSci, 2002, 22B(4): 549-556.

[10]MOJQ,LINWT,WANGH.Variationaliterationsolutionofasea-airoscillatormodelfortheENSO[J].ProgNatSci, 2007, 17(2): 230-232.

[11]MOJQ,LINWT.Aclassofnonlinearsingularlyperturbedproblemsforreactiondiffusionequationswithboundaryperturbation[J].ActaMathApplSinica, 2006, 22(1): 27-32.

[12]MOJQ.Aclassofsingularlyperturbeddifferential-differencereactiondiffusionequation[J].AdvMath, 2009, 38(2): 227-231.

[13]MOJQ.Homotopivmappingsolvingmethodforgainfluencyofalaserpulseamplifier[J].ScienceinChina(SerG), 2009, 52(7): 1007-1070.

[14]MOJQ,LINWT.Asymptoticsolutionofactivatorinhibitorsystemsfornonlinearreactiondiffusionequations[J].JSysSci&Complexity, 2008, 20(1): 119-128.

[15]MOJQ.ApproximatesolutionofhomotopicmappingtosolitarywaveforgeneralizednomlinearKdVsystem[J].ChinPhysLett, 2009, 26(1): 010204.

[16]MOJQ.Singularlyperturbedreactiondiffusionproblemfornonlinearboundaryconditionwithtwoparameters[J].ChinPhys, 2010, 19(1): 010203.

[17] 史娟荣, 石兰芳, 莫嘉琪. 一类非线性强阻尼扰动发展方程的解[J]. 应用数学和力学, 2014, 35(9):1046-1054.

[18]SHIJR,LINWT,MOJQ.Thesingularlyperturbedsolutionforaclassofquasilinearnonlinearproblemforhigherorderwithtwoparameters[J]. 南开大学学报(自然科学版), 2015, 48(1): 85-91.

[19]WANGWG,SHIJR,SHILF,etal.Thesingularlyperturbedsolutionofnonlinearnonlocalequationforhigherorder[J]. 南开大学学报(自然科学版), 2014, 47(1): 13-18.

[20]MOJQ,CHENXF.HomotopicmappingmethodofsolitarywavesolutionsforgeneralizedcomplexBurgersequation[J].ChinPhysB, 2010, 19(10): 100203.

[21] 莫嘉琪，陈贤峰. 一类非线性扰动Nizhnik-Novikov-Veselov系统的孤立波近似解析解[J].物理学报, 2010, 50(5): 2919-2923.

[22] 莫嘉琪，陈贤峰. 一类广义非线性扰动色散方程孤立波的近似解[J]. 物理学报, 2010, 50(3): 1403-1406.

The generalized asymptotic solution for nonlinear singular perturbation reaction diffusion problem

SHIJuanrong1,2,CHENXianfeng2,MOJiaqi3

(1. Anhui Technical College of Mechanical and Electrical Engineering, Wuhu 241002, China;2. Department of Mathematics, Shanghai Jiaotong University, Shanghai 200240, China;3. Department of Mathematics, Anhui Normal University, Wuhu 241003, China)

The nonlinear singular perturbation interior layer initial boundary value problem for the reaction diffusion equation is considered. Under suitable conditions, the reduced problem generalized outer solution is discussed. By introducing a stretched variable, the formal asymptotic expansion for the generalized solution with interior layer and initial layer corrective terms is constructed. Finally, using the fixed point theory of functional analysis, the existence and uniformly valid interior shock asymptotic solution for the original initial boundary value problems are proved.

nonlinear; shock; asymptotic solution

10.13471/j.cnki.acta.snus.2016.02.005

2015-04-08

国家自然科学基金资助项目(11371248)；安徽省高等学校省级自然科学研究资助项目(KJ2015A418)

史娟荣(1981年生)，女；研究方向：应用数学;E-mail:ahjdshjr@126.com

O

A

0529-6579(2016)02-0023-05