移动机械臂的协调运动方案设计及验证*

肖 林，周文辉

(吉首大学信息科学与工程学院，湖南 吉首 416000)

移动机械臂的协调运动方案设计及验证*

肖 林，周文辉

(吉首大学信息科学与工程学院，湖南 吉首 416000)

移动机械臂是由一个移动平台和一个固定在其上面的机械臂组成。为了能实现对移动机械臂的协调控制，移动平台和机械臂不得不同时完成任务。通过对移动机械臂的运动学建模分析，提出了一个基于最小速度范数的协调运动方案。该方案不仅可以实现对移动平台的运动控制，而且可以对机械臂同时进行协调控制。此外，协调运动方案可以等效的转换为一个标准二次规划问题，进而可以开发出一个有效的数值算法去求解。最后，移动机械臂去执行一个圆形路径，对应的仿真结果验证了协调运动方案的有效性。

移动机械臂；二次规划；协调运动；数值算法

20世纪以来, 随着自动化技术的成熟和发展, 机器人作为一种复杂和先进的机电系统出现在生产与科研等多个方面[1-2]。控制机器人的一个基础问题是实时的冗余度解析问题(或称实时运动规划)；即，给出机器人末端执行器的运动轨迹，如何实时地得到各关节的变化情况[1-6]。在过去30年里，科研工作者提出了各种计算方案来实现机器人的冗余度解析。而且，通过适当地求解冗余度解析问题，机器人在执行给定的末端执行器任务时，就可以躲避环境障碍物、关节的物理极限和关节奇异等[3-4]。

移动机械臂，作为智能机器人的一种，在军事、工业和服务等领域已经得到了实际应用[3,5]。和固定机械臂相比，移动机械臂拥有更大的移动范围以及更强的作业能力，因此得到了广泛的关注。然而，移动平台和冗余机械臂之间的组合也带来了一些新的困难：怎么样同时协调控制移动平台和机械臂的运动？就一般规划方案而言，要么是先控制移动平台的运动，后控制机械臂的运动；要么是先控制机械臂的运动，后控制移动平台的运动，从而无法对移动平台和机械臂同时进行协调控制[3]。Cheng等[7]在动力学环境不确定情况下，实现了对轮式移动机械臂的智能控制算法。Tang等[8]对轮式移动机械臂的规划和控制提出了基于微分平滑理论和实验。Xu等[9]对全方位的轮式移动机械臂的轨迹追踪控制提出了基于鲁棒神经网络的滑动模态方法。Andaluz等[10]针对轮式移动机械臂的视觉反馈控制提出了动力学补充方法，并分析了相关增益性能。Wang等[11]针对不确定约束下的非完整移动机械臂的控制提出了一套自适应递归神经网络方法。Xiao和Zhang[12-13]分别针对六连杆机械臂和轮式移动机械臂提出了加速度重复运动方案和逆运动学求解方案，并对相应的神经网络求解器进行了理论分析。

本文设计的移动机械臂协调运动方案就是对移动平台和机械臂同时进行协调控制运动，从而使得移动机械臂更加有效地完成给定的末端任务。

1 运动学建模分析

让我们考虑一个轮式移动机械臂，它由一个轮式移动平台和一个空间六自由度机械臂组成[2-3]。为了完备性，图1给出了轮式移动平台的运动学分析模型。在本节中，将先分析了移动平台的运动学建模，然后直接给出空间机械臂的运动学方程，最后，将机械臂与移动平台的运动学方程进行联合统一，最终得到该轮式移动机械臂的运动学模型。

1.1 移动平台的运动学建模

在本文中，我们是在非完整性约束性条件下建立移动平台的数学模型[4-6]。为了更好的理解，如图1所示，我们在建模的过程中使用了以下这些符号。

Po：两个驱动轮轴的中点，它的三维坐标是(xo,yo,zo)；

Pc：机械臂和移动平台的连接点，它的三维坐标是(xc,yc,zc)；其中zc=0；

d：点P0和点Pc之间的距离；

a：驱动轮到点P0的距离；

r：驱动轮的半径；

Q：一个假设点，移动平台围绕它转动；

图1 移动平台运动模型Fig.1 Kinematic model of the mobile platform

值得指出的是，移动平台和机械臂的每个连杆都可以看做刚体，且移动平台只在XOY平面运动。所以，在移动平台没有侧滑的条件下，左右轮的的速度方向将严格和驱动轮轴方向垂直。然后根据图1中的几何关系，可以得到：

(1)

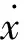
(2)

通过联合方程(1)和(2)，我们可以得到如下表达式：

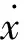
(3)

(4)

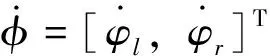
1.2 六自由度机械臂的运动学建模

对于一个固定机械臂，可以直接建立一个关于XCYCZC坐标系的前向运动学模型，即关节空间向量φ∈Rn和末端执行器位置向量rb∈Rm的一个转换关系：

其中f(φ)是一个可微的非线性函数。而且，对于一个给定的机械臂，它的结构和参数是已知的。在本文研究的空间六自由度机械臂的D-H参数[3-6]如表1所示，由此可以得到空间六自由度机械臂的具体运动学方程如下：

l43s32c1+l2s2c1

l65(c5s32s1-s5c4c32s1-s5s4s1)+

l43s32s1+l2s2s1

(5)

其中li表示第i个连杆的长度，ci=cosφi，si=sinφi，i=1,2,3,…6，s32=sin(φ3+φ2)，c32=cos(φ3+φ2)，l0表示第一个关节离移动平台底部的高度，l65=l6+l5，和l43=l4+l3。在该机械臂中，参数l0=0.698 m，l1=0.065 m，l2=0.555 m，l3=0.190 m，l4=0.130 m，l5=0.082 m，l6=0.133 m。

表1 空间六自由度机械臂的D-H参数表

1.3 移动机械臂的集成运动学建模

在这一节中，我们将在移动平台和空间六自由度机械臂与的运动学建模的基础上，建立移动机械臂的集成运动学模型。首先，对于移动机械臂而言，末端执行器的运动是相对于世界坐标系的，而不是基坐标系(即XCYCZC坐标系)，因此通过采用一个从基坐标系到世界坐标系的转换矩阵，将得到基于世界坐标系的移动机械臂集成运动学关系[14-15]：

(6)

其中从基坐标系到世界坐标系的转换矩阵为

注意上式方程是移动机械臂基于世界坐标系在位置层的运动学模型，而通过对方程(6)求其时间导数，我们将得到移动机械臂在速度层的集成运动学模型

(7)

(8)

(9)

其中I表示单位矩阵，增广矩阵K定义如下：

通过以上转换，我们最终得到轮式移动机械臂在速度层上的统一运动学模型(9)。

2 协调运动方案设计

对于移动机械臂，我们不仅要考虑机械臂的物理极限约束，也要考虑移动平台带来的影响。为了能实现在有物理约束的移动机械臂进行协调运动，我们将把机械臂的关节速度变量和移动平台左右轮的旋转速度变量作为一个整体变量，从而设计得到一个基于最小速度范数的二次性能指标。最后，通过联合性能指标、物理约束以及移动机械臂的集成运动学方程，提出一个能实现移动机械臂协调运动的方案。

2.1 协调运动方案

基于以上考虑，利用二次规划的描述，我们设计了如下的协调运动方案：

(10)

(11)

q-≤q≤q+

(12)

(13)

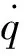
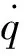
(14)

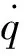
(15)

其中ϑ-和ϑ+的第i个元素分别定义为(i=1,2,3,,…，n+2):

最小化xTWx/2

(16)

(17)

ϑ-≤x≤ϑ+

(18)

2.2 数值算法

当我们把实现移动机械臂的协调运动运动方案(10)-(13)重新表述为标准的二次规划(16)-(18)后，我们将开发和使用一个数值算法来求解我们的协调运动方案(10)-(13)。

首先，从文献[2-3]得知，标准的二次规划(10)-(13)可以等效于如下的成线性投影方程：

(19)

其中PΩ(·):RN→Ω定义为从空间RN到集合Ω的一个分段线性投影算子，其它的参数定义如下：

接下来，为了求解线性投影方程(19)以及二次规划问题(10)-(13)，我们定义一个向量取值的误差函数：

(20)

显然，求解投影方程(19)就等效于找到方程(20)的一个零点。

3 仿真验证

在这一小节中，移动机械臂的末端执行器去跟踪一个半径为0.3m的圆形路径，以此来验证协调运动方案(16)-(18)的有效性。在仿真过程中，迭代公式(21)的最大误差容限设置为1.0×10-5，任务执行时间T=5s。对应的仿真结果分别如下图2-5所示。

图2展示了在整个跟踪过程中移动机械臂的运动轨迹。图3从俯视的角度更加直观的显示了移动机械臂的运动过程。从图2到图3可以得知，移动机械臂在完成圆形任务跟踪的过程中，结束状态和初始状态几乎重合，实现了最小能量消耗，而且在整个跟踪过程当中，移动平台和机械臂一直在协调运动。图4进一步展示了期望的圆形路径和对应的跟踪轨迹，从图中可以看出，实际的跟踪轨迹几乎已经和期望的圆形路径重合。

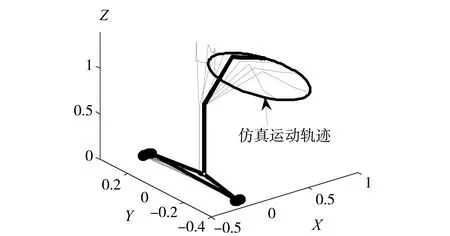
图2 移动机械臂的仿真运动轨迹Fig.2 Simulative motion trajectory of mobile manipulator

图3 移动机械臂的运动轨迹俯视图Fig.3 Top view of motion trajectories of the mobile manipulator

图4 期望的圆形路径和仿真的跟踪轨迹Fig.4 Desired circular path and simulative tracking trajectory

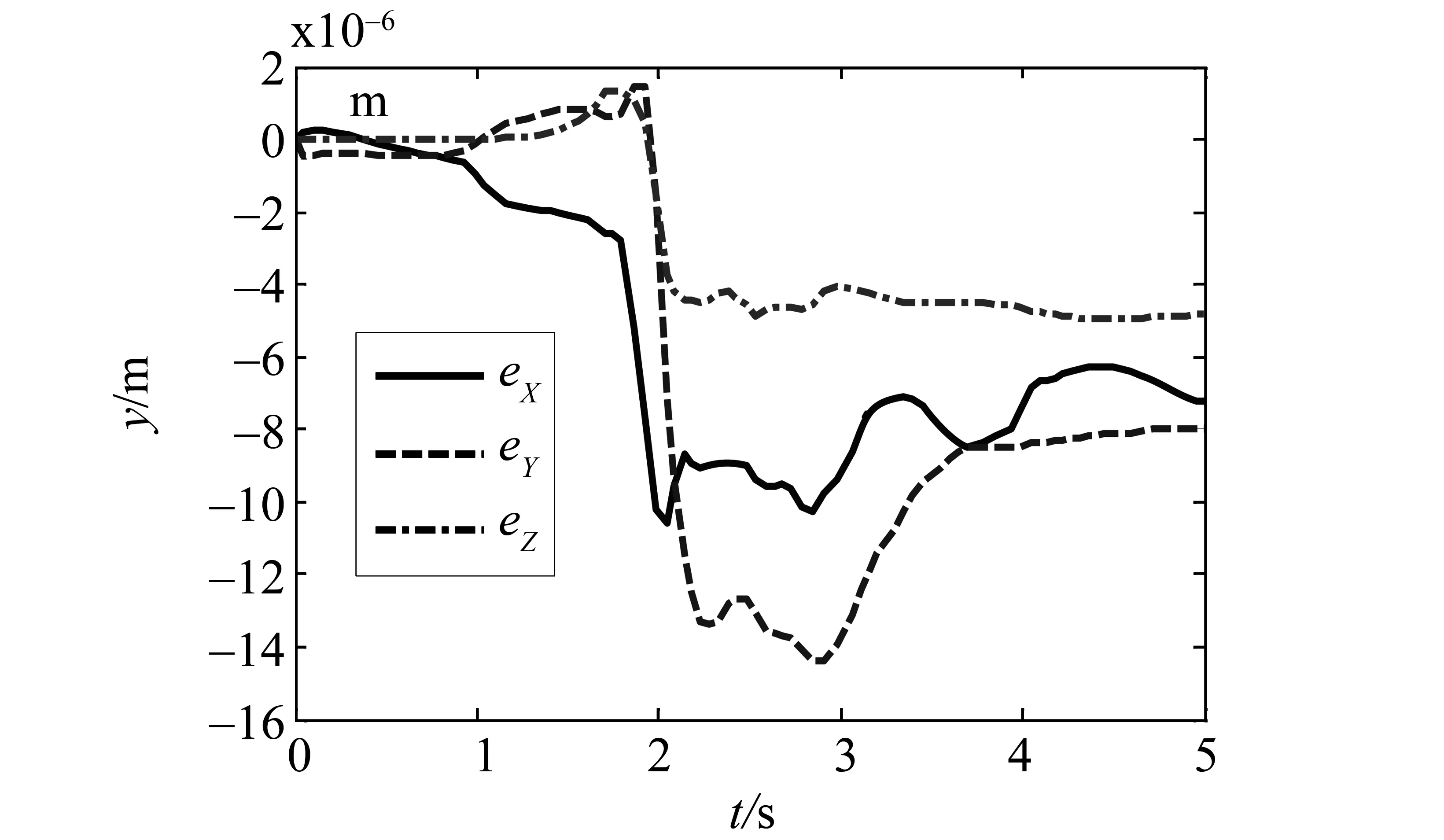
图5 对应的跟踪位置误差Fig.5 Corresponding tracking position error profiles

而且图5显示了它们之间的位置误差e=rw-g(φ,φ)-[xc,yc,0]T，其中eX、eY以及eZ分别代表e的X轴、Y轴以及Z轴分量。如图5所示，跟踪位置误差的X轴、Y轴以及Z轴分量都小于2×10-5m。总之，这些结果都证实了协调运动方案的有效性以及高精度型。

4 结 论

通过分别对移动平台和机械臂的运动学分析，建立了移动机械臂的统一运动学方程。在此基础上，提出了基于最小速度范数的协调运动方案。而且，开发了一个比较有效的数值算法去求解标准的二次规划问题。最后基于轮式移动机械臂的末端执行器期望去跟踪一个圆形路径，验证了协调运动方案的可行性、有效性和高精度性。

[1] 欧阳帆．双机器人协调运动方法的研究[D]. 广州:华南理工大学, 2013.

[2] 张雨浓，谭志国，杨智，等.基于二次型规划的平面冗余机械臂的自运动[J].机器人,2008,30(6):566-571.

[3]XIAOL,ZHANGYN.Anewperformanceindexforrepetitivemotionofmobilemanipulators[J].IEEETransactionsonCybernetics, 2014, 44(2): 280-292.

[4] 郑秀娟．移动机械臂的运动控制与轨迹规划算法研究[D]. 武汉:武汉科技大学, 2012.

[5] 郭秉华.六自由度空间柔性机械臂的动力学分析与控制[D]. 北京:北京邮电大学,2009.

[6] 邓雅.空间机械臂建模及轨迹跟踪控制方法研究[D]. 哈尔滨:哈尔滨工业大学, 2013.

[7]CHENGM,SUW,TSAIC,etal.Intelligenttrackingcontrolofadual-armwheeledmobilemanipulatorwithdynamicuncertainties[J].InternationalJournalofRobustandNonlinearControl, 2013, 23(8): 839-857.

[8]TANGCP,MILLERPT,KROVIVN,etal.Differentialflatnessbasedplanningandcontrolofawheeledmobilemanipulator:Theoryandexperiment[J].IEEE/ASMETransactionsonMechatronics, 2011, 16(4): 768-773.

[9]XUD,ZHAOD,YIJ,etal.Trajectorytrackingcontrolofomnidirectionalwheeledmobilemanipulators:robustneuralnetwork-basedslidingmodeapproach[J].IEEETransactionsonSystems,Man,andCybernetics(PartB):Cybernetics, 2009, 39(3): 788-799.

[10]ANDALUZVH,ROBERTIF,SALINASL,etal.Passivity-basedvisualfeedbackcontrolwithdynamiccompensationofmobilemanipulators:StabilityandL2-gainperformanceanalysis[J].RoboticsandAutonomousSystems, 2015, 66: 64-74.

[11]WANGZ,ZHOUT,MAOY,etal.Adaptiverecurrentneuralnetworkcontrolofuncertainconstrainednonholonomicmobilemanipulators[J].InternationalJournalofSystemsScience, 2014, 45(2): 133-144.

[12]XIAOL,ZHANGY.Solvingtime-varyinginversekinematicsproblemofwheeledmobilemanipulatorsusingZhangneuralnetworkwithexponentialconvergence[J].NonlinearDynamics, 2014, 76(2): 1543-1559.

[13]XIAOL,ZHANGY.Acceleration-levelrepetitivemotionplanninganditsexperimentalverificationonasix-linkplanarrobotmanipulator[J].IEEETransactionsonControlSystemsTechnology, 2013, 21(3): 906-914.

[14] 翁轩，杨龙刚，刘屿，等. 具有边界扰动柔性机械臂的鲁棒自适应边界控制[J]. 中山大学学报(自然科学版), 2015, 54(3): 44-50.

[15] 黄震，罗中良，黄时慰. 一种带时间窗车辆路径问题的混合蚁群算法[J]. 中山大学学报(自然科学版), 2015, 54(1): 41-46.

[16] 张雨浓，王茹，劳稳超，等. 符号函数激励的WASD神经网络与XOR应用[J]. 中山大学学报(自然科学版), 2014, 53(1): 1-7.

Design and verification of coordinated motion scheme for mobile manipulators

XIAOLin，ZHOUWenhui

(School of Information Science and Engineering, Jishou University, Jishou 416000, China)

A mobile manipulator is composed of a mobile platform and a stationary manipulator fixed to the platform. In order to achieve the coordinated motion control of mobile manipulators, the mobile platform and the manipulator have to fulfill tasks simultaneously. According to the analysis of kinematics for the mobile manipulator, a coordinated motion scheme based on the minimum velocity norm is proposed and investigated. Such a scheme can not only control the motion of the mobile platform, but also coordinate the manipulator to complete tasks simultaneously. Besides, the coordinated motion scheme can be converted equivalently to a standard quadratic program, which can be solved by an effective numerical algorithm. Finally, the mobile manipulator is applied to perform a circular path and the corresponding simulative results validate the effectiveness of the coordinated motion scheme.

mobile manipulator；quadratic programming；coordinated motion；numerical algorithm

10.13471/j.cnki.acta.snus.2016.02.010

2015-03-01

国家自然科学基金资助项目(61503152, 61563017, 61561022, 61363073, 61363033)；湖南省教育厅优秀青年资助项目(15B192)；吉首大学2015年实验室开放基金资助项目(JDLF2015013)；吉首大学2015年校级课题资助项目(15JDX020)；吉首大学2015年大学生研究性学习和创新性实验计划资助项目

肖林(1986年生)，男；研究方向：机器人和神经网络;E-mail:xiaolin860728@163.com

TP24

A

0529-6579(2016)02-0052-06