基于神经网络的多孔泡沫金属磁流变液阻尼器模型*

姚行艳， 喻其炳， 陈志强， 李　川

(1.重庆工商大学 检测控制集成系统重庆市工程实验室，重庆 400067；2.重庆工商大学 国家智能制造服务国际科技合作基地，重庆 400067)



基于神经网络的多孔泡沫金属磁流变液阻尼器模型*

姚行艳1,2， 喻其炳1,2， 陈志强1,2， 李川1,2

(1.重庆工商大学 检测控制集成系统重庆市工程实验室，重庆 400067；2.重庆工商大学 国家智能制造服务国际科技合作基地，重庆 400067)

摘要：多孔泡沫金属磁流变液阻尼器是采用泡沫金属储存磁流变液的新型阻尼器。通过磁流变阻尼器的性能试验研究，得到了阻尼力与电流之间的关系，采用BP神经网络，建立了磁流变阻尼器正向模型。结果显示，神经网络模型能准确地预测磁流变阻尼器的阻尼力和控制电流，证明了该方法的有效性，与已有的模型相比，具有精度高，计算简便等特点。

关键词：神经网络；多孔泡沫；磁流变液；阻尼器

多孔泡沫金属磁流变液阻尼器是一种新型的半主动控制器件，将其应用于被控系统，建立合理的滞回模型，对于深入理解阻尼器特性具有极其重要的意义。关于磁流变液阻尼器的建模研究，目前主要分为两类：参数化建模和非参数化建模。Bingham模型和Bouc-Wen模型是典型的两类参数化模型，而后基于这两种模型又提出了许多力学模型。但Bingham并不能很好地描述磁流变液阻尼器的非线性动态特性问题，非线性Bouc-Wen模型由于模型中参数过多(多达14个以上待定参数)，虽然能够很好地模拟磁流变液阻尼器的滞后特性，却很难将其应用于实际控制器[1-4]。

基于参数化模型的不足，众多学者提出了非参数化模型，其中以多项式模型和神经网络模型最具代表性。S.B.Choi等根据加速度方向的不同，将磁流变液阻尼器的滞回环分为正负两部分，尽管能很好地拟合高于五阶的阻尼力滞回特性，但精度不高[5]。通过模仿动物神经网络特征的神经网络模型，能够根据系统复杂度调节网络内各节点之间的连接关系，具有分布式处理信息的能力。神经网络以其自学习、自组织、联想和记忆及并行处理的特点，已应用于许多领域[6]。为此，论文结合多孔泡沫金属磁流变液阻尼器的实验数据，采用神经网络的方法对多孔泡沫金属磁流变液阻尼器的模型进行建模。

1BP神经网络基本原理

神经网络以现代神经科学为基础，最常见的主要有BP神经网络和Hopfield神经网络。BP神经网络是一种基于误差反向传播的多层前向网络，由输入层、隐含层和输出层构成网络结构，同层节点之间无关联，不同层节点前向连接。研究表明，BP神经网络已经能够解决大部分实际问题。

由上可知，要建立BP神经网络模型，就是要确定神经网络的拓扑结构及其相应的参数，即输入输出、激活函数、误差计算及学习算法。如图1所示给出了一种典型的BP神经网络拓扑结构。

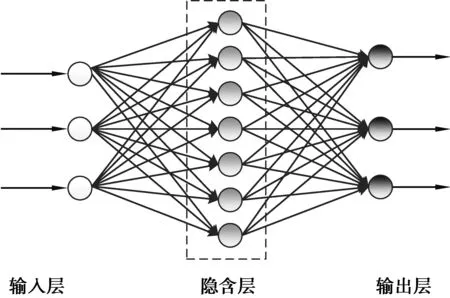
图1　一种典型的BP网络结构拓扑结构Fig.1　Topological structure of BP neural network

1.1节点输出模型

隐含层节点输出：

(1)

输出层节点输出：

(2)

其中，f是激活函数，θ是神经单元阈值。

1.2激活函数

在利用神经网络处理信息的过程中，激活函数起着至关重要的作用,激活函数反映了输出向量与激活状态之间的关系。在BP神经网络中，一般取Sigmoid函数：

(3)

1.3误差函数

误差函数反映了神经网络的期望输出向量与实际输出之间的误差大小：

(4)

1.4学习方式及隐含层节点确定

神经网络的训练过程实际上就是不断修正误差的过程，主要通过调节各层节点之间的权重wij来实现。神经网络的隐含层节点起到承上启下的作用，用来连接输入向量和输出值，同时还进行相应的非线性变换。隐含层节点数目对神经网络的网络性能至关重要。隐含层数目太多，学习时间就会太长，降低网络学习效率，从而使网络不收敛；但隐含层节点数目太少，又会降低网络的容错性。目前，还没有明确的表达式来确定隐含层数目，这里，参考式(5)计算隐含层节点数L[7]：

L=2n+1

(5)

其中，n为输入节点数。

2多孔泡沫金属磁流变液阻尼器BP神经网络建模

多孔泡沫金属磁流变液阻尼器建模，实际上就是将多孔泡沫金属磁流变液阻尼器在算法设计中以BP神经网络模型来代替，通过实验数据训练BP神经网络模型，直至最终逼近阻尼器的阻尼力特性。

2.1BP神经网络拓扑结构的确定

由于多孔泡沫金属磁流变液阻尼器的阻尼特性的影响因素除了电流外，还与活塞的运动速度、位移、温度等有关。针对某类型多孔材料，阻尼力是外加电流i和活塞运动速度v的函数。为此，这里采用电流和速度变量作为输入单元，阻尼力F则为唯一输出单元。一旦确定了输入单元和输出单元数量后，就可以得到中间隐含层单元数目，这里采用5个隐含层单元。如图2所示为其网络拓扑结构。

图2　构建的BP神经网络拓扑结构Fig.2　Topological sturcture of BP neural network

2.2隐含层激活函数的选择

BP神经网络隐含层的激活函数，必须满足处处可微的条件，这里选择S型函数作为中间层传递函数：

(6)

(7)

得到多孔泡沫金属磁流变液阻尼器神经网络结构的输出函数为

(8)

其中，yi为神经网络的输出阻尼力，Fi和fi分别为输出层和隐含层的激活函数，uk和wjk分别为神经网络的输入层向量和权重值，wj0和w0分别为输入层单元和隐含层单元的阈值，wij为隐含层单元的阈值。

2.3神经网络训练过程

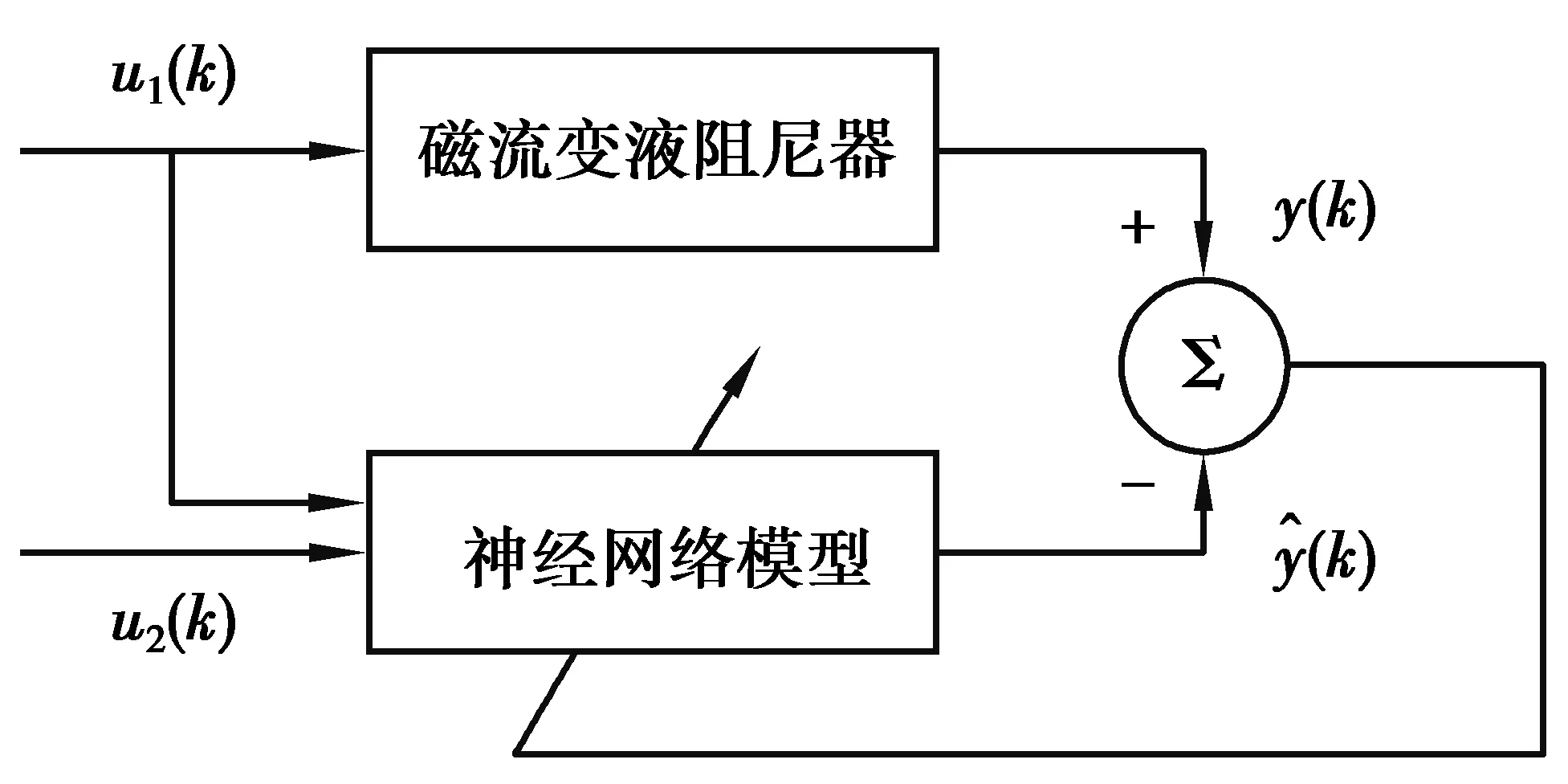
图3　神经网络模型训练Fig.3　Training of neural network

训练数据集：

(9)

其中，N为样本数目。

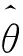
(10)

训练过程中采用均方根误差作为误差函数，其正则表达式如下：

其中，D为正则矩阵。

基于LM算法的训练过程中，其搜索方向为

(12)

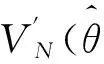
定义VN(θ(i),ZN)的预测方程：

(13)

其中μ(i)为搜索步长，且有：

(14)

r(i)越大，LN(θ(i)+μ(i)f(i))越接近于VN(θ(i)+μ(i)f(i),ZN)。

3训练结果

基于实验阻尼力与外加电流的关系，论文对多孔泡沫金属磁流变液阻尼器的BP神经网络模型进行了训练，最终得到阻尼力与电流的关系如图4所示。从图中可以看到，经过BP神经网络模型训练后的阻尼力和实验阻尼力一致性较好。阻尼力随着外加电流的增加而增大。

图4　神经网络模型训练结果Fig.4　Training results of neural network

4结束语

根据得到的阻尼力特性，结合实验数据，建立了BP神经网络预测模型，结果发现神经网络预测得到的结果与实验结果吻合较好，说明所建立的神经网络预测模型是正确的。为多孔泡沫金属磁流变液阻尼器的应用奠定了良好的技术基础。

参考文献(References)：

[1] YAN Y X,HUI L X,YU M,et al.Dynamic Response Time of a Metal Foam Magneto-rheological Damper[J].Smart Materials and Structures,2013,22(2):1-8

[2] YAO X Y,YU M,FU J.Magnetic-enhanced Normal Force of Magne-torheological Fluids[J].Smart Materials and Structures,2015,24(3):1-9

[3] WANG D H,LIAO W H.Magnetorheological Fluid Dampers:A Review of Parametric Modelling[J].Smart Materials and Structures,2011,20(2):1-34

[4] WANG D H,LIAO W H.Magnetorheological Fluid Dampers:A Review of Parametric Modelling[J].Smart Materials and Structures,2011,20(2):023001

[5] CHOI S B,LEE S K,PARK Y P.A Hysteresis Model for the Field-dependent Damping Force of A Magnetorheological Damper[J].Journal of Sound and Vibration,2001,245(2):375-383

[6] 郭晶,孙伟娟.神经网络理论与MATLAB7实现[M].北京：电子工业出版社,2005

GUO J,SUN W J.Neural Network and MATLAB7 Realize[M].Beijing:Electronic Industry Press,2005

[7] R H N.Applications of Counterpropagation Networks[J].Neural Networks,1988(2):131-139

[8] XIA P Q.An Inverse Model of MR Damper Usingoptimal Neural Network and System Identification[J].Journal of Sound and Vibration,2003(266)：1009-1023

[9] 张红辉.磁偏置内旁通式磁流变阻尼器研究 [D].重庆：重庆大学,2006

ZHANG H H.Study on Inner Bypass Magnetorheological Damper with Magnetic Bias[D].Chongqing:Chongqing University,2014

[10] 姚行艳.基于多孔泡沫金属的磁流变液阻尼器关键机理及性能研究[D].重庆：重庆大学，2014

YAO X Y.Study on the Key Mechanism and Charac-terization of Magnetorheologicall[D].Chongqing:Chongqing University,2014

责任编辑：李翠薇

A Neural Network Model of Porous Metal Foam Magnetorheological Fluid Damper

YAO Xing-yan1,2, YU Qi-bing1,2, CHEN Zhi-qiang1,2, LI Chuan1,2

(1.Chongqing Engineering Laboratory for Detection Control and Integrated System,Chongqing Technology and Business University, Chongqing 400067, China; 2.National Intelligent Manufacturing Service Site,Chongqing Technology and Business University, Chongqing 400067, China)

Abstract：Porous metal foam magnetorheological fluid damper is a new damper using the foam metal storage of the MRF. By MR damper performance test, we studied the relationship between the damping force and different currents, a magneto-rheological damper forward model is set up by BP neural network. Simulation results show that the neural network model can accurately predict the MR damper damping force and control current, and it also proves the effectiveness of this method. Compared with the existing model, the calculation is simple with high accuracy.

Key words：neural networks; porous foams; magnetorheological fluid; dampers

中图分类号：TB534

文献标志码：A

文章编号：1672-058X(2016)03-0006-04

作者简介：姚行艳(1984-)，女，湖北随州人，讲师，博士，从事振动控制研究.

*基金项目：重庆市教委课题(KJ1500627)；国合基地开放基金(KFJJ201501001).

收稿日期：2015-12-29；修回日期：2016-02-17.

doi:10.16055/j.issn.1672-058X.2016.0003.002