线电荷在无限长矩形腔内激发的电势

李 文 略

(岭南师范学院 基础教育学院，广东 湛江 524037)



线电荷在无限长矩形腔内激发的电势

李 文 略

(岭南师范学院 基础教育学院，广东 湛江 524037)

摘要：线电荷在充满电各向异性介质的无限长矩形腔中激发的电势，是各向异性介质中泊松方程的边值问题；主要应用本征函数法和分离变量法求解了边界条件为第一类齐次和第一类非齐次边界条件时，线电荷在无限长矩形腔内激发的电势；在令ε11=ε22=ε33=ε的情况下，所得的结果可适用于电各向同性介质。

关键词：电各向异性介质；泊松方程；本征函数；分离变量法；δ函数；二重傅里叶级数

关于无限长均匀带电线电荷(简称线电荷)在电各向同性介质中激发的电势的研究很多很深入[1-5]，而关于线电荷在电各向异性介质中激发的电势的研究却很少。陈燊年等人系统地研究了介质为各向异性的电磁场，利用分离变量法有效求解了电各向异性介质中线电荷激发电势的拉普拉斯方程的边值问题[6-7]。文献[8]在文献[6]的基础上应用共形映射法研究了在电各向异性介质(限于有且仅有3个正交主轴方向的电介质)中线电荷与接地平板系统间的电势。此处将继续研究线电荷在矩形腔内激发的电势，求解过程中涉及电各向异性介质中泊松方程的边值问题，可作为求解电各向异性介质中泊松方程边值问题的补充。

1线电荷在无限长接地矩形导体腔内激发的电势

无限长接地矩形导体腔(腔内充满电各向异性介质)沿着电各向异性介质的主轴坐标系O-x1x2x3的x3轴放置(图1)，均匀带电线密度为ρ的线电荷放置在(a/2,b/2)处。

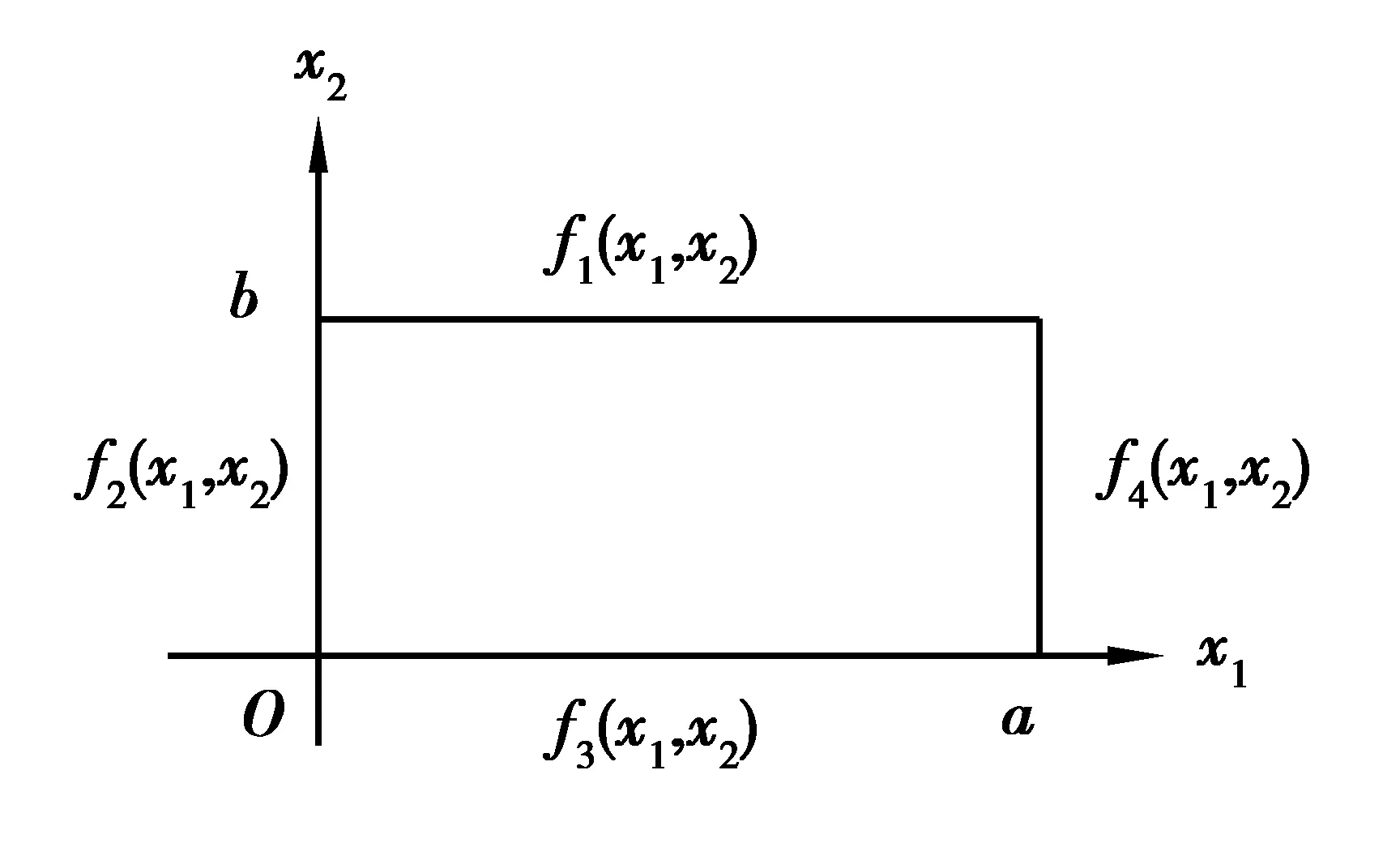
图1　矩形腔截面图Fig.1　Section of rectangular cavity

因接地无限长矩形导体腔内部放置无限长均匀带电线电荷，故腔内的电势与x3无关，线电荷在腔内激发的电势满足电各向异性介质的二维泊松方程的边值问题:

(1)

式(1)中，ε11,ε22分别为沿着x1轴和x2轴正方向的介电常数。

(2)

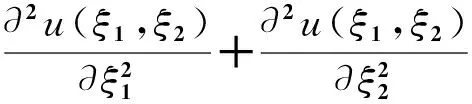
(3)

(4)

将式(4)代入式(2)的泛定方程中，得

(5)

(6)

由δ函数的“筛选”性质，求式(6)的积分可得

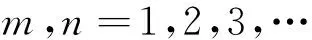
(7)

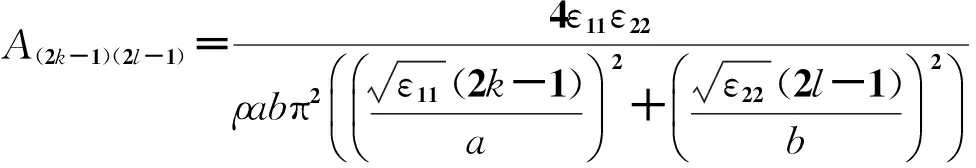
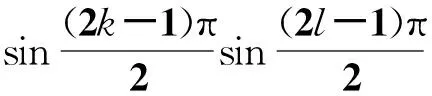
(8)

将式(8)代入式(4)中，可得边值问题式(2)的解为

u(ξ1,ξ2)=

(9)

u(x1,x2)=

(10)即为线电荷在接地无限长矩形导体腔中激发的电势。

若令ε11=ε22=ε33=ε，代入式(10)中，可得线电荷在接地矩形导体腔(腔内充满电各向同性介质)中激发的电势为

2腔的四壁有电势分布时激发的电势

线电荷和无限长矩形腔的放置与前文一样，不同的是腔的四壁有电势分布，该电势分布由第一类非齐次边界条件描述。线电荷在腔内激发的电势满足电各向异性介质的二维泊松方程的边值问题:

(11)

式(11)中，f1(x1,x2)，f2(x1,x2)，f3(x1,x2)和f4(x1,x2)分别为腔四壁电势的空间分布函数。

(12)

为求解边值问题式(12)，先求解边值问题：

(13)

为求解边值问题式(13)，现求解边值问题:

(14)

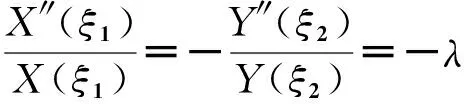
(15)

(16)

λ为分量常数。由边界条件，可得式(15)的本征值和本征函数为

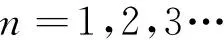
(19)

其中bn为任意常数。将λn代入式(16)中解出Y(ξ2)的通解：

(20)

其中,cn,dn为任意常数。因u1(ξ1,0)=X(ξ1)Y(0)=0，且X(ξ1)≠0，得Y(0)=0，代入式(20)得cn=0，故：

(21)

由式(19)(21)得本征解：

(22)

其中，An=bndn。因式(14)中的泛定方程是线性齐次的，根据叠加原理将本征解叠加在一起，构成一般解：

(23)

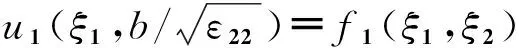
(24)

(25)

式(23)就是边值问题式(14)的一般解，其中系数An由是式(25)确定的。继续求解边值问题：

(26)

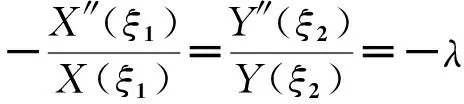
(27)

(28)

λ为分量常数。由边界条件可得式(27)的本征值和本征函数为

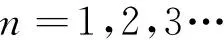
(29)

其中bn为任意常数。将λn代入式(28)中解出X(ξ1)的通解：

(30)

其中cn,dn为不为零的常数(因cn=dn=0，则Xn(ξ1)=0,u2(ξ1,ξ2)=0为平庸解)。

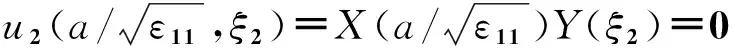
(31)

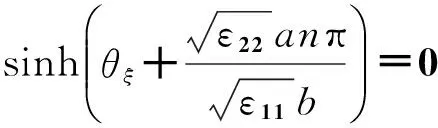
(32)

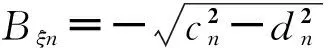
u2n(ξ1,ξ2)=

(33)

其中Bn=bnBξn。因式(26)中的泛定方程是线性齐次的，根据叠加原理将本征解叠加在一起，构成一般解：

u2(ξ1,ξ2)=

(34)

现确定式(34)中的系数Bn。将u2(0,ξ2)=f2(ξ1,ξ2)代入式(34)，得

(35)

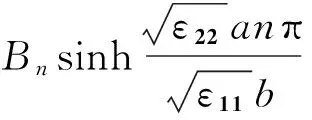
(36)

式(34)就是边值问题式(26)的一般解，其中系数Bn由式(36)确定。

边值问题式(14)与以下的边值问题：

(37)

u4(ξ1,ξ2)=

(38)

(39)

式(38)就是边值问题式(37)的一般解，其中系数Dn由式(39)确定。

边值问题式(26)与以下边值问题：

(40)

u3(ξ1,ξ2)=

(41)

(42)

式(41)就是边值问题式(40)的一般解，其中系数Cn由式(42)确定。

由于边值问题式(13)中泛定方程的线性性质，它的解是边值问题式(14)(26)(37)(40)解的线性和，即

(43)

将式(23)(34)(38)(41)代入式(43)中，可得边值问题式(13)的解：

(44)

其中，展开系数An，Bn，Cn，Dn分别由式(25)(36)(42)(39)确定。

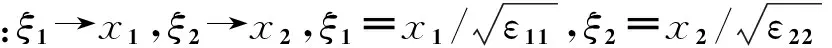
(45)

若令ε11=ε22=ε33=ε，代入式(45)中即可得线电荷在无限长矩形腔(腔内充满电各向同性介质)内激发的电势。

3结语

应用本征函数法和分离变量法求解了线电荷在无限长矩形腔内(腔内充满电各向异性介质)激发的电势，其中本征函数的求解方法可作为现有求解电各向异性介质泊松方程边值问题的补充。线电荷在无限长矩形腔内激发的电势的解析解对工程技术上的利用有一定的参考价值。

参考文献(References)：

[1] 李文略.S-C映射法求线电荷与接地平板系统的电势[J].广西物理，2015,36(1)：38-42

LI W L.The Electric Potential of the Line Charge and the Grounding Plate System by S-C Mapping Method[J].Guangxi Physics，2015,36(1)：38-42

[2] 周凌燕，陈刚，郑洁梅.电像法求解线电荷与带有半圆柱凸起的接地导体所形成的电势和电场[J].大学物理，2013，32(11)：14-16

ZHOU L Y,CHEN G,ZHENG J M.The Image Approach to Solve the Electric Potential of a Line Charged and a Grounded Conductor with the Protruded[J].College Physics，2013,32(11)：14-16

[3] 王福谦.线电荷与带有半圆柱凸起的接地导体所形成的电场[J].大学物理，2010,29(6)：16-17

WANG F Q.The Electric Field of Linear Charges Between Parallel Ground Connection Conduction Plate[J].College Physics，2010,29(6)：16-17

[4] 林焰清，陈刚.线电荷与接地椭圆柱形导体系统的电势[J].大学物理，2009，28(8)：25-27

LIN Y Q.CHEN G.The Electric Potential of a Line Charge and a Cylindroid Conductor System[J].College Physics，2009,28(8)：25-27

[5] 刘润华, 胡先权, 周林,等.导体平板角域内静电场的描述[J].重庆工商大学学报(自然科学版)，2007，24(5):529-532

LIU R H,HU X Q,ZHOU L,et al.Description of Static Electricity Field in Angular Space of Conductor Electrostatics[J].Journal of Chongqing Technology and Business University(Natural Science Edition)，2007,24(5)：529-532

[6] 陈燊年，洪清泉，王建成.介质为各向异性的电磁场[M].北京:科学出版社,2012

CHEN SH N，HONG Q Q，WANG J CH.Electromagnetic Field for the Anisotropic Medium[M].Beijing:Sciencs Press, 2012

[7] 苏武浔，陈芳，陈燊年.各向异性介质静电势微分方程的分离变量法[J].华侨大学学报(自然科学版)1997，18(1):87-92

SU W X,CHEN F,CHEN SH N.Separation of Variable for Solving Differential Equations of Electrostatic Potential in Anisotropic Medium[J].Journal of Huaqiao University(Natural Science Edition)，1997,18(1)：87-92

[8] 李文略.共形映射法求无限长带电直导线的电势[J].广西物理，2014，35(3):17-21

LI W L.Conformal Mapping Method for the Calculation of the Potential of an Infinitely Long Charged Straight Wire[J].Guangxi Physics，2014,35(3)：17-21

责任编辑：李翠薇

The Electric Potential of a Line Charge in an Infinitely Long Rectangular Cavity

LI Wen-lue

(College of Basic Education，Institute of Lingnan Normal University，Guangdong Zhanjiang 524037，China)

Abstract：The electric potential of linear charge in an infinite rectangular cavity filled with anisotropic dielectric is the boundary value problem of Poisson equation in anisotropic media. The electric potential of linear charge in the infinite rectangular cavity is solved by using method of eigenfunction and method of separation of variables,when the walls of the cavity meet the first homogeneous boundary conditions or meet the first nonhomogeneous boundary conditions. The results can apply to isotropic dielectric in the situation: ε11=ε22=ε33=ε.

Key words:anisotropic dielectric；Poisson equation；eigenfunction；method of separation of variables；δ Function；double Fourier series

中图分类号：O441.4

文献标志码：A

文章编号：1672-058X(2016)03-0022-006

作者简介：李文略(1981-)，男，广东茂名人，讲师，从事张量分析和电磁场理论研究.

收稿日期：2015-10-31；修回日期：2015-11-30.

doi:10.16055/j.issn.1672-058X.2016.0003.005