哈弗斯皮质骨径向直裂纹研究

闫伟文, 赵雁楠

(山西工商学院 基础教学部,太原 030006)



哈弗斯皮质骨径向直裂纹研究

闫伟文, 赵雁楠

(山西工商学院 基础教学部,太原 030006)

摘要：哈弗斯皮质骨的断裂微观力学已被提出，在骨中由于疲劳负荷和循环载荷形成微裂纹，有研究者利用二维力学纤维陶瓷基复合材料模型，针对间骨板中出现任一径向直线裂纹的问题，研究了骨单位与裂纹间的相互作用；为更真实模拟骨裂纹的情形，研究了骨单位和间骨板中同时出现一条直线裂纹的情况，通过将裂纹看作一系列连续韧性位错的塞积群，运用格林函数转化为一系列奇异积分方程，然后通过Erdogon和Gupta方法求解方程，并用高斯-切比雪夫数值离散求得相应的应力强度因子，分析对骨微结构形态的影响。

关键词：哈弗斯皮质骨；微裂纹；刃型位错；奇异积分方程；应力强度因子

1简介

骨在疲劳载荷和循环载荷条件下,会发生微断裂形成微裂纹[1-2],微裂纹的形成和扩展与骨微结构密切相关[3]。人类的哈弗斯皮质骨被看作纤维陶瓷基复合材料模型[4],骨单位被看作复合材料的纤维,间骨板被看作复合材料的基,骨单位与间骨板之间通过粘合线被完美结合在一起。在陶瓷纤维基复合材料模型的基础上,学者们研究了骨单位与间骨板中单一直裂纹相互影响的微结构形态[5-7]。此处研究骨单位和间骨板中同时出现一条x轴径向直裂纹的情形,基于线弹性断裂力学基本理论,通过引入格林函数,采用刃型位错方法将问题转化为一系列柯西核的奇异积分方程,并用高斯-切比雪夫数值离散方法求得微裂纹尖端的应力强度因子,分析当骨单位和间骨板中同时出现微裂纹时,它们之间的相互作用对骨微结构断裂的影响。

2问题与表述

研究的物理问题如图1，线性裂纹同时出现在骨单位和无限大的间骨板中，裂纹与附近的骨单位嵌在间骨板中。假设哈弗斯系统是均匀的，骨单位和间骨板完美结合在一起，忽略骨单位间的相互作用，只考虑一个骨单位与裂纹间的相互作用，排除粘合线的干扰，裂纹位于x轴上且沿骨单位径向，整个组织被认为是平面应力状态。

在图1中，以骨单位的中心为原点建立直角坐标系，横坐标表示裂纹长度，单位为微米(μm)；纵坐标表示骨组织所受的单轴应力，单位为牛(N)。间骨板(phase1)有弹性特征G1(Pa)和K1，骨单位(phase2)有弹性特征G2(Pa)和K2(其中Ki=3-4vi，vi为泊松比，Gi为剪切模量,Gi=Ei/2(1-vi),Ei为弹性模量,i=1,2)；骨单位半径长R0(μm)；间骨板中微裂纹长为L1(μm)，裂纹左端点为

a1,右端点为b1；骨单位中微裂纹长为L2(μm)，裂纹左端点为a2,右端点为b2；间骨板中裂纹中心距骨单位中心的距离为d(μm)；骨单位中裂纹中心距骨单位中心的距离为e(μm)；哈弗斯系统在无穷远处受到一个Y轴拉应力σ0(N)。

图1　哈弗斯皮质骨模型Fig.1　Osteon-interstitial tissue model

裂纹问题的边界条件如下：

① 哈弗斯系统受到Y轴拉应力为常数：σ0=常数。

② 在骨单位phase2与间骨板phase1中，X轴所受拉应力σrr与径向受到的拉应力σrθ均为0：

③ 骨中心裂纹上任意点受到的Y轴张应力为σ2yy，X轴向上拉应力σ2xy；间骨板裂纹上任意点受到的Y轴张应力σ1yy，X轴向上拉应力σ1xy：

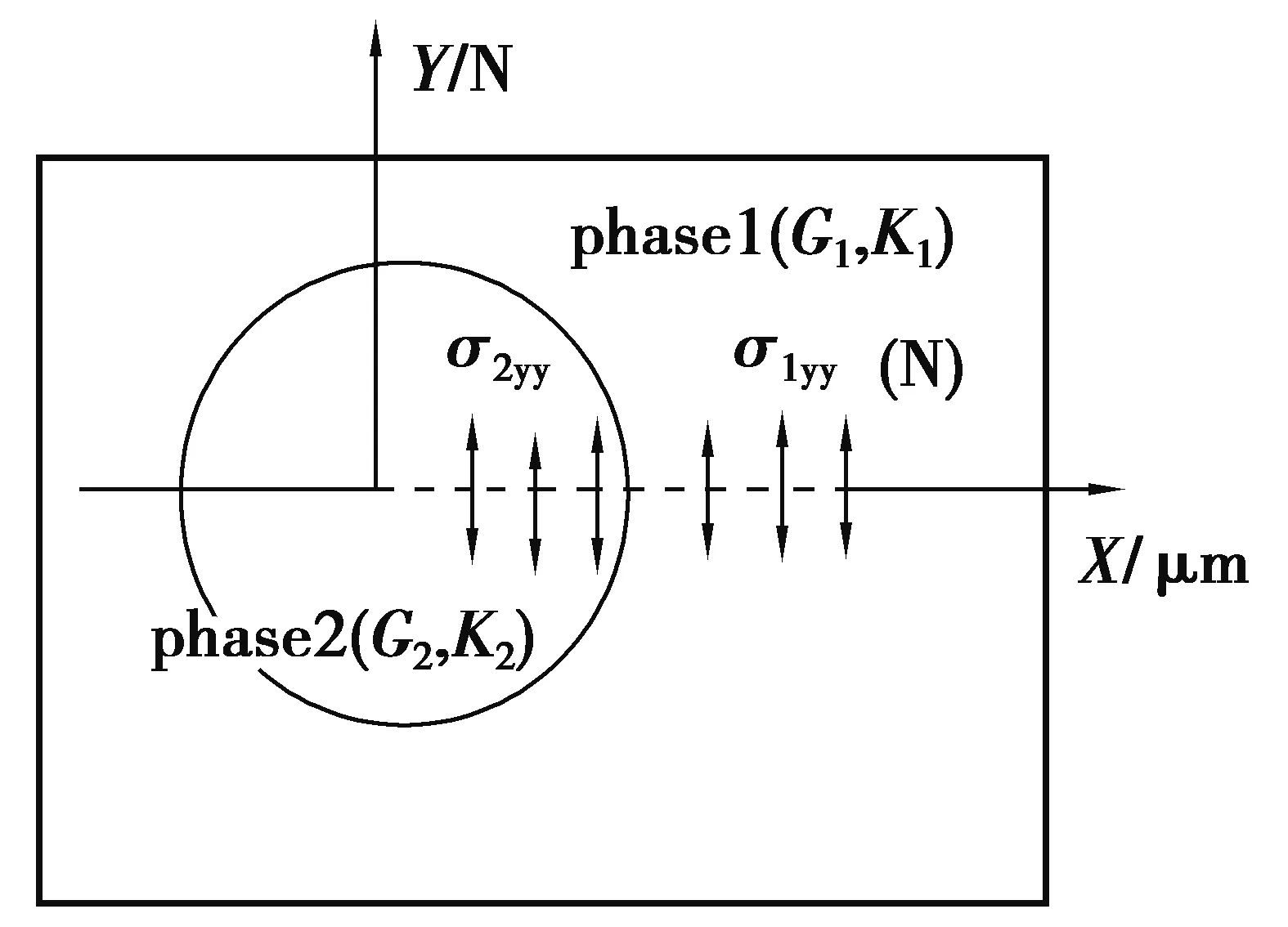
图2　子问题一Fig.2　Subproblem One

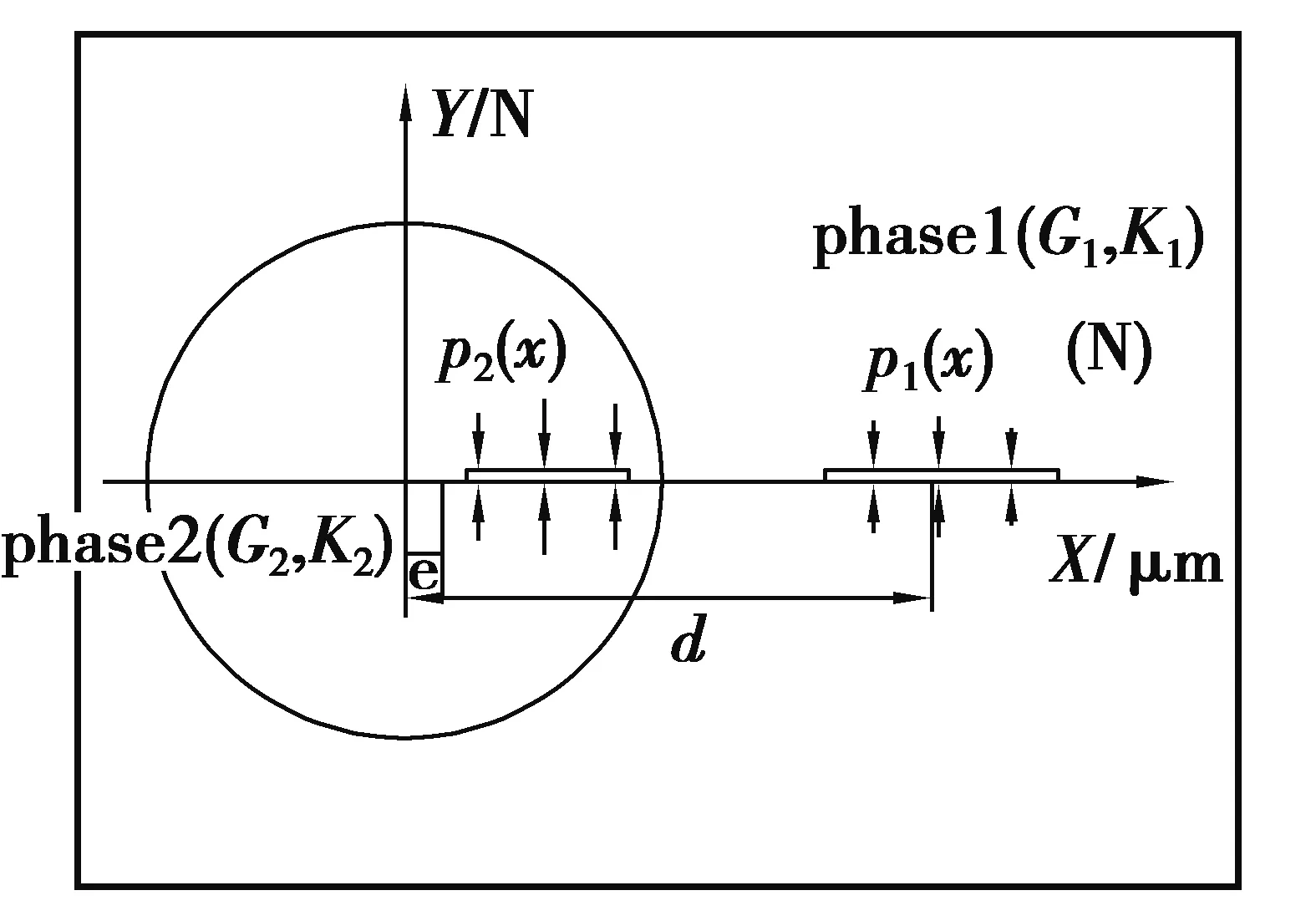
图3　子问题二Fig.3　Subproblem Two

为了将远场问题转变到裂纹表面上,图1的原始问题被分解为图2和图3的两个子问题，一个弹性骨单位位于无限大的弹性平面—间骨板中。子问题一如图2所示，间骨板没有任何微裂纹，图中虚线表示原来微裂纹的位置，哈弗斯系统在远场受外载荷0，间骨板虚裂纹处受Y轴张应力为σ1yy(x)，骨单位虚裂纹处受Y轴张应力为σ2yy(x)。子问题二如图3所示，哈弗斯系统在远场受外载荷0，在骨单位和间骨板中同时存在微裂纹，间骨板微裂纹处受Y轴张应力为p1(x)，骨单位微裂纹处受Y轴张应力为p2(x)，子问题一，子问题二的叠加就是原始问题。

子问题一中虚裂纹处受到的张应力为[8]

(1)

(2)

(3)

(4)

(5)

3模型求解

运用刃型位错[9]、格林函数求解[8]，得到如下奇异积分方程：

其中，

4数值求解过程

由于裂纹尖端会出现1/2阶的奇异性，则令

(8)

这里F1y(x)为a1≤x≤b1上的有界函数，F2y(x)为a2≤x≤b2上的有界函数，且

(9)

下面将裂纹区间(a1,b1),(a2,b2)转化到(-1,1)上，则令

(10)

按照上述变换，将方程(6)(7)中的变量替换为u,v，根据积分方程[10]数值离散，得到I型裂纹尖端的应力强度因子[11],外部裂纹的记为K11,内部裂纹的记为K12：

5数值结果与分析

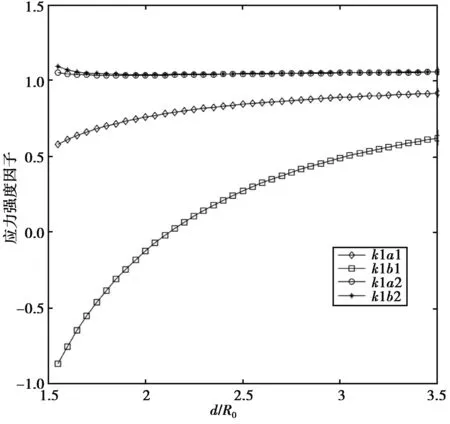
图4　裂纹尖端a,b标准应力强度因子(G2/G1=0.5)Fig.4　The normalized SIF of microcrack tips(a) and (b)(G2/G1=0.5)

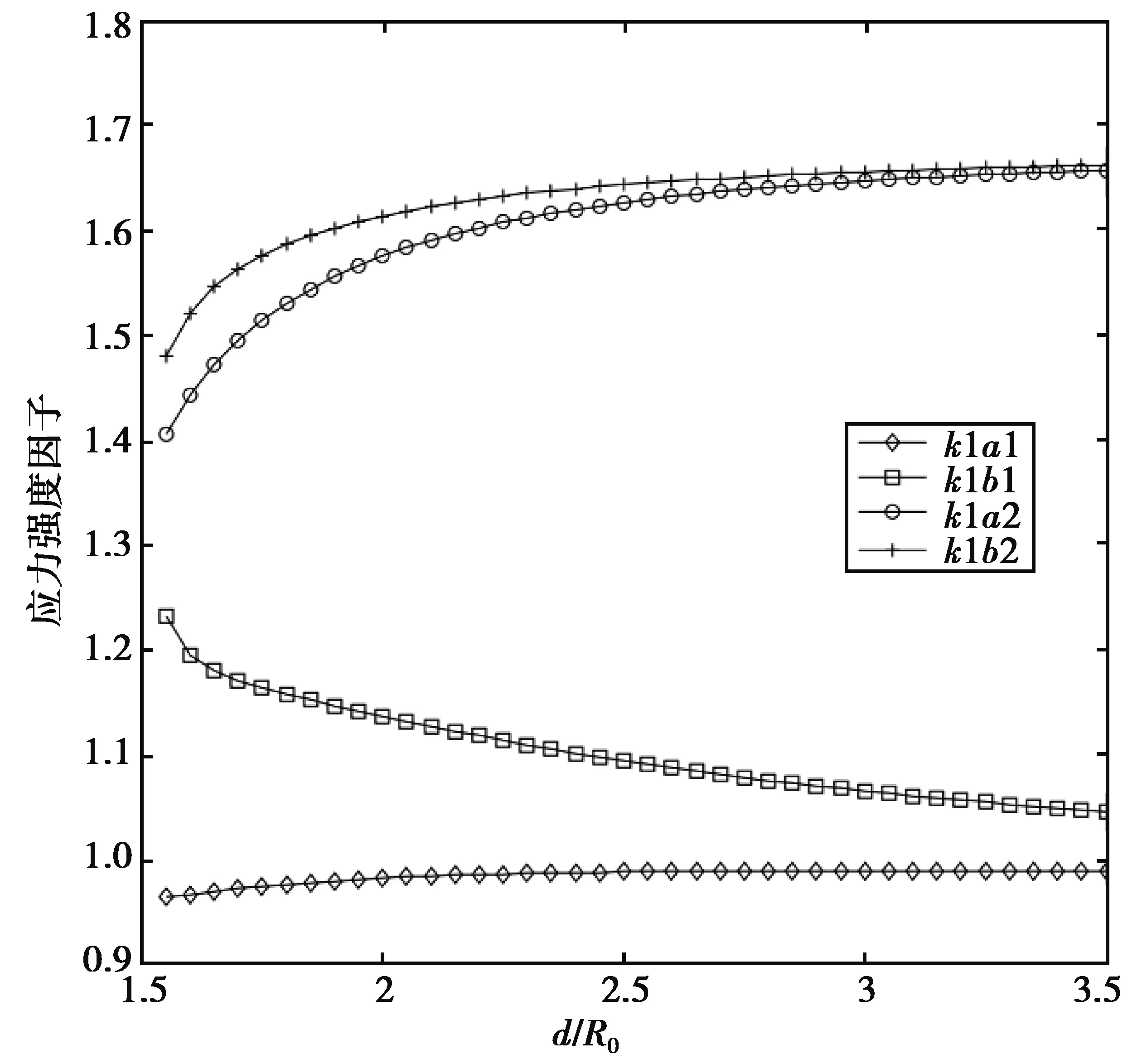
图5　裂纹尖端a,b标准应力强度因子(G2/G1=2)Fig.5　The normalized SIF of microcrack tips(a) and (b)(G2/G1=2)

图6，图7横坐标表示标准距离e/R0，纵坐标表示裂纹尖端的应力强度因子。图6中针对软骨组织(G2/G1=0.5),间骨板中裂纹a1端的应力强度因子k1a1随着e的增大几乎不变，间骨板中裂纹b1端的应力强度因子k1b1随着e的增大先急剧增大后趋于不变，骨单位中裂纹a2与b2端的应力强度因子k1a2和k1b2随着e的增大几乎不变。分析图6的数值结果，哈氏皮质骨的骨单位对附近直裂纹的断裂韧性存在影响。当骨单位弹性模量小于间骨板的弹性模量时，裂纹的断裂韧性被增强。图7中针对硬骨组织(G2/G1=2),间骨板中裂纹a1端的应力强度因子k1a1和骨单位中裂纹b2端的应力强度因子k1b2随着e的增大几乎不变，间骨板中裂纹b1端的应力强度因子k1b1随着e的增大先急速下降后趋于不变，骨单位中裂纹a2端的应力强度因子k1a2随着e的增大先不变后急剧下降。分析图7的数值结果，骨单位的弹性模量大于间骨板的弹性模量时，裂纹的断裂韧性被削弱，这样的结构同样说明骨骼整体的抗断裂性能达到最优。

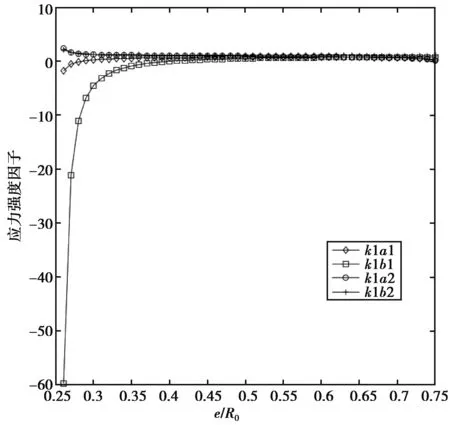
图6　裂纹尖端a,b标准应力强度因子(G2/G1=0.5)Fig.6　The normalized SIF of microcrack tips(a) and (b)(G2/G1=0.5)

6结论

实验结果表明，骨单位与间骨板间的微结构力学特征跟年龄、疾病、基因等因素有关[13-14]。不同年龄段的骨组织力学特征可能差距很大，老年人在骨受一定载荷条件下比年轻人更易断裂，即使年龄一样大，身体素质好的人要比身体素质差的人的骨更能经受住抗力。文章的结果表明，当骨单位弹性模量小于间骨板弹性模量时,内外裂纹的断裂韧性被增强。反之，骨单位的弹性模量大于间骨板的弹性模量时,内外裂纹的断裂韧性被削弱。这样的结构使得骨骼整体的抗断裂性能达到最优，随着两裂纹距离的逐渐增大，内外两端的应力强度因子会增大或减小。此处分析骨的微断裂行为，通过数值算例考虑骨单位及微裂纹之间的相互影响，模型及使用方法简单易行，有望后人会提出更切合实际的模型来模拟真实骨组织，以备用于实际临床研究。

参考文献(References)：

[1] MARTIN R B.Mathematical Model for Repair of Fatigue Damage and Stress Fracture in Osteonal Bone[J].Journal of Orthopaedic Research,1995,13(3)：309-316

[2] HERMAN B C,CARDOSO L,MAJESKA R J,et al.Activ-ation of Bone Remodeling After Fatigue：Differential Response to Linear Microcracks and Diffuse Damage[J].Bone,2010,47(4)：766-772

[3] BAJAJ D,GEISSLER J R,ALLEN M R,et al.The Resistance of Cortical Bone Tissue to Failure Under Cyclic Loading is Reduced with Alendronate[J].Bone,2014,64(7)：57-64

[4] PRENDERGAST P J,HUISKES R.Microdamage and Osteocyte-lacuna Strain in Bone：A Microstructural Finite Element Analysis[J].Journal of Biomechanical Engineering,1996,118(2)：240-246

[5] NAJAFI A R,ARSHI A R,ESLAMI M R,et al.Micromechanics Fracture in Osteonal Cortical Bone：A Study of the Interactions between Microcrack Propagation,Microstructure and the Material Properities[J].Journal of Biomechanics,2007,40(12)：2788-2795

[6] NAJAFI A R,ARSHI A R,ESLAMI M R,et al.Haversian Cortical Bone Model with Many Radial Microcracks：an Elastic Solution[J].Medical Engineering and Physics,2007,29(6)：708-717

[7] NAJAFI A R,ARSHI A R,ESLAMI M R,et al.A Fiber-ceramic Matrix Composite Material Model for Osteonal Cortical Bone Fracture Micromechanics：Solution of Arbitrary Microcracks Interaction[J].Journal of The Mechanical Behavior of Biomedical Materials,2009(3)：217-223

[8] ERDOGAN F,GUPTA G D,RATWANI M.Interaction between a Circular Inclusion and an Arbitrarily Oriented Crack[J].Journal of Applied Mechanics,1974,41(3)：1007-1013

[9] DUNDURS J,MURA T.Interaction Between an Edge Dislocation and a Circular Inclusion[J].Journal of The Mechanics and Physics of Solids,1964,12(3)：177-189

[10] 李星.积分方程[M].北京：科学出版社,2008

LI X.Integral Equation[M].Beijing:Science Press,2008

[11] HILLS D A,KELLY P A,DAI D N,et al.Solution of Crack Problems：the Distributed Dislotion Technique[J].Journal of Applied Mechanics,1998,65(2)：548-550

[12] SEREF-FERLENGUEZ Z,BASTA-PIJAKIC J,KENNEDY OD,et al.Structural and Mechanical Repair of Diffuse Damage in Cortical Bone in Vivo[J].The Official Journal of the American Society for Bone & Mineral Research,2014,29(12)：2537-2544

[13] DOBLARE M,GARCIA J M,GOMEZ M J.Modeling Bone Tissue Fracture and Healing：a Review Eng Fractmech[J].Engineering Fracture Mechanics,2004,71(13-14)：1809-1840

[14] URAL A,JANEIRO C,KARIM L,et al.Association between Non-enzymatic Glycation,Resorption,and Microdamage in Human Tibial Cortices[J].Osteoporos Int,2015,26(3)：865-873

责任编辑：李翠薇

Research on Radial Vertical Rupture of Haversion Cortical Bone

YAN Wei-wen, ZHAO Yan-nan

(Department of Basic Knowledge Teaching, Shanxi Technology and Business College, Taiyuan 030006, China)

Abstract：The micromechanics of the rupture of Haversion cortical bone has been pointed out, the microcracks form in Haversion cortical bone owing to fatigue load and cyclic load. Based on two-dimensional micromechanical fibre-ceramic matrix composite tissue material model, some researchers study the interaction between osteon and their cracks according to any radial vertical rupture in interstitial lamella. In order to more practical simulate bone rupture, this paper mainly studies that a straight line rupture simultaneously appears in osteon and inter-bone lamella, regards cracks as a series of continuous edge dislocation pile-up group, then uses Green function to transform them into a series of singular integral equations, then uses Erdogon and Gupta method to solve the equations, uses Gaussian-Chebyshev numerical discrete method to obtain corresponding stress intensity factor and analyzes the influence on bone microstructure morphology.

Key words：Haversion cortical bone; microcrack; edge dislocation; singular integral equation; stress intensity factor

中图分类号：TB122

文献标志码：A

文章编号：1672-058X(2016)03-0028-06

作者简介：闫伟文(1986-)，女，山西朔州人，硕士，助教，从事复分析在力学上的应用研究.

收稿日期：2016-01-06；修回日期：2016-02-10.

doi:10.16055/j.issn.1672-058X.2016.0003.006