面向航空复杂薄壁零件智能加工的进化建模方法*

（西北工业大学现代设计与集成制造技术教育部重点实验室，西安 710072）

目前，航空发动机关键零件加工存在精度低和质量稳定性差等问题，严重制约了我国航空发动机技术的发展[1]。由于材料难加工、结构复杂、壁厚很薄，发动机关键零件在加工过程中产生伴随材料切除的非线性、强时变问题（零件几何与动力学变化以及刀具的快速磨损等现象）。采用现有的方法难以对该类零件的加工过程进行精确的建模，只能简化表征，从而限制了模型的精度和预测能力[2]。

本文针对复杂薄壁零件加工过程非线性、强时变的建模问题，提出了基于时域离散的加工过程多态演化模型，给出了多态模型的演化机制，并建立了零件几何演化模型、零件动力学演化模型、刀具磨损演化模型以及加工误差补偿进化模型。以机匣和叶片为例，通过仿真和试验方法验证了多态演化模型及进化建模方法的可行性。

加工过程的多态演化模型

加工过程的多态演化模型是加工过程的时域离散表示，包括多态模型和演化模型。多态模型是离散时间序列上的加工过程状态集合。演化模型是实现多态模型中相邻状态之间转移的子过程。通过时域离散，可将非线性时变过程转化为局部的线性定常过程进行建模和求解。

1 加工过程的时域离散方法

以发动机机匣为例，设其在时域[0,T]内的加工过程状态为{St=S(t)|0＜t＜T，S0=S(0)}，则其时域离散和多态演化模型定义方法如图1所示。

（1）从机匣毛坯到成品的加工过程可划分为粗加工、半精加工、精加工和抛光等工序。因此，工序多态模型可定义为各工序开始时刻{tk、|tk＜t(k+1)(k=0,1,…,n-1) }的状态集合{Sk=S(tk)}，而工序演化模型则定义为相邻工序状态间的转移子过程集合 {Mk=St-Sk|tk＜t≤tk+1}。

（2）工序演化模型Mk可在时域[tk,tk+1]内离散为时间序列{tk,j|tk,j＜tk,j+1(j=0,1,…,m-1)}上的工步状态集合{Sk,j}，以及相邻工步状态（Sk,j和Sk,j+1）之间的转移子过程集合{Mk,j}。

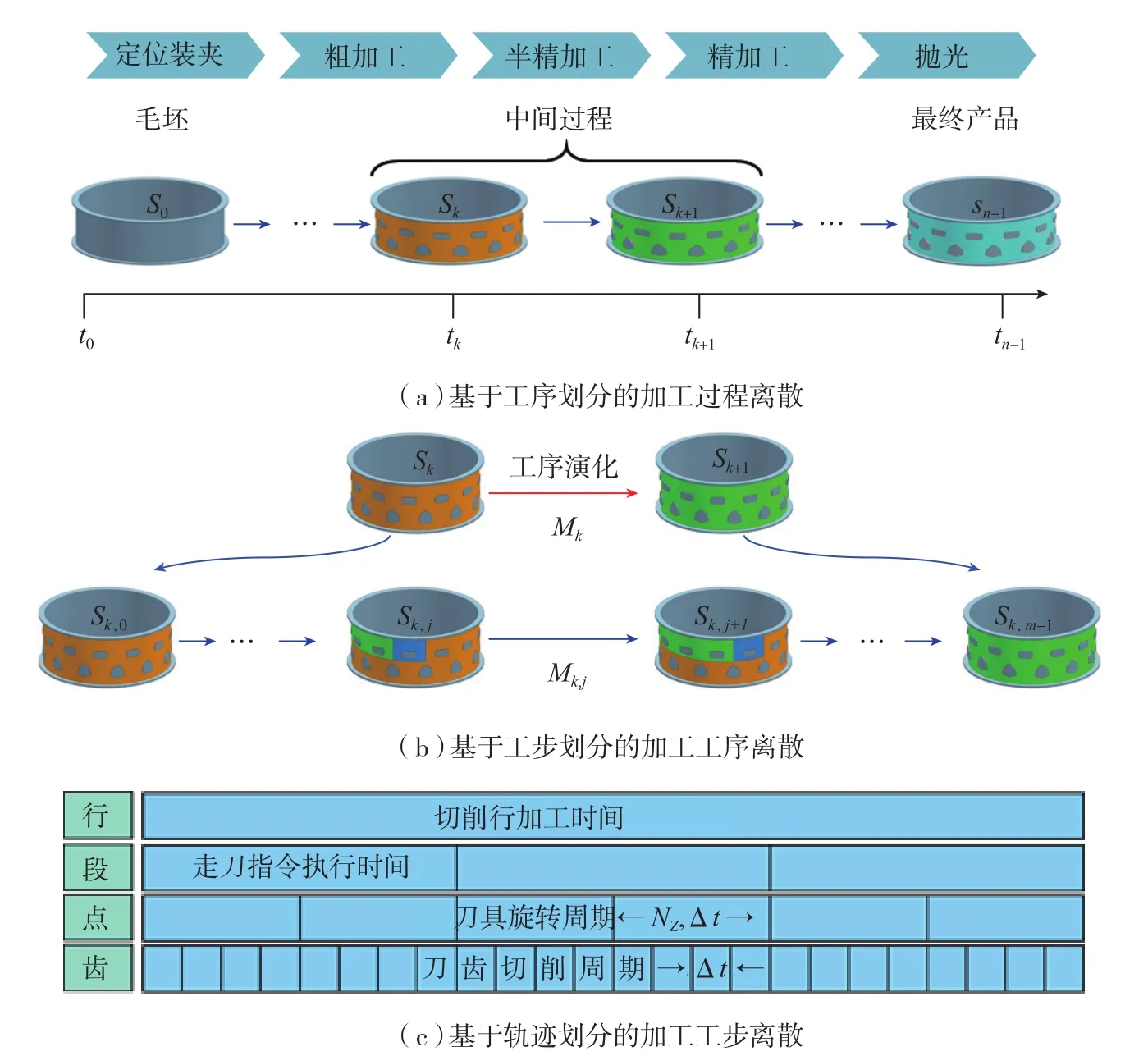
图1 加工过程的时域离散方法Fig.1 Discrete time domain method of machining process

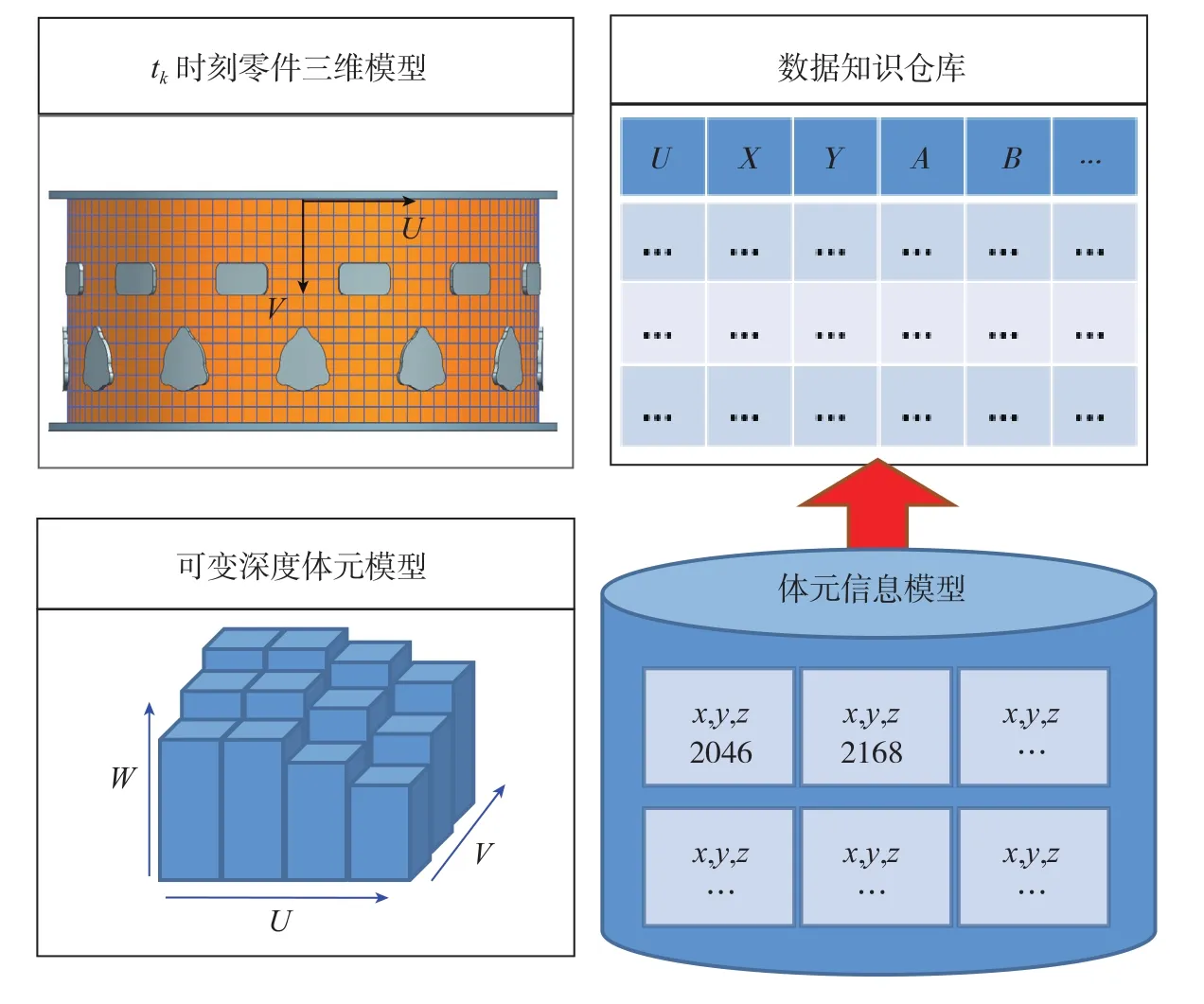
图2 状态模型Sk的表示方法Fig.2 Express of state model Sk

（3）第j工步的演化模型Mk,j由加工轨迹和切削参数定义，并通过相邻工步间余量切除过程实现。其中，加工轨迹由若干个切削行连接组成。通过分层次时域离散，可将切削行细分为切削段、刀位点、直到刀齿切削过程。而刀齿切削周期内的切削过程建模和求解，可利用现有切削几何、力学和物理模型及其时域离散算法实现。

2 多态模型的定义方法

如图2所示，第k工序开始时刻的状态模型Sk中包括该状态下的三维几何模型和信息模型。其中三维几何模型采用三维变形曲面实体的空间离散方法表示，包含UVW参数空间中的可变深度体元、XYZ物理空间中的曲面实体以及两者间的空间映射关系，可以表示为:[x,y,z]=[x(u,v,w),y(u,v,w),z(u,v,w)]。

信息模型由附加在体元上的信息单元和数据知识仓库组成。每个信息单元通过体元位置编码与数据知识仓库关联，实现体元位置相关的工艺知识表示、存储和处理。数据知识仓库用于记录现场数据和体元位置相关的工艺知识。现场数据包括体元位置、加工过程信号及其时空映射关系。体元位置相关的工艺知识包括现有工艺知识和现场数据挖掘处理得到知识，如局部观测模型Y=AX+BU中的输入向量U、状态向量X、输出向量Y、模型参数A,B的辨识结果，以及局部模态刚度、模态频率等动态响应特性参数。

演化模型的实现方法

演化模型的实现方法主要涉及与余量切除过程相关的零件几何与动力学变化，以及刀具磨损等现象的建模和求解方法。

1 零件几何演化模型

零件几何演化模型通过定义相邻工步之间的余量实体及其切除顺序，可更精确地描述零件过渡表面的形状及其在切削过程中的变化。

如图3所示，余量实体在参数空间中表示为变深度体元模型D={D(ui,vj,w)}。变深度体元在零件表面上的位置参数为[ui,vj]，深度参数为w且在[0,1]范围内可变，深度变化过程用体元切除顺序表示为p(t)=(u(t),v(t))。

余量实体在物理空间中表示为曲面实体模型S(u,v,w)。若{wk=w(tk)|tk-1＜tk(k=0,1,…,n-1)}为对应于不同工步的深度参数划分，则利用参数空间到物理空间的曲面实体变形映射可自动生成不同切削深度的过渡面族[3]。基于tk时刻状态模型Sk的过渡面S(u,v,wk)，可计算当前加工余量的分布，并在该过渡面上生成刀具轨迹c(t)，作为后续动力学演化分析的输入。

在实际加工中，相邻过渡面的切削深度变化必须满足工艺余量分布约束。为此，文献[4]通过拉格朗日插值引入虚拟控制面，实现了考虑工艺约束的过渡面余量分布控制。如图4所示，通过在毛坯表面S0和零件表面S1之间插入虚拟控制面S2和S3，可有效控制过渡面的变形速度分布，使过渡面变得更加光滑，余量分布更为均匀。

2 零件动力学演化模型

零件动力学演化模型定义余量切除过程中零件动力学特性的变化。图5所示为第k工序中相邻工步状态Sk,j和Sk,j+1间的动力学演化建模与求解过程。其输入为当前工步S(k,j)的体元深度和切除顺序，可采用结构动力修改方法进行求解[5-7]。

整个求解过程包括结构动力修改、动力学建模、动态响应预测和参数控制窗口选取等4步：

（1）结构动力修改：当第i个切削段中的体元余量被切除后，将零件的模态质量和模态刚度修改为Mk,j,i=Mk,j,i-1-ΔMk,j,i，Kk,j,i=Kk,j,i-1-ΔKk,j,i，并预测零件模态参数随材料切除的演化规律。

（2）动力学建模：机匣的环形、薄壁结构特征使得零件的主模态沿零件表面法向进行分布，因此可以建立只考虑零件表面法向的一维颤振稳定性模型：

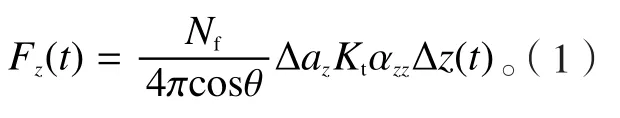
（3）动态响应预测：通过求解动态响应方程，可预测下一切削段的稳定性极限alim、主轴转速n等加工稳定性参数：

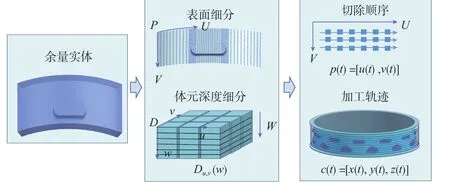
图3 零件几何演化模型定义Fig.3 Definition of work piece geometry evolution model

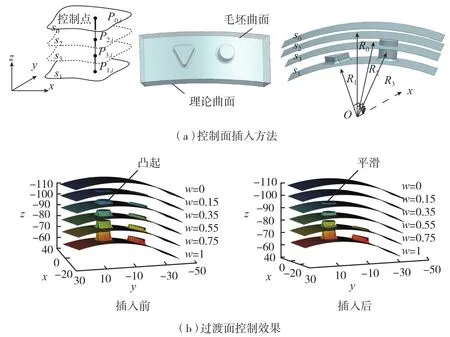
图4 加工余量变化控制方法Fig.4 Control method of process allowance

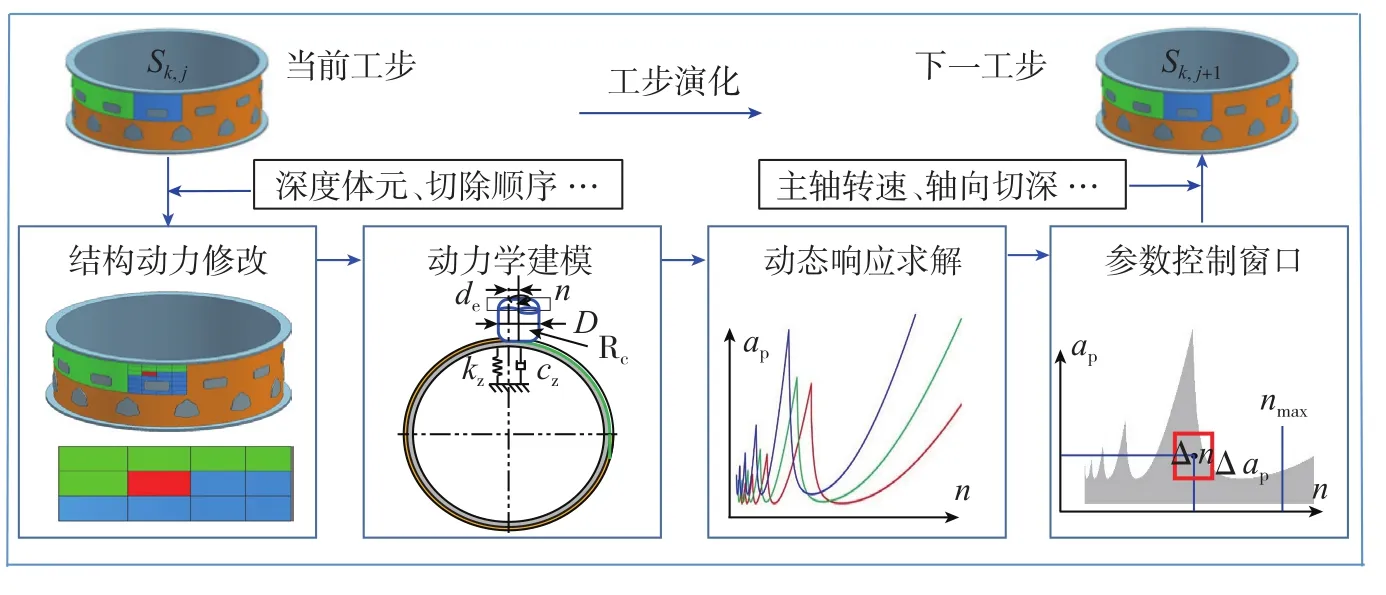
图5 工步演化过程的动力学建模与求解Fig.5 Modeling and calculation of work piece dynamics during step evolution

（4）选取参数控制窗口，根据相应计算结果选取适合下一切削段的加工参数（切深和转速），从而保证了整个加工工序的稳定切削。

图6为机匣加工过程的动力学特性计算结果。图中曲线分别表示固有频率和法向刚度在同一个切削行内随材料切除而下降的规律。彩色云图表示整个切削过程，法向刚度在整个u,v参数空间中的分布。从中可以看出，不同工步之间零件的动力学特性差异较大，无法使用固定的参数（主轴转速、进给速度）保证一个工序内的持续稳定切削，需要在加工过程中逐步调整。

3 刀具磨损演化模型

刀具后刀面磨损是航空难加工材料零件切削过程中的强时变因素。当刀具磨损量达到一定限度后，将严重影响切削力热耦合作用以及加工表面质量。因此，建立刀具磨损演化模型在加工过程中实时监测刀具磨损状态极为重要。

文献[8]根据刀具分阶段磨损规律，以后刀面磨损量、磨损速度为状态参数，建立了刀具磨损的多态模型：

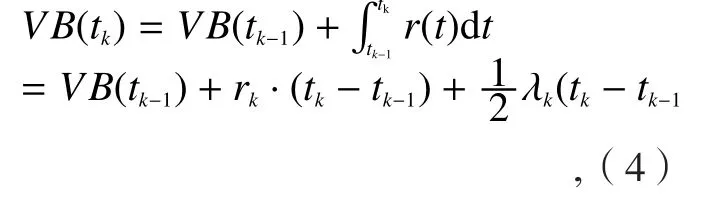
公式（4）中，tk≤t≤tk+1，VB(tk)时刻刀具总的磨损量，rk为tk时刻的刀具磨损率，λk为tk时刻刀具磨损加速度。

根据刀具三阶段磨损规律，公式（4）在刀具磨损的3个阶段可以分别表示，如图7所示。

（1）初期磨损阶段：该阶段刀具磨损量为时间的二次曲线，可以表示为：

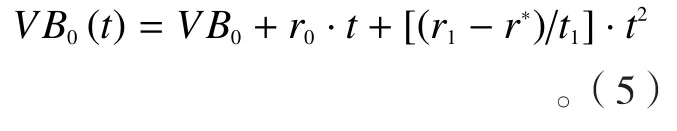
（2）正常磨损阶段：该阶段刀具磨损量与时间成线性关系，可表示为：

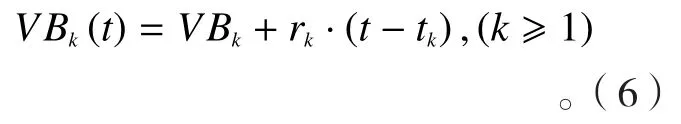
在加工过程中，设置刀具磨损的侦测识别监测点，通过监测和计算可获得tk时刻的刀具磨损量VBk和磨损率rk，利用公式（6）实现t＞tk时的刀具磨损量VBk(t)的预测。

（3）急剧磨损阶段：当监测结果出现rk＞rmax或λk＞ε或VBk≥VBmax时，刀具进入急剧磨损阶段，并触发停止加工、更换刀具指令。

在确定的工况条件下，公式中rk和VBk为切削速度Vc和每齿进给量fz的函数，可以通过试验方法建模。图8中的（a）和（b）分别为通过试验获得的t1时刻的刀具磨损率r1和后刀面磨损量VB1随切削速度vc和每齿进给量fz的变化关系。

在真实零件铣削过程中，可采用侦测加工技术在线识别刀具磨损量。当需要识别刀具磨损量时，通过数控系统主动给每齿进给量fz叠加1个激励增量Δfz，使得实际的每齿进给量为fz+Δfz。根据铣削力监测信号，计算出激励前后的平均铣削力结合切削力方程即可求解出特定时刻的后刀面磨损量VB值[9]。

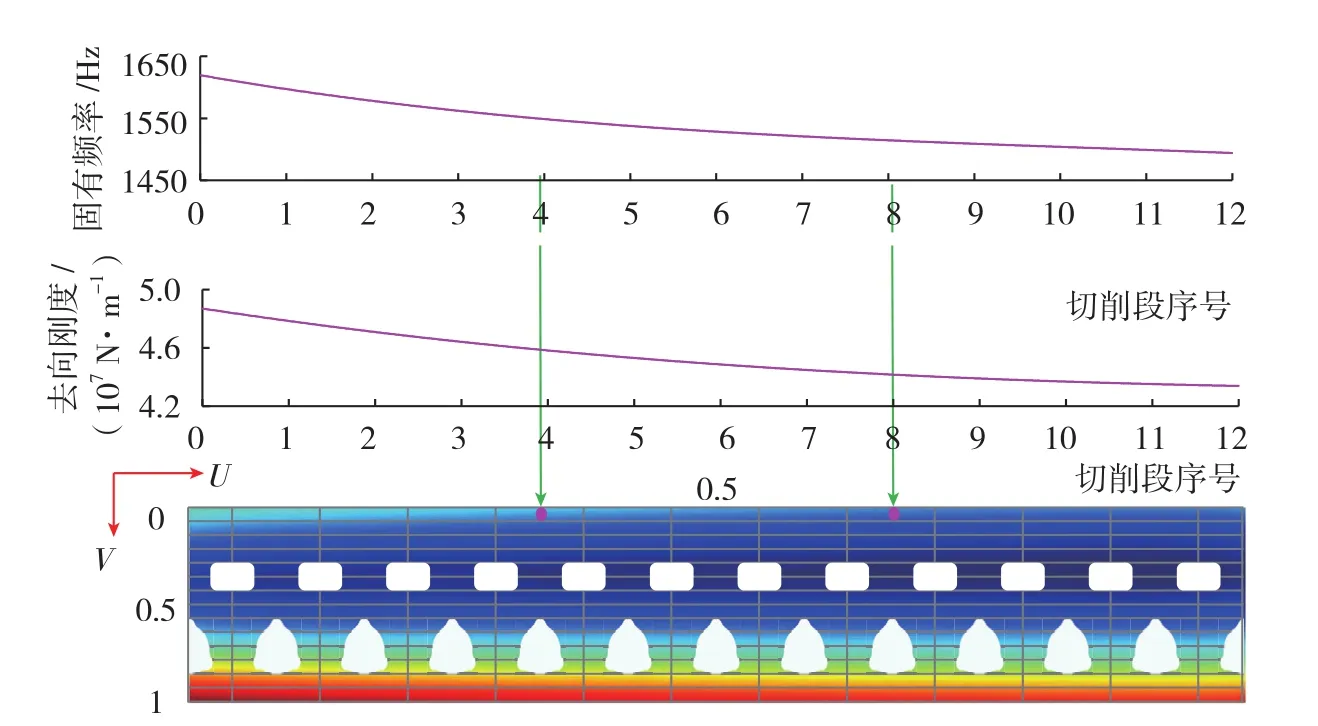
图6 机匣动力学特性变化图Fig.6 Variation of casing dynamics

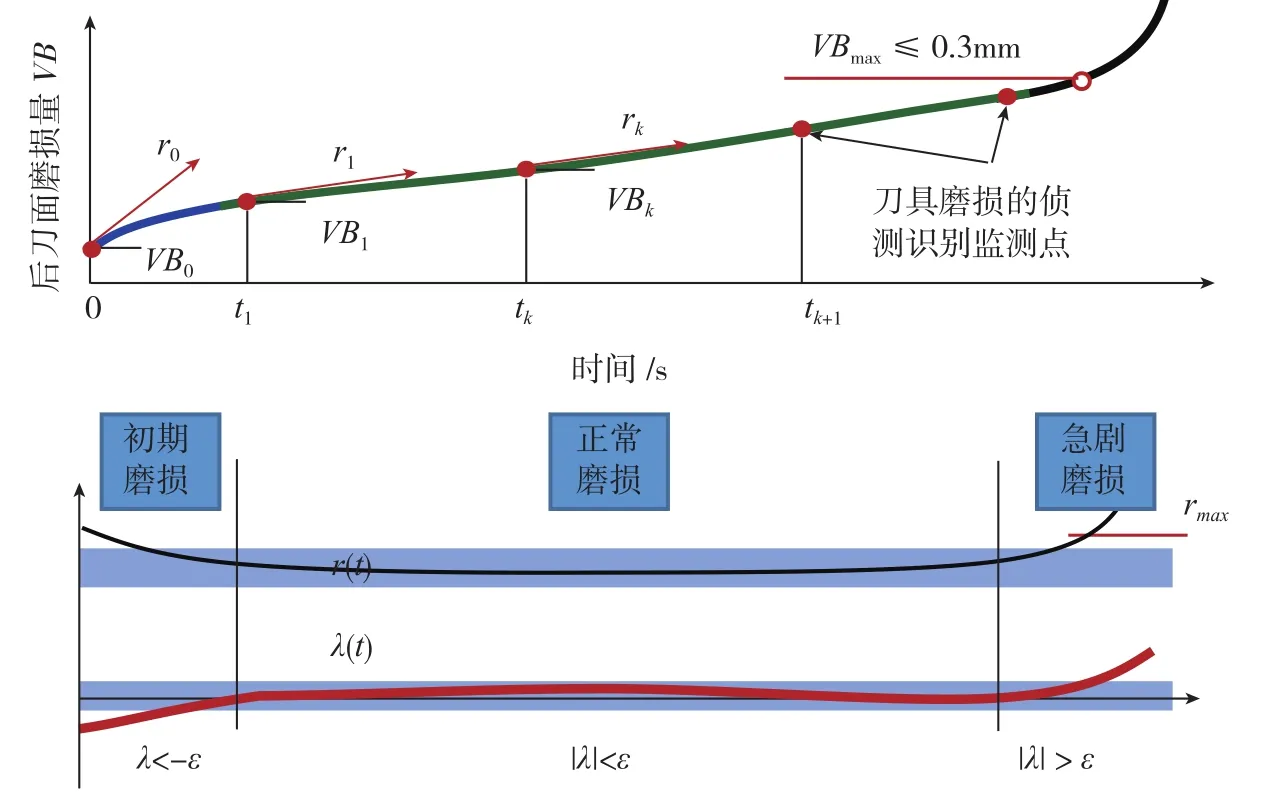
图7 刀具磨损量监测与控制示意图Fig.7 Monitoring and control of tool wear

与此同时，还可侦测加工技术对其他工况参数进行辨识，以获得实际工况的影响因素，及时修改磨损率模型。当检测到刀具进入急剧磨损阶段后系统即时发出报警并更换刀具，以免发生不必要的损失。

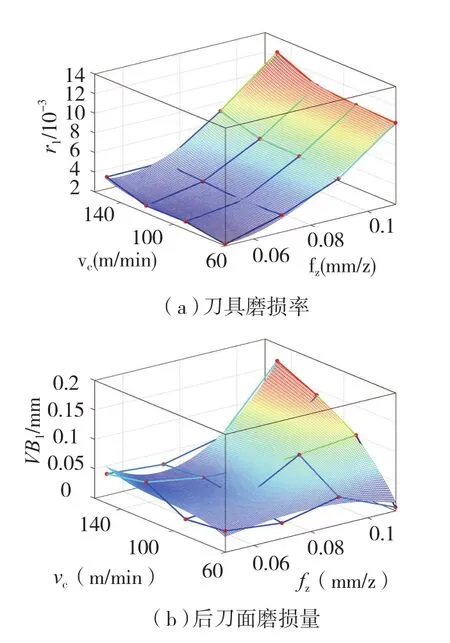
图8 刀具磨损试验建模Fig.8 Tool wear experiments

加工综合误差补偿进化模型

加工综合误差主要包括机床原始误差、切削力/切削热引起的变形误差、刀具磨损引起的误差、机床特性改变等引起的积累误差，最终全部表现在刀具与零件的交互界面上，使零件产生动态的尺寸误差。薄壁零件加工的弹性让刀和残余应力引起的形面误差是综合误差的主部，其中残余应力等引起的非线性误差解析建模难度大。因此，在弹性误差模型的基础上，通过学习进化方法建立综合误差补偿模型的一种行之有效的途径。

1 加工误差补偿模型

文献[10]提出了一种具有自主学习进化能力的加工误差补偿模型及其学习进化机制，其中加工误差补偿模型如公式（7）所示。

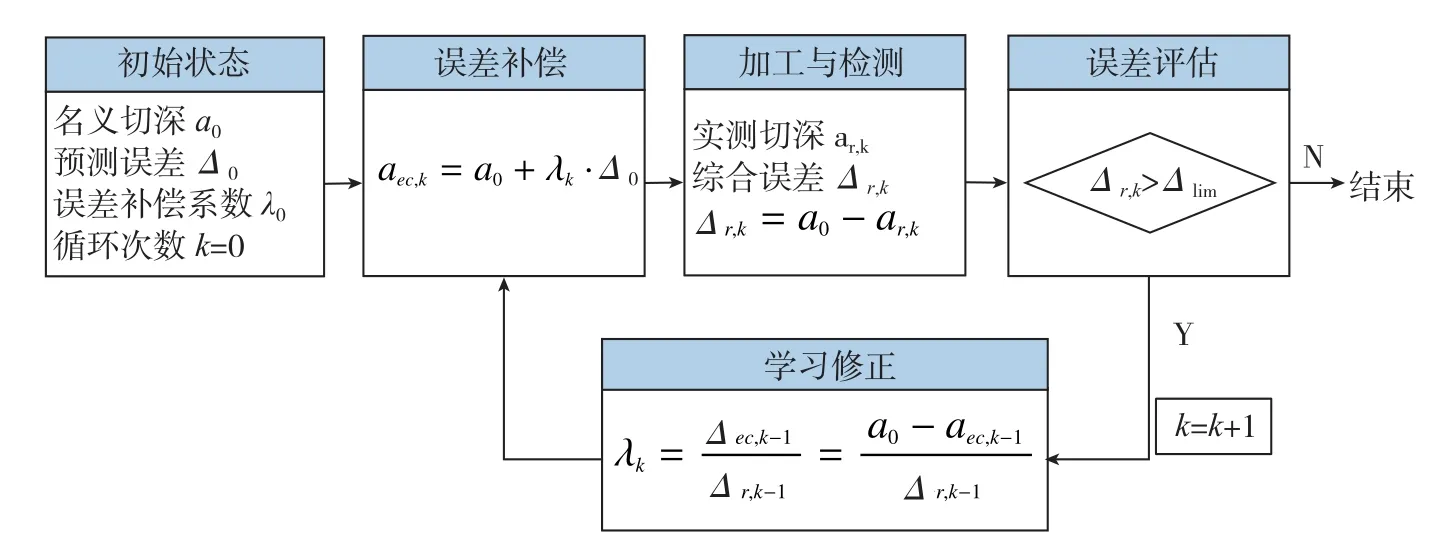
图9 误差补偿模型及其学习进化机制Fig.9 Processing error compensation model andevolution of iterative learning

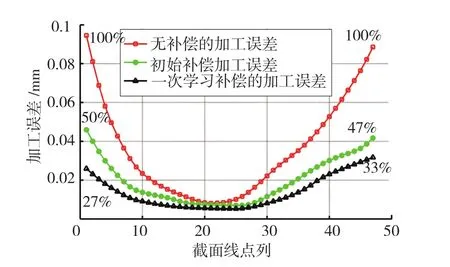
图10 误差补偿试验结果Fig.10 Experiment results of processing error compensation

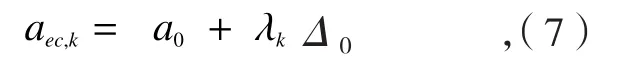
式中，aec,k是第k次误差补偿加工时切削深度的误差补偿值，a0为切削深度的名义值；Δ0为预测加工误差，λk为误差补偿系数。实际加工过程的误差补偿进化机制如图9所示。

图中的λ0为误差补偿系数的仿真预测值，Δlim为设计最大加工误差值， 是第k次加工后的综合误差。依据Δ0和λ0计算切削深度误差补偿值aec,k并进行初始误差补偿加工；加工后，测量实际切深ar,0并计算综合误差Δr,0；然后，进行误差评估，若满足加工要求，即Δr,k＜Δlim，则结束加工。反之，则修正误差补偿系数λk，重新计算切削深度的误差补偿值aec,k，再次进行补偿加工，直至满足加工要求。

2 加工误差补偿实例

在航空复杂薄壁零件的加工过程中，叶片的让刀变形最为突出，所以该误差补偿进化机制在叶片加工过程中进行了相关试验验证。首先采用理论切深对叶片进行切削加工；然后通过有限元仿真方法预测加工误差值 ，根据公式（7）计算实际切深进行补偿加工；最后采用图 9所示的迭代学习方法计算实际切深进行补偿加工。选择叶片中间某截面作为参照面，分别测量3次加工所得叶片的加工误差；试验测量结果如图10所示。

结果表明，通过弹性让刀误差仿真预测方法修正可以使误差降低到50%以下，说明弹性误差为整个误差的主要部分；经过一次学习可显著降低非线性误差，使综合误差降低到约30%。可见进化方法能显著地降低加工综合误差，能够有效地提高加工精度[11]。

误差补偿模型建立了零件完整加工过程的闭环控制。利用上述过程，在批量生产中，根据检测记录结果进行离线学习并积累知识。当出现超差时，触发决策控制与知识更新机制，实现故障处理与模型进化。

结束语

本文将航空复杂薄壁零件的加工过程在时域上进行多态划分，在三维空间里进行空间离散，建立了零件加工4维多态工序模型；采用变形映射技术建立了具体工步间零件几何演化模型；采用结构动力修改技术实现了零件动力学模型的演化与加工参数优选；建立刀具磨损演化模型，采用侦测加工技术实现了刀具磨损量的识别；最后通过零件加工误差补偿进化模型实现了零件加工过程的闭环控制，对于动态误差提出学习进化模型。智能加工技术对于提升航空复杂薄壁零件的生产效率、产品质量和可靠性具有重要作用。其关键技术是解决模型的精确化问题，以及如何提升模型的自适应能力和学习进化能力的问题。本文所提出的进化建模方法能够为航空零件的智能制造提供一种可行的建模途径。

[1]张定华，罗明，吴宝海，等. 智能加工技术的发展与应用[J]. 航空制造技术,2010(21):40-44.ZHANG Dinghua, LUO Ming, WU Baohai, et al. Development and application of intelligent machining technology[J]. Aeronautical Manufacturing Technology, 2010(21):40-44.

[2]郭恩明. 我国航空制造技术的现状及发展趋势[J]. 航空制造技术, 2002(1): 27-29.GUO Enming. Present status and development trends of aeronautical manufacturing technology in China[J]. Aeronautical Manufacturing Technology, 2002(1): 27-29.

[3]GUO H, FU X, CHEN F, et al. Asrigid-as-possible shape deformation and interpolation[J]. Journal of Visual Communication and Image Representation, 2008, 19(4): 245-255.

[4]韩飞燕，张定华，张莹，等. 基于虚拟控制面约束的机匣类零件工序模型建立方法[J]. 航空学报, 2015(10): 3465-3474.HAN Feiyan, ZHANG Dinghua, ZHANG Ying, et al. A method of generate intermediate process models for casing parts based on virtual control surface constraints[J]. Acta Aeronautica ET Astronautica Sinica, 2015(10): 3465-3474.

[5]ALAN S，BUDAK E，ÖZGÜVEN H N. Analytical prediction of part dynamics for machining stability analysis[J]. International Journal of Automation Technology, 2010, 4(3):259-267.

[6]ZHOU X, ZHANG D, LUO M, et al.Chatter stability prediction in four-axis milling of aero-engine casings with bull-nose end mill[J].Chinese Journal of Aeronautics, 2015, 28(6):1766-1773.

[7]周续，张定华，吴宝海，等. 材料切除对机匣铣削动力学与稳定性的影响[J]. 航空学报, 2016, 37(04):1352-1362.ZHOU Xu, ZHANG Dinghua, WU Baohai,et al. Dynamics and stability analysis in end milling of aero-engine casings considering material removal effect[J]. Acta Aeronautica ET Astronautica Sinica, 2016, 37(04):1352-1362.

[8]HOU Y, ZHANG D, WU B, et al.Milling force modeling of worn tool and tool flank wear recognition in end milling[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(3):1024-1035.

[9]HOU Y, ZHANG D, LUO M, et al. Tool flank wear recognition based on the variation of milling force vector in end milling[C]. IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besancon, 2014:1622-1627.

[10]杨建华，张定华，吴宝海. 考虑加工过程的复杂薄壁件加工综合误差补偿方法[J].航空学报, 2014(11): 3174-3181.YANG Jianhua, ZHANG Dinghua, WU Baohai. A comprehensive error compensation approach considering machining process for complex thin-wall parts machining[J]. Acta Aeronautica ET Astronautica Sinica,2014(11):3174-3181.

[11]YANG J, ZHANG D, LUO M, et al.A path planning method for error region grinding of aero-engine blades with free-form surface[J].Advanced Materials Research, 2014(875): 1127-1132.