通用型多语竞争与政策调控复杂Agent网络模型*

于群修，毕贵红，张寿明，曾振华.昆明理工大学 信息工程与自动化学院，昆明 6505002.昆明理工大学 电力工程学院，昆明 650500



通用型多语竞争与政策调控复杂Agent网络模型*

于群修1，毕贵红2+，张寿明1，曾振华1
1.昆明理工大学 信息工程与自动化学院，昆明 650500
2.昆明理工大学 电力工程学院，昆明 650500

Qunxiu,BI Guihong,ZHANG Shouming,et al.Universal complex agent network model for multi-lingual competition and policy intervention.Journal of Frontiers of Computer Science and Technology,2016,10(6): 822-837.

摘要：利用基于社会圈子理论的agent微观建模技术来构建语言竞争社会网络。构建的网络拓扑结构参数更接近实际社会网络参数，agent可以赋予空间属性，可以描述混合居住和分片聚居社会网络，而且具有动态特性。以三语竞争为例，提出了一种将网络中个体间的三语竞争分解为三个两种语言竞争的问题，给出了一种基于竞争原理的通用多语竞争复杂agent网络仿真建模方法。网络上的节点agent代表具有学习和遗忘功能的个体，每个个体均可以通过学习获得第二或第三种语言成为双语或三语者，也可以通过遗忘重新成为单语或双语者，同时agent考虑了语言的垂直传播。分析了语言地位、不同语言人口比例、移动人口比例、社会半径、不同语言人口的空间居住模式、语言传承率等因素及其综合调控措施对语言竞争的影响。仿真分析表明，该模型贴近实际社会，为多语竞争提供依据。

关键词：多语竞争；社会圈子；复杂网络；agent

ISSN 1673-9418CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(06)-0822-16

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

1　引言

据联合国统计，截止目前，有超过750种语言灭绝，现存6 000种语言，但超过50%的语言也处在危险之中，其中4%的语言使用者就占总人数的96%，25%的语言使用者不到1 000名，若不采取措施，在一个世纪之内这些语言（至少3 000种）都要灭亡。在中国，少数民族语言的多样性正在遭受严峻的考验。语言濒危的原因复杂多样，主要包括地理环境、人口分布与扩散、语言政策、语言地位和语言态度、语言环境和语言内部结构等因素及其相互作用，而且这些因素是随时空变化的，呈现异质性。为了拯救濒危语言，有必要对语言传播、竞争和调控的机理及动力学特性深入研究，以揭示语言衰退、消亡和共存的原因，进而寻求濒危语言保护和干预措施。

语言竞争传播演化现象是典型的不能假设、无法进行“真实性实验”的社会科学问题，而建立在社会仿真模型基础上的计算实验是可行的方案。社会仿真方法已经在文化版图空间演化和语言竞争等领域得到关注[1]。国际上语言竞争与演化动力学研究主要利用系统动力学方法、复杂系统建模和仿真方法。语言是一个复杂的适应性系统[2]，同时语言交流传播具有互动性，从而决定了人与人之间的接触网络是语言交流传播发生的基础。因此，语言交流传播系统是个复杂的社会网络系统，可以用复杂适应性系统理论及其建模方法、复杂网络及其建模方法以及两者结合的方法来研究语言竞争模型及其动力学性质。已有的研究方法包括：（1）利用微分方程来描述社会中两种语言竞争的动力学问题[3-6]；（2）基于agent的双语竞争建模方法[7-9]；（3）复杂agent网络的双语竞争建模方法[10-13]。复杂agent网络是目前最主要的语言竞争模型。

已有的研究方法综合考虑了语言的社会网络、人口密度、语言地位以及双语因素对语言共存的影响，在语言竞争动力学研究中取得了重要进展，但是目前还存在如下问题：（1）现有的复杂网络语言交流模型主要关注的是网络的拓扑结构特征，如小世界特征、无标度特性、高聚类特征和网络的社群结构等对语言交流传播的影响[14-15]，而对网络结构随时间的变化关注甚少，研究基本上都是以静态网络为基础的。而真实的社会接触网络由于受到人员在区域内或区域间流动的影响，使得网络拓扑结构特征发生变化，从而影响到其上的语言交流传播过程。（2）现实生活中多语言的竞争普遍存在，中国是一个多民族的国家，特别在云南等边疆地区三语及多语在一个地区进行交流很常见。因此，在两种语言竞争模型原理的基础上推广建立多语言的竞争模型来研究多语竞争与保护的动力学问题很有必要。

当前多语竞争研究主要集中在社会语言学方面[16]。有学者开始尝试将双语竞争的微分方程数学模型推广至三语及多语竞争问题[17]。但微分方程方法属于宏观建模方法，反映的是系统宏观变量之间的相互关系，不能描述语言竞争复杂社会系统中微观个体行为及其关系通过演化涌现出宏观语言态势的机制。已有的复杂agent网络建模方法的研究更多地用于双语竞争的情形。若将Castelló等人[15]的复杂agent网络模型直接推广到三语竞争情形，必然存在下列问题：（1）模型的通用性差；（2）模型的可解释性差；（3）模型的计算量巨大，耗时多。有必要进一步深入研究。

Hamill等人[18]提出了一种基于agent的社会圈子网络理论来构建具有多种实际社会网络统计特征的社会网络生成方法。它是一种基于微观个体行为生成社会网络的方法，网络的生成和演化由agent来管理，更加接近实际社会的运行机制，可以灵活描述大规模时空耦合社会网络。本文引入基于agent的社会圈子网络模型来研究个体行为和个体之间的语言传播构成的社会网络复杂agent网络模型。个体在语言竞争网络中通过个体间的交流获得某种语言能力或者失去某种语言能力。为了研究多语言竞争及其特有的动力学机制及保护措施，本文以三语竞争为例，提出了一种将网络中个体间三语竞争分解为3个两种语言的竞争问题，给出了一种基于双语竞争原理的通用多语竞争复杂agent网络仿真建模方法。网络上的节点agent代表具有学习和遗忘功能的个体，每个个体均可以通过学习获得第二或第三种语言成为双语或三语者，也可以通过遗忘重新成为单语或双语者。利用构建的通用型三语竞争复杂agent网络模型研究各种影响因素对语言传承与保护的影响。

2　基于agent的社会圈子理论的语言传播竞争模型

著名仿真学者Hamill等人[18]提出的基于agent的社会圈子网络理论可以构建具有多种实际社会网络统计特征的社会网络。该方法首先给每个agent赋予不同的社会交往半径和空间位置坐标，每个agent在自己的空间位置根据社会圈子原理生成社会关系网络，生成的网络具有大部分社会网络的特性：网络中个体的网络规模由于社会半径的不同而产生差异，规模随时间动态变化，网络中的社群人口密度较低，网络具有度正相关性，网络可以形成社群结构并具有平均路径短的特性。微观语言竞争传播网络属于一种典型的社会网络，社会圈子网络可以较完整地反映实际社会中语言竞争的特点，因此社会圈子网络可以用来研究微观语言竞争网络模型。

社会网络模型可以被看作一张社会地图，显示了人在网络中的分布与联结。网络中，人的社交范围用社会圈子表示，社会圈子的大小用社会半径表示，个体处于社会圈子范围内代表与该个体有关联，个体之间的距离与两者社会关系的密切程度成正比。在创建个体间联系时，要求双方都认识对方才认为两者是认识的，进而在两者之间产生连接，如图1（a）和图1（b）所示。本文设置3种社会半径，如图1 （c）所示，当个体agenti的社会圈子为圈子1时，有连接关系的个体个数为4个，随着社会半径的增加，社会圈子不断扩大，联系到的个体数目也在不断增加。现实社会中，人的交往范围不尽相同，如果个体的社交范围接近无限小，那么认识其他个体的可能性几乎为零；反之，个体之间全部有连接关系，即朋友的朋友也是朋友。少数人的社会交往范围比大多数人的范围大很多。

Fig.1　Generating principle of social relations图1　社会圈子中的社会关系生成原理

Fig.2　Influence of daily activity on individualnetworks and whole network图2　日常活动对个体网络以及整体网络的影响

社会圈子可以实现社会网络的动态特性，通过引入社会流动人口（短距离移动，即日常短途移动，长距离移动，即长途旅行等）来模拟现实社会中人口的日常活动，不同的日常活动会引起社会网络结构的变化。短距离移动代表个体在一个时间步长内移动一个单位长度的距离，因为移动的距离较小，所以人口的移动可能不会改变个体网络结构。图2（a）中agenti移动到A，那么agentj的个体网络结构改变；如果移动到B，因为仍在agenti的社交范围内，所以agentj的结构不变。长距离移动代表个体在一个时间步长内移动大于自身社会半径的距离，因为移动距离大于社会半径，所以个体网络以及整体网络结构都将改变。图2（b）中，agenti从A移动到B，因为移动距离L超过自身社会半径r，所以agenti网络结构以及整体网络结构一定改变。

现实社会中，人口的出生或死亡能够反映人口总数的动态变化，本文设置出生率Pb和死亡率Pd来反映这一特征。网络中，个体都以Pb的概率新生个体，以Pd的概率死亡。个体的新生或死亡能使网络人口动态变化，最终实现人口的动态平衡。死亡的个体断开所有的连接，新生的个体根据其所处的空间位置，在其社会半径内构建社会关系。基于社会圈子理论给agent赋予社会半径，同时也可以赋予agent空间坐标位置信息，agent根据坐标信息找到自己的空间位置，根据社会半径建立社会关系，因此可以建立不同空间分布的动态语言网络。如图3所示分别为3种语言人群混合居住和3种语言分片聚居网络。

Fig.3　Social network图3社会网络

3　双语竞争模型原理

Castelló等人[19]给出了基于两种语言的竞争模型，在一个有N个节点的网络中，节点表示掌握某种语言的个体，网络的边表示语言交流社会网络中个体的连接关系。在网络中，对于任意一个节点agenti有ki个邻居。每一个agenti有3种可能的语言状态：A，agent只掌握A语言；B，agent只掌握B语言；AB，agent使用双语，既可以讲A语言，也可以讲B语言。

公式中的参数Si(i=A,B)是语言的社会地位，它代表了一种语言的威望以及给讲这种语言的agenti带来的社会利益（比如对文化的发展，个人和职业的提升，国际性交流等）。这个参数的最大值为1，最小值为0，而且SA+SB=1。式（1）给出了一个agent从单语（A或B）变成双语AB的转换概率；式（2）给出了一个agent从双语变成单语的转换概率。从中可以发现，式（1）的转换概率Pi与要学习语言的社会地位和它的密度有关；式（2）的转换概率Pi与保留下来的语言的社会地位和被遗忘语言的密度有关。Castelló等人[19]重点描述了SA=SB=1/2时的情况。

需要注意的是，从单语A变为单语B或者从单语B变为单语A总是意味着要通过双语社区这个中间步骤来实现。

4　多语竞争模型原理

现实生活中多语言的竞争普遍存在，在两种语言竞争模型原理的基础上推广建立多语言的竞争模型来研究多语竞争与保护的动力学问题很必要。本文以三语为例，给出多语言竞争的通用模型。在三种语言竞争的模型中，考虑了一个有N个节点的网络中有3种竞争语言，分别是A、B、C。在网络上，对于任意一个邻居，每一个节点初始有3种可能的语言状态：A，只掌握A语言；B，只掌握B语言；C，只掌握C语言。通过网络中agent之间的学习，可能使单语者学会第二种语言成为三种双语者之一（即AB、BC和AC）；双语agent通过学习又可能获得第三种语言成为三语者（ABC）。网络中的双语或三语agent也可能遗忘其中一种语言又成为单语者（A、B或C）或双语者（AB、BC或AC）。通过学习和遗忘，网络中可能存在7种语言类型。从一种单语（如A）变为另一种单语（如C）中间要经过双语或者三语环节，不能直接从一种单语变为另一种单语。因此网络中存在着复杂的语言演化路径。

Fig.4　Language status evolutionary relationships of trilingual agent competition图4　三语竞争agent语言状态演化关系

4.1基于双语竞争原理的三语竞争模型

在语言竞争网络中通过交流获得某种语言能力或者因缺少交流机会失去某种语言能力。实际的语言交流环境中，每次交流可以看作网络中的个体选用A、B或C语言来进行两两交流实现语言学习和遗忘，逻辑上也可以把3种语言间的交流看成是3次两种语言的交流。因此在三语交流竞争过程中，把每一轮三语间的交流，通过每次忽略其中一种语言，用3次两种语言间的竞争来模拟一轮3种语言的竞争关系，即（1）A语言与B语言竞争，C语言不参与；（2）A语言与C语言竞争，B语言不参与；（3）B语言与C语言竞争，A语言不参与。

4.2语言学习及遗忘

（1）A、B两种语言间的学习和遗忘（忽略C语言）

Fig.5　Monolingual(A/B)learning/bilingual(AB) forgetting model图5　单语（A/B）学习/双语（AB）遗忘模型

Fig.6　Bilingual(AC/BC)learning/trilingual forgetting model图6　双语（AC/BC）学习/三语遗忘模型

（2）A、C两种语言间的学习和遗忘（忽略B语言）

Fig.7　Monolingual(A/C)learning/bilingual(AC) forgetting model图7　单语（A/C）学习/双语（AC）遗忘模型

由于忽略B语言，双语AB及双语BC也被视为单语A及单语C，根据式（1）的原理，双语AB、双语BC经过学习会转变为三语ABC，同时三语ABC（视为双语AC）按照遗忘公式又会转变为双语AB、双语BC。其转化过程如图8所示。

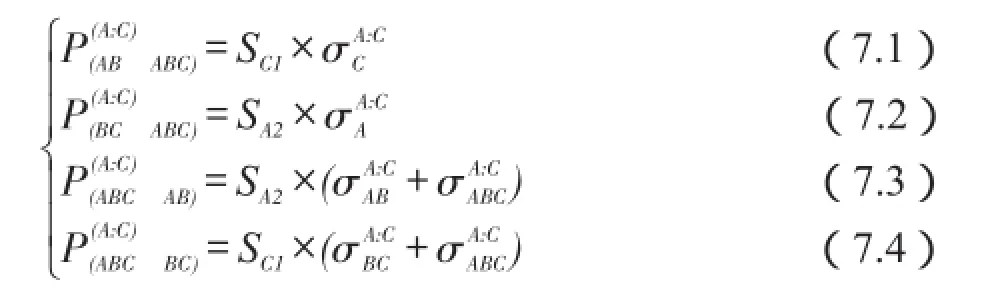
Fig.8　Bilingual(AB/BC)learning/trilingual forgetting model图8　双语（AB/BC）学习/三语遗忘模型

（3）B、C两种语言间的学习和遗忘（忽略A语言）

Fig.9　Monolingual(B/C)learning/bilingual(BC) forgetting model图9　单语（B/C）学习/双语（BC）遗忘模型

由于忽略A语言，双语AB及双语AC也被视为单语B及单语C，根据式（1）的原理，双语AB、双语AC经过学习会转变为三语ABC，同时三语ABC（视为双语BC）按照遗忘公式又会转变为双语AB、双语AC。其转化过程如图10所示。

Fig.10　Bilingual(AB/AC)learning/trilingual forgetting model图10　双语（AB/AC）学习/三语遗忘模型

4.3语言遗传

为了使模型更加符合现实，本文加入了出生率与死亡率。新出生的个体按一定概率继承父辈的语言。子代继承父辈语言时，并非是完全继承父辈的所有语言。受政治、经济、说话习惯、语言内部结构等影响，父辈到子代间可能发生语言的转用，并且这种语言的转用往往发生在两代之间[8]。

（1）双语遗传模型原理

每一个agent按照一定的概率死亡，死亡的agent按照一定的概率将自己的语言传递给后代。其中，双语AB将语言遗传给子代时，若满足概率 Py（0≤Py≤1），则子代完全继承父辈语言（子代为双语AB）；若满足概率1-Py，则子代语言为单语，且子代为单语A/B的概率均为1/2(1-Py)。同理双语AC及双语BC按照同样的概率将语言传递给子代。

（2）三语遗传模型原理

三语ABC将语言遗传给子代时，若满足概率Pt（0≤Pt≤1），则子代完全继承父辈语言（子代为三语ABC）；若满足概率1-Pt，则子代语言为双语或者三语，在概率1-Pt的基础上同时满足概率Py，则子代语言为双语且子代为双语AB/AC/BC的概率均为1/3Py。在概率1-Pt的基础上满足概率1-Py，则子代为单语，且子代为单语A/B/C的概率均为1/3 (1-Py)。

语言遗传概率模型如图11所示。

5　人工网络社会演化仿真流程

步骤1建立agent并初始化3种单语人口比例。创建N个agent并随机分布在200×200的二维空间网格内，分配3种单语者的人口比例(NA%,NB%,NC%)，3种人口比例之和为1，即NA%+NB%+NC%=1。

步骤2 agent属性设置。设置3组语言的社会地位，且满足SA1+SB1=1，SA2+SC1=1，SB2+SC2=1。设置小、中、大3种社会半径(RS,RM,RB)，并分配3种社会半径的人口比例(NofRS%、NofRM%、NofRB%)，3种人口比例之和1，即NofRS%+NofRM%+NofRB%=1。

步骤3设置人口流动比例及死亡率。在已经建立好的3种语言竞争网络模型中，设置一定比例的社会移动人口SocialShiftRate，并设置一定比例的死亡概率Pd、出生概率Pb。

步骤4生成社会网络。agent根据各自的社会半径，利用社会圈子原理建立社会网络（包括agent个体分片聚居与混合杂居，如图3所示）。

Fig.11　Language genetic probabilistic model图11　语言遗传概率模型

步骤5个体的语言交流。在建立好的网络模型中，个体通过学习和遗忘两种方式进行语言的交流。该部分的流程描述如下：

（1）A、B两种语言间的学习和遗忘

①忽略语言C（将双语AC/BC看作单语A/C，将三语ABC看作双语AB），单语A/B兼用单语B/A根据概率公式（4.1）、（4.2）成为双语AB；双语AC与双语BC竞争根据概率公式（5.1）、（5.2）成为三语ABC。

②忽略语言C，根据概率公式（4.3）、（4.4），双语AB成为单语A/B；根据概率公式（5.3）、（5.4），三语ABC成为双语AC/BC。

（2）A、C两种语言间的学习和遗忘

①忽略语言B（将双语AB/BC看作单语A/C，将三语ABC看作双语AC），单语A/C兼用单语C/A根据概率公式（6.1）、（6.2）成为双语AC；双语AB与双语BC竞争根据概率公式（7.1）、（7.2）成为三语ABC。

②忽略语言B，根据概率公式（6.3）、（6.4），双语AC成为单语A/C；根据概率公式（7.3）、（7.4），三语ABC成为双语AB/BC。

（3）B、C两种语言间的学习和遗忘

①忽略语言A（将双语AB/AC看作单语B/C，将三语ABC看作双语BC），单语B/C兼用单语C/B根据概率公式（8.1）、（8.2）成为双语BC；双语AB与双语AC竞争根据概率公式（9.1）、（9.2）成为三语ABC。

②忽略语言A，根据概率公式（8.3）、（8.4），双语BC成为单语B/C；根据概率公式（9.3）、（9.4），三语ABC成为双语AB/AC。

（4）遗传过程

①双语遗传：当父辈语言为双语将语言遗传给子代时，若满足概率Py，则子代为双语不变；若满足概率1-Py，则子代为单语，且子代为单语A/B/C的概率均为1/3(1-Py)。

②三语遗传：当父辈为三语将语言遗传给子代时，若满足概率Pt，则子代为三语ABC；若满足概率1-Pt的基础上同时满足概率Py，则子代为双语，且子代为双语AB/AC/BC的概率均为1/3Py；若满足概率1-Pt的基础上，同时满足概率1-Py，则子代为单语，且子代为单语A/B/C的概率均为1/3(1-Py)。

学习/遗忘/遗传三者同步进行。

步骤6网络动态更新。本文规定agent的出生率等于死亡率，网络中有agent死亡，死亡个体断开之前的连接，新生agent按照社会圈子原理生成新的连接。agent根据移动概率进行移动，当个体间连接的长度同时大于链两端的个体的社会半径时，连接断开，否则保持连接，断开之后的个体又会与其他个体按照社会圈子原理重新建立连接，形成新的社会网络。随着时间的更新，重复执行步骤5～6。

6　仿真结果分析

本文模型以NetLogo[20]为平台，主要分析了语言竞争的影响因素。多语社会，如有A、B、C语言的社会。通过语言兼用会出现单语（A、B、C）、双语（AB、AC、BC）及三语ABC，共7种话语人群，各种人群的人口比例与多种因素有着密切的关系。每个类型的实验在相同初始条件下重复20次，通过求均值得到最终实验结果。个体所处环境设定为200×200的网格空间。表1为具体参数。

6.1语言地位对三语传播的影响

图12表示降低语言地位差值后的对比图，图12 （a）初始状态 SA>SB>SC，3组语言地位分别为SA1=0.6，SB1=0.4；SA2=0.6，SC1=0.4；SB2=0.6，SC2=0.4。其中每组语言地位的和都为1。在此情景下，A的语言地位最高，B、C相对于A语言地位较低，但是B的语言地位高于C。图12（a）前200步计算机迭代中，由于语言之间的相互学习，出现了双语AB、AC和BC增加的趋势。因为单语A和单语B的人口最多，所以双语中AB的比例最大，同时双语通过学习获得第三语成为三语ABC，而且ABC的比例高于双语AB比例。从3个单语看，因为其中部分转换为双语和三语，所以3个单语都呈下降趋势，单语B和C下降最快，A下降最慢。总的来看，单语人数减少，双语和三语人数增加。200步之后，从图中可以看出，三语和双语人口在逐渐减少，而强势语言A的比例进一步增加，说明弱势语言兼用者正逐渐弃用母语，转用强势语言A；同时，弱势语言B、C进一步减少，并逐渐消亡，且最弱势语言C的消亡速度快于语言B，说明弱势语言通过兼用成为双语或三语，进一步又转用单语A。最后弱势语言B、C经过语言兼用、转用等阶段后，全部转变为强势语言A，单语B和C走向消亡。这也是大部分弱势语言已经或者正在经历的命运，为了改善弱势语言的生存状况，提高弱势语言的地位是最为有效的措施。

Table 1　Parameters and values of model表1　模型可调控参数和值

如图12（b）所示，模型中将单语A的语言地位降低，将单语B及单语C的语言地位提升，使弱势语言B、C的地位相对于A的地位差值降低。调整后的3组语言地位相对值分别为SA1=0.55，SB1=0.45；SA2=0.55，SC1=0.45；SB2=0.55，SC2=0.45。从图12 （b）可以看出，调整语言地位可以明显影响最终语言的走向，因为语言地位的提高，减少了语言兼用特别是转用的比例，所以弱势语言B、C的生存时间延长，双语和三语稳定存在的时间也明显延长。在实际社会生活中，提高弱势语言在社会、政治和文化方面的地位，提高经济发展水平，进而增强弱势语言者的自豪感和文化自觉，将会使得弱势语言地位得到提高，弱势语言的生存环境得到改善。

Fig.12　Influence of language status on language spread图12　语言地位对语言传播的影响

6.2语言人口比例对三语传播的影响

与图12（a）情景相比，其他参数不变，图13表示通过改变3种语言的人口比例来考查人口比例对语言传播趋势的影响。图13（a）模型初始的单语A、单语B和单语C人口比例分别为40%、35%和25%，属于强势语言和亚强势语言人口为主的居住格局。图13（b）模型三者的人口比例为25%、40%和35%，居住格局改变为以亚强势语言和弱势语言为主的社区。通过前后趋势曲线的对比可以很明显地看出，双语和三语的比例增加较快，存在的时间变长，亚强势语言及弱势语言持续的时间也更长。图13（a）仿真经过1 000次计算机迭代后所有语言基本完全转用为强势语言A（单语B、单语C、双语、三语的人口比例几乎降为零）。图13（b）中经过1 500次计算机迭代仍然有少量单语B、单语C及双语和三语的存在。但是通过对比图12的语言地位对语言传播的影响，发现改变语言人口比例对语言共存的最终走向并非起到决定性的影响。人口的增加就是小部分数据的平移，主要延长了语言兼用存在时间，当兼用者中部分逐渐转用强势语言A后，三者的比例关系发生改变，且其比例变化逐渐加快，最终通过语言转用全部转变为A语言，B、C语言消亡。

Fig.13　Influence of population proportion on language spread图13　人口比例对语言传播的影响

6.3移动人口对三语传播的影响

与图12（a）情景相比，其他参数不变，图14给出了增加社会移动人口比例后语言共存的关系。模型中移动人口比例由初始的8%增加到15%，结果显示在一定范围内增加移动人口的比例，人员流动性增加，加强了竞争语言之间的交流，双语（AB、AC、BC）和三语ABC这4种语言类型人数有较大增加，在双语和三语增加阶段，3种单语都呈快速减少趋势，特别是A语言减少的速度更快，表示增加人员流动，有利于强势语言兼用弱势语言。但是流动人口的增加对于语言共存时间的影响较小。弱势语言经过兼用语言高峰期后，有越来越多的双语和三语放弃母语转用强势语言，其速度甚至快于流动人口较少的情形。因此，随着现代社会流动性的增强，靠两种语言减少接触机会来保护弱势语言的目的是不可行的，在高流动性的社会中，要保护弱势语言就需要在弱势语言者学习优势语言的同时，热爱并传承自己的母语，减少语言转用，从而通过双语和三语的形式延长弱势语言保留时间。

Fig.14　Influence of mobile population on language spread图14　移动人口对语言传播的影响

6.4社会半径对三语传播的影响

与图12（a）情景相比，其他参数不变，图15表示了增大社会半径前后，语言共存状况的改变。随着社会进步和开放，人们的社会交往空间和人数都会增加，模型中3种社会圈子的社会半径由初始的小社会半径RS为10，中社会半径RM为12，大社会半径RB为14，变成RS为20，RM为22，RB为25。个体的圈子大小变化对语言传播竞争的影响较大，当个体圈子小时，网络密度也较小，随着个体圈子的扩大，网络中的连接不断增加，表示能联系到的个体范围增加，交流就会增加，语言消亡速度加快。

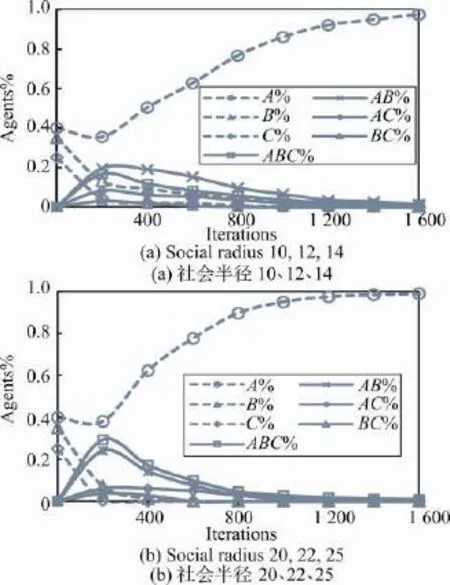
Fig.15　Influence of social radius on language spread图15　社会半径对语言传播的影响

图15（a）中亚强势语言（单语B）、弱势语言（单语C）、双语及三语者经过1 500步计算机迭代后，绝大部分转用强势语言A。而图15（b）中多语竞争的初期，单语转化为双语和三语的人数增加的速度明显快于图15（a）的情况，语言兼用人数比例增加，特别是最高峰时三语ABC的人数和双语AB的人数比例远高于图15（a），而且三语人数比例超过了双语AB的比例，有利于语言的兼用。但是，语言兼用高峰期过后，语言兼用人数比例逐渐减少，转用为强势语言A的人数增加较快，增加社会半径后弱势语言B、C、双语（AB、BC、AC）及三语ABC存在的时间缩短，在1 000步左右基本完全消亡。因此，适当控制社会圈子的规模，控制语言地位较低语言个体与语言地位较高语言个体之间的竞争交流，可以很好地维持两种语言共存的状态。如图所示，适当缩小社会半径后语言共存的情况，表明了地理上的隔绝有利于语言的保存。现实社会中，随着交通和通讯技术的发展，人们之间的时空隔绝越来越被淡化，人们的交往范围已经不受地理位置的限制。模型显示，从横向看，人口密度低，居住分散，交通闭塞的区域人们社会交往圈子小，网络密度低，语言衰减速度慢，语言容易保护。交通经济发达，人口居住集中的区域，人们社会交往圈子大，网络密度高，语言衰减速度快，语言保护和维持困难，是语言需要重点关注的区域。通过划分语言保护等级，区别制定保护政策，有利于区分轻重缓急。从纵向看，随着社会经济发展，人们交往的范围和网络密度呈增加趋势，如果不及时采取语言保护措施，语言消亡的趋势会增强。经济社会越发展，文化和语言保护越要加强。

6.5空间居住格局（分片聚居或混合杂居）对三语传播的影响

Fig.16　Influence of gathering live and scattered live on language spread图16　聚居与杂居对语言传播的影响

与图12（a）情景相比，其他参数不变，图16表示了不同语言的人口由混合居住变为各自聚居后语言共存状况的改变。模型中初始时刻让强势语言、亚强势语言及弱势语言的人口混合居住（即将所有人口随机分布到二维空间中），让各自语言的人口聚居（即将所有人口按语言的差别分块分布到二维空间中），所得的语言交流网络分别如图16（a）（b）所示。混合杂居加强了不同语言人口之间的交流，提升了人们学习除了母语之外的另外一种或两种语言的机会，打通了不同说话者之间的地域屏障，单语兼用速度较快，单语者存在的时间较短，语言兼用高峰期过后转用为强势语言A的人口比例快速增加，三语和双语存在的时间也较短，对语言的传播及保存有积极的影响。分片聚居给不同语言间增加了地理屏障，减少了不同语言的交流，兼用的双语比例增加缓慢，但是稳定很长时间后才逐渐减少。三语兼用人数的比例明显低于混合居住格局，因此弱势语言B、C存在的时间明显延长，强势语言A增加趋势缓慢。图16 （a）中，经过1 000次计算机迭代后所有语言基本已经完全转用强势语言A。而图16（b）中，各种语言在2 000次计算机迭代后仍有存在。由于分片聚居使得人们在各自的领域内仅掌握自己的母语而很少接触其他语言，不利于多语的产生，但是延长了单语和多语存在的时间。混合杂居在不改变语言地位的情况下，虽然短期内增加了语言兼用者的比例，但是提高了语言转用的比例，缩短了语言共存时间。不打破弱势语言聚居状况来发展弱势语言人群的社会经济水平，这在当前我国城镇化时期显得尤为重要。

6.6语言遗传率对三语传播的影响

与图12（a）情景相比，其他参数不变，图17表示增加遗传概率对语言共存的影响。模型中双语遗传率由初始的Py=0.3增加到0.7。同时，单语的遗传率为1-Py。三语遗传率由初始的Pt=0.3增加到0.7。结果显示增加双语及三语的遗传概率之后，双语及三语的存在时间延长。如图17（a）所示，模型经过1 200次计算机迭代之后双语基本已经消亡且很难出现三语人口，而图17（b）中在1 500步左右双语及三语仍有存在。三语在初始时刻到400步左右先增加后减小，并且图（b）三语增加的峰值明显高于图（a）。因此提高子代继承父代双语和三语的比例，增加父辈传授母语给子辈的机会，降低父辈和子辈直接转用强势语言进行交流的概率，增强母语继承的能力，需要全社会提高保护弱势语言的意识，特别是母语使用者的自我意识对传承母语至关重要。同时，学校增加双语教育措施，也是把母语传承给下一代的重要保证。

Fig.17　Influence of heritability on language spread图17　遗传率对语言传播的影响

6.7综合调控措施对多语传播的影响

通过对上述模型参数的分析，提升亚强势及弱势语言的语言地位可以提高该语言在经济、政治和文化方面的地位，增强持该种语言的自豪感，改变未来的趋势；增加相对弱势语言的人口比例有助于弱势语言的保存；移动人口的增加会增加弱势语言保护的难度，增加弱势语言消亡的可能性；社会半径的改变表明了地理上的隔绝有利于语言的保存；增加双语及三语的遗传概率，可以使更多的人成为双语或三语使用者。这些因素是相互影响相互制约的，需要充分考虑各种因素间的平衡调配。通过综合分析以及参数调整，并进行多次仿真，得到3种语言长期共存状态。图18表示通过对上述模型内各个参数的分析，并对参数进行适当调整后的模型仿真图。图中7类语言达到一种长期共存的状态。达到语言长期共存状态的模型参数设定值如下：（1）语言地位：SA1=0.55，SB1=0.45；SA2=0.55，SC1=0.45；SB2=0.55，SC2=0.45。（2）人口比例：NA%=45%，NB%=35%，NC%=30%；移动人口比例：SocialShiftRate=15%。（3）社会半径：NofRS%=10，NofRM%=12，NofRB%= 14。（4）双语及三语遗传率：Py=0.7，Pt=0.7。（5）总人口：N=2 000。（6）大、中、小3个半径人口比例：RS=45%，RM=30%，RB=25%。（7）人口出生率及死亡率：Pb=Pd=5%。

Fig.18　Comprehensive adjustment parameter图18 综合调整参数

7　结束语

本文基于社会圈子理论及双语竞争网络模型，以三语竞争为例，提出了多语竞争网络普适模型。并在此模型的基础上，分析了三语竞争中7种语言的形成过程及影响7类语言演化的因素。这些因素能正确描述动态语言传播网络的特点，并能从社会网络角度给出多语演化的定量解释，模型框架为进一步研究多语竞争提供了一个可行的新方法。仿真实验中通过调整语言地位、人口比例、移动人口数量、社会半径、不同语言人口之间的聚居与杂居、遗传率的大小分析对语言传播的影响，得到以下实验结果：

（1）提升语言地位SB或者SC可以提高该语言在经济、政治和文化方面的地位，增强持该种语言的自豪感，改变未来的趋势。

（2）增加弱势语言及亚强势语言的人口比例可以延长亚强势语言、弱势语言、双语和三语的消亡时间。

（3）移动人口的增加使人员流动性增加，双语及三语增加的同时3种单语呈快速减少趋势，人员流动性的增加对语言保护有消极影响；社会半径小，人们的交往范围小，地理上的封闭有利于语言的保存，增加社会半径，人们的交往范围加大，但增加了弱势语言濒危的速度。现代社会人们的流动性和交往范围日趋增大，语言保护面临的挑战增强。在规划少数民族地区社会经济发展时，需要把文化语言保护措施同时加以考虑，尽量做到本地城镇化，从而实现“离土不离乡”，大力发展区域民族文化，打造民族文化高地，为区域少数民族语言交流提供稳定的语言交流环境，形成民族语言保护岛屿，推动少数民族语言成为区域内重要的交流语言。

（4）分片聚居使说话者受限于地域屏障，加强了母语之间的交流机会，减弱了不同语言人口之间的交流，保证了人们学习母语的机会，对语言的传播及保存有积极的影响，而混合杂居则相反，表明地理上居住格局对语言保护有重要影响。语言濒危首先发生在城郊结合部混合居住的地区，而相对聚居地区语言保护紧迫性则相对较弱。

（5）提高子代继承父代双语和三语的比例，增加父辈传授母语给子辈的机会，降低父辈和子辈直接转用强势语言进行交流的概率，增强弱势语言共存的时间。这需要全社会提高保护弱势语言的意识，特别是母语使用者的自我意识对传承母语至关重要。同时，学校增加双语教育措施，也是把母语传承给下一代的重要保证。

（6）语言的保护需要多种措施协调配合，各种因素综合平衡后更容易达到语言共存状态。

仿真结果验证了社会学者定性研究结论，说明了模型的正确性。本文给出的复杂网络语言传播模型还有许多深入研究解决的问题，在空间网络中进行计算实验时，需要考虑实际的语言传播网络中不同空间分布中语言的人口比例、种类和语言地位的相对关系等因素，这些因素是随时间动态变化的，语言竞争复杂时空演化关系需要给予重视。地理信息系统（GIS）和复杂agent网络结合起来是可能的解决问题的方法，基于agent的社会圈子网络模型中，agent具有坐标位置、社会半径等空间信息，容易与GIS集成，本文的研究为此打下了一定的基础。

References:

[1]Yun Jian,Liu Xiangdong,Liu Yongkui.Computational modeling of a social phenomenon:evolution of cultural identity and cultural territory[J].Journal of Computer Research and Development,2013,50(12):2590-2602.

[2]Beckner C,Blythe R,Bybee J,et al.Language is a complex adaptive system:position paper[J].Language Learning,2009, 59(S1):1-26.

[3]Abrams D M,Strogatz S H.Modeling the dynamics of language death[J].Nature,2003,424:900.

[4]Mira J,Paredes A.Interlinguistic similarity and language death dynamics[J].Europhysics Letters,2005,69(6):1031-1034.

[5]Minett J W,Wang W S Y.Modeling endangered languages: the effects of bilingualism and social structure[J].Lingua, 2008,118(1):19-45.

[6]Zhang Menghan,Gong Tao.Principles of parametric estimation in modeling language competition[J].Proceedings of the National Academy of Sciences of the United States ofAmerica,2013,110(24):9698-9703.

[7]Kandler A,Steele J.Ecological models of language competition[J].Journal of Biological Theory,2008,3(2):164-173.

[8]Beltran F S,Herrando S,Ferreres D,et al.Forecasting a language shift based on cellular automata[J].Journal of Artificial Societies and Social Simulation,2009,12(3):5.

[9]An Zhecheng,Pan Qiuhui,Yu Guangying,et al.The spatial distribution of clusters and the formation of mixed languages in bilingual competition[J].Physica A:Statistical Mechanics and itsApplications,2012,391(20):4943-4952.

[10]Stauffer D,Castelló X,Eguíluz V M,et al.Microscopic Abrams-Strogatz model of language competition[J].Physica A:Statistical Mechanics and its Applications,2007,374(2): 835-842.

[11]Castelló X,Eguíluz V M,Miguel M S.Ordering dynamics with two non-excluding options:bilingualism in language competition[J].New Journal of Physics,2006,8(12):308-322.

[12]Castelló X,Loureiro-Porto L,Miguel M S.Agent-based models of language competition[J].International Journal of the Sociology of Language,2013(221):21-51.

[13]Wang Chao,Bi Guihong,Zhang Shouming,et al.Agentbased language competition model with social circles network[J].Journal of Computer Application,2014,34(8): 2202-2208.

[14]Castelló X,Toivonen R,Eguiluz V M,et al.Anomalous lifetime distributions and topological traps in ordering dynamics[J]. Europhysics Letters,2007,79(9):66006.

[15]Toivonen R,CastellóX,Eguiluz V M,et al.Broad lifetime distributions for ordering dynamics in complex networks[J]. Physical Review E,2009,79(1):016109.

[16]Lei Lei.Third or additional language acquisition[J].Modern Foreign Language,2010,33(3):213-214.

[17]Fujie R,Aihara K,Masuda N.A model of competition amongmore than two languages[J].Journal of Statistical Physics,2012,151(1):289-303.

[18]Hamill L,Gilbert N.Social circles:a simple structure for agent-based social network models[J].Journal of Artificial Societies and Social Simulation,2009,12(23):3.

[19]Castelló X,Loureiro-Porto L,Eguíluz V M,et al.Thefate of bilingualism in a model of languagecompetition[C]//Advancing Social Simulation:The First World Congress.Tokyo: Springer Japan,2007:83-94.

[20]Wilensky U.NetLogo[EB/OL].Center for Connected Learning and Computer-Based Modeling,Northwestern University, Evanston,USA(2012)[2015-04-28].http://ccl.northwestern. edu/netlogo/.

附中文参考文献:

[1]云健,刘向东,刘勇奎.文化认同及文化版图演化现象的社会计算模型[J].计算机研究与发展,2013,50(12):2590-2602.

[13]王超,毕贵红,张寿明,等.基于Agent社会圈子网络的语言竞争模型[J].计算机应用,2014,34(8):2202-2208.

[16]雷蕾.《三语或多语习得》述评[J].现代外语,2010,33(3): 213-214.

YU Qunxiu was born in 1986.He is an M.S.candidate at Kunming University of Science and Technology.His research interests include embedded system,the modeling and simulation of complex system and complex network,etc.

于群修（1986—），男，山东青岛人，昆明理工大学硕士研究生，主要研究领域为嵌入式系统，复杂系统与复杂网络建模与仿真等。

BI Guihong was born in 1968.He received the Ph.D.degree in production process logistics from Kunming University of Science and Technology in 2008.Now he is a professor and M.S.supervisor at Kunming University of Science and Technology.His research interests include social and economic system simulation,etc.

毕贵红（1968—），男，云南石林人，2008年于昆明理工大学获得博士学位，现为昆明理工大学教授、硕士生导师，主要研究领域为社会和经济系统仿真等。

ZHANG Shouming was born in 1966.He is a professor and M.S.supervisor at Kunming University of Science and Technology.His research interests include the multi-dimensional information fusion and modeling of complex systems,etc.

张寿明（1966—），男，云南大理人，昆明理工大学教授、硕士生导师，主要研究领域为复杂系统的多维信息融合与建模等。

ZENG Zhenhua was born in 1987.He is an M.S.candidate at Kunming University of Science and Technology.His research interests include the modeling and simulation of complex systems and complex networks,etc.

曾振华（1987—），男，湖南衡阳人，昆明理工大学硕士研究生，主要研究领域为复杂系统与复杂网络建模与仿真等。

*The National Natural Science Foundation of China under Grand No.61364022(国家自然科学基金). Received 2015-06,Accepted 2015-08.

CNKI网络优先出版:2015-08-13,http://www.cnki.net/kcms/detail/11.5602.TP.20150813.1635.005.html

+Corresponding author:E-mail:km_bgh@163.comYU

文献标志码：A

中图分类号：TP391.9

doi:10.3778/j.issn.1673-9418.1506056

Universal Complex Agent Network Model for Multi-Lingual Competition and Policy Interventionƽ

YU Qunxiu1,BI Guihong2+,ZHANG Shouming1,ZENG Zhenhua1
1.College of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China
2.College of Electric Power Engineering,Kunming University of Science and Technology,Kunming 650500,China

Abstract:This paper proposes a dynamic social network model for the competition among three languages with agent based modeling method and social circles theory.The parameters of the topological structure of constructed social network are more close to the parameters of actual social network.The individual agents in the network can give space attribute and can describe mixed habitation in a region with different languages and separation habitation in individual area with a language,so the constructed social network is endowed with dynamic characteristics.Taking the competition among three languages as an example,this paper proposes a method that the competition among three languages is decomposed into three times of bilingual competition,and presents a universal complex agent network model for multi-lingual competition and policy intervention.The agents on the network represent the individual which has the function of learning and forgetting.And each agent can gain a second or third language to becomebilingual or trilingual by learning and can forget to become monolingual or bilingual.The vertical transmission of language is taken into account.The simulating analysis of the proposed model shows that the system parameters of language status,the proportion of people of different languages,the proportion of mobile population,social radius, living space model and integrated control measures can affect the results of simulation.The simulation results show that the model is close to the actual society and provides the basis for multi-lingual competition.

Key words:multi-lingual competition;social circle network;complex network;agent