异构三维片上网络布局优化的超图划分算法*

宋国治，张大坤，马杰超，涂　遥，刘　畅天津工业大学 计算机科学与软件学院，天津 300387



异构三维片上网络布局优化的超图划分算法*

宋国治+，张大坤，马杰超，涂遥，刘畅
天津工业大学 计算机科学与软件学院，天津 300387

SONG Guozhi,ZHANG Dakun,MA Jiechao,et al.Hyper-graph partition algorithms for heterogeneous 3D network-on-chip floorplanning optimization.Journal of Frontiers of Computer Science and Technology, 2016,10(6):811-821.

摘要：片上网络作为一种将大量嵌入式内核集成到单个晶圆片上的可行性技术，与传统片上系统相比，更能应对未来需要更大规模集成内核的挑战，从而得到了更广泛的应用。然而，目前大多数对片上网络的研究是在规则的架构上进行的，即假定所有单元片面积相同，但是这种假设过于理想化。因此，基于异构布局的三维片上网络的研究是非常有必要的，而其中网络单元的合理划分对片上网络的性能有着重要的影响。介绍了基于异构布局的三维片上网络架构，并将超大规模集成网络中的单元映射成一张超图，并且对此超图进行了多级划分。在算法框架的不同阶段，介绍了常见的算法，并且对相应算法的潜在问题进行分析，随后对这几种算法进行改进以提高片上网络的性能。最后，通过对几个常见的超大规模集成单元数据集进行实验分析，比较了不同阶段的算法对该片上网络各个性能的影响，并得出各个数据集上最优的hMetis算法框架。

关键词：三维片上网络；异构布局；超图划分；hMetis

ISSN 1673-9418CODEN JKYTA8

Journal of Frontiers of Computer Science andTechnology

1673-9418/2016/10(06)-0811-11

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

1　引言

随着芯片制造业的迅速发展，芯片规模日益扩大，原有的总线结构和点到点的互连已经不能满足通信的需求。因此，片上网络应运而生。

由于片上网络本身的规模十分庞大，并且受到现有计算机计算能力的限制，需要将网络上原有的单元进行重新划分布局，来提高该片上网络的性能。超图具有的一些特征可以用来表示一些非规则问题中的结构，例如分布式数据库中的数据相关性，超大规模集成电路（very large scale integration，VLSI）中元件的连通性[1]等。超图能够很好地反映超大规模集成元件的划分布局。

对于三维片上网络，之前的许多研究都假设所有单元片的面积都是相同的，即同构结构，但是不同的公司所生产的不同型号的IP（intellectual property）单元片面积各不相同，因此这种假设是很不实际的。针对这一类单元片面积不同的片上网络，美国北达科他州立大学的de Paulo和Ababei提出了一种基于异构布局的二层片上网络架构[2]和三层片上网络架构[3]，分别如图1（b）和图（c）所示。此架构的特点在于将单元片和路由器进行分离处理，在基于异构布局的二层片上网络架构中，Layer 2为均匀规则分布的Mesh架构的路由器，而在Layer 1上是面积不规则的单元片。在基于异构的三层片上网络架构中，Layer 2为规则的路由器，Layer 1和Layer 3为异构的单元片。然而，对于如何将原片上网络单元片划分到Layer 1和Layer 3，有着众多的划分方式。不同的划分方法对片上网络最终性能有着很大的影响。对于该步骤的划分问题可以被抽象为是对超图进行的二分问题。图1为基于异构布局的三维片上网络，其中（a）为初始不带路由器的布图；（b）为二层架构；（c）为三层架构；（d）为每个IP核面积扩展以容纳网络接口、路由器及物理连接布线后的二维实现。

Fig.1　3D NoC with heterogeneous floorplan图1　基于异构布局的三维片上网络

在过去的几十年间，已经有许多国内外该领域的相关学者对图的划分问题开展了广泛深入的研究，特别是超图划分算法的研究已引起越来越多业界人士的关注。早在20世纪70年代美国的普林斯顿大学的Kernighan和Lin就提出了组迁移（group migration）算法的思想[4]，并设计了经典的KL算法。该算法的主要思想是将一个网络节点图分割成两个相等的节点集合，使得连接两个集合的边权最小。KL算法是基于无向二分图划分的第一个有效的启发式算法。

之后Fiduccia和Mattheyses[5]提出了著名的FM算法，在该算法中，主要引入了单元增益值和面积约束函数。该算法也是首先产生一个初始划分，然后进行顶点的迁移，并且每次迁移以单元的形式从一个子集迁移到另一个子集当中，而且元件的移动要考虑是否满足约束函数，是否降低了域的解空间。

最近，Karypis和Kumar提出了一种基于图的多级划分算法[6-7]，随后他们又将该理论应用到超图的多级划分中[8]，基于超图的多级划分算法可以得到一个较好的二分超图。

本文将片上网络中的单元映射成超图，介绍了基于超图划分的多级划分算法框架，对这些常用的划分算法进行了分析改进，并且将其运用到片上网络的设计中，以提高片上网络的性能。在得到一个划分完的二分超图后，将两个子图分别进行合理的分配，以求得到较好的网络性能。在实验中采用了模拟退火算法来对该子图进行合理的布局。而片上网络的吞吐量和网络的运行时间被用作衡量整个算法框架的标准。

2　超图多级划分的基本框架

2.1超图的基本概念

所谓超图（hyper-graph），是对图的一种扩展。在超图中，一条边连接着任意多个点，每条超边是超图点集的一个非空子集。超图H可以定义为一对边和顶点的集合H=(X,E)[9]，其中X为顶点的集合，E为X的非空子集。

本文将具体的电路映射成为超图，具体映射方法可参照图2[10]。图2（a）表示片上网络中的电路逻辑图，每个元件都是从左端输入，从右端输出。对于每一个元件，以该元件的输出端为输入信号的所有元件可以组成一条超边。以图2（b）中的B元件为例，以B元件的输出端为输入信号的有D、E、F，因此可以将B与D、E、F组成一个超边，而其中这4个元件被映射为超边中的4个顶点。于是图2（a）中的各个元件可以被映射成为一张超图，如图2（b）所示。

下面给出在超图模型中所涉及的两个定义：

定义1（顶点权重）对于超图H=(X，E)的权值，顶点集V的权值之和称为超图的权值。其中超边集E的权重即为该超边中的顶点的权值之和。在电路划分问题中，一般将单元片的面积作为超图中顶点的权值。

定义2（超边切）对于超边e，如果其所包含的顶点存在于其他不同的超边之中，称该超边为其他超边的超边切[11]。

在将超图进行切割时，每一条超边看作一个子图，其中子图中每两个定点都是相互连接的，连接的权值为超边的权重比上超边的势（cardinality）。所谓势，是指该超边所包含的顶点的个数。该子图被切割为H1和H2。超图的超边切可定义为：

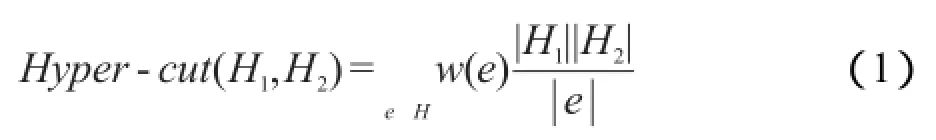
其中，w(e)为该超边的权重；||H1、||H2为被切割后两个子图的势； ||e为切割前原超边的势。

Fig.2　Mapping of devices on 3D network-on-chip图2　三维片上网络中元件的映射

由于超边切的数量和超边的大小成正比关系[12]，想要得到一种较好的划分，应研究如何能够更好地降低超边的大小。

2.2hMetis算法框架

多级划分的算法框架首先在图划分问题中由明尼苏达大学的Karypis等人[7,10,13]提出，并且将此框架推广到了超图划分的问题中。此框架使用不同的算法将超图的边和顶点进行合并，从而得到一个有原超图特征的较小的超图。

hMetis划分算法框架可分为3个阶段，粗化阶段，初始划分阶段，迁移优化阶段，如图3所示[9]。在粗化阶段，将某些超图的节点结合在一起，得到下一级粗化超图，重复此过程直到粗化超图足够小为止，即得到一个最小的超图。在初始划分阶段，对该最小超图进行对分，得到一个初始划分。因为许多超图划分算法在超图比较大的情况下得不到较好的划分性能，所以在最后的迁移优化阶段，将划分从最小的超图投影回原始的超图，在每一水平层的粗化超图中，对划分进行迁移优化。

Fig.3　Various phases of multilevel graph bisection图3　hMetis框架算法的不同阶段

本文2.2.1小节介绍粗化阶段所使用的粗化算法，2.2.2小节介绍初始划分阶段的具体实现，2.2.3小节介绍迁移优化的相关算法。

2.2.1粗化阶段算法

在粗化阶段，超图中的一系列顶点被合并成一个顶点，生成一系列的逐渐变小的超图，而这些粗化后的超图的性能不会明显比原图差。因为将原超图进行多级划分的目的是为了能在迁移优化阶段得到一种更好的超图划分。基于KL-FM等系列的启发式算法能在较小的超图中发挥较好的性能，但是随着超图的顶点数和边数的增大，这些启发式优化算法将不再适用。

本文将介绍3种常见的粗化阶段顶点不同的合并算法。（1）边粗化（edge coarsening，EC）选择在同一超边内的两个顶点，将它们合并成一个顶点。（2）超边粗化（hyperedge coarsening，HEC）将属于同一个超边中所有独立的顶点合并成一个顶点。（3）改进超边粗化（modified hyperedge coarsening，MHEC）是基于第二种方法的优化，因为一旦将超图中的所有顶点合并后，和该超边相关但是没有被合并的顶点与合并后的顶点在权值上会有很大的差异，这将会降低超图的划分效率。为了在优化阶段得到更好的划分，可以将超图中未被合并的那一部分顶点进行合并。该3种算法的具体合并方式如下。

（1）边粗化

在边粗化方案中，各个顶点被随机地访问，对于任意一个顶点v，所有和v属于同一个超边并且尚未被其他顶点匹配的顶点将在v的匹配序列之内，在此序列中，可以将计算出的能与v匹配合并后得到最大权值的顶点进行匹配合并，而合并后所得到的权值为两个顶点的权值之和。合并后超边的权值为：

其中，e为超边所表示的势的大小。

在边粗化算法中，是将超图中的超边间接地看作一般图中的边，然而这里并没有真正地将超边转化为一般的边，因此被粗化后的超图仍能较好地保有原超图的特征。

（2）超边粗化

尽管边粗化方案能够逐渐地生成可以很好地拥有原超图特征的许多更小的超图，但是该方案每次粗化只能合并两个匹配的顶点，该过程需要粗化许多次才能得到一个较小的超图。因此，该方案并不能很快地得到足够小的超图。

在超边粗化方案中是将属于同一个超边中的所有顶点合并为一个顶点。具体的实现方式如下：该方案将超边以权重的非递增顺序排列并依次访问，当遇到超边的权重相同时，以超边大小的非递减顺序访问。按照此访问顺序，对于每一个超边中还未被匹配的所有顶点，将此顶点集进行合并。因此，该方案优先选择那些具有较大权值和较小大小的超边。最后，直到所有的超边完全被访问，然后可以将这些被匹配完并且合并后的顶点作为下一级将被粗化的超图。而那些未被合并的顶点将会简单地被复制到下一级被粗化的超图。

（3）改进超边粗化

超边粗化算法能够显著地减小超边的权重，然而在每个粗化阶段，大多数超边并没有被合并，因为属于它们的顶点已经由其他的超边进行了合并。这导致了两个问题：第一，超边的大小减小得并不充分，使得基于FM-KL系列算法的迁移优化阶段变得困难。第二，顶点的权重（即已被合并的顶点的权重）被粗化的程度显著不同，导致超图形状的扭曲。

为了解决这一问题，可以在进行完HEC方案后，重新按照序列中的访问次序访问超边，并且对那些没有被合并的顶点进行合并。

2.2.2初始划分阶段算法

经过粗化阶段以后，会得到一个足够小的超图，通常来说顶点数|V|<100为一个比较合适的标准值。而在初始划分阶段，通常进行二分法，即使用一条线将超图分割为两个部分。在初始划分中考虑负载的平衡和顶点之间的通信。

在后面实验部分所使用的是一种较为简单并且效果比较好的划分算法。其主要思想是任意选取一个顶点，并由该顶点开始，依据图的连通性，逐渐地生长，直到生长出来半数原图的顶点。

具体的算法描述如下：

步骤1任意选取超图的一个顶点，记为0。

步骤2按照广度优先遍历方式，从顶点0开始遍历图，与顶点0相邻的顶点均记为1；循环此过程，与顶点i相邻的顶点均记为i+1。

步骤3当所有访问过的顶点数目等于顶点总数的一半的时候，算法结束。

然而，该算法所得出的二分图并不是最优解，下面将从两个角度出发，考虑对其进行优化。

第一，初始顶点的选取角度。容易得出，当所选的顶点位于图的边缘部分，将能得到一个较好的二分图。与之相反，如果所选取的顶点位于图的中间部分，那么该图并不能被很好地平衡划分。因此可以对该算法进行限制。假定初始所选取的顶点在一个特定的区域之中（图的边界范围），然后随机选取该范围内的顶点作为初始顶点。

第二，在初始划分阶段所得到的拥有最小超边切的划分方式，在经过迁移优化阶段投射为原超图后，也许并不是原超图所拥有的最小超边切方式。也许在该阶段拥有非最小超边切数量的划分算法在经过迁移优化后得到原超图的最优划分。因此，这里不仅只选择在此阶段的一个最优的划分方式，而是选择多个在此阶段划分结果较好的几种方式。但是，同时计算多种方式会大大增加该框架的运行时间。

在实验开始时先随机生成10种不同的初始划分，并且淘汰掉那些超边切数量多于最小超边切数量10%的初始划分。这样就过滤掉那些确实比较差的划分方式，并且减少在迁移优化阶段的运行总时间。

2.2.3迁移优化阶段算法

（1）KL算法

Kernighan和Lin提出了组迁移算法[4]思想，并设计了KL算法。该算法是将一个网络节点图分割成两个相等的节点集合，使得连接两个集合的边权最小。该算法是基于无向二分图划分的第一个有效的启发式算法，以后的图划分算法大多数是对KL算法进行的改进。

KL算法从一个等分的初始划分入手，通过两个划分中的结点互换减少边割线的数目，比较迁移前后的增益，循环此步骤，直到没有任何改进为止。在迁移过程中的增益（gain）可以被定义为：

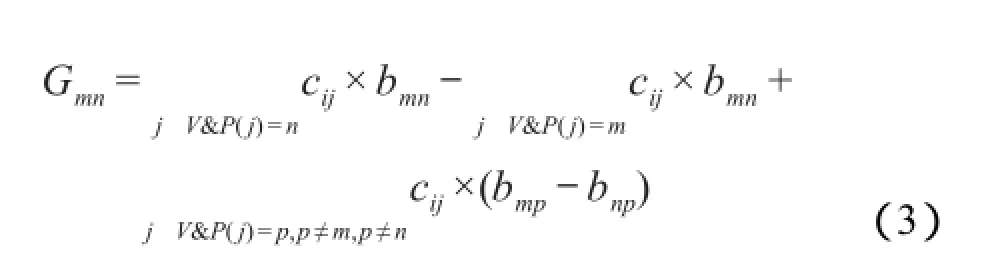
其中函数P(j)返回一个顶点j的当前部分。

（2）FM算法

Fiduccia和Mattheyses[14]提出了著名的FM算法，该算法是对KL算法的一次较大的改进。在该算法中，主要引入了单元的增益值和面积的约束函数。该算法也是首先产生一个初始划分，然后进行顶点迁移，并且每次迁移以单元的形式从一个子集迁移到另一个子集当中，而且元件的移动要考虑是否满足约束函数，是否降低了域的解空间。虽然FM算法速度很快（为线性时间复杂度），但是FM算法很容易陷入局部最优[15]。

FM算法的主要思想是每次将割线一侧的顶点迁移到割线的另一侧。交换的标准为：

①该顶点交换以后，图的负载平衡性改进为最大，即使此改进是负的。

②如果顶点交换以后图的负载改进不变，则选择交换以后能够使图的割边权最小的顶点。

将负载平衡作为第一标准是因为FM算法不像KL算法那样，每次交换一个顶点对却不会有交换后负载差异变大的情况。

因此，FM算法的时间复杂度为O(P)，其中P为电路线网端点（PIN）的数目。对于大多数图来说，这是一个相当不错的改进。因为只有完全图的边数才能达到O(|V2|)，其中||V 为顶点数，所以O(P)<< O(|V|2)。但是实际上，每次交换完毕一个顶点以后，更新顶点增益权值，仍然需要O(|V|)，因此实际上FM算法仍然有相当大的改进空间。

（3）EEFM算法

EEFM算法（early-exit FM）是基于FM的一种算法，该算法是在每次进行FM算法循环之前先判断该划分是否能相对地提高增益值。如果是在超图顶点较小的情况下，并且该划分并不能很好地提高增益，FM算法便直接退出循环。

3　hMetis框架算法的分析与改进

3.1粗化阶段算法分析与改进

研究发现，在上文所述的3种粗化算法中有一些算法存在一些潜在的问题，本文将针对上述算法进行潜在问题分析，并对其做出适当的改进。

在EC算法中，无论是图的粗化还是超图的粗化，都会导致一个潜在的问题。这个问题就是EC方案着力于寻找一个最小超边切的粗化方式，而并不是去寻找一种最好的粗化方式。当超图中原来就存在一种较好的图的划分，但是如果是基于EC算法，直接寻找最大权值的顶点并且合并，将会破坏原来较好的划分，从而增加了迁移优化阶段的难度。在原图中存在一个较好的划分，而两个子图只被一个超边所连接。如果基于EC算法，会发现原超图的一个较好的划分被破坏。这将导致在随后的迁移优化阶段已合并后的EF顶点不论如何迁移，都不能减少超边切数量。

类似的情况在HEC算法中也存在，因此需要寻找一种较好的方法来提高粗化阶段的性能。

（1）First Choice（FC）

FC粗化算法基于上文所述的EC算法，与之不同的是FC算法降低了EC算法中的要求。在EC算法中，顶点只能与未被匹配的其他顶点进行匹配，而这会导致上述对较好原图划分的破坏。因此，在FC算法中，对于任意的顶点v，所有的顶点（被匹配的和未被匹配的顶点）将会被加入到v的待匹配序列，在此序列中可以寻找一个权值最大的顶点来和v进行匹配并合并。如果该顶点原先已经被匹配，本文会计算两种不同匹配方案的增益，并且选取更有利于迁移优化的方案进行合并。该算法的伪代码如图4所示。

（2）Hybrid-First Choice（HFC）

该算法是基于FC算法的一种改进算法，由于FC算法是为了防止EC算法中打破原超图中天然的划分，而EC算法是一种基于贪心的算法，从而FC算法防止了顶点的贪心合并，在超边切的数量上会有所增加。

因此，本文将贪心算法和对EC算法改进后的FC算法进行组合，从而得到HFC算法。在此算法中，顶点的合并沿着最快地减小超边数量的方向进行。

Fig.4　FC algorithm图4FC算法

3.2迁移优化阶段算法分析与改进（1-way FM）

从上文FM算法的分析可以得出，算法在每次交换完毕一个顶点以后，都需要更新一次顶点的增益权值，因此该算法的复杂度仍然需要O(|V|)，从而FM算法仍然有相当大的改进空间。

前面提到的KL和FM算法能在迁移优化阶段得到很好的二分优化，但是这仅仅是二分子图中的最优的划分方案。而往往局部的最优并不代表是原超图的最优划分，于是尽量避免使迁移优化过程陷入局部最优就成为关键问题。

在1-way FM算法中，规定在每一次循环中，顶点的迁移只能沿同一个方向进行。显然，这样的策略能够有效地跳出局部最优。

4　实验结果与分析

4.1测试用例

本文实验中所使用的6个测试用例，以及它们的属性值如表1所示。该测试用例采用的是传统的MCNC用例，面积被扩展来获得一个大约1 cm×1 cm的平均尺寸，采用与参考文献[3]相同的参数配置，以此为基准计算通信量和模块间的初始连接与用例布局。

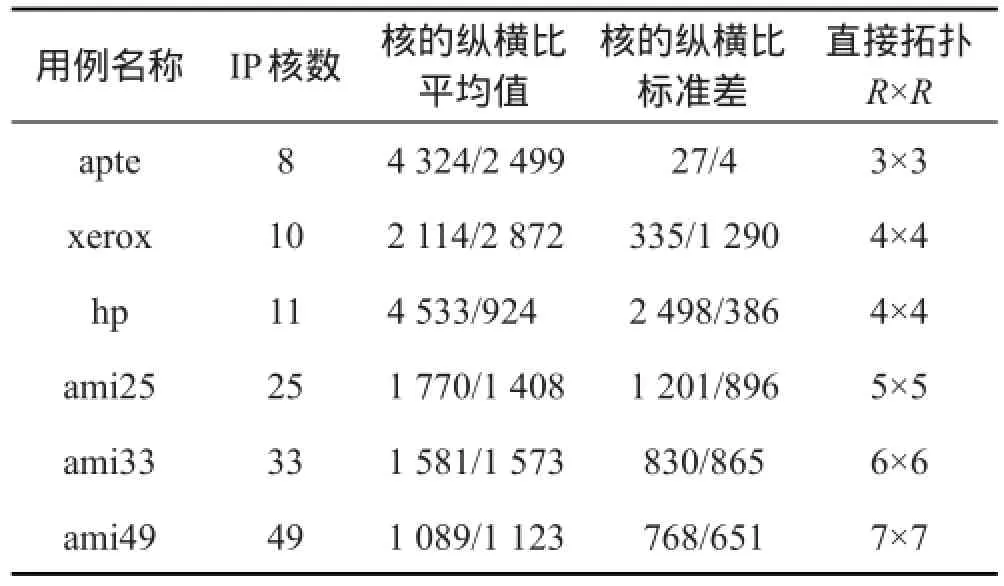
Table 1　Property values used in test cases表1　使用的测试用例的属性值

本文将使用三维片上网络的吞吐量和该片上网络所运行的时间来衡量该片上网络的性能。吞吐量的计算主要关注的是每个结点到其他结点获得的网络吞吐量的值，以及整个网络的平均吞吐量。

4.2粗化阶段算法对性能的影响

本文将粗化阶段的算法EC和HEC与改进后的算法FC和HEC进行比较，所比较的性能标准为该三维片上网络的运行时间和网络吞吐量。

由图5可见，对于不同的测试用例，该算法所运行的时间差别非常大。其中ami49在不同的粗化算法下差别较大，而xerox随着粗化算法的不同变化幅度较小。

Fig.5　Comparison of runtime with different coarsening algorithms for 3D NoCs图5　不同粗化算法在片上网络的运行时间

原始的HEC算法所使用的时间在大多数情况下（除了xerox）比原始的EC算法所使用的时间多。而经过改进的FC算法在IP单元片数较大或者较小的时候能够得到一个较好的划分。而基于FC算法进行改进的HFC算法能在各种环境下得到一个较好的划分，并且能够大幅度地减少所使用的时间。例如在ami49中，IP单元片的数量为49，而HFC算法能够很好地处理该超大规模集成芯片。

可以很容易地观察到在运行时间的效率上FC算法和基于FC算法的改进算法HFC要优于原有的两种粗化算法。

另一个衡量算法性能的重要指标为该芯片的吞吐量。在本文实验中将选取3个最优的划分进行吞吐量的计算，并且统计该3个划分的平均吞吐量，具体数值如图6所示。

Fig.6　Comparison of throughput with differentcoarsening algorithms for 3D NoCs图6 不同粗化算法的3D NoC吞吐量

从图6中可以看出，各个算法在xerox用例中的吞吐量都较小，而在apte上的吞吐量相对较大，对于ami25，相比于EC算法，改进的FC算法反而降低了网络的吞吐量，但随着IP单元片数目的递增，FC算法比EC算法的吞吐量更大。

然而，相比于HEC算法，EC和FC算法在对于网络吞吐量上性能大大优于HEC算法，在各个数据集上的吞吐量都高于HEC算法。而FC相对于EC算法在网络吞吐量上得到了更大的提升。综上所述可以得出，针对网络平均吞吐量经过优化后的粗化算法FC要略微优于EC算法，并且相对于HEC算法有较大的提升。

基于FC算法的HEC算法比原FC算法有着更好的划分。在吞吐量上也比上述3种粗化算法更加高效。

4.3迁移优化阶段算法对性能的影响

本节将基于不同迁移优化阶段的算法对片上网络的运行时间和吞吐量进行比较分析。

表2的结果表明，在片上网络的运行时间方面，基于跳出局部最优的1-way FM算法相对于EEFM算法有较大的改进，而相对于FM算法只有较少的提升。对于IP单元片数目较少的集成网络，1-way FM算法相对于其他两种算法，所提升的性能并不是太大，但是一旦所处理的集成网络规模巨大，可以看到基于1-way FM算法的网络能够大大地减少片上网络所运行的时间。

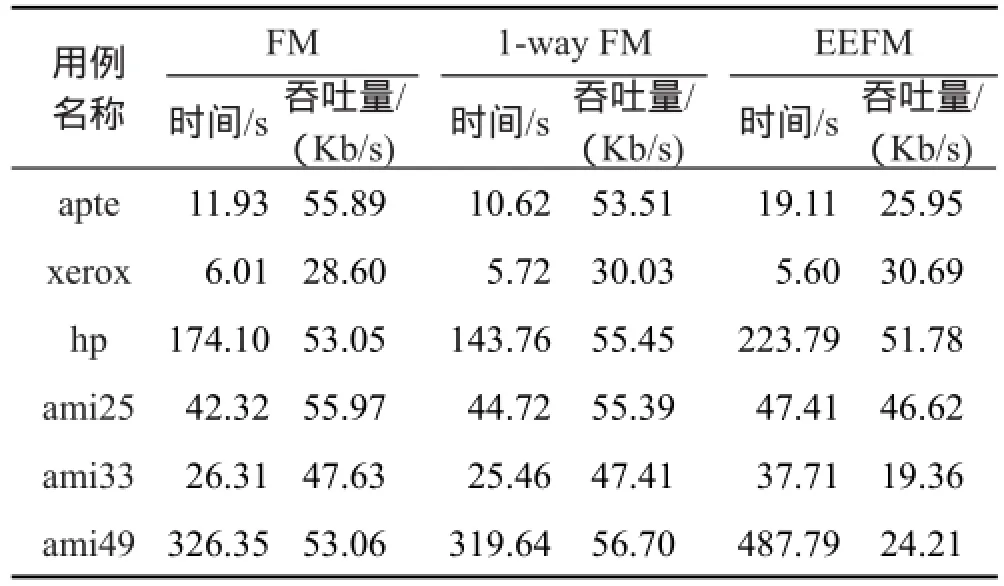
Table 2　Impact of different migration optimization algorithms for 3D NoCs表2　不同迁移优化算法在片上网络的影响

在片上网络的吞吐量方面，可以得出和上述运行时间相同的结论，即1-way FM算法相对于EEFM算法有着较好的性能提升，而相对于FM算法，提升的幅度并不大。然而可以发现，一旦所处理的网络规模变得十分巨大，基于EEFM算法的片上网络的吞吐量变得十分小。因此可以得出结论，EEFM算法并不能够很好地处理巨大规模的片上网络。相反，1-way FM算法能够在较大规模集成网络上保持较好的性能。但也需要注意的是1-way FM算法的高性能是以增加算法复杂度为代价的。

4.4hMetis算法框架对性能的影响

根据表3、表4得出若干结论：在时间性能方面，对于不同的测试数据集可以得到不同的hMetis算法框架来对该数据集进行划分，所得到的最优划分如表中所示。例如对于apte这个数据集，可以在粗化阶段使用HEC粗化算法对其进行粗化，并且在迁移优化阶段使用FM算法来进行优化，从而能得出该电路较好的hMetis算法框架。而该电路的最优划分所需要的时间为43.07 s（参见表3），而具有较好性能的算法框架为HFC+1-way FM。

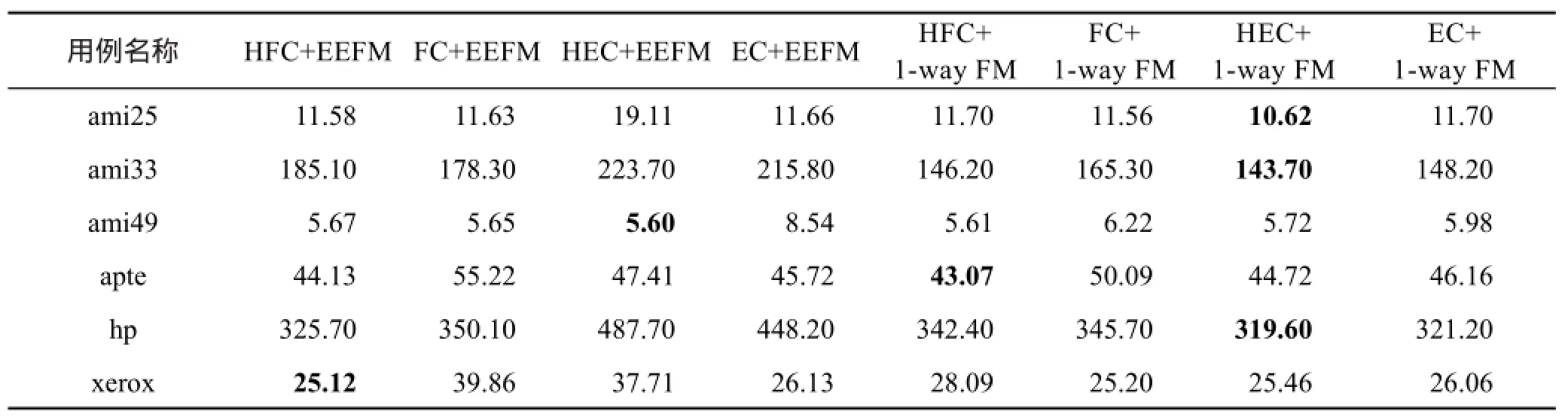
Table 3　Comparison of CPU time with different algorithms used at different phases表3　不同阶段不同算法所使用的CPU时间　s

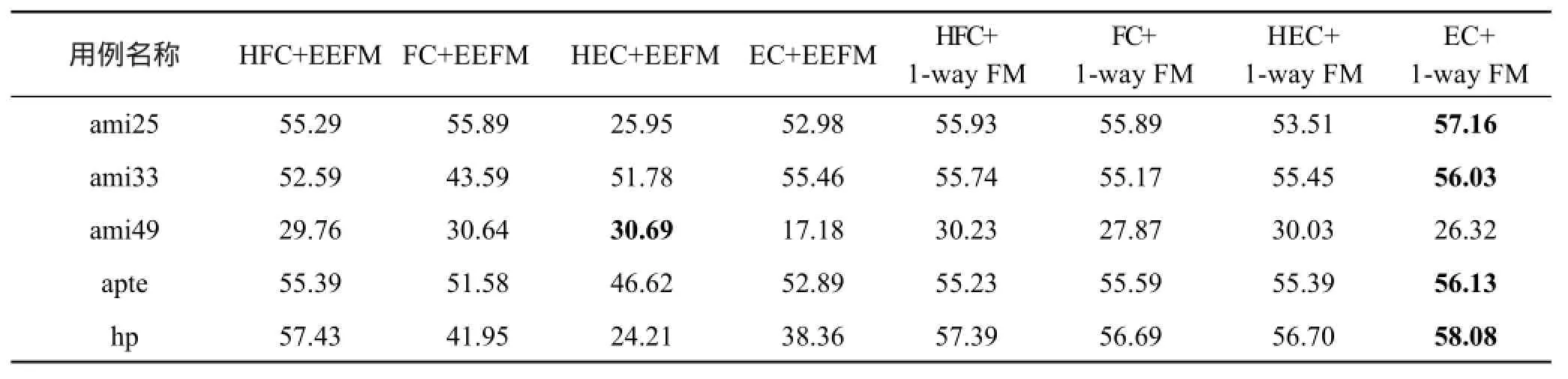
Table 4　Comparison of network throughput with different algorithms used at different phases表4　不同阶段不同算法网络的吞吐量大小　Kb/s

与上述时间性能方面的计算方式相同，在对吞吐量进行评估比较时，对于不同的数据集，也会有相应的最优划分来得到一个较大吞吐量的划分框架（参见表4）。例如apte数据集的最大吞吐量为56.13 Kb/s，所得到的较优hMetis框架算法为EC+1-way FM。

5　结束语

本文研究了针对异构三维片上网络设计的一种超图划分框架，并且对现有的超图划分中每一步骤中算法进行分析与改进。在粗化阶段，提出常见的粗化算法的不足之处，并且对其进行修改，提高片上网络的性能；在迁移优化阶段，对FM算法进行改进，并且对不同的细化算法进行比较分析。最后将不同的粗化细化算法进行实验比较分析，得出一个较好的基于hMetis的算法框架。然后将得到的较好的hMetis框架算法应用到异构三维片上网络中，分析该算法的性能效果，并且使用运行时间和网络吞吐量的性能指标来衡量利用该算法框架设计的三维片网性能的优劣。

由于本文使用的细化阶段算法为1982年Fiduccia和Mattheyses提出的FM算法，经过三十多年，虽然该领域内提出了许多图划分的算法，但基本上都以此算法为基础而进行的改进。因此，寻找一种更好的划分来提高片上网络的性能将是下一步的工作。另外，由于本文所研究的片上网络性能指标只有网络的运行时间和吞吐量，但真正的片上网络受许多因素的影响，下一步还可以用其他更多的影响因素来衡量算法的优劣。

References:

[1]Lu Yue,Cao Jianwen.Multilevel hypergraph partitioning and multi-phase refinement[J].Computer Engineering and Design,2009,30(4):800-802.

[2]de Paulo V,Ababei C.A framework for 2.5D NoC exploration using homogeneous networks over heterogeneous floorplans[C]//Proceedings of the 2009 International Conference on Reconfigurable Computing and FPGAs,Cancun,Mexico, 2009.Washington,USA:IEEE Computer Society,2009: 267-272.

[3]de Paulo V,Ababei C.3D network-on-chip architectures using homogeneous meshes and heterogeneous floorplans[J].International Journal of Reconfigurable Computing,2010(1):1.

[4]Kernighan B W,Lin S.An efficient heuristic procedure for partitioning graphs[J].The Bell System Technical Journal, 1970,49(2):291-307.

[5]Fiduccia C M,Mattheyses R M.A linear-time heuristic for improving network partitions[C]//Proceedings of the 19th IEEE Conference on Design Automation,Las Vegas,USA, Jun 14-16,1982.Piscataway,USA:IEEE,1982:175-181.

[6]Karypis G,Kumar V.METIS 3.0:unstructured graph partitioning and sparse matrix ordering system,Technical report 97-061[R].1997.

[7]Karypis G,Kumar V.A fast and highly quality multilevel scheme for partitioning irregular graph[J].SIAM Journal on Scientific Computing,1998,20(1):359-392.

[8]Karypis G,Kumar V.Multilevel k-way hypergraph partitioning[C]//Proceedings of the 36th Annual ACM/IEEE Design Automation Conference,New Orleans,USA,1999. New York,USA:ACM,1999:343-348.

[9]Wang Miao,Tang Yuhua.Design and implementation of parallel graph-partitioning and hypergraph-partitioning methods for OpenFOAM[D].Changsha:National University of Defense Technology,2012.

[10]Karypis G,Aggarwal R,Kumar V,et al.Multilevel hypergraph partitioning:applications in VLSI domain[J].IEEE Transactions on Very Large Scale Integration Systems, 1999,7(1):69-79.

[11]Karypis G,Kumar V.Analysis of multilevel graph partitioning [C]//Proceedings of the 1995 IEEE/ACM SC95 Conference on Supercomputing,San Diego,USA,Dec 4-8,1995.Piscataway,USA:IEEE,1995:29.

[12]Cai Wenzan,Young E F Y.A fast hypergraph bipartitioning algorithm[C]//Proceedings of the 2014 IEEE Computer Society Annual Symposium on VLSI,Tampa,USA,Jul 9-11, 2014.Piscataway,USA:IEEE,2014:607-612.

[13]Zhao Zhizi,Tao Lixin,Zhao Yongchang.An effective algorithm for multiway hypergraph partitioning[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,2002,49(8):1079-1092.

[14]Flajolet P,Martin G N.Probabilistic counting algorithm for data base applications[J].Journal of Computer and System Sciences,1985,31(2):182-209.

[15]Huang Yuchi,Liu Qingshan,Lv Fengjun,et al.Unsupervised image categorization by hypergraph partition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(6):1266-1273.

附中文参考文献:

[1]卢玥,曹建文.超图多级划分算法框架及对划分结果的多阶段优化[J].计算机工程与设计,2009,30(4):800-802.

[9]汪淼,唐玉华.面向OpenFOAM的并行图划分与超图划分方法设计与实现[D].长沙:国防科技大学,2012.

SONG Guozhi was born in 1977.He received the Ph.D.degree in electronic engineering from Queen Mary University of London in 2009.Now he is an associate professor and M.S.supervisor at Tianjin Polytechnic University.His research interests include 3D network-on-chip,heterogeneous wireless network integration and wireless sensor networks,etc.

宋国治（1977—），男，黑龙江哈尔滨人，2009年于英国伦敦大学玛丽王后学院电子工程专业获得博士学位，现为天津工业大学副教授、硕士生导师，主要研究领域为三维片上网络，异构无线网络整合，无线传感器网络等。发表学术论文40余篇，获发明专利6项，软件著作权1项，主持或参加过多项国家自然科学基金、国家科技支撑计划及天津市教委项目等。

ZHANG Dakun was born in 1960.She received the Ph.D.degree in computer application from Northeastern University in 2004.Now she is a professor and M.S.supervisor at Tianjin Polytechnic University.Her research interests include 3D network-on-chip,combinational algorithm and virtual reality technology,etc.

张大坤（1960—），女，辽宁阜新人，2004年于东北大学计算机应用专业获得博士学位，现为天津工业大学计算机科学与软件学院教授、硕士生导师，主要研究领域为三维片上网络，组合算法设计，虚拟现实技术等。发表学术论文30余篇，主持并承担过多项国家自然科学基金、国家863计划及省部级课题。

MA Jiechao was born in 1991.He is a postgraduate student at Sun Yat-Sen University.His research interests include 3D network-on-chip and hyper-graph partition,etc.

马杰超（1991—），男，浙江宁波人，中山大学硕士研究生，主要研究领域为三维片上网络，超图划分等。

TU Yao was born in 1992.He is a postgraduate student at School of Computer Science and Software Engineering, Tianjin Polytechnic University.His research interest is 3D network-on-chip floorplanning.

涂遥（1992—），男，安徽淮南人，天津工业大学计算机科学与软件学院硕士研究生，主要研究领域为三维片上网络布局规划问题。

LIU Chang was born in 1994.She is a student at School of Computer Science and Software Engineering,Tianjin Polytechnic University.Her research interest is 3D network-on-chip floorplanning.

刘畅（1994—），女，黑龙江大庆人，天津工业大学计算机科学与软件学院学生，主要研究领域为片上网络的布局划分。

*The National Natural Science Foundation of China under Grant No.61272006(国家自然科学基金);the National Training Program of Innovation and Entrepreneurship for Undergraduates under Grant No.201510058050(国家级大学生创新创业训练计划项目).

Received 2015-06,Accepted 2015-08.

CNKI网络优先出版:2015-08-12,http://www.cnki.net/kcms/detail/11.5602.TP.20150812.1652.010.html

+Corresponding author:E-mail:guozhi.song@gmail.com

文献标志码：A

中图分类号：TP393.0

doi:10.3778/j.issn.1673-9418.1507041

Hyper-Graph PartitionAlgorithms for Heterogeneous 3D Network-on-Chip Floorplanning Optimizationƽ

SONG Guozhi+,ZHANG Dakun,MAJiechao,TU Yao,LIU Chang
School of Computer Science&Software Engineering,Tianjin Polytechnic University,Tianjin 300387,China

Abstract:Network-on-chip(NoC)is a feasible technology with a large number of embedded cores integrated into a single wafer.Compared with the traditional system-on-chip,it can better meet the challenges of the future need for more large-scale integration of the kernel,resulting in a wider range of applications.However,most of the research is based on homogeneous architecture assuming that all the tiles have the same area.But this assumption is not realistic. Therefore,the research on heterogeneous 3D NoCs is very necessary.With heterogeneous 3D NoCs,a reasonable division of network elements has a significant impact on the performance of heterogeneous 3D NoCs.This paper firstly describes the floorplanning based on 3D NoC of heterogeneous network architecture,and maps VLSI(very large scale integration)into a hyper-graph,then divides the hyper-graph into multi-levels.Secondly,this paper introduces varivarious of common algorithms in the different phases,analyzes the potential problems of the algorithms,and puts forward several new algorithms to improve the performance of NoC.Finally,a number of simulation experiments are conducted based on a few conventional VLSI data sets to compare the performance of the different phases with different algorithms and choose the best hMetis algorithm framework on the data sets.

Key words:3D network-on-chip;heterogeneous floorplanning;hyper-graph partition;hMetis