嵌入共轭梯度的二次学习教与学优化算法*

王培崇，彭菲菲，钱　旭1.河北地质大学 信息工程学院，石家庄 05001.中国矿业大学（北京）机电与信息工程学院，北京 10008.北京邮电大学 图书馆，北京 10008



嵌入共轭梯度的二次学习教与学优化算法*

王培崇1,2+，彭菲菲3，钱旭2
1.河北地质大学 信息工程学院，石家庄 050031
2.中国矿业大学（北京）机电与信息工程学院，北京 100083
3.北京邮电大学 图书馆，北京 100083

WANG Peichong,PENG Feifei,QIAN Xu.Improved teaching-learning based optimization algorithm with conjugate gradient methods and second study.Journal of Frontiers of Computer Science and Technology, 2016,10(6)：891-900.

CNKI网络优先出版:2015-11-24,http://www.cnki.net/kcms/detail/11.5602.TP.20151124.1414.006.htmland GL(Gaussian learning)will be executed to them.Finally,some experiments on test functions show that the improved TLBO algorithm has higher precision and better global convergence than TLBO,fitting to solve higher dimension optimization functions.

摘要：教与学优化算法通过模拟自然班的教与学行为实现复杂问题的求解，已经得到较为广泛的应用。为了克服该算法容易早熟，解精度低的弱点，提出了一种改进的混合混沌共轭梯度法教与学优化算法。改进算法应用Chebyshev混沌映射初始化种群，以提高初始种群对解空间的覆盖。为了保持种群多样性，引入动态学习因子，使学生个体能够在早期主要向教师学习，并逐渐提高个人知识对其进化的影响比例。每次迭代后，教师个体将执行共轭梯度搜索。种群内适应度较差的学生个体如果长时间状态难以改变，则基于反向学习和高斯学习进行二次学习优化。最后在多个典型测试函数上的实验表明，改进算法对比相关算法具有较佳的全局收敛性，解精度较高，适用于求解较高维的函数优化问题。

关键词：教与学优化算法；Chebyshev映射；动态自适应学习；共轭梯度法；二次学习

ISSN 1673-9418CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(06)-0891-10

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

1　引言

2012年印度学者Rao等人[1]通过研究、模拟班级的群体学习现象，提出了一种新颖的演化算法——教与学优化（teaching learning based optimization，TLBO）算法[1-2]。在该算法中，执行演化的种群被划分为教师和学生两类。教师是种群内适应度最佳个体，教师通过“教”对学生进行教学，学生通过“学”实现学生间的相互学习。该算法由于原理简单，容易理解，参数较少，一经提出即吸引了较多学者围绕它展开相关研究，并被成功应用于神经网络的参数优化[3]、热点冷却器优化和热交换器优化[4]、平面钢框架的设计优化[5]、电力系统经济负荷调度问题[6]、机械设计优化问题[7]、烯裂解炉裂解运行效益优化[8]等领域。

研究表明，TLBO算法在求解较低维度函数时，表现出较好的求解效果，而在求解高维问题时，往往容易出现早熟，解精度较低等现象[9]。为了克服算法的这些弱点，Rao等人提出了一种精英教学优化算法（elitist TLBO，ETLBO）[9]，每次迭代前，利用精英个体替换种群内的最差个体，同时通过变异机制删除重复的学生个体。文献[10]提出了一种带有交叉操作的教与学优化算法（cross-TLBO，C-TLBO），即在TLBO算法中引入遗传算法中的交叉操作，将“教”和“学”两个阶段进行了有效融合，算法的局部搜索得到增强，平衡了算法的开采和勘探能力。Rajasekhar等人提出了一种相对精英教学优化算法（opposite ETLBO，OETLBO）[11]，有效避免了种群容易聚集在局部最优个体周围的弱点，在算法后期能够较好地保持种群多样性。于坤杰等人[12]在ETLBO算法基础上增加了针对快速提升较差学生分数的精英反馈机制，利用精英个体的较强引导能力，加快种群的收敛速度，提升了算法的精度。

为了改善TLBO的全局收敛能力，提高解精度，本文对标准TLBO进行了如下4个方面的改进。首先，利用Chebyshev混沌[13]机制的初始化种群，提高种群对解空间的覆盖率。第二，为了体现学生学习知识过程的动态性，引入一个动态自适应因子，使算法早期学生主要向教师学习，快速提升自己的能力，后期逐渐增加自身知识对其进化的影响。第三，为了加强对最优解空间的局部搜索，以教师个体所在点为起始点，执行共轭梯度[14]搜索。第四，种群内的部分劣质个体，如果经过多次迭代之后仍然难以提高，则应用反向学习（opposition-based learning，OBL）[15]和高斯学习（Gaussian learning，GL）[16]对其进行二次强化学习，使其跳出局部极值的约束。

2　标准教与学优化算法

假设问题的解空间为D维，将班级内的教师和学生看作待求解问题的候选解，标准TLBO算法就是将优化问题求解看成是在该D维空间内的一个搜索过程。班级内每一个人所具有的知识被看作一个可能的候选解，相应解的适应度对应知识的质量。

不失一般性，以最小化问题minf(x1,x2,⋅,xn)为研究实例，其中xi∈[Lj,Uj]，1≤j≤n。标准教与学优化算法，首先在解空间内随机初始化产生N个个体，组成教学班级。完成种群初始化，最大迭代次数等设置后，算法进入迭代演化过程。该算法包含3个基本操作。

（1）以式（1）在解空间进行种群初始化。

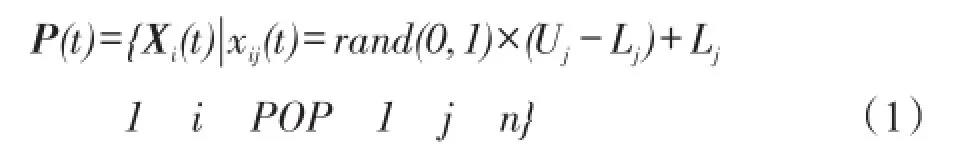
其中rand(0,1)为(0,1)上的随机数，xi∈[Lj,Uj]。

（2）教师教学阶段。计算班级内全部个体的平均值 Xmean(t)，设教学因子为 β=round(1+rand(0,1))（注：round()为四舍五入），对种群中所有个体执行式（2）生成其子个体的第d维，并以优胜劣汰的方式更新Xi(t)。

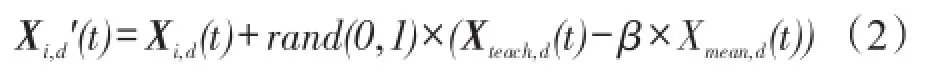
（3）学生互相学习阶段。从种群中随机选择两互不相同的个体Xr1(t)、Xr2(t)，令个体Xi(t)向其中优秀的个体进行学习。以式（3）生成子个体，同样优胜劣汰更新Xi(t)。

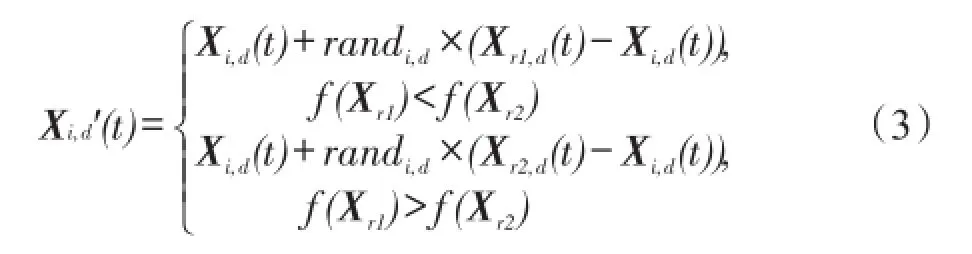
3　TLBO算法的改进

影响TLBO算法早熟的主要原因之一是所求问题的解空间分布。由于种群数量有限，且分布具有一定的随机性，对于较复杂的问题而言，当前优质解的收敛方向不一定就是全局最优解的收敛方向。求单峰问题中，下面两种情况容易发生算法的提前收敛。第一，最优解区域附近种群个体适应度跨度变化较大；第二，最优个体和次优个体的适应度相差较小。而在多峰问题中，如果解与解之间相距较远，也很难保证种群能够覆盖到全部最优区域。

在实际应用中，为了保证运算速度，种群规模设置有限，种群中个体采用随机初始化产生，故种群所覆盖的解空间存在不确定性。在初始种群没有覆盖到全局最优解的情况下，如果在有限迭代次数内，无法搜索到最优解所在区域，则算法早熟是难以避免的。因此，为了改善算法的性能，一方面要提高种群的多样性，扩大搜索范围；另一方面要加强对最优解所在区域的搜索，平衡全局搜索与局部搜索。

3.1Chebyshev混沌种群初始化

大自然中的混沌现象，是一种确定性系统中存在的随机状态，具有非常强的遍历性、随机性和规律性。混沌行为本质上是由确定性的规则导致，对初始条件敏感，为无固定周期的一种长期行为。在一定范围内，混沌行为能够使个体不重复地遍历自身所有状态。常见的混沌扰动方程为Logistic方程和Chebyshev映射。Chebyshev映射的方程为式（4）。

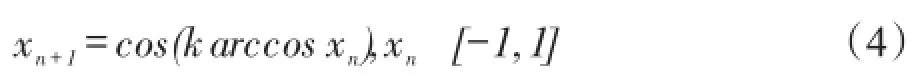
式中取k≥2，无论初始值的选择如何，迭代产生的数据序列均不会相交。相关研究表明，Chebyshev映射的分布范围较广，能够比较均匀地分布在[-1,1]区间上。因此，采用Chebyshev映射机制初始化的种群，分布会比较均匀且覆盖广泛。改进TLBO算法中应用Chebyshev混沌映射产生初始化种群，方法如下所述。

3.2学生的动态自适应学习

在学生进行学习的过程中，学生自身所具有的知识和教师的“教”行为共同对该学生自身状态的提高产生影响。在初始阶段，学生本身的知识较少，比较多地受到教师“教”行为的影响，而随着学生不断的学习，自身知识的提升，教师的“教”行为往往对学生知识素质的提升逐渐减少。但是，标准TLBO算法中学生自身状态的进化通过式（2）来实现，并没有体现这一学习过程。为了体现这一学习过程，本文在式（2）中引入一个动态学习因子ω。改进后的教师“教”行为见式（5）。

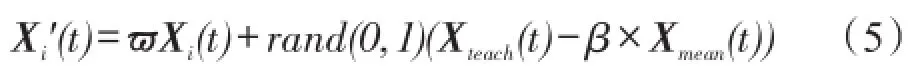
考虑公式中的比例因子ω∈[ωmin,ωmax]动态变化，并且应该与算法迭代次数有关，设置其依据式（6）进行变化。

其中,ωstart、ωend是该因子的变化范围。

通过式（5）可以看出，在算法迭代初期，由于ω因子较小，种群中的学生个体主要是向教师学习，由于教师是种群内的最优个体，种群迅速向教师个体所在空间靠近。随着迭代的进行，ω逐渐增加，学生个体自身知识在其进化过程中所占比例不断增加，算法种群多样性保持较好，避免学生群体过早聚集于教师周围，造成算法早熟。

3.3教师的共轭梯度搜索

最初的共轭梯度法主要用于求解正定系数矩阵的线性方程组。后来，在基本共轭梯度法基础上，Fletcher和Reeves对该方法进行了改进和完善，使得该算法能够用于求解大型非线性无约束最优化问题[14]。在该方法中，主要应用目标函数的一阶导数信息，通过多次迭代对某个节点的周围进行搜索，既克服了最速下降法收敛速度慢的弱点，又有效克服了牛顿迭代法需要存储和计算Heslan矩阵及求逆的缺点，能够快速收敛到所求问题的最优解。

算法1共轭梯度法（conjugate gradient method, CGM）

输入：初始点X0，精度eps。

输出：最优点Xk+1。

步骤1迭代次数计数器t=0，初始搜索方向d0=-g0。

步骤3计算ak和Xk+1，使得式（7）成立：

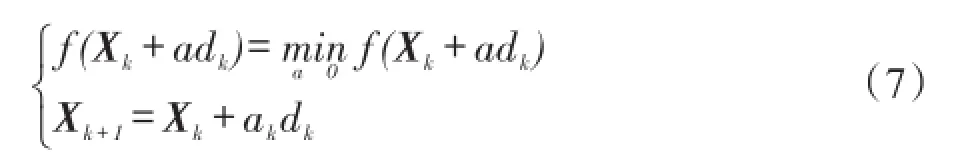
步骤4应用Fletcher和Reeves方法计算dk+1：

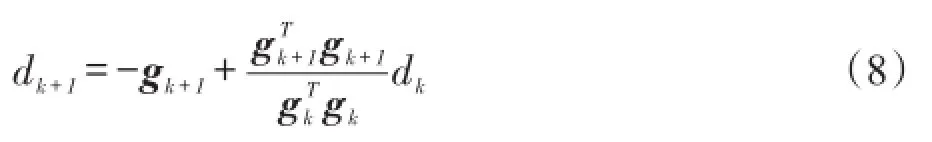
步骤5令t=t+1，goto步骤2。

在TLBO算法中，教师个体Xteach(t)一定程度上代表了种群的前进方向，由TLBO算法原理可以看出，学生个体通过式（2）、（3）学习进化，一方面向Xteach(t)所在空间靠近，一方面通过互相学习保持种群多样性。但是TLBO算法一个明显的缺点是教师个体缺少学习机制，即没有对教师Xteach(t)所在空间进行精细的局部搜索。以最小化minf(x)示例，如果使教师个体按照下降的方向进行搜寻，将会提高算法的效率。共轭梯度算法恰好能够按照负梯度方向寻找下一个结点，因为负梯度方向是个体的下降方向，所以寻找到的结点要优于初始结点。

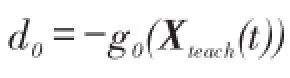
共轭梯度法局部搜索能力强，但是该算法搜索到的最优点不一定是全局最优点。因此为了提高算法的整体效率，设置共轭梯度算法的终止条件为两种：第一种是解的精度。但是考虑在某些问题的求解过程中，即使设置较低的精度要求，共轭梯度算法的迭代次数仍然很高，因此算法的第二个终止条件是设定固定的迭代次数。搜索完毕后，直接应用所得到的点Xk+1替换教师个体Xteach(t)。

3.4劣质个体的二次强化学习

观察TLBO的原理，可知TLBO算法通过应用班级的平均值与教师的差引导种群的进化，提升种群的平均值。

在实际算法运行过程中，观察到在求解高维的多峰函数优化时，存在部分劣质个体经过多次迭代学习后，仍然难以进化，或者进化幅度非常低，影响种群平均值的快速提高。这与现实的学习过程中，班级中通常会存在个别学生难以提升有相似性。针对此现象，通常会对学习较差的学生采取多种方法进行辅导，以提升这些学生的素质。

本文为了提高劣质个体的进化能力，改善其自身的状态，加速算法收敛，对这些长时间没有得到提高的劣质个体采取两种学习机制进行二次学习，然后基于模拟退火机制进行轮盘赌选择学习后的新状态。

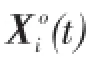
定义1[15]（反向解）设在区间[a,b]上存在一个实数x，则x的反向数定义为x′=a+b-x。鉴于此，假设在R域上存在某N维点X=(x1,x2,⋅,xi,⋅,xN)，并且xi∈[ai,bi]，则定义X′=(x1′,x2′,⋅,xi′,⋅,xN′)为X的反向点。其中，xi′=k×(ai+bi)-xi，k为[0,1]之间分布均匀的随机数，称作一般化系数。

算法2反向学习算法（OBL）

输入：个体Xi(t)，限制区间[a,b]，最大迭代次数Itermax。

步骤1设置迭代次数为t=0。

步骤2生成一般化系数k∈[0,1]，依据定义1生成反向解Xt′(t)。

步骤3迭代次数没有满足结束条件，则t=t+1, 并goto步骤2。

借鉴参考文献[16]中的高斯学习概念。

定义2[16]（高斯学习）设D是问题的解空间维数，则个体Xi(t)在d维上的高斯学习定义：

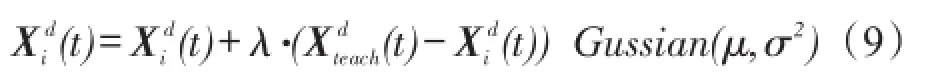
Gussian(μ,σ2)产生一个服从高斯分布的随机数，均值为μ，方差为σ2，λ∈(0,1)。

教师是种群中的最优个体，一定程度上代表了种群的演化方向，因此模拟退火的选择机制设置如下。

设当前温度是k，则可以通过式（10）得到某个体Xi(t)对于教师个体Xteach(t)的突跳概率，并利用式（11）得到Xi(t)替换Xteach(t)的概率。

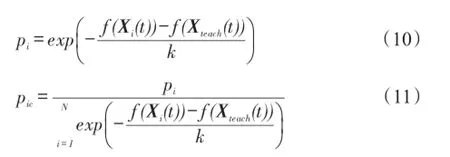
基于替换概率pic以轮盘赌方式选择一个个体更新Xi(t)。

为了提高算法效率，本文设定为每隔100代，针对种群中的最差个体进行一次检查，当该个体的变化幅度低于阈值σ=0.01时执行二次强化学习。

3.5改进算法的步骤

算法3 CCGTLBO（chaotic and conjugate gradient TLBO）

输入：个体X0(0)，种群数目N。

输出：最优个体Xgbest(t)。

步骤1以X0(0)为起点，依据式（4）进行迭代，直至产生N个个体，组成初始种群POP(0)，迭代计数器t=0。

步骤2在种群中搜索适应度最佳个体，设为教师Xteach(t)，并计算班级的平均值Xavg(t)。

步骤3依据式（5）进行教师的“教”行为。

步骤4依据式（3）实现学生的互相“学”行为。

步骤5对教师个体Xteach(t)实施共轭梯度算法搜索。

步骤5.1设定共轭梯度算法的相应参数，迭代次数k=0；

步骤5.2如果满足共轭梯度法终止条件，goto步骤6；

步骤5.3a=1；

步骤5.5应用Fletcher和Reeves方法计算dk+1，k=k+1，goto步骤5.2。

步骤6更新教师个体Xteach(t)=Xk+1。

步骤7种群内的最差个体在100次迭代后，如果其变化幅度小于指定的阈值σ，则对其执行3.4节中设定的二次强化学习，否则goto步骤8。

步骤8算法满足结束条件，则输出Xgbest(t)，结束算法；否则goto步骤2。

4　仿真实验与分析

4.1实验1

将CCGTLBO算法应用C语言编程实现，在VC6的环境下编译运行，以测试算法的性能。计算机的硬件配置是AMD Turion64双核CPU，2.0 GHz主频，2 GB内存。测试函数选择6个经典Benchmark[12]函数，其中包括 f1-Sphere、f2-Rosenbrock、f3-Schwefel、f4-Rastrigin、f5-Ackley、f6-GireWank，分别测试6个函数的30维和100维度两个维度，以验证改进算法在低维度和高维度两种情况下的求解性能。参与对比的算法包括TLBO、ITLBO[17]（improved TLBO）、ETLBO、AFSA[18]（artificial fish swarm algorithm）等。CCGTLBO的种群设置为20，迭代次数设为1 000，嵌入的共轭梯度搜索的迭代次数是100，精度为0.001，自适应学习算子上下界限是λstart=0.1，λend=1.5。ITLBO、ETLBO两个算法的参数设置遵循相关文献。AFSA算法的参数设置如下：鱼群规模 fish_number= 20，视野范围visual=5，移动步长step=1，拥挤度因子delta=0.5，尝试次数try_number=3，迭代次数itermax=1 000。

为体现公平，减少算法的偶然性所带来的误差，将上述参与对比的算法分别独立运行30次，取它们的解平均值及解标准差，求解结果列于表1。在表2中列出了5个算法在测试函数上收敛成功的次数、平均收敛代数、运行时间等指标。因为AFSA算法在所有的测试函数上均没有成功收敛，所以表2中只给出了TLBO以及相关算法的数据。

观察表1、表2中的数据，人工鱼群算法的表现较TLBO算法的解精度相差较多，在全部6个测试函数上都没有找到最优解，但是人工鱼群算法解的标准差相比较TLBO算法并不低多少，尤其在单峰的 f1函数上，AFSA算法的解标准差还要比TLBO算法优秀，说明人工鱼群算法要比TLBO稳定，亦是一个优秀的演化算法，在解精度要求不高的情况下可以用来快速获得可行解。

在 f1函数的维度为30时，CCGTLBO算法正确找到了函数的最优解，而参与对比的ETLBO、ITLBO、TLBO算法均没有找到全局最优解。函数维度为100时，4个算法均没有在迭代次数内寻找到全局最优解，但是CCGTLBO算法的精度是最高的，要远远超过其他3个算法。 f2函数在局部极值附近存在陡峭的峡谷，4个算法均没有找到最优值。但是CCGTLBO算法的解精度、标准差仍然是最好的。注意到这4个算法，在30维的结果与100维的结果几乎都是一个数量级，变化很小，说明在求解 f2函数时，TLBO系列算法较难克服局部极值的约束，解精度较低，需要引入其他优秀的演化算法机制进行改进。函数 f3是一个单峰函数，主要用于对比算法的解精度。在两种维度上，改进后的3个算法均较为轻松地寻找到了全局最优值，较标准TLBO算法有较大幅度提高。对比表2中所列出的3个算法的其他指标，CCGTLBO算法收敛成功的迭代次数要小于ETLBO、ITLBO算法。函数 f4同样是一个多峰函数，存在较多的极值点，需要算法具有较好的跳出局部极值约束的能力。与 f3函数的结果一样，改进后的3个算法均找到了全局最优值，CCGTLBO算法在该函数上的表现是最好的，所需迭代次数最少。在多峰的 f5函数上，参与对比的算法均没有找到全局最优值，在30维时，CCGTLBO算法的求解结果甚至稍劣于ETLBO算法，与ITLBO算法基本相当。但是当函数维度升为100时，CCGTLBO算法的求解结果较30维时基本没有下降，而ETLBO、ITLBO算法均有所下降，说明CCGTLBO算法的稳定性要更好一些。另外，其成功收敛的次数是最多的，且所需平均收敛代数最少。 f6函数也是一个多峰函数，CCGTLBO算法的表现优异，与ETLBO、ITLBO算法一样都成功收敛30次，找到了函数的全局最优解，并且所需迭代次数较少。

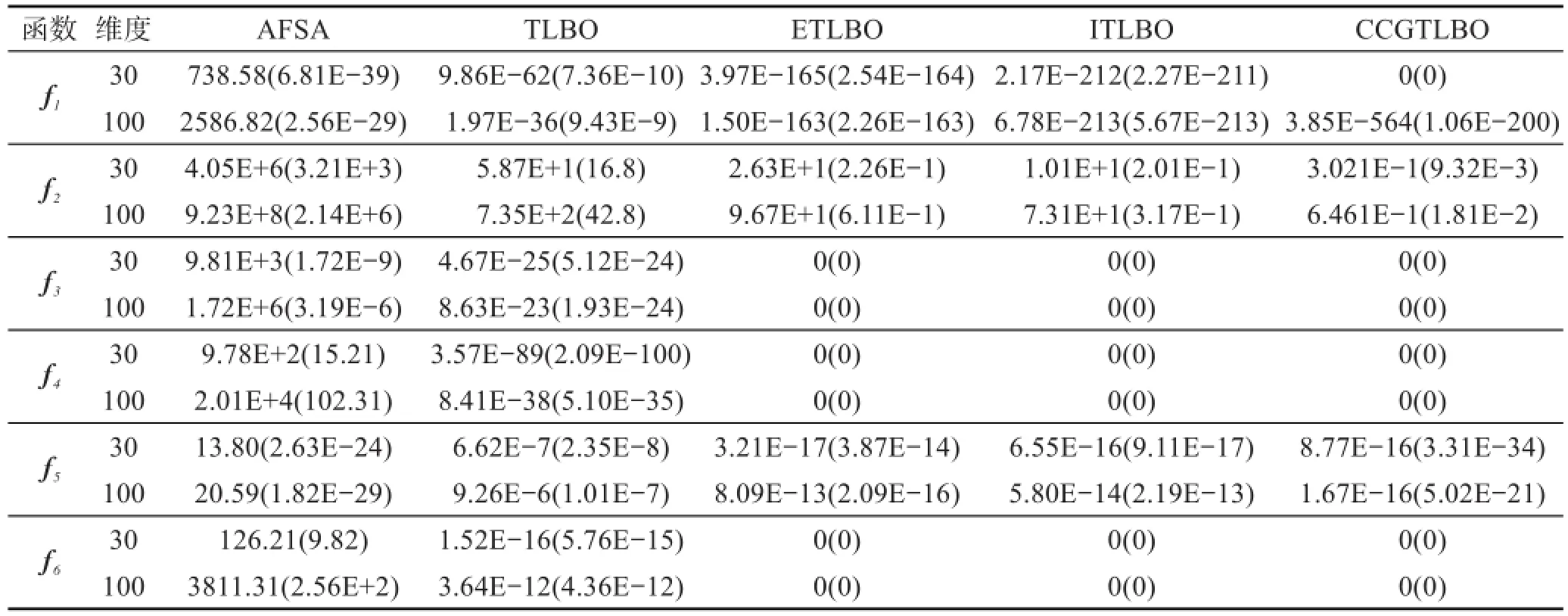
Table 1　Comparison of mean for unconstrained benchmark functionsf1～f6(Std)表1　无约束测试函数 f1～f6上的结果平均值对比（标准差）

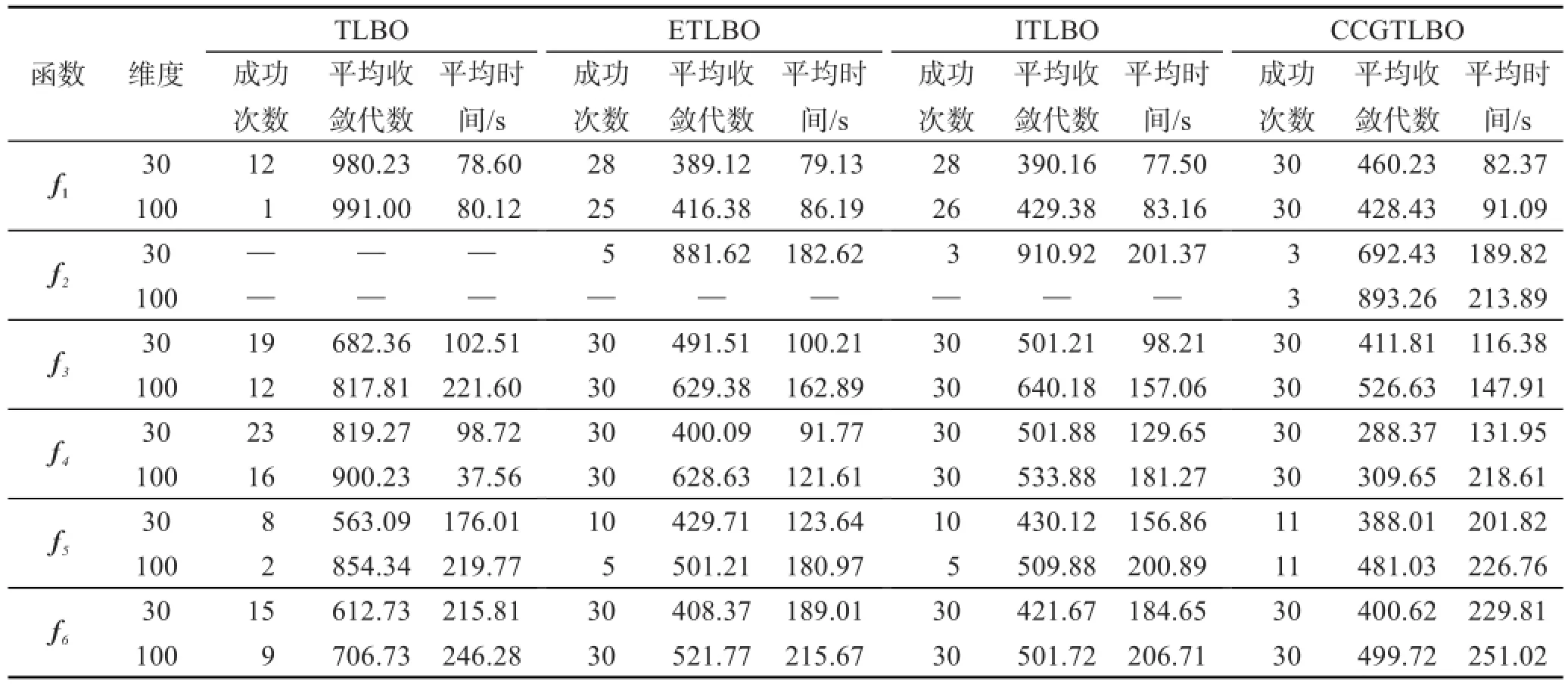
Table 2　Success number,average convergence iterations and average time for unconstrained benchmark functionsf1～f6表2　无约束测试函数f1～f6上成功次数、平均收敛代数、平均时间

为了更直观地观察算法在函数上的收敛效果，绘制了其中4个算法分别在 f1、f2、f5、f6上的收敛曲线，如图1、图2、图3、图4所示。从4个图展示的收敛曲线可以看出，本文提出的CCGTLBO算法在4个函数上，均能够快速收敛。在 f1函数上，CCGTLBO、ITLBO、ETLBO算法的收敛曲线基本一致，较TLBO算法收敛到全局最优值更加迅速。

在另外的3个算法上，标准TLBO算法的收敛曲线比较缓慢，尤其是在 f2函数上还有跳跃，而3个改进算法收敛曲线比较平滑，尤其是CCGTLBO算法的收敛曲线更为平稳，能够快速收敛。

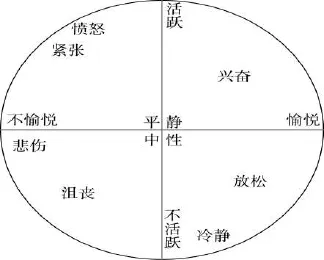
Fig.1　Convergence curves off1图1　f1函数上的收敛曲线

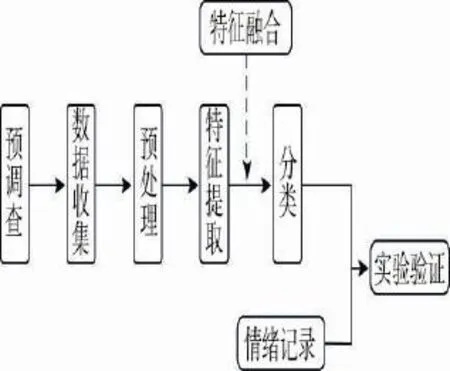
Fig.2　Convergence curves off2图2　f2函数上的收敛曲线

Fig.3　Convergence curves off5图3　f5函数上的收敛曲线

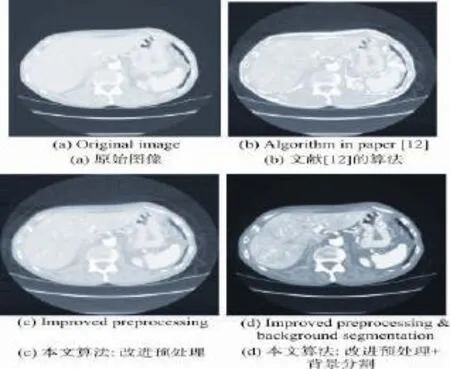
Fig.4　Convergence curves off6图4　f6函数上的收敛曲线

从上面的分析可以看到，CCGTLBO算法的解精度在所测试的6个函数上，较TLBO算法有较大提高，尤其在TLBO算法表现较差的高维度函数上，优势更加明显。在大部分的函数上，也较ETLBO、ITLBO两个算法优秀。在时间的对比上，CCGTLBO算法相比较其他算法不占优势，几乎所有测试函数所需时间均是最长的。主要是因为该改进算法中融入了多种改进机制和相关算法，增加了整个算法的计算时间。综合考虑，该算法仍然可以认为是一个优秀的算法，对TLBO的改进是成功的。

4.2实验2

继续选择两个非线性方程进行测试，以检测改进后算法的可行性及其优势，所选择的两个测试实例分别来自实际工程和科学计算领域。在这项测试中，选择了TLBO和CCGTLBO两个算法，并分别独立执行50次，算法的参数设置同实验1。对比结果见表3。

例1

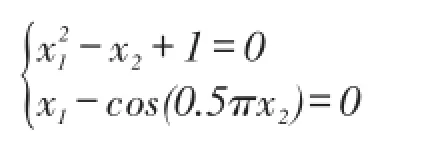
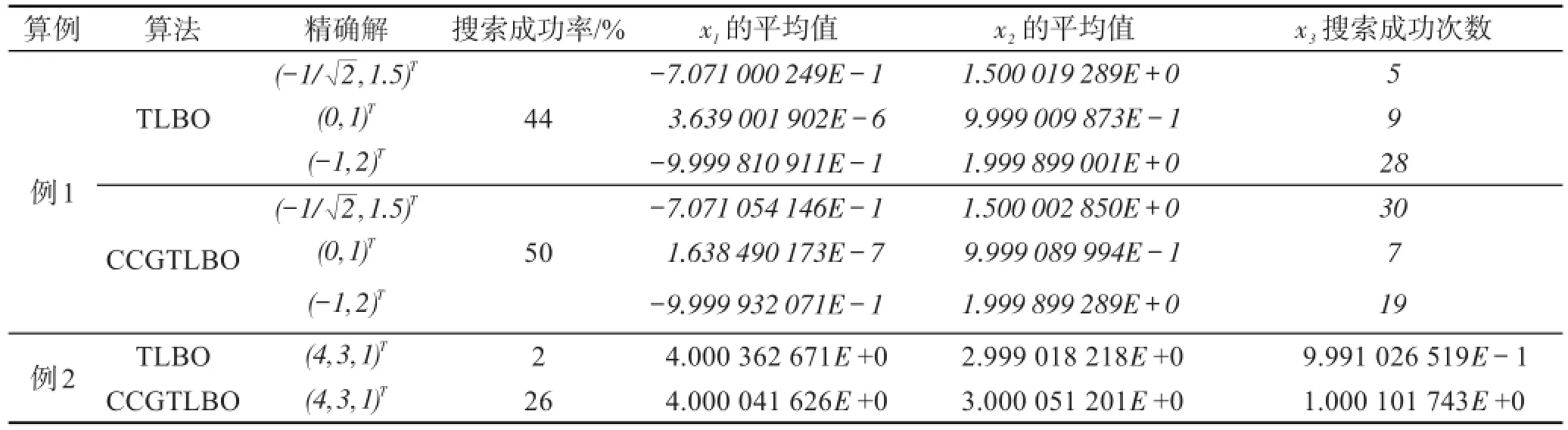
Table 3　Results comparison of TLBO and CCGTLBO for solving nonlinear equations表3　TLBO与CCGTLBO求解非线性方程组的结果对比

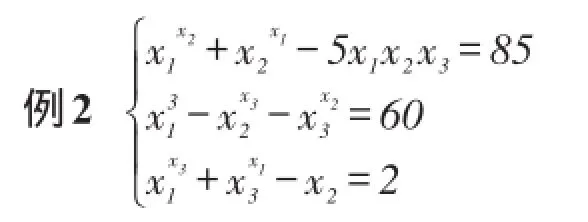
该方程理论精确解是x*=(4,3,1)T，求解范围是x∈[0,10]。

通过表3所列数据可以看出，在两个示例上，CCGTLBO算法的解精度和搜索成功率均要优于标准TLBO，证明改进后算法的稳定性和全局收敛能力较标准教与学优化算法有了很大的提高。

5　结束语

本文针对教与学优化算法在求解高维问题时，容易出现早熟，解精度较低的弱点，通过引入4点改进机制提升算法的性能。首先，通过利用Chebyshev混沌优化机制实现种群初始化，提高原始种群对于解空间的覆盖。为了加强算法的局部搜索能力，嵌入精英个体的共轭梯度搜索机制。通过引入一个动态自适应学习因子，使种群的多样性得以保持。针对多次迭代后仍然难以提高的劣质个体，采用反向学习和高斯学习对其进行二次强化学习，协助它们跳出局部极值的约束。最后一系列的实验表明，改进算法在收敛精度、成功率方面均优于标准TLBO算法，适合于求解高维的函数优化问题。

教与学优化算法出现时间较短，但已经引起国内外专家学者的注意。今后将会针对其收敛性进行理论方面的论证，以及研究如何借鉴传统的演化算法优点，实现优势互补，拓展其应用领域。

References:

[1]Rao RV,SavsaniVJ,Vakharia D P.Teaching-learning-based optimization:an optimization method for continuous nonlinear large scale problems[J].Information Sciences,2012, 183:1-15.

[2]Črepinšek M,Liu S H,Mernik L.Anote on teaching-learningbased optimization algorithm[J].Information Sciences,2012, 212:79-93.

[3]Tuo Shouheng.A modified teaching-learning-based optimization algorithm and application in neural networks[J]. CAAI Transactions on Intelligent Systems,2013,8(4):327-332.

[4]Rao R V,Patel V.Multi-objective optimization of heat exchangers using a modified teaching-learning-based optimization algorithm[J].Applied Mathematical Modeling,2013, 37(3):1147-1162．

[5]Toğan V.Design of planar steel frames using teaching-learning based optimization[J].Engineering Structures,2012,34(1): 225-232.

[6]Krishnanand K R,Panigrahi B K,Rout P K,et al.Application of multi-objective teaching-learning-based algorithm to an economic load dispatch problem with incommon-surable objectives[C]//LNCS 7076:Proceedings of the 2nd International Conference on Swarm,Evolutionary,and Memetic Computing,Visakhapatnam,India,Dec 19-21,2011.Berlin, Heidelberg:Springer,2011:697-705．

[7]Rao R V,Savsani V J,Vakharia D P.Teaching-learning-based optimization:a novel method for constrained mechanical design optimization problems[J].Computer-Aided Design, 2011,43(3):303-315．

[8]Yu Kunjie,Wang Xin,Wang Zhenlei.Study and application of improved teaching-learning-based optimization algorithm[J]. Chemical Industry and Engineering Progress,2013,33(4): 850-854.

[9]Rao R V,Patel V.An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems[J].International Journal of Industrial Engineering Computations,2012,3(4):535-560.

[10]Gao Liqun,Ouyang Haibin,Kong Xiangyong,et al.Teachinglearning based optimization algorithm with crossover operation[J],Journal of Northeastern University:Natural Science,2014,35(3):323-327.

[11]Rajasekhar A,Rani R,Ramya K,et al.Elitist teaching-learning opposition based algorithm for global optimization[C]//Proceedings of the 2012 IEEE International Conference on Systems,Man,and Cybernetics,Seoul,Korea,Oct 14-17,2012. Piscataway,USA:IEEE,2012:1124-1129.

[12]Yu Kunjie,Wang Xin,Wang Zhenlei.Elitist teaching learningbased optimization algorithm based on feedback[J].Acta Automatica Sinica,2014,40(9):1976-1983.

[13]Yu Shuhao,Su Shoubao.Research and application of chaotic glowworm swarm optimization algorithm[J].Journal of Frontiers of Computer Science and Technology,2014,8(3): 352-358.

[14]Wu Xiaoping,Wang Tongtong.A 3-D finite-element resitivity forward modeling using conjugate gradient algoritm[J]. Chinese Journal of Geophysics,2003,46(3):428-432.

[15]Tizhoosh H R.Opposition-based learning:a new scheme for machine intelligence[C]//Proceedings of the 2005 IEEE International Conference on Computational Intelligence for Modelling,Control and Automation,Vienna,Austria,Nov 28-30,2005.Piscataway,USA:IEEE,2005:695-701.

[16]Zhan Zhihui,Zhang Jun,Li Yun,et al.Adaptive particle swarm optimization[J].IEEE Transaction on Systems,Man, and Cybernetics,2009,39(6):1362-1381.

[17]Rao R V,Patel V.An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems[J].Scientia Iranica,2013,20(3):710-720.

[18]Wang Peichong.Swarm intelligence algorithms and their apllications[M].Beijing:Publishing House of Electronics Industry,2015.

附中文参考文献：

[3]拓守恒.一种优化神经网络的教与学优化算法[J].智能系统学报,2013,8(4):327-332.

[8]于坤杰,王昕,王振雷.改进的教学优化算法及其应用[J].化工进展,2013,33(4):850-854.

[10]高立群,欧阳海滨,孔祥勇,等.带有交叉操作的教-学优化算法[J].东北大学学报:自然科学版,2014,35(3):323-327.

[12]于坤杰,王昕,王振雷.基于反馈的精英教学优化算法[J].自动化学报,2014,40(9):1976-1983.

[13]郁书好,苏守宝.混沌萤火虫优化算法的研究及应用[J].计算机科学与探索,2014,8(3):352-358.

[14]吴小平,汪彤彤.利用共轭梯度算法的电阻率三维有限元正演[J].地球物理学报,2003,46(3):428-432.

[18]王培崇.群体智能算法及其应用[M].北京:电子工业出版社,2015.

WANG Peichong was born in 1972.He received the Ph.D.degree in computer science and technology from China University of Mining and Technology(Beijing)in 2010.Now he is an associate professor at School of Information Engineering,Hebei Dizhi University.His research interests include evolutionary computation,machine learning and pattern recognize,etc.He has published more than 30 papers in domestic and international journals and conferences.

王培崇（1972—），男，河北辛集人，2010年于中国矿业大学（北京）计算机应用技术专业获得博士学位，现为河北地质大学信息工程学院副教授，主要研究领域为进化计算，机器学习，模式识别等。发表学术论文30余篇。

PENG Feifei was born in 1986.She received the Ph.D.degree in computer science and technology from China University of Mining and Technology(Beijing)in 2012.Now she is a lecturer at Information Center of Library,Beijing University of Posts and Telecommunications.Her research interests include evolutionary computation and machine learning,etc.She has published more than 20 papers in domestic and international journals and conferences.

彭菲菲（1986—），女，山东青岛人，2012年于中国矿业大学（北京）计算机应用技术专业获得博士学位，现为北京邮电大学图书馆信息中心讲师，主要研究领域为进化计算，机器学习等。发表学术论文20余篇。

QIAN Xu was born in 1962.He received the Ph.D.degree in control science and engineering from China University of Mining and Technology in 1996.Now he is a professor and Ph.D.supervisor at School of Mechanical Electronic and Information Engineering,China University of Mining and Technology(Beijing).His research interests include software engineering and machine learning,etc.He has published more than 100 papers in domestic and international journals and conferences.

钱旭（1962—），男，江苏南京人，1996年于中国矿业大学控制科学与工程专业获得博士学位，现为中国矿业大学（北京）机电与信息工程学院教授、博士生导师，主要研究领域为软件工程，机器学习等。发表学术论文100余篇。

+Corresponding author:E-mail:wpeichong@126.com

文献标志码：A

中图分类号：TP18

doi:10.3778/j.issn.1673-9418.1508071

Improved Teaching-Learning Based OptimizationAlgorithm with Conjugate Gradient Methods and Second Study*

WANG Peichong1,2+,PENG Feifei3,QIAN Xu2
1.School of Information Engineering,Hebei Dizhi University,Shijiazhuang 050031,China
2.School of Mechanical Electronic and Information Engineering,China University of Mining and Technology,Beijing 100083,China
3.Library,Beijing University of Posts and Telecommunications,Beijing 100083,China

Abstract:Teaching-learning based optimization(TLBO)algorithm can solve the complex optimization problems by simulating teaching and learning,and has been applied in many fields.To overcome the weakness of premature,low precision of solution,this paper proposes an improved hybrid chaotic and conjugate gradient method TLBO.This improved algorithm initializes its population by Chebyshev mapping to improve bestrow rate of solution space.To keep the diversity of population,this paper introduces a dynamic learning coefficient to make that students can mainly learn from teacher in early,and improves gradually the ability of affecting itself evolvement of studentƳs knowledge.In its iteration,teacher individual executes conjugate gradient methods after“teaching”and“learning”.If the states of those student indivduals which are worst can not be changed,second study based on OBL(opposition-based learning)

Key words:teaching-learning based optimization;Chebyshev mapping;dynamic self-adaptive learning;conjugate gradient method;second study

*The Social Science Foundation of Hebei Province under Grant No.HB16TQ001(河北省社会科学基金). Received 2015-08,Accepted 2015-11.