具有第二下降点6错线性复杂度的2n周期序列*
2016-05-28王喜凤周建钦安徽工业大学计算机科学与技术学院安徽马鞍山243002
王喜凤,张 伟,周建钦安徽工业大学 计算机科学与技术学院,安徽 马鞍山 243002
具有第二下降点6错线性复杂度的2n周期序列*
王喜凤,张伟+,周建钦
安徽工业大学 计算机科学与技术学院,安徽 马鞍山 243002
WANG Xifeng,ZHANG Wei,ZHOU Jianqin.2n-periodic binary sequences with 6-error linear complexity as the second descent point.Journal of Frontiers of Computer Science and Technology,2016,10(6):838-846.
摘要:线性复杂度和k错线性复杂度是衡量流密码强度的重要指标,通常这两个指标越大就越能抗击明文攻击。为了更进一步地研究密钥流序列,利用构造方法和方体理论分析了具有第二下降点6错线性复杂度的2n周期序列,得到了所有可能6错线性复杂度的取值形式。分析并推导了具有2错线性复杂度为第一次下降点且6错线性复杂度为第二次下降点的2n周期序列的计数公式。使用这种方法也可以推导出其他具有第二次下降点或者第三次下降点的k错线性复杂度序列的相关性质。
关键词:周期序列;线性复杂度;k错线性复杂度;方体理论
ISSN 1673-9418CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology
1673-9418/2016/10(06)-0838-09
E-mail:fcst@vip.163.com
http://www.ceaj.org
Tel:+86-10-89056056
1 引言
将能够产生序列s的最短的线性反馈移位寄存器(linear feedback shifting register,LFSR)的级数称为序列s的线性复杂度,记为L(s)。线性复杂度L(s)及其稳定性在衡量流密码的强度时具有重要作用。通常线性复杂度足够大就越能抗击明文攻击,但是有些序列的线性复杂度不稳定,改变一个周期内的若干个元素就能使序列的线性复杂度产生极大的变化。为了更好地衡量流密码的强度,我国学者Ding等人[1]率先提出了重量复杂度和球体复杂度。随后,国外学者Stamp等人[2]又提出了k错线性复杂度的概念。k错线性复杂度Lk(s)反映了序列线性复杂度的稳定性[3-6]。
为了研究一个序列s的k错线性复杂度在哪些点下降。Etzion等人[7]最早提出了关键线性复杂度分布(critical error linear complexity spectrum,CELCS)的概念,CELCS由一系列关键错误点(k,Lk(s))构成,满足k 本文以Games-Chan算法[14]为基础,利用方体理论,研究了具有2错线性复杂度为第一次下降点且6错线性复杂度为第二次下降点的周期序列的性质;分析了两次线性复杂度下降的关系,给出了6错线性复杂度的取值形式,并且给出了满足这种情况的序列的计数公式。 首先介绍几个重要的引理和定义,然后介绍基于Games-Chan算法的方体理论,以及如何用筛选法确定关键错误线性复杂度分布。 设有限域GF(2)上的两个向量分别为:α=(x1,x2, …,xn)和 β=(y1,y2,…,yn),则定义 α+β=(x1+y1,x2+ y2,…,xn+yn),本文讨论的序列都是在有限域GF(2)中的序列,其中“+”和“⊕”运算都为模2运算。 2.1相关定义和引理 文献[15-20]具体介绍了方体理论及相关性质,这里只给出下文将要用到的相关定义。 引理1[15]设周期N=2N的二元序列s,其线性复杂度L(s)=2n,当且仅当该序列的一个周期中汉明重量为奇数。 引理2[16]设周期N=2N的二元序列s1和s2,若L(s1)=L(s2),则L(s1+s2) 则映射具有以下性质: 注:WH(s(n))意为序列s(n)的汉明重量。 引理4[18]设满足线性复杂度为L,0≤L≤2n的二元周期序列的个数N(L)为: 定义1[19]设存在正整数x和y,若二进制周期序列s中两个元素位置差为(2x+1)×2y,则称这两个元素的距离为2y。 定义2[19]设周期为2n的二元序列s中有2m个非零元素,其中0≤i1 引理5[20]设s为周期为2n的二元序列且为m方体,若m方体的边长分别为2i1,2i2,…,2im且0≤i1< i2<… 2.2筛选法 设c为二元序列s的k错线性复杂度,e是汉明重量为k的误差序列,那么设s=t+e,L(t)=c。若有如下框架:设T={t|L(t)=c},E={e|WH(e)=k},TE={t+e| t∈T,e∈E},其中e是WH(e)=k的序列,t是线性复杂度为c的序列。使用筛选法,目的是从TE中筛选出Lk(t+e)=c的序列t+e。 对于给定线性复杂度c,求满足Lk(t+e)=c的序列t+e,需要排除一些不满足条件的序列。此时不满足条件的序列有两类:一类是 t+u∈TE,但Lk(t+u) 对于Lk(t+u) 对于 Lk(x+u)=Lk(y+v)=c,但 x+u=y+v的情况。由x+u=y+v可知x+y=u+v;又因为L(x)=L(y)= c,根据引理2知L(x+y) 首先使用方体理论来分析k错线性复杂度的第一次和第二次下降的关系,并给出所有可能的取值形式。然后给定序列线性复杂度的第一次下降点和第二次下降点,求出满足条件的所有可能序列的计数。 定理1 设周期二元序列 s(n),若 L6(s(n)) 证明 利用反证法进行证明,假设i0∉{i,j,k}。 存在2n周期二元序列s(n),序列s(n)改变两个元素得到序列u={1111 0000 1111 0000}。此时序列u的线性复杂度L(u)=L2(s(n))=2n-(20+21+23),可知i=0, j=1,k=3。若存在i0∉{i,j,k},那么i0=2或i0=4。 当i0=2时,因为序列 s(n)的线性复杂度 L(s(n))= 2n-2i0,所以存在序列v={1000 1000 0000 0000}使得u+v={0111 1000 1111 0000},并且序列s(n)的线性复杂度L(s(n))=L(u+v)=2n-22。此时序列s(n)改变两个元素后线性复杂度出现第一次下降且L(u)=L2(s(n))= 2n-(20+21+23)=5,根据序列性质知第二次下降点Lk(s(n)) 式中“…”代表L(u+v+t),并且 可以看出,只有当k=8时,即WH(t)=8时,序列线性复杂度才出现第二次下降,此时与条件矛盾。 当i0=4时,序列s(n)的线性复杂度L(s(n))=2n-24,因为n=i0=4,根据方体理论的性质,当i0=4时,两个非零元素的距离为24=16。因为序列的长度为16,所以两个非零元素的最长距离为8。从而不存在i0=4这种情况。 综上所述,只有当k=8时,即WH(t)=8时,序列线性复杂度才出现第二次下降,此时与条件矛盾。因此假设不成立,则i0∈{i,j,k}。 定理2已知周期为2n的二元序列 s(n),且L(s(n))<2n,则: (1)L6(s(n)) (2)L6(s(n)) 证明(1)①必要性:由Kurosawa[4]知,一个周期为s(n)的二元序列s,线性复杂度为: 存在kmin=2m使得序列s的k错线性复杂度小于L(s(n))。因c1是1方体,c2是3方体,则L5(s(n))=L4(s(n))=L2(s(n))。 当c1、c2的非零元素均不重合时,去掉c1的两个非零元素线性复杂度第一次下降。在c1上增加6个1将变成一个3方体,和c2形成一个4方体,此时线性复杂度第二次下降,即L6(s(n)) 当c1的非零元素和c2的一个非零元素重合时,将c2中重合的位置加上非零元素,将c1中没有重合的非零元素去掉,即将序列s(n)中的c1去掉,此时L2(s(n)) 当c1的非零元素和c2非零元素都相交时,将c2中两个重合的位置加上非零元素,此时3方体c2决定着此时序列的线性复杂度,故L2(s(n)) ②充分性:假设c1、c2、c3均为1方体,其中3个方体的非零元素互不重合,且在c1、c2、c3中添加两个非零元素时,不能构成一个方体。首先去掉c1时,线性复杂度下降;再同时去掉c1和c2时,线性复杂度再次下降,即L4(s(n)) 假设c1为1方体,c2为2方体,c1和c2的非零元素可以不重合,可以有一个重合,也可以有两个重合。当 c1和 c2的非零元素可以不重合时,如{1111 1100 0000 0000},此时等价于c1为1方体,c2为3方体,且c1和c2非零元素有两个重合。当c1和c2非零元素有两个重合时,分别去掉c1和c2非零元素,则线性复杂度下降,即L4(s(n)) 假设c1为1方体,c2为4方体,c1和c2的非零元素可以不相交,可以有一个重合,可以有两个重合。因为c2为4方体,所以第二次下降至少需要改变14个非零元素线性复杂度才下降,即L14(s(n)) 综上所述,只有当c1为1方体,c2为3方体时满足上述情况。 (2)由(1)易知L6(s(n)) 定理3设序列s(n)为周期为2n的二元序列,如果L6(s(n)) 证明 T={t|L(t)=L},E={e|L(e)=6},TE={t+e|t∈T,e∈E},其中L(t)=L6(s(n)),WH(e)=6,L2(s(n))=2n-(2i+ 2j+2k),使用筛选法,从TE中筛选出L6(t+e)=L的序列t+e。关于L6(t+e) 当i0=i时{i1,i2,i3}不包含{i,j},{i,k}。假设n=5,i01,i=0,j=1,k=3。 则存在序列 则存在序列 同理可证:当i0=j时{i1,i2,i3}不包含{i,j},{j,k};i0= k时{i1,i2,i3}不包含{i,k},{j,k}。 同理,v={0101 0000 1100 0000 0101 0000 0000 0000}时,可证i1≠i;v={0111 0000 0100 0000 1000 0000 1000 0000}时,可证i1≠k;v={0111 1000 0100 1000 0000 0000 0000 0000}时,可证i2≠k。 定理4设s(n)是2n周期的二元序列,线性复杂度为2n。 (1)L2(s(n))=2n-(2i+2j+2k),L6(s(n)) ①当i0=i时 (2)若L6(s(n))=0,则满足上述条件的2n周期的二元序列s(n)的个数有如下3种情况: ①当i0=i时 ②当i0=j时 ③当i0=k时 证明 定理4的证明过程中,首先利用构造法分析出L6(s(n))=0的情况的具体个数,然后利用筛选法,筛选出符合条件的L6(s(n))≠0的序列,具体过程如下: (1)由引理知,线性复杂度L(t)=L的2n周期二元序列t的个数是2L-1。 (2)下面推导当i0=i时序列e的个数,其中WH(e)=6且L2(e)=2n-(2i+2j+2k)。 步骤1设s(i)是周期为2i的二元序列,线性复杂度为2i且WH(s(i))=1,则s(i)的个数为2i。 步骤2设s(i+1)是周期为2i+1的二元序列,线性复杂度为2i+1-2i=2i且WH(s(i+1))=2,则s(i+1)的个数为2i。 步骤3当 j>i时,设s(j)是周期为2j的二元序列,线性复杂度为2j-2i且WH(s(j))=2,则s(j)的个数为2i×(22)j-i-1。 步骤4设s(j+1)是周期为2j+1的二元序列,线性复杂度为2j+1-(2i+2j)且WH(s(j+1))=4,则s(j+1)的个数为2i×(22)j-i-1。 步骤5当k>j时,设s(k)是周期为2k的二元序列,线性复杂度为2k-(2i+2j)且WH(s(k))=4,则s(k)的个数为2i×(22)j-i-1×(24)k-j-1。 步骤6已知序列s(k)中已经有4个非零元素分别是p1、p2、p3、p4,在序列s(k+1)上加两个非零元素p5、p6,构成周期为2k+1的二元序列s(k+1)。因p5、p6的距离为2k-2i,使p5、p6和 p1、p2、p3、p4任意元素的距离为2k,则一共有4种方案,若p1、p2和p5、p6的距离为2k,则剩下的两个元素p3、p4有22种选择,则s(k+1)序列的个数为2i×(22)j-i-1×(24)k-j-1×4×22。 步骤7当s>k时,设s(n)是周期为2n的二元序列,线性复杂度为2n-(2i+2j+2k)且WH(e)=6,则序列s(n)的个数是2i×(22)j-i-1×(24)k-j-1×4×22×(26)n-k-1。 由上可知,当i0=i时,满足e∈E,L(e)=2n-2i0,L2(e)=2n-(2i+2j+2k),i0=i的序列e的个数为: 同理可证,当i0=j时,满足e∈E,L(e)=2n-2i0,的序列e的个数: 当 i0=k时,满足 e∈E,L(e)=2n-2i0,L2(e)= 2n-(2i+2j+2k),i0=k的序列e的个数为: 由上可知,当L6(s(n))=0时,满足条件的周期为2n的二元周期序列s(n)在i0=i,i0=j,i0=k这3种情况下的个数。 (3)因s+u,t+v∈SE,L6(s+u)=L6(t+v)=L,其中s≠t,u≠v,但s+u=t+v,检查是否存在序列v,WH(u)=WH(v)=6,使L(u+v)=L(s+t) ①序列v的个数与参数α、β相关,其中β<α 下面讨论i0=i时重复序列的具体个数:任给u∈E,存在1个序列v,使L(u+v)=2n-(2i+2α+2k)< L,此时 λi=1;存在2个序列 v,使 L(u+v)=2n-(2α+2k) 下面举例证明,假设n=5,i0=1,i=1,j=2,k=4,α=3 则存在序列 使L(u(5)+v(5)1)=2n-(2i+2α+2k)=25-(21+23+24)<25-(20+23+24)=L,则存在 同理可得,i0=j时,任给u∈E,存在1个序列v,使L(u+v)=2n-(2j+2α+2k) 下面分别举例说明i0=i,i0=j,i0=k的情况: 当i0=i时,假设n=5,i0=1,i=1,j=2,k=3,已知序列 则存在序列 同理可证: 综上所述,定理4得证。 下面举例来进一步验证定理4,并且其正确性已用计算机程序进行了验证。 例1n=5,i0=0,i=0,j=1,k=3,i1=1,i2=2, 例2n=5,i0=3,i=0,j=1,k=3,i1=0,i2=2, 本文在Games-Chan算法和筛选法的基础上,用方体理论和筛选法研究周期为2n的二进制序列s(n)的6错线性复杂度的相关性质,其中序列s(n)的2错线性复杂度是第一次下降,序列s(n)的6错线性复杂度是第二次下降。给出了6错线性复杂度的所有可能的取值形式,并且推导出了完整的计数公式。对于其他具有第二次下降点k错线性复杂度序列,也能使用此种方法。同理可研究具有三次下降点k错线性复杂度的序列。 References: [1]Ding Cunsheng,Xiao Guozhen,Shan Weijuan.The stability theory of stream ciphers[M]//Lecture Notes in Computer Science 561.Berlin,Heidelberg:Springer,1991:85-88. [2]Stamp M,Martin C.F.An algorithm for the k-error linear.co mplexity of binary sequence with period2n[J].IEEE Transactions on Information Theory,1993,39(4):1398-1401. [3]Kurosawa K,Sato F,Sakata T,et al.A relationship between linear complexity and k-error linear complexity[J].IEEE Transactions on Information Theory,2000,46(2):694-698. [4]Tan Lin,Qi Wenfeng.Linear complexity and k-error linear complexity for2mpn-periodic binary sequences[J].Journal on Communication,2008,29(7):44-49. [5]Zhou Jianqin.On the 3-error linear complexity of2n-periodic binary sequences with linear complexity2n[J].Acta MathematicaeApplicatae Sinica,2013,36(3):399-413. [6]Fu Fangwei,Niederreiter H,Su Ming.The characterization of2n-periodic binary sequences with fixed 1-error linear complexity[C]//LNCS 4086:Proceedings of the 4th International Conference on Sequences and Their Applications,Beijing,China,Sep 24-28,2006.Berlin,Heidelberg:Springer, 2006:88-103. [7]Etzion T,Kalouptsidis N,Kolokotronis N,et al.Propertics of the error linear complexity spectrum[J].IEEE Transactions on Information Theory,2009,55(10):4681-4686. [8]Pi Fei,Qi Wenfeng.The 4-error linear complexity of binary periodic sequences[J].Acta Electronica Sinica,2011,39 (12):2914-2920. [9]Niu Zhihua,Guo Danfeng.New algorithm for computing minerror linear complexity ofpn-periodic binary sequences[J]. Journal of ComputerApplications,2013,33(1):12-14. [10]Wang Hongcui,Zhou Jianqin.Original sequence counting functions ofpnperiodic sequence 3-error linear complexity[J]. Journal of Hangzhou Dianzi University,2013(6):37-40. [11]Zhou Jianqin.On the 2-error linear complexity of2n-periodic balanced binary sequences[J].Journal of Suzhou University of Science and Technology:Natural Science Edition,2013, 30(4):1-7. [12]Zhou Jianqin,Liu Wanquan,Wang Xifeng.Structure analysis on the k-error linear complexity for2n-periodic binary sequence[J/OL].arXiv:1312.6927v2(2014-08-09)[2015-03-11].http://arxiv.org/pdf/1312.6927.pdf. [13]Games R A,Chan A H.A fast algorithm for determining the complexity of a binary sequence with period2n[J].IEEE Transactions on Information Theory,1983,29(1):144-146. [14]Zhou Jianqin,Liu Wanquan.On the k-error linear complexity for2n-periodic binary sequences via cube theory[J].arXiv: 1309.1829v1(2013-09-07)[2015-03-11].http://arxiv.org/ pdf/1309.1829.pdf. [15]Zhou Jianqin,Liu Wanquan.The k-error linear complexity distribution for2n-periodic binary sequences[J].Designs, Codes and Cryptography,2014,73(1):55-75. [16]Meidl W.On the stablity of2n-periodic binary sequences[J]. IEEE Transactions on Information Theory,2005,51(3): 1151-1155. [17]Rueppel R A.Analysis and design of stream ciphers[M]. Berlin:Springer-Verlag,1986. [18]Zhou Jianqin,Dai Xiaoping.On the stable k-error linear complexity of periodic sequences[J].Journal on Communication,2011,32(11A):213-220. [19]Zhu Fengxiang,Qi Wenfeng The 2-error linear complexity of 2n-periodic binary sequences with linear complexity2n-1[J]. Journal of Electronics,2007,24(3):390-395. [20]Zhou Jianqin,Ouyang Kongli.On k-error linear complexity ofpn-periodic sequences overGF(q)[J].Journal of Jishou University:Natural Science Edition,2013,34(6):41-46. 附中文参考文献: [4]谭林,戚文峰.2mpn周期二元序列的线性复杂度和k错线性复杂度[J].通信学报,2008,29(7):44-49. [5]周建钦.具有2n线性复杂度的2n周期二元序列的3错线性复杂度[J].应用数学学报,2013,36(3):399-413. [8]皮飞,戚文峰.二元周期序列的4-错线性复杂度[J].电子学报,2011,39(12):2914-2920. [9]牛志华,郭丹峰.计算pn周期二元序列的最小错线性复杂度新算法[J].计算机应用,2013,33(1):12-14. [10]王洪翠,周建钦.pn周期序列3错线性复杂度原序列计数公式[J].杭州电子科技大学学报,2013(6):37-40. [11]周建钦.2n周期平衡二元序列的2错线性复杂度[J].苏州科技学院学报:自然科学版,2013,30(4):1-7. [18]周建钦,戴小平.具有稳定k错线性复杂度的周期序列[J].通信学报,2011,32(11A):213-220. [20]周建钦,欧阳孔礼.GF(q)上pn-周期序列的k错线性复杂度[J].吉首大学学报:自然科学版,2013,34(6):41-46. WANG Xifeng was born in 1980.She is a lecturer at Anhui University of Technology.Her research interests include communication,information security and cryptography,etc. 王喜凤(1980—),女,山东成武人,硕士,安徽工业大学讲师,主要研究领域为通信,信息安全,密码学等。 ZHANG Wei was born in 1989.He is an M.S.candidate at Anhui University of Technology.His research interests include information security and cryptography,etc. 张伟(1989—),男,安徽合肥人,安徽工业大学硕士研究生,主要研究领域为信息安全,密码学等。 ZHOU Jianqin was born in 1963.He received the M.S.degree from Fudan University in 1989.Now he is a professor at Anhui University of Technology.His research interests include communication,information security and cryptography,etc. 周建钦(1963—),男,山东巨野人,1989年于复旦大学获得硕士学位,现为安徽工业大学教授,主要研究领域为通信,信息安全,密码学等。 *The National Natural Science Foundation of China under Grant No.61300059(国家自然科学基金);the Natural Science Foundation of Anhui Province under Grant No.1208085MF106(安徽省自然科学基金);the Natural Science Research Project of Anhui Colleges under Grant No.KJ2013Z025(安徽省教育厅自然科学研究项目);the Youth Foundation Project of Anhui University of Technology under Grant No.QZ201412(安徽工业大学青年基金项目). Received 2015-04,Accepted 2015-09. CNKI网络优先出版:2015-10-14,http://www.cnki.net/kcms/detail/11.5602.TP.20151014.1722.002.html +Corresponding author:E-mail:waynezh89@163.com 文献标志码:A 中图分类号:TN918.1 doi:10.3778/j.issn.1673-9418.1504035 2n-Periodic Binary Sequences with 6-Error Linear Complexity as the Second Descent Pointƽ WANG Xifeng,ZHANG Wei+,ZHOU Jianqin Abstract:The linear complexity and the k-error linear complexity are important indicators to measure the strength of stream ciphers,and the higher of those two indicators could resistance the plaintext attack than others,generally. In order to research the sequence of stream cipher,this paper uses a structural approach and cube theory in investigating the 2n-periodic binary sequences with 6-error linear complexity as the second descent point,and gets all the possible value forms of 6-error linear complexity.This paper analyzes and derives the complete counting functions of 2n-periodic binary sequences with the given first descent point 2-error linear complexity and second descent point 6-error linear complexity.With the method proposed in this paper,other second or third descent point of the k-error linear complexity for 2n-periodic binary sequences can be obtained. Key words:periodic sequence;linear complexity;k-error linear complexity;cube theory2 预备知识与引理
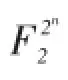



3 具有第二下降点6错线性复杂度的周期序列计数














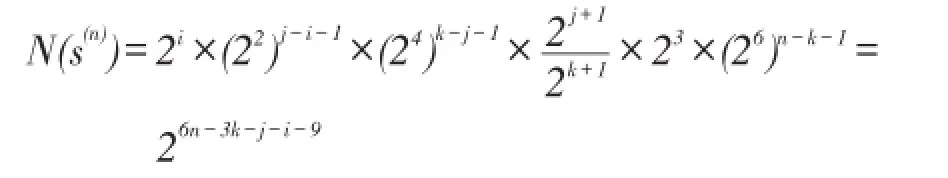














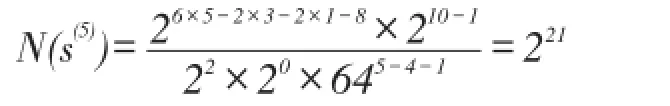



4 结论



Computer Science and Technology School,Anhui University of Technology,Ma’anshan,Anhui 243002,China
