异方差加噪下的差分隐私直方图发布算法*

康　健，吴英杰，黄泗勇，陈　鸿，孙　岚福州大学 数学与计算机科学学院，福州 350116



异方差加噪下的差分隐私直方图发布算法*

康健，吴英杰+，黄泗勇，陈鸿，孙岚
福州大学 数学与计算机科学学院，福州 350116

KANG Jian,WU Yingjie,HUANG Siyong,et al.Algorithm for differential privacy histogram publication with non-uniform private budget.Journal of Frontiers of Computer Science and Technology,2016,10(6):786-798.

摘要：现有基于区间树结构的差分隐私直方图发布方法大多采用同方差加噪方式，对其进一步研究发现，采用异方差加噪策略可以进一步提升发布直方图的区间计数查询精度，然而当前基于异方差加噪的差分隐私直方图发布方法对区间树结构却有严格的要求，导致灵活性与实用性较低。为此，提出了一种异方差加噪下面向任意区间树结构的差分隐私直方图发布算法LUE-DPTree（inear unbiased estimator for differential private tree）。首先根据区间计数查询的分布，计算区间树中节点的覆盖概率，并据此分配隐私预算，实现异方差加噪；接着经分析指出该异方差加噪策略适用于任意区间树结构，且从理论上证明了在任意区间树结构下进行异方差加噪后，仍可在一致性约束下利用最优线性无偏估计进一步降低区间计数查询的误差。针对算法的区间计数查询精度及执行效率，与同类算法进行了比较分析。实验结果表明，LUE-DPTree算法是有效可行的。

关键词：隐私保护；差分隐私；直方图发布；异方差加噪；区间树

ISSN 1673-9418CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(06)-0786-13

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

1　引言

随着信息技术的发展，大量数据的收集与发布在促进科学技术进步的同时，也带来了隐私信息泄露的问题。因此，数据发布隐私保护成为现今一项热门的研究课题。

近年来，在数据发布隐私保护领域，研究人员开展了一系列的研究，主要可分为数据加密、限制发布和数据扰乱等方面[1-3]，包括k-anonymity[4]、l-diversity[5]等保护方法。其中，Dwork[6]提出了差分隐私保护模型。该模型采用了严格的量化评估标准，能够实现有效的隐私保护，并保证较高的数据可用性。此后，研究人员在差分隐私保护的各个领域展开了大量研究，其中包括差分隐私直方图发布方法的研究[7-15]，主要包含层次树变换、聚类变换和傅里叶变换等[3]。本文主要针对层次树变换中基于区间树的差分隐私直方图发布方法进行讨论。

现有基于区间树的差分隐私直方图发布方法大多采用同方差的加噪方式。Hay等人[8]建立了差分隐私区间树，并进行了同方差加噪与一致性调节。Xu等人[9]提出了StructureFirst，优化直方图划分策略，并在划分区间后的构造区间树中进行了同方差加噪。采用同方差加噪方式的发布方法有效提升了发布数据的可用性和算法效率。而实际上通过研究可以发现，若采用异方差加噪方式，可进一步提高发布精度。文献[10]提出了通过迭代方式在区间树进行层次间隐私预算分配的方法，有效降低了查询误差，但其在相同层次的节点中仍使用相同的隐私预算，因此仍具有进一步优化的空间。文献[11]提出了DP-tree（differential private tree），通过异方差加噪，能够对多维数据进行发布并提高查询精度，但该方法采用了完全K叉树结构，限制了树结构调节的灵活性。

针对以上问题，本文提出了一种异方差加噪下，面向任意区间树结构的差分隐私直方图发布算法，以期进一步降低区间计数查询误差，提高发布数据的可用性。

2　基础知识与问题

在现有差分隐私直方图发布方法的研究中，主要通过重构直方图结构来回答区间计数查询，代表方法为基于差分隐私区间树的发布方法。该方法利用区间树结构重构原始直方图，可有效提高发布数据的精确度和算法运行效率。

定义1（差分隐私区间树[8]）对于给定计数直方图H={C1,C2,…,Cn}，对H建立的差分隐私区间树T满足以下特性：

（1）非叶节点的儿子节点数大于等于2。

（2）每个节点x对应于H中的一个区间范围，表示为[L(x),R(x)]，根节点所代表的区间为[1,n]。

定义2（同/异方差加噪方式[8,11]）给定区间树T，通过噪声机制[8]使每个节点x满足εx-差分隐私。若对任意节点x、y，均有εx=εy，则称作同方差加噪方式；若存在节点x、y，使得εx≠εy，则称作异方差加噪方式。

如图1，当ε=1.0时，在图1（a）的同方差加噪方式下，区间树的每个节点的隐私预算εx均为0.5。而在图1（b）的异方差加噪方式中，节点1隐私预算为0.33，节点2、3、4的隐私预算均为0.67。由于通常情况下，区间树中的各个节点被查询区间覆盖的频率并不完全相同。例如在查询区间随机分布的情况下，节点2、3、4具有高于节点1的覆盖概率（计算过程将在下文给出），因此在图1（b）中能够对多数高频覆盖节点添加更少的噪声，对少数低频覆盖节点添加更多噪声，从而降低整体区间计数查询误差。

Fig.1　Uniform/non-uniform private budget distribution图1　同/异方差加噪下的隐私预算分配

定义3（查询一致性约束[8]）在发布后的差分隐私区间树T中，任意节点x的计数值应与其儿子节点的计数值总和相等，称为查询一致性约束：

其中，hˉ代表最终发布后节点的计数值；Son(x)为节点x的儿子节点集合。

现有基于区间树结构的差分隐私直方图发布方法大多采用同方差的加噪方式，少数采用异方差加噪的差分隐私直方图发布方法对树结构有着严格的要求。为此，本文的研究问题及目标是：对于给定的原始直方图H，建立与其对应的差分隐私区间树T，并通过异方差方式进行加噪；接着说明该加噪方式适用于任意区间树结构，并利用查询一致性约束条件进一步优化区间计数查询精度；最后提出异方差加噪下面向任意区间树结构的差分隐私直方图发布算法LUE-DPTree，同时保证算法满足ε-差分隐私。

3　异方差加噪下面向任意区间树结构的差分隐私直方图发布算法

为实现异方差加噪，首先需要解决区间树中节点的覆盖概率计算问题，并据此进行隐私预算分配。

3.1节点覆盖概率计算

当对区间树进行区间计数查询时，其计数值为查询区间[QL,QR]所覆盖的多个节点计数值之和[8]。所覆盖的节点互不相交，且并集等于查询区间，因此被覆盖节点x需满足QL≤L(x)≤R(x)≤QR。同时，对任意一次查询，若其父节点fx能被查询区间覆盖，节点x将被忽略，因此节点x被查询区间覆盖条件为：

当x为根节点时，因其父节点fx不存在，令QL≤L(fx)≤R(fx)≤QR为假。

本文假定所有查询区间的出现概率相等。由式（1）可得出节点覆盖概率px的计算公式：

根据式（2），可由算法1计算节点覆盖概率。

算法1 CNCP（calculate node coverage probability）

输入：待计算节点x及其父节点fx。

输出：区间树中所有节点的覆盖概率px。

1.若x为根节点：

2.若x为其他节点：

3.对所有y∈Son(x)，执行CNCP(y,x)；

实际上，当查询区间满足其他分布特性时，通过对式（2）的调整，其节点覆盖概率亦可通过本算法进行计算。算法1仅要求树结构满足区间树定义，因此适用于任意树结构的差分隐私区间树。

3.2节点系数计算及隐私预算分配

在计算出节点覆盖概率后，即可据此调整隐私预算，通过异方差加噪方式降低整体的查询误差。而在此之前，需分析如何保证异方差加噪后的差分隐私区间树满足ε-差分隐私。

证明 对任意节点x，设Sub(x)表示以节点x为根节点的子树，A(x)表示对子树Sub(x)进行发布的算法，则：

根据结论1，若要保证异方差加噪后的区间树满足ε-差分隐私，需满足以下条件：

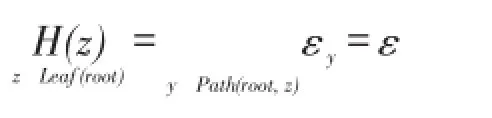
则区间计数查询误差期望：

因此，在满足ε-差分隐私的前提下，求解区间树上各节点的差分隐私预算，从而最小化区间计数查询误差期望的问题，可转化为以下最优化问题：

其中，εˉ表示区间树中节点的差分隐私预算向量。

下面通过定义4与结论2进行求解。

定义4（路径隐私预算和）

结论2为最小化区间计数查询误差期望（即求解式（3）），区间树中差分隐私预算分配方案需满足：

称ax、bx为节点x的节点系数，有:

证明（1）若x为叶节点，则结论2显然成立。

（2）若x为非叶节点，利用拉格朗日乘数法，可构造如下函数：

其中，λ为引入的未知标量。因目标函数 f(ε)为凸函数，同时求解式（3）与求解函数F(εˉ,λ)的全局最优解等价，因此将F(εˉ,λ)对εˉ求导，得：

假设对于y∈Son(x)，结论均成立，则：

对于节点SonBound(x)和任意 y∈Son(x)，在式（3）约束条件下，任意叶节点到根节点路径上的隐私预算和等于ε，因此：

由式（5）（6），得：

为满足式（4），必有：

将式（7）代入式（8）可得：

因此：

令

综合（1）（2），结论得证。

至此，可通过算法2计算节点系数ax、bx。

算法2 CNP（calculate node parameter）

输入：待计算节点x。

输出：区间树中所有节点的节点系数ax、bx。

1.若x为叶节点：ax←1,bx←1；

2.若x为其他节点：

3.对于y∈Son(x),运行CNP(y);

计算出节点系数ax、bx后，可通过算法3分配每个节点的差分隐私预算εx并进行异方差加噪。

算法3 NPBD（non-uniform private budget distribution）

输入：待加噪节点x，路径隐私预算和psum(x)。

3.对所有y∈Son(x)，执行：

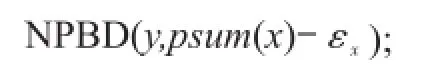
本文以图1所示差分隐私区间树为例，分析异方差加噪对区间计数查询精度的影响。

将图1所示区间树通过算法1及算法2进行节点覆盖概率和系数计算，结果如图2所示。再通过算法3进行隐私预算分配，得到各节点的隐私预算：

Fig.2　Example of non-uniform private budget distribution图2　异方差加噪示例

该方案与图1（b）所示一致。分别对图1（a）、图1 （b）中的隐私预算分配方案计算区间计数查询误差期望：

查询误差期望由原先同方差加噪的10.67，降低至异方差加噪的8.25，查询精度得到提高。

3.3异方差加噪下面向任意区间树结构的差分隐私直方图发布算法

上述步骤实现了对差分隐私区间树进行的异方差加噪。由于仅要求树结构满足差分隐私区间树定义，并无其他限定，该异方差加噪策略不仅适用于完全K叉树，还能够运用在任意区间树结构上。

任意树结构的差分隐私区间树示例如图3所示。

Fig.3　Range tree with different structures图3　不同树结构下的区间树

图3中，对于长度为22的直方图数据集而言，可采用如图3（a）的完全二叉树进行统计表示，也可用类似于图3（b）的任意树结构差分隐私区间树进行表示。对其分别计算区间计数查询误差期望：

可以看出，采用任意区间树结构之后，可以对树结构进行更灵活的调整，从而有效降低查询误差。结合异方差加噪方式，更能够进一步提升查询精度。

任意树结构差分隐私区间树的构建算法如下：

算法4 TSC（tree structure construct）

输入：待构建子树节点x，当前区间[l,r]。

输出：差分隐私区间树T。

在算法4中，对分支数K的选择和子区间长度的分配方式上进行改变，均会导致树结构的变化。树结构构建完成并进行节点覆盖概率计算（CNCP）、节点系数计算（CNP）和异方差加噪（NPBD）后，即可得到异方差加噪下的任意树结构差分隐私区间树。

在建立任意区间树并进行异方差加噪后，可有效提高区间计数查询精度。然而，通过如图4的示例可以发现，加噪后的区间树并不满足一致性约束。

Fig.4　Example of consistency constraintafter adding noise图4　加噪后造成的一致性约束问题示例

图4中，未加噪区间树（a）经加噪后，变为加噪区间树（b），其父节点1的计数值10.5与子节点计数值之和9.3不同，不满足一致性约束。以下将针对此问题，通过理论分析，证明异方差加噪下的任意区间树，仍可利用一致性约束进行最优线性无偏估计优化。

结论4差分隐私区间树从叶节点w到根节点路径上的节点线性无偏估计值hˉ满足下列公式：

证明 式(9)可转换为求解下式：

对于任意叶节点w，对hˉw求偏导：

结论5以节点x为根节点的子树中，节点x的估计值hˉx、叶节点到节点x的估计值加权和gˉx，均是关于叶节点的线性方程：

其中：

Bound(x)是以x为根节点的子树中第一个叶节点，w= SonBound(x)。

证明 定义节点高度：

（1）若节点x∈{y|Height(y)=0}，即x∈Leaf(root)，结论5显然成立。

（2）假设对任意节点y∈{y|Height(y)≤n}，式（11）均成立。当Height(x)=n+1时：

令hsum(x)表示从叶节点x到根节点路径上节点集合的加噪值加权和，由结论4可知：

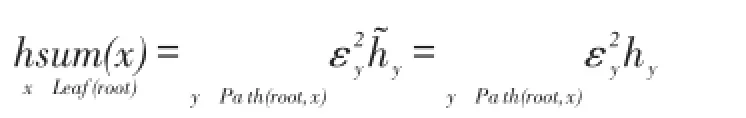
令w=SonBound(x)，由式（12）可知，对于节点y∈Son(x)，有Height(y)≤n，Height(w)≤n，且根据结论4，有：

代入式(11)可得：

由一致性约束可得：

综合（1）（2），证明式（11）成立。

经由以上结论及证明，通过维护参数(α,β,c,d)的值，并利用式（11）进行估计值计算，设计了对差分隐私区间树加噪后，在任意区间树结构下，利用最优线性无偏估计进行调整的优化算法。

算法5 PA_BLUE（parameter adjust using best linear unbiased estimate）

输入：待计算发布计数值的节点x。

输出：区间树所有节点的参数(α,β,c,d)。

1.若x为叶节点，更新：

并结束算法

计算参数(α,β,c,d)后，通过算法6计算优化后的最终发布值。

算法6 CRC（calculate range count）

输入：待计算发布计数值的节点x，令tot为

输出：区间树所有节点的发布计数值hˉx。

通过以上步骤，本文提出了异方差加噪下，面向任意区间树结构进行最优线性无偏估计优化的差分隐私直方图发布算法。

算法7 LUE-DPTree（linear unbiased estimator for differential private tree）

输入：原始直方图H，差分隐私参数ε。

输出：异方差加噪，任意树结构的ε-差分隐私区间树T_Publish。

下面对算法7的差分隐私保障和算法复杂度进行分析证明。

结论6算法7所生成的差分隐私区间树T_publish满足ε-差分隐私。

证明 对于区间树T_Publish，由式（3）中的约束条件可知，在计算各节点隐私预算εx时，始终在该约束下进行：

由结论1可知，整体发布过程满足ε-差分隐私。

结论7算法7的算法时间复杂度、空间复杂度均为O(n)。

证明 在算法7中，各步骤均为对区间树进行一次扫描，时间复杂度为O(n)。在CNCP、CNP和PA_BLUE算法中，分别需存储各节点的节点覆盖概率、节点系数等值，空间复杂度为O(n)。在TSC、NPBC、CRC算法中，分别对树节点的发布值进行计算及改变，空间复杂度同样为O(n)。因此，算法7的时间、空间复杂度均为O(n)，为线性复杂度。

4　实验结果与分析

本文从区间计数查询精度和算法运行效率两方面与同类代表算法Boost[8]进行对比分析。在文献[10]中，提出了在区间树的不同层次间进行异方差分配的迭代方法，本文将其应用于Boost算法中，并标识为Boost-UN。同时，为了更好地体现本文算法的有效性，实验也与基于小波变换的Privelet[15]算法进行了比较分析。同样采用了异方差加噪方式的算法DP-tree[11]，由于并未给出具体算法描述，从而未与其进行实验对比。在实验中，隐私参数ε取值分别为{1.0，0.1，0.01}。采用如式（13）所示的平均方差进行误差衡量。为使实验结果更具一般性，取算法执行50次的平均值作为最终结果。

其中，q(T)为区间计数查询的真实结果；q(T′)为区间计数查询的加噪计数值； ||Q为查询集大小。

4.1实验环境

为便于对比分析，采用了与文献[8]相同的实验数据集Social Network、Search Logs、NetTrace进行实验。Social Network数据集记录了某在线社交平台的用户关系无向图中具有特点度的用户数。Search Logs数据集统计了2004年1月至2009年8月期间，关于“Obama”关键词的搜索频率。NetTrace数据集对某大学在一个时间段内的IP数据包信息进行了记录。其数据规模如表1所示。

实验硬件环境为：Intel Core i7 930 2.8 GHz处理器，4 GB内存，Windows 7操作系统。算法实现采用C++语言，由Matlab生成实验图表。

Table 1　Dataset size表1 数据集规模

4.2查询精度

本文通过与Boost、Privelet等算法的对比，分析LUE-DPTree在区间计数查询精度上的表现。并通过对树结构的调整，分析不同树结构对查询精度的影响。

4.2.1与Boost、Privelet等算法的对比

本文分别采用随机任意长度区间和随机固定长度区间两种方式，对算法查询精度进行检验。其中，任意长度区间随机生成1 000条，区间的起点L和终点R随机生成，且L≤R。随机固定长度的区间，区间大小分别取20,21，…，213，…，每种长度随机生成1 000条查询区间。考虑到Boost和Privelet算法适用于2的整数幂的数据规模，在这部分实验中，仅选取Search Logs和NetTrace为实验数据集。

在图5和图6的实验对比结果中，随隐私参数ε的减小，平均误差约按102的量级增长。在4种算法中，LUE-DPTree算法的查询精度较优。说明异方差加噪策略和一致性约束下的最优线性无偏估计优化，有效提高了算法的区间计数查询精度。

在图7和图8中，固定区间大小的随机查询，其误差随区间大小增加而增大。在各区间长度下，LUE-DPTree算法的查询精度均优于Boost和Privelet算法。而Boost-UN算法中，采用异方差加噪方式，仅在不同层次中进行了隐私预算分配，而在同一层次的节点中，仍采用了相同的隐私预算，因此查询精度介于Boost和LUE-DPTree算法之间。该实验结果说明，LUE-DPTree算法中的隐私预算分配策略，在能够适用于任意区间树结构，提供更高灵活度的同时，还能更有效地提升查询精度。

综合上述实验分析表明，相比其他两种算法，LUE-DPTree算法具有更高的数据发布质量。

4.2.2不同区间树结构对精度的影响

为观察不同区间树结构对查询精度的影响，选取了4种树结构：2叉树、3叉树、4叉树和任意叉树（每次随机分2～4叉）分别标识为LUE-DPTree-2、LUE-DPTree-3、LUE-DPTree-4、LUE-DPTree-R。为方便起见，这部分实验仅选取ε=1.0时，LUE-DPTree算法在Social Network和NetTrace两个数据集上的结果进行对比。

Fig.5　Comparison of random range queries error in Search Logs图5　随机任意长度区间的查询误差对比(Search Logs)

Fig.6　Comparison of random range queries error in NetTrace图6　随机任意长度区间的查询误差对比(NetTrace)

Fig.7　Comparison of random range queries error under different lengths in Search Logs图7　不同区间大小下的查询误差曲线图(Search Logs)

Fig.8　Comparison of random range queries error under different lengths in NetTrace图8　不同区间大小下的查询误差曲线图(NetTrace)

从图9中可以观察到，在Social Network数据集上，不同树结构的查询精度差别较大，相比其他结构，任意叉树结构的查询精度更高；而在NetTrace数据上，精度差别较小，2叉树结构相比其他结构有更小的误差。结果说明，对于不同特征的数据集，若要更好地提高数据发布质量，需要建立不同的树结构，包括任意区间树结构。Boost算法仅适用于完全K叉树的情况，使得人们无法通过改变树结构来降低查询误差。而LUE-DPTree算法则可以适用于任意区间树结构，使得人们可以有更大的调整空间，能够寻找更佳的构建方式来进一步提高直方图发布的质量。

Fig.9　Comparison of random range queries error of LUE-DPTree under different range tree structures图9　LUE-DPTree算法在不同区间树结构下的查询误差

Fig.10　Comparison of average running time under differentε图10　不同隐私参数ε下的平均运行时间

4.3算法运行效率

本文通过以下方案对比分析4种算法在不同情况下的运行效率：（1）在树结构相同，数据集和隐私参数取值不同的情况下分析4者的运行效率。（2）在隐私参数和数据集相同，树结构不同的情况下分析LUE-DPTree算法的运行效率。同样考虑到Boost和Privelet算法对树结构的要求，在实验（1）中仅采用Search Logs和NetTrace两个数据集。在实验（1）中，隐私参数ε分别取值1.0、0.1、0.01，在实验（2）中取值1.0。为使结果更具可比性，在实验（1）中树结构采用完全2叉树结构，在实验（2）中LUE-DPTree分别选择2叉树、3叉树、4叉树和任意叉树（每次随机分2～4叉）。运行时间不包含数据读入和查询时间。实验结果分别如图10和图11所示。

Fig.11　Comparison of average running time of LUEDPTree under different tree structures图11 不同树结构下LUE-DPTree算法的平均运行时间

从图10中可以得出：（1）4种算法的运行时间均随着数据规模的增大而增大，与数据规模成比例增加。（2）由于4种算法的运行效率与隐私参数无关，运行时间基本不随隐私预算改变而变化。相比其他算法，LUE-DPTree算法多进行了一次隐私预算分配的过程，因此运行时间稍长于另外3种算法。

从图11中可以看出，LUE-DPTree算法的运行时间随着树结构的变动而变动，基本与差分隐私区间树的节点数量成正相关，与结论7所分析的线性复杂度相符。

总体来说，LUE-DPTree算法与Boost、Privelet算法均具有较高的运行效率。LUE-DPTree算法的运行效率虽略差于同类经典算法，但仍具较高的性能。

5　结束语

本文提出了一种异方差加噪下面向任意区间树结构的差分隐私直方图发布算法，该算法能够在保证运行效率的前提下，有效降低查询误差。相比采用特定区间树结构的发布算法，该算法适用于任意区间树结构，在树结构上有更大的调整灵活度，而异方差加噪方式，也为在不同的查询规律、数据特性下进行查询精度提升提供了更大的优化空间，因此该算法具有更好的灵活性。同时，由于任意树结构放宽了对数据集长度的限制，提高了算法的适用范围，使得算法具有更高的实用性。

在接下来的研究工作中，将考虑如何更加合理地通过数据分布情况和查询区间规律，设计启发式的区间树构建方法与隐私预算分配方式，进一步提高发布数据的质量。

References:

[1]Zhou Shuigeng,Li Feng,Tao Yufei,et al.Privacy preservation in database applications:a survey[J].Chinese Journal of Computers,2009,32(5):847-861.

[2]Xiong Ping,Zhu Tianqing,Wang Xiaofeng.A survey on diafaferential privacy and applications[J].Chinese Journal of Computers,2014,37(1):101-122.

[3]Zhang Xiaojian,Meng Xiaofeng.Differential privacy in data publication and analysis[J].Chinese Journal of Computers, 2014,37(4):927-949.

[4]Sweeney L.k-anonymity:a model for protecting privacy[J]. International Journal on Uncertainty,Fuzziness and Knowledge Based Systems,2002,10(5):557-570.

[5]Machanavajjhala A,Gehrke J,Kifer D,et al.l-diversity:privacy beyond k-anonymity[C]//Proceedings of the 22nd International Conference on Data Engineering,Atlanta,USA, Apr 3-8,2006.Piscataway,USA:IEEE,2006:24-35.

[6]Dwork C.Differential privacy[C]//Proceedings of the 33rd International Colloquium on Automata,Languages and Programming,Venice,Italy,Jul 10-14,2006.Berlin,Heidelberg:Springer,2006:1-12.

[7]Acs G,Castelluccia C,Chen Rui.Differentially private histogram publishing through Lossy compression[C]//Proceedings of the 12th IEEE International Conference on Data Mining,Brussels,Belgium,Dec 10-13,2012.Piscataway, USA:IEEE,2012:84-95.

[8]Hay M,Rastogi V,Miklau G,et al.Boosting the accuracy of differentially private histograms through consistency[J]. Proceedings of the VLDB Endowment,2010,3(1):1021-1032.

[9]Xu Jia,Zhang Zhenjie,Xiao Xiaokui,et al.Differentially private histogram publication[J].The VLDB Journal,2013, 22(6):797-822.

[10]Qardaji W,Yang Weining,Li Ninghui.Understanding hierarchical methods for differentially private histograms[J]. Proceedings of the VLDB Endowment,2013,6(14):1954-1965.

[11]Peng Shangfu,Yang Yin,Zhang Zhenjie,et al.DP-tree:indexing multi-dimensional data under differential privacy[C]// Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data,Scottsdale,USA,May 20-24,2012.New York,USA:ACM,2012:864.

[12]Dwork C,McSherry F,Nissim K,et al.Calibrating noise to sensitivity in private data analysis[C]//LNCS 3876:Proceedings of the 3rd Theory of Cryptography Conference, New York,USA,Mar 4-7,2006.Berlin,Heidelberg:Springer, 2006:265-284.

[13]McSherry F,Talwar K.Mechanism design via differential privacy[C]//Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science,Providence, USA,Oct 21-23,2007.Piscataway,USA:IEEE,2007:94-103.

[14]Ghosh A,Roughgarden T,Sundararajan M.Universally utility-maximizing privacy mechanisms[C]//Proceedings of the 41st Annual ACM Symposium on Theory of Computing,Betheda,USA,May 31-Jun 2,2009.New York,USA: ACM,2009:351-360.

[15]Xiao Xiaokui,Wang Guozhang,Gehrke J.Differential privacyviawavelettransforms[J].IEEETransactionson Knowledge and Data Engineering,2011,23(8):1200-1214.

附中文参考文献：

[1]周水庚,李丰,陶宇飞,等.面向数据库应用的隐私保护研究综述[J].计算机学报,2009,32(5):847-861.

[2]熊平,朱天清,王晓峰.差分隐私保护及其应用[J].计算机学报,2014,37(1):101-122.

[3]张啸剑,孟小峰.面向数据发布和分析的差分隐私保护[J]计算机学报,2014,37(4):927-949.

KANG Jian was born in 1989.He is an M.S candidate at College of Mathematics and Computer Science,Fuzhou University.His research interest is differential privacy preserving.

康健（1989—），男，福建漳州人，福州大学数学与计算机科学学院硕士研究生，主要研究领域为差分隐私保护。

WU Yingjie was born in 1979.He received the Ph.D.degree in computer science from Southeast University in 2012.Now he is an associate professor at Fuzhou University.His research interests include data mining,data security and privacy preserving,etc.

吴英杰（1979—），男，2012年于东南大学计算机科学专业获得博士学位，现为福州大学副教授，主要研究领域为数据挖掘，数据安全与隐私保护等。

HUANG Siyong was born in 1989.He received the M.S.degree from Fuzhou University in 2015.His research interest is differential privacy preserving.

黄泗勇（1989—），男，福建漳州人，2015年于福州大学获得硕士学位，主要研究领域为差分隐私保护。

CHEN Hong was born in 1989.He received the M.S.degree from Fuzhou University in 2014.His research interest is differential privacy preserving.

陈鸿（1989—），男，福建长乐人，2014年于福州大学获得硕士学位，主要研究领域为差分隐私保护。

SUN Lan was born in 1978.She received the M.S.degree from Xi’an Jiaotong University in 2003.Now she is a lecturer at Fuzhou University.Her research interests include data security and privacy preserving.

孙岚（1978—），女，陕西西安人，2003年于西安交通大学获得硕士学位，现为福州大学讲师，主要研究领域为数据安全与隐私保护。

*The National Natural Science Foundation of China under Grant No.61300026(国家自然科学基金);the Natural Science Foundation of Fujian Province under Grant No.2014J01230(福建省自然科学基金).

Received 2015-07,Accepted 2015-09.

CNKI网络优先出版:2015-09-15,http://www.cnki.net/kcms/detail/11.5602.TP.20150915.1630.010.htmlqueries and the algorithm efficiency.The experimental results show that LUE-DPTree is effective and feasible.

+Corresponding author:E-mail:yjwu@fzu.edu.cn

文献标志码：A

中图分类号：TP311

doi:10.3778/j.issn.1673-9418.1507067

Algorithm for Differential Privacy Histogram Publication with Non-uniform Private Budgetƽ

KANG Jian,WU Yingjie+,HUANG Siyong,CHEN Hong,SUN Lan
College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,China

Abstract:Most of existing methods for differential privacy histogram publication based on range tree adopt a uniform private budget.However,it is found that the accuracy of range queries can be further enhanced if using a non-uniform private budget.Unfortunately,current techniques for differential privacy histogram publication with non-uniform private budget require strict range tree structure,which lowers its flexibility and practicability.This paper proposes an algorithm LUE-DPTree(linear unbiased estimator for differential private tree)for differential privacy histogram publication with non-uniform private budget under arbitrary range tree structure.The key idea of LUE-DPTree is to firstly calculate the query coverage probability of range tree nodes based on the distribution of range counting queries so as to allocate the non-uniform private budget.After that,it is shown by further analysis that the strategy of non-uniform private budget can be used in arbitrary range tree.Furthermore,it is indicated by theoretical proof that,after allocated non-uniform private budget under arbitrary range tree structure,the error of range counting queries still can be further reduced by solving the best linear unbiased estimators of the tree nodes’values through consistency constraint.The experimental analysis is designed by comparing LUE-DPTree and the traditional algorithms on the accuracy of range counting

Key words:privacy preserving;differential privacy;histogram publication;non-uniform private budget;range tree