Symmetric Periodic Orbits and Uniruled Real Liouville Domains∗

Urs FRAUENFELDER Otto van KOERT

1 Introduction

For closed symplectic manifolds,Hu,Li and Ruan[8]have defined the notion of symplectical uniruledness by requiring the existence of a non-zero Gromov-Witten invariant of genus zero with a point constraint(see[8]).It was pointed out by Li[9],that it is not meaningfulto naively mimic the definition of algebraic geometry,since he showed that for a simply-connected,closed symplectic manifold,there always exists a symplectic surface in a suitable fixed homology class going through a point.On the other hand,for Liouville domains,there are no nonconstant holomorphic spheres,and McLean proposed to use holomorphic planes instead(see[14]).Roughly speaking,these holomorphic planes are asymptotic to periodic Reeb orbits,and therefore play an important role in the dynamics on the boundary of the Liouville domains.For instance,Hofer-Viterbo and Lu used a stretching construction involving related ideas to prove versions of the Weinstein conjecture(see[4,11]).

Many interesting symplectic manifolds come equipped with a symmetry in the form of an anti-symplectic involution,also known as a real structure.In that case,one can investigate holomorphic curves that are invariant under this involution to get more specialized information.In the case of closed symplectic manifolds,this was done by Welschinger[20]in the form of real Gromov-Witten invariants and it is the subject of ongoing research(see for instance[3]).Therefore it is also natural to investigate the notion of uniruledness for Liouville domains that have such a symmetry.An application of this notion consists of existence results for symmetric periodic Reeb orbits.

We will now state our notions and results more precisely.We define a real Liouville domain(W,λ,?)as a triple consisting of a Liouville domain(W,λ)and an exact anti-symplectic involutionDiff(W),i.e.,a map?satisfying

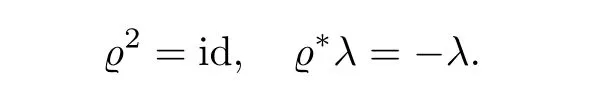
If we restrict e to the boundary∂W of the Liouville domain W,we get a real contact manifold,meaning a contact manifold together with an involution,under which the contact form is antiinvariant.If R denotes the Reeb vector field on∂W,then R is anti-invariant under e as well,i.e.,

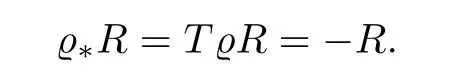
If T>0 and v∈ C∞([0,T],∂W)is a T-periodic orbit for R,then v?∈ C∞([0,T],∂W)defined as

is a T-periodic orbit as well.

Definition 1.1AT-periodic orbitv ∈ C∞([0,T],∂W)is called symmetric if it satisfiesv=v?.

Symmetric periodic orbits play a prominent role in the restricted three body problem(see[2])as well as in the Seifert conjecture on brake orbits(see[19]).

The Weinstein conjecture asserts that on every closed contact manifold,the Reeb flow admits a periodic orbit.Affirmative answers to this conjecture can be obtained in various cases by taking advantage of the interplay between holomorphic curves and closed Reeb orbits(see[4,10–11,21]).To examine this connection in the real case,we introduce the notion of an uniruled real Liouville domain.Note that for a real Liouville domain(W,λ,?),the Liouville vector field X defined by the equation ιXdλ = λ is invariant under?and therefore?extends to the completion V of W.By abuse of notation,we will also use the symbols λ and?for the extensions to V.If we choose on V an SFT-like almost-complex structure anti-invariant under?,then?induces an involution of finite energy planes on V.Inspired by the paper of McLean[14],we give the following definition.

Definition 1.2A real Liouville domain(W,λ,?)is called(real)uniruled if for every antiinvariant SFT-like complex structureJon the completion(V,λ,?),there exists an invariantfinite energy plane of SFT-energy less than or equal to1through any given point on the La-grangian submanifoldFix(?)⊂V.

Note that the above consists of a requirement for every anti-invariant complex structure J,which makes this notion meaningful.In particular,there are real Liouville domains without any finite energy plane for any SFT-like complex structure,such as the disk bundle D∗Σgassociated with a hyperbolic metric on a surface of higher genus.For a simply-connected example,consider the affine part of Fermat-type hypersurfaces,

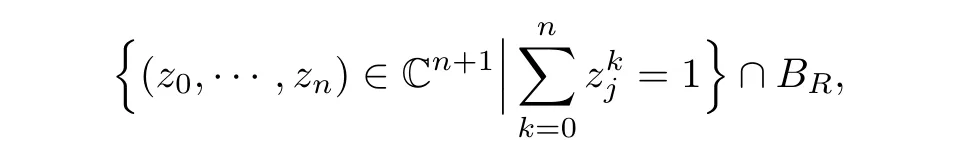
where BRis a ball of sufficiently large radius R.If the degree k is larger than 3n−2,then the Fredholm index of any finite energy plane is negative.This implies that for a generic choice of the SFT-like complex structure,no finite energy planes exist,and hence such an affine hypersurface is in particular not uniruled.Alternatively,one could use the real Gromov-Witten theory,developed in[20],to formulate the above notion.

The asymptotic behavior of finite energy planes as studied in[5–7,16]immediately implies the following theorem.

Theorem 1.1Assume that(W,λ,?)is a uniruled real Liouville domain.Then there exists a symmetric periodic orbit of the Reeb vector fieldRon∂Wof period less than or equal to1.

Remark 1.1If one requires that the SFT-energy of the invariant finite energy planes in Definition 1.2 is less than or equal to a constant κ>0 instead of being less than or equal to 1,the period of the symmetric Reeb orbit in Theorem 1.1 can be estimated from the above by the constant κ.However,we can always scale λ toλ so that one does not gain anything by considering this more general notion.

The purpose of this note is to provide a condition which guarantees uniruledness for a real Liouville domain.For this,we embed the real Liouville domain into a closed symplectic manifold and use the Gromov-Witten theory on this ambient manifold.One could use Welschinger’s invariants(“real Gromov-Witten theory”)as are used for instance in[20],but we will argue indirectly.Let us now explain the properties we require on the ambient manifold.

Assume that(M,ω)is a closed symplectic manifold that satisfies the Bohr-Sommerfeld condition,that is,the cohomology class represented by the symplectic form is integral in the sense that the class[ω]lies in the image of H2(M;Z)in H2(M;R).We suppose in addition that[ω]is primitive in the sense that for every k>1,the cohomology class[ω]is not integral.

Definition 1.3We say that a symplectic hypersurfaceΣ ⊂ Mis primitive if[Σ]is Poincar´e dual to[ω].

Remark 1.2If H2(M;Z)is torsion-free,this notion is unambiguous.If H2(M;Z)has torsion,the class[ω]∈(M)does not uniquely determine an integral cohomology class.In this latter case,we mean that[Σ]is Poincar´e dual to[ω]when regarded as a real homology class in H2n−2(M;R).

Denote by h:π2(M)→ H2(M;Z)the Hurewicz homomorphism.

Definition 1.4We say that a classA∈im(h)is decomposable if there exist classesB,C∈im(h)satisfying

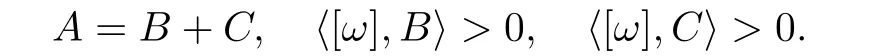
We say thatAis indecomposable if it is not decomposable.

Definition 1.5A decorationD=(Σ,A,S)of(M,ω)is a triple consisting of a primitive symplectic hypersurfaceΣ ⊂ M,an indecomposable homology classA ∈ H∗(M)and a submanifoldS⊂Σsatisfying the following two requirements:

(i)A◦[Σ]=1.

(ii)The Gromov-Witten invariantGWA([S],[p])is odd,where[p]is the homology class of a point.

We refer to the triple(M,ω,D)as a decorated symplectic manifold.

Remark 1.3By Gromov-Witten invariants we mean the variants defined in[13],and for this we insist that S should be a submanifold rather than a general cycle.

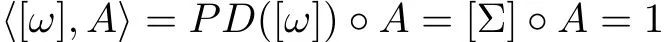
Remark 1.4Note that for a decoration D=(Σ,A,S),we have so that each holomorphic sphere contributing to the Gromov-Witten invariant GWA([S],[p])has a symplectic area equal to 1.

Definition 1.6Assume that(M,ω,D)is a decorated symplectic manifold with decorationD=(Σ,A,S).An anti-decorating involutionρ:M → Mis an anti-symplectic involution satisfying the following conditions:

(i)BothΣandSare invariant underρ.

(ii)ρ∗A= −A.

A decorated real symplectic manifold(M,ω,D,ρ)is a quadruple consisting of a decorated symplectic manifold(M,ω,D)together with an anti-decorating involutionρ.

Definition 1.7Assume that(W,λ,?)is a real Liouville domain and(M,ω,D,ρ)is a decorated real symplectic manifold.An embedding of a real Liouville domain into a decorated symplectic manifold

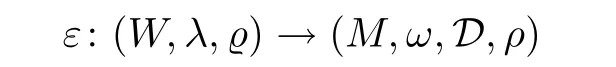
is an embeddingε:W → MΣsatisfying

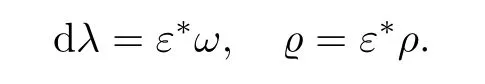
A Christmas tree is a quadruple(W,λ,ρ,ε)consisting of a real Liouville domain(W,λ,ρ)and an embeddingε:(W,λ,ρ)→ (M,ω,D,ρ)into a decorated real symplectic manifold.

The main result of this paper is the following theorem.

Theorem 1.2Assume that(W,λ,ρ,ε)is a Christmas tree satisfyingb1(W)=0.Then(W,λ,ρ)is real uniruled.

Combining Theorem 1.2 with Theorem 1.1,we obtain the following corollary.

Corollary 1.1Assume that(W,λ,ρ,ε)is a Christmas tree satisfyingb1(W)=0.Then there exists a symmetric periodic orbit of a period less than or equal to1for the Reeb flow on∂W.

2 Definitions and Notions of the Symplectic Field Theory(SFT for short)

By a real symplectic manifold we mean a triple(M,ω,ρ)where(M,ω)is a symplectic manifold and ρ∈Diff(M)is an anti-symplectic involution,so

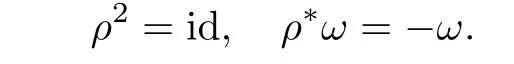
A Liouville domain is a compact exact symplectic manifold(W,ω =dλ)with a global Liouville vector field,defined by ιXω = λ,such that the boundary is smooth and convex,meaning that the Liouville vector field X points outward at the boundary.

The boundary of a Liouville domain carries a natural cooriented contact structure.Indeed,the Liouville condition implies that α := λ|∂Wis a positive contact form on ∂W,so α ∧(dα)n−1>0.The hyperplane distribution defined by

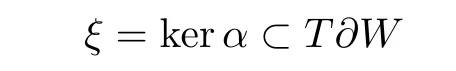
is called the contact structure and the vector field R on∂W defined by the equations is called the Reeb vector field.

The following procedure can be used to complete a Liouville domain W into a so-called Liouville manifold,which has cylindrical ends instead of convex boundary components.For each boundary component C of∂W,we attach the positive end of a symplectization,given by the symplectic manifold([0,∞[×C,d(etα)),to W along C.The Liouville vector field on the cylindrical end is

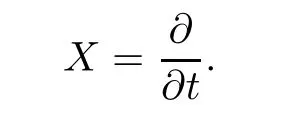
After this process we obtain a complete Liouville manifold,which we will denote by(V,λ).

An almost-complex structure J on a complete Liouville manifold V is called compatible with the symplectic form ω =dλ if ω(·,J·)is a Riemannian metric.An ω-compatible almost-complex structure J is called SFT-like if it satisfies the following conditions:

(1)J preserves the hyperplane distribution ξ on ∂W ⊂ V.

(2)On∂W it rotates the Liouville vector field into the Reeb vector field in the sense that JX=R and JR=−X.

(3)On the cylindrical end∂W ×[0,∞[the almost-complex structure is invariant under the Liouville flowfor t∈ [0,∞).

Pick an SFT-like almost-complex structure J on V and assume that w:(C,i)→(V,J)is a J-holomorphic plane.We now explain how to define the energy of w.This will be a variation of the Hofer energy.Choose a small δ>0,indicating the size of a collar neighborhood of∂W,and define

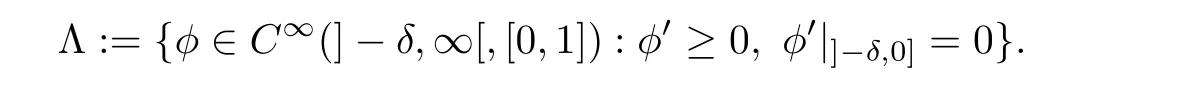
For φ ∈ Λ,define a 1-form λφ∈ Ω1(V)by

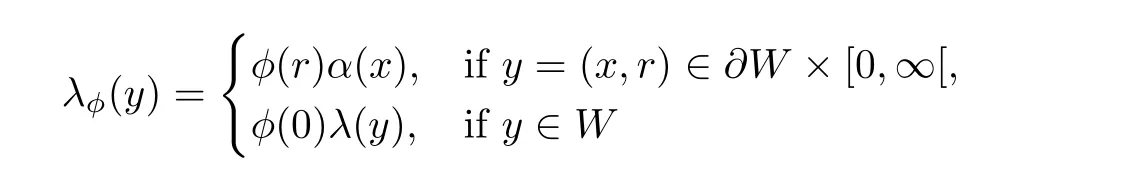
and abbreviate ωφ=dλφ.The Hofer energy or SFT energy of w is then defined as

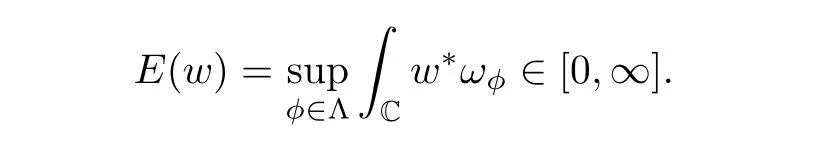
The holomorphic plane w is called a finite energy plane if it satisfies

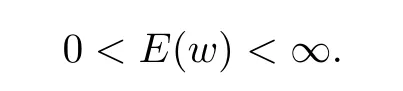
We also have the following non-real version of uniruledness,somewhat different from[14].

Definition 2.1We call a Liouville domain(W,λ)uniruled if for every SFT-like almostcomplex structureJon its completion(V,λ),there exists a finite energy plane through every point ofV.

3 Examples of Christmas Trees

In this section,we will discuss some examples of Christmas trees.An interesting example concerns the canonical contact form and structure on the unit cotangent bundle of a sphere,(T∗Sn,λcan,ρ),which can be embedded as a real Liouville manifold into the projective quadric with various anti-symplectic involutions ρ.We will check that the projective quadric can be decorated by computing a suitable Gromov-Witten invariant.Real Liouville structures on T∗S2include the regularized,planar circular restricted three-body problem(see[1]),which has one anti-symplectic involution,and the Hill’s lunar problem,which has two commuting anti-symplectic involutions.

Before we verify the decoration requirements for the quadric,we start by giving the following basic lemma.

Lemma 3.1Let(M,ω,D=(Σ,A,B))be a decorated symplectic manifold with an antidecorating involutionρ.ThenM − νM(Σ)carries the structure of a real Liouville domain,whereνM(Σ)denotes a tubular neighborhood ofΣinM.

ProofWe first show that W:=M − νM(Σ)is an exact symplectic manifold.For this,consider the long exact sequence of the pair in cohomology,

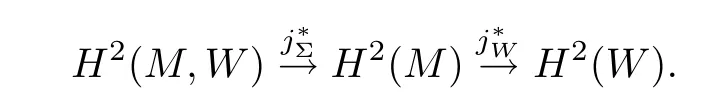
By Corollary 11.2 of[15],the cohomology ring H∗(M,W)is canonically isomorphic to the cohomology ring H∗(νM(Σ),νM(Σ)0),associated with the normal bundle of Σ.Here νM(Σ)0denotes the normal bundle of Σ with its zero-section removed.Thus the Thom class u∈H2(νM(Σ),νM(Σ)0)corresponds to a class u'in H2(M,W).As the homology class[Σ]is Poincar´e dual to[ω](over the reals),it follows thatequals[ω]by Problem 11-C from[15].By exactness of the long exact sequence of the pair,we see=0,so there exists a 1-formsuch that dλ = Ω := ω|W.

We now show that we can choose a real Liouville form,i.e.,.Since dλ=Ω and ρ∗Ω = −Ω,we see that there exists a closed 1-form μ such that

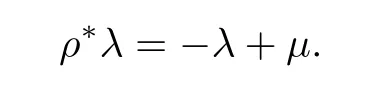
Since λ=ρ∗◦ ρ∗λ=λ − μ+ρ∗μ,we see that μ=ρ∗μ.DefineThenHenceis the desired real Liouville domain.

3.1 Smooth quadrics in a projective space

We define a quadric in a projective space as the zero-set of a non-zero homogeneous quadratic polynomial.Note that a homogeneous quadratic polynomial can always be written as p(z)=ztBz,where B is a symmetric matrix.By Sylvester’s theorem,we can assume that B is diagonal.We then easily see the following result.

Lemma 3.2A quadric is smooth if and only ifBhas the maximal rank.

We have the following identification of the smooth projective quadric with an oriented Grassmannian.

Lemma 3.3The smooth projective quadric given by

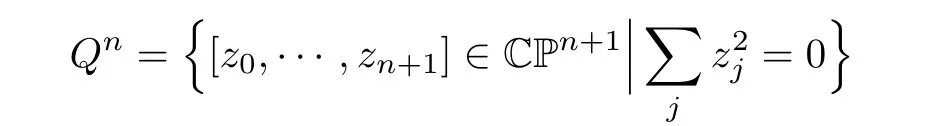
is diffeomorphic to the symmetric spaceFurthermore,SO(n+

2)acts transitively via biholomorphisms.

ProofFor the first part,we exhibit the diffeomorphism

where x,y∈Rn+2form an orthonormal basis of the 2-plane they span.We use thatTo see that SO(n+2)acts by biholomorphisms,just observe that

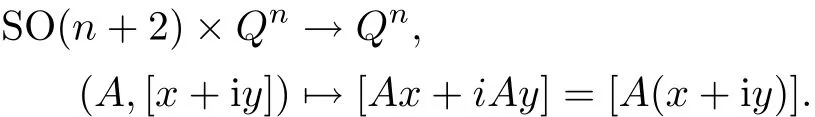
By an affine quadric we mean the zero-set of a non-zero quadratic polynomial in Cn+1.Away from possible singular points,an affine quadric inherits a symplectic structure as a complex submanifold of a Kähler manifold.It is well-known(see[12,Exercise 6.20]),that a smooth affine quadric is symplectomorphic to T∗Snwith its canonical symplectic structure.

Lemma 3.4There is a symplectomorphism

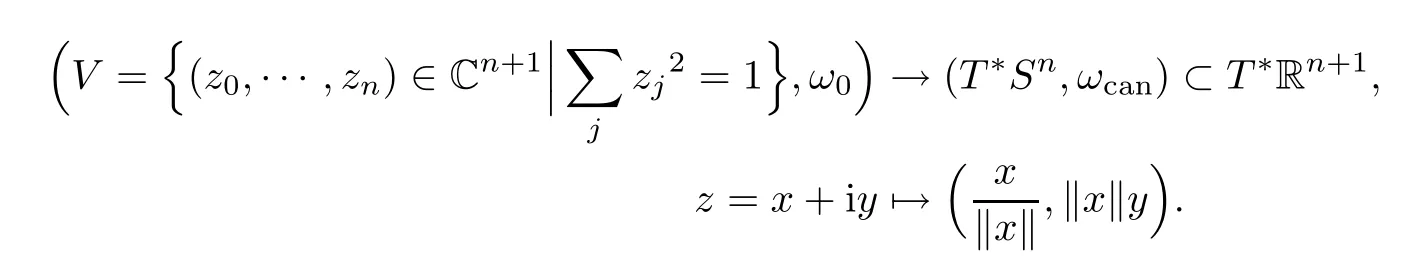
The singular affine quadric appearing in the following lemma is also of interest.

Lemma 3.5The symplectization of(ST∗Sn,λcan)is symplectomorphic to

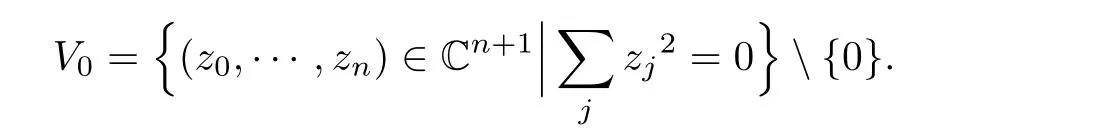
In addition,the standard complex structureiis an SFT-like complex structure for the symplectization.

3.2 Naive Gromov-Witten invariants of quadrics

We consider a smooth quadric Qngiven as the zero locus of the symmetric bilinear form B.The Lefschetz hyperplane theorem implies that for n>2,we have H2(Qn;Z)Z(see[12,Example 4.27]).Moreover,this homology group is generated by a line L,by which we mean a map of the form[λ :μ]∈ CP1→ λp+μq,where p,q ∈ Qn⊂ CPn+1(so B(p,p)=B(q,q)=0)and B(p,q)=0.The quadric Q2in 4-dimensions is diffeomorphic to S2×S2,so H2(Q2;Z)Z2,and there are two types of lines,distinguished by their homology classes.We will equip Qnwith its natural complex structure J0.

Let Hol(J0,[L])denote the space of J0-holomorphic maps from CP1to Qnrepresenting the homology class[L].Write M(J0,[L])for the moduli space of J0-holomorphic curves with the homology class[L].We have

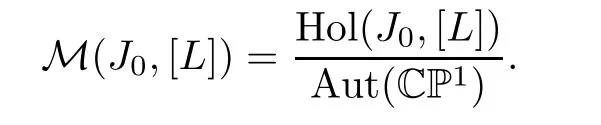
We will compute some Gromov-Witten invariants by “naive counting” (see[18]).To show that this works,we need to establish the regularity of J0.

3.3 Moduli space and regularity

Let L be a line on a smooth projective quadric with a primitive homology class[L]∈H2(Qn;Z).We linearize the Cauchy-Riemann equations at a parametrization of L given by u:CP1→Qn.

Lemma 3.6The linearized operator atuis surjective.In particular,the space of holomorphic mapsHol(J0,[L])inQnis a smooth manifold of dimensiondimHol(J0,[L])=2n+2n.

We give two arguments for this statement.

3.3.1 Regularity via sheaves and splitting of the normal bundle

In the language of sheaves,triviality of the cokernel is equivalent to vanishing of the sheaf cohomology group H1(L,T Qn|L)(see the statement of Riemann-Roch).We have the short exact sequence of sheaves

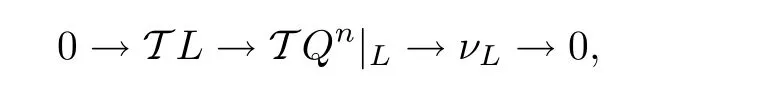
where νLis the sheaf of germs of holomorphic sections of the normal bundle of L.A piece of the corresponding long exact sequence in cohomology looks like

It is a well-known classical fact that H1(CP1,O(k))=0 for k≥ −1(a generalization of this formula is known as the Bott formula(see[17,Chapter 1]),so we see directly that H1(L,T L)=0 as T LO(2).For the normal bundle,note that a line L in a smooth quadric Qnis always contained in a tower of smooth quadrics of the form

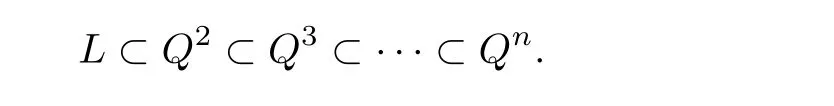
The normal bundle νQk(Qk−1)is isomorphic to O(1),and the normal bundle νQ2(L)is trivial,so νLsplits as

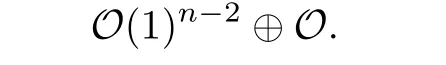
By the earlier mentioned Bott formula H1(L,νL)H1(CP1,O(1))⊕n−2⊕ H1(CP1,O)=0,we conclude that H1(L,T Qn|L)=0.

3.3.2 Regularity via holomorphic transitive actions

Lemma 3.3 tells us that we have a holomorphic transitive action on Qn,so by[13,Proposition 7.4.3],every holomorphic sphere is regular,and the claim of the lemma follows.

3.4 Lines through a point

Now consider the evaluation map

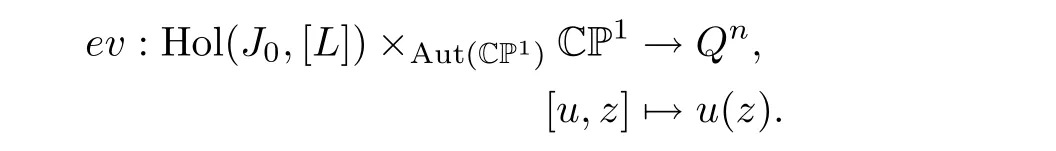
By Sard’s theorem we find a regular value p of ev,and in fact,since SO(n+2)acts transitively on Qn,every value is regular.Define the moduli space of lines through p as Mp=ev−1(p).

Geometrically,we can describe Mpas follows.If L=pq is a line through p and q which is completely contained in Qn,then B(λp+ μq,λp+ μq)=0 for all[λ :μ]∈ CP1.This gives a quadratic equation in λ and μ,which should vanish identically,so by looking at the coefficients,we find

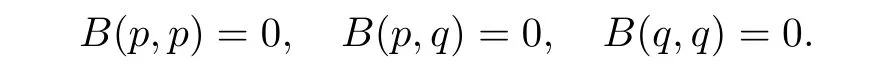
As p and q lie on Qn,we automatically have B(p,p)=0=B(q,q).The remaining equation defines a hyperplane in CPn+1,namely,the “geometric tangent plane”

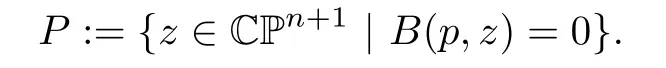
Since every line through p intersects the quadric at in finity,which is given by Q∞={z=[z0:···:zn:0]|z∈ Qn},we can identify the moduli space of lines through p with Mp=Q∞∩P.

To obtain a Gromov-Witten invariant,we will consider lines through p going through an additional cycle C.First define

A dimension count tells us that C should be a 2-cycle if we want ev−1({p}× C)to consist of points.Hence we take C to be a line(which is of course a smooth submanifold)in Q∞which transversely intersects Mp,regarded as a subset in Q∞,in a point q0.We get a unique element in M(J0,[L])×Aut(CP1)CP1×CP1which maps to(p,q)∈ Qn×Qn,and we may represent this element by(u;[0:1],[1:0]).

To check that the evaluation map is transverse to{p}×C,we observe that C is transverse to the set

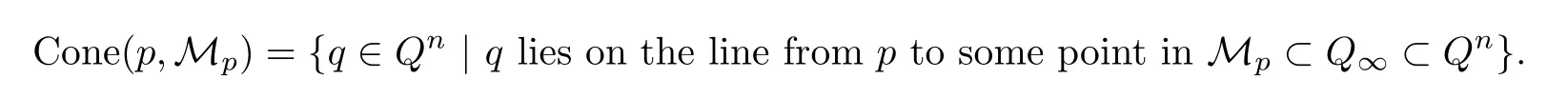
First we show that vectors of the form(v,0)∈TpQn×Tq0Qnlie in the image of T[u;[0:1],[1:0]]ev.Indeed,put ps:=expp(sv),and follow the above procedure to define Mps.For a small s,we find a unique intersection point qs:=Mps∩C.Therefore we find a variation(us,[0:1],[1:0])which maps to(ps,qs)under ev.Note here that the curve qsis tangent to C.

To see that a vector of the form(0,w)also lies in the image of T[u;[0:1],[1:0]]ev,we first note that we can assume that w lies in the tangent space to Cone(p,Mp)since the normal to Cone(p,Mp)is tangent to C.The curve:=expp(sw)lies in Cone(p,Mp),so by definition of this cone,we find a line from p to.Hence we find a variation(us,[0:1],[1:zs])which maps to(p,).

We conclude the following result.

Proposition 3.1The2-point Gromov-Witten invariant([p],[C])equals1.

We remind the reader that H2(Q2)Z ⊕ Z,and there are two distinct homology classes[L]represented by a line in this case.We collect the above results in the following theorem.

Theorem 3.1The projective quadricQnadmits a decoration byD=(Qn−1,[L],C),where[L]is the homology class of a line andCis the submanifold described above.

Remark 3.1It is clear that the projective quadric has many anti-symplectic involutions.For instance,we can compose conjugation with swapping coordinates.

4 Existence of Invariant Curves

Complex conjugation on CP1defines an anti-symplectic involution R0:CP1→CP1,namely

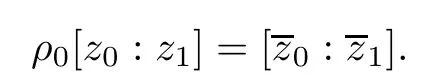
Now pick an ω-compatible almost-complex structure J on TM which is anti-invariant under ρ,so

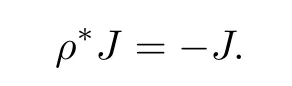
Denote the space of parametrized J-holomorphic maps from CP1to M by Hol(J).We define an involution on this space:

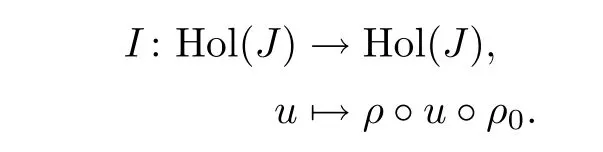
Now we will write the fixed-point locus of this involution as

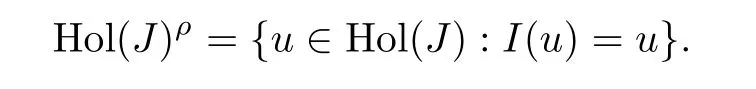
Take a point p∈M,a submanifold S⊂M and a spherical homology class A∈im(h),where h:π2(M)→ H2(M;Z)is the Hurewicz homomorphism,and define

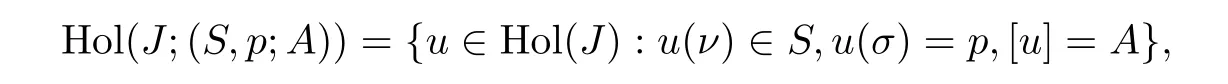
where ν =[1:0]∈ CP1is the “north-pole” and σ =[0:1]∈ CP1is the “south-pole”.Note that both the north-pole and the south-pole lie on the real part RP1=Fix(ρ0) ⊂ CP1.The parametrization has not yet been fully determined by just two marked points,so we still have a C∗-action on this space.Later,we will mod out by this action.

Suppose now that S is invariant under ρ,that the point p lies in the Lagrangian L=Fix(ρ),and that the homology class A is anti-invariant,so ρ∗A= −A.Then the space Hol(J,(S,p;A))is invariant under the involution I and we set

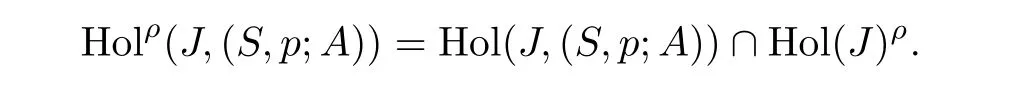
If Σ ⊂ M is a symplectic submanifold,we will write J(Σ,ρ)for the space of all ω-compatible almost-complex structures on M,which are anti-invariant under the anti-symplectic involution ρ and are restricted on Σ to an ω|Σ-compatible almost-complex structure such that Σ becomes a J-holomorphic submanifold of M.We will denote the complement of Σ in M by Σc.The main result of this section is the following theorem.

Theorem 4.1Assume that(M,ω,D,ρ)is a decorated real symplectic manifold with decorationD=(Σ,A,S).Then for every pointp∈ L∩Σcand every almost-complex structureJ ∈ J(Σ,ρ),the moduli space(S,p;A)=Holρ(J,(S,p;A))/C∗is nonempty.

The proof of Theorem 4.1 needs some preparation.We first recall from[13,Section2.5]that a holomorphic curve u:CP1→M is called multiply covered if there exists a holomorphic curve v:CP1→ M and a holomorphic map φ:CP1→ CP1satisfying

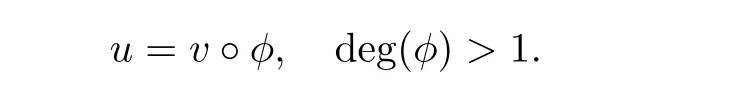
If a curve is not multiply covered,it is called simple.

Lemma 4.1A holomorphic curveu∈Hol(J)is simple if and only ifI(u)is simple.

ProofFirst suppose that u is simple and that v ∈ Hol(J)and φ:CP1→ CP1is a holomorphic map such that

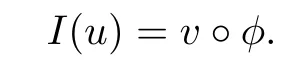
By using that I is an involution,we compute

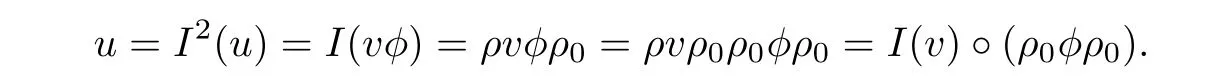
Since u is simple,by assumption,we conclude that

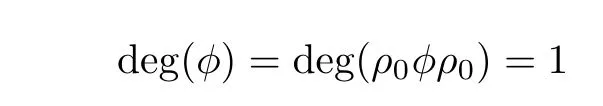
and therefore I(u)is simple as well.This proves the “only if” part and the “if”part follows again from the fact that I2(u)=u.

We now need the fact that Aut(CP1)=PSL2(C).

Definition 4.1A simple holomorphic curveu∈Hol(J)is called a pseudo- fixed point if there existsφ ∈ PSL2(C)such thatI(u)=u ◦φ.It is called a fixed point ifφis the identity,i.e.,I(u)=u.

Remark 4.1It follows from[13,Proposition 2.5.1]that a simple holomorphic curve has no nontrivial automorphisms.Therefore the map φ for a pseudo- fixed point is uniquely determined.

Lemma 4.2Assume thatu∈ Hol(J)is a pseudo- fixed point,so thatI(u)=uφfor someφ ∈ PSL2(C).Thenφρ0:CP1→ CP1is an anti-holomorphic involution.

ProofIt is clear that φρ0is anti-holomorphic.To check that it is an involution,we compute

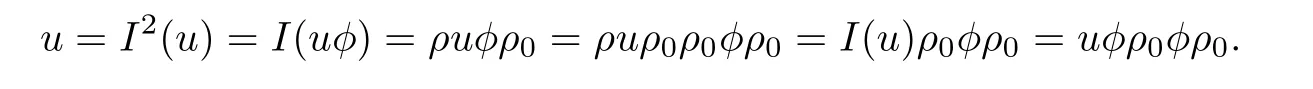
Since u is simple by assumption,it follows from[13,Proposition 2.5.1]that u has no nontrivial automorphisms so that

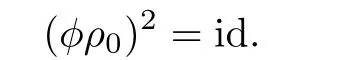
This finishes the proof of the lemma.

We abbreviate by I⊂Diff(CP1)the space of anti-holomorphic involutions of CP1.

Proposition 4.1The spaceIhas two connected components.

ProofWe first show that I is diffeomorphic to the space

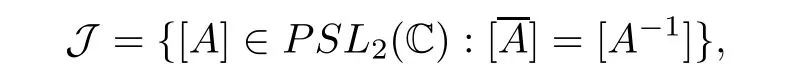
where for A∈SL2(C)we denote by[A]its equivalence class in the projectivization PSL2(C)and bythe complex conjugate of the matrix A.We define a map

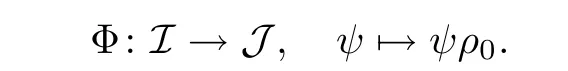
To check that this map is well defined,we first note that ψρ0:CP1→ CP1is a biholomorphism so that ψρ0=[A] ∈ PSL2(C).Now we compute by using the fact that ρ0as well as ψ are involutions

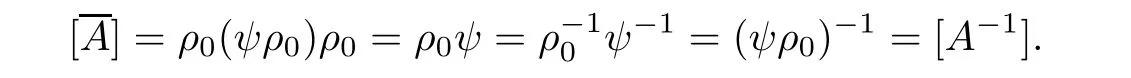
This proves that Φ is well defined.To show that it is a diffeomorphism we construct its inverse as follows

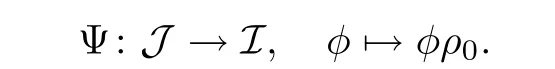
That Ψ is inverse to Φ is an immediate consequence of the fact that ρ0is an involution.Therefore it just remains to check that Ψ is well defined,i.e.,φρ0is actually an involution.This follows from the following computation:

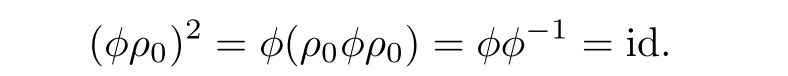
This proves that I and J are diffeomorphic.

In view of the diffeomorphism established above,we are left to show that J has two connected components.We rewrite J first as the quotient

where

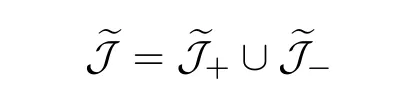
with

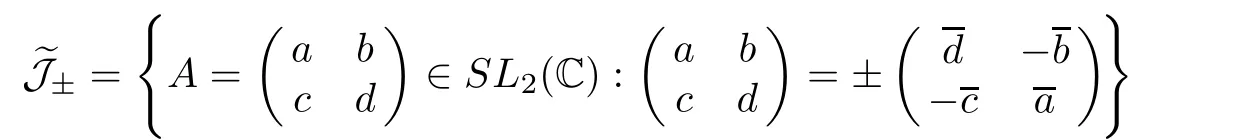
and the Z2-action identifies A with−A.Note that bothandare invariant under the Z2-action.Ifthen this is equivalent to that

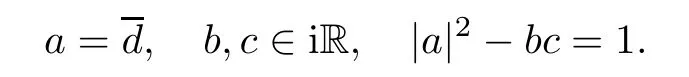
Hence we can identifywith the hyperboloid of one sheet

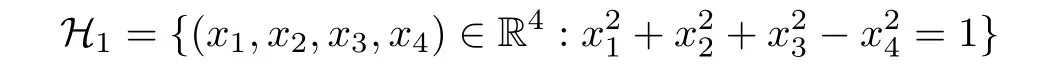
via the map

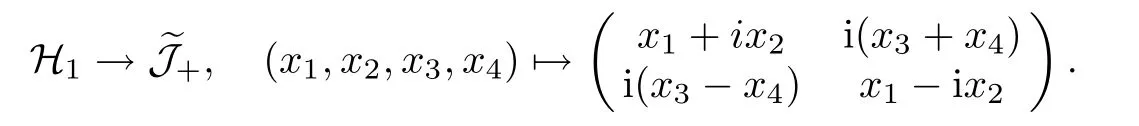
The hyperboloid of one sheet H1is connected and therefore we conclude thatandare connected as well.

It remains to show thatis connected as well.Ifthen this is equivalent to that

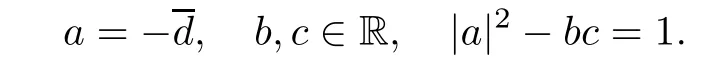
Hence we can identifywith the hyperboloid of two sheets

via the map

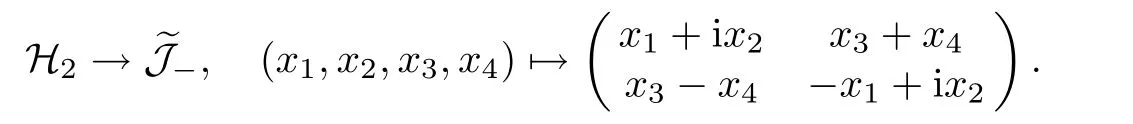
The pullback of the involution onto H2is given by x→ −x.This involution interchanges the two sheets of H2and thereforeis connected.This finishes the proof of the proposition.

Keeping the notation from the proof of Proposition 4.1,we abbreviate the two connected components of the space I by

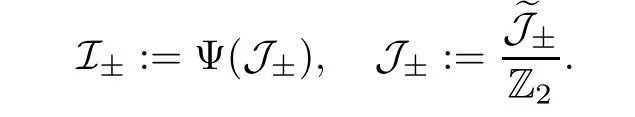
An example of a holomorphic involution in I+is the involution ρ0:[z0:z1]→ [z0:z1]and an example of an anti-holomorphic involution in I−is the antipodal map σ0:[z0:z1]→ [z1:−z0].Note that the fixed-point set of ρ0is topologically a circle,while σ0has no fixed points.Since the topological type of the fixed-point set only depends on the connected component of I,we conclude with the following lemma.

Lemma 4.3Each anti-holomorphic involution inI−acts freely,while the fixed-point set of each involution inI+is topologically a circle.

Definition 4.2A pseudo- fixed-pointu∈ Hol(J)satisfyingI(u)=uφis said to be of type I ifφ ∈ J+.Otherwiseuis said to be of type II,meaning thatφ ∈ J−.

Proposition 4.2Assume thatu∈Hol(J)is a pseudo- fixed-point of typeI.Then there existsψ∈PSL2(C)such thatu◦ψis a fixed point.

ProofSince u is a pseudo- fixed-point,we have I(u)=uφ for φ ∈ PSL2(C)and because u is of type I,we have φρ0∈ I+.By Lemma 4.3 we know that the fixed-point set of φρ0is topologically a circle.Identify CP1with the 2-dimensional sphere S2={x∈R3:?x1}via stereographic projection.We first claim that the fixed-point set Fix(φρ0)is actually a small circle,namely,the intersection of S2with an affine plane in R3.To see this,pick three points on Fix(φρ0).These three points uniquely determine a small circle.Since φ and ρ0map small circles to small circles,we conclude that this small circle is fixed under φρ0and hence has to agree with Fix(φρ0).This shows that Fix(φρ0)is a small circle.

Since the group PSL2(C)acts transitively on small circles,we conclude that there exists ψ∈PSL2(C)satisfying

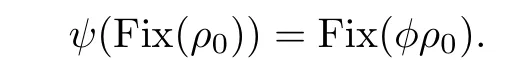
This implies that

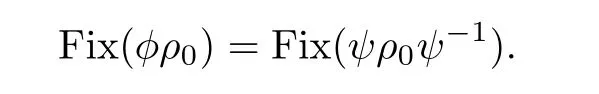
By analyticity,we conclude that

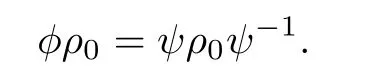
Using this equality,we compute

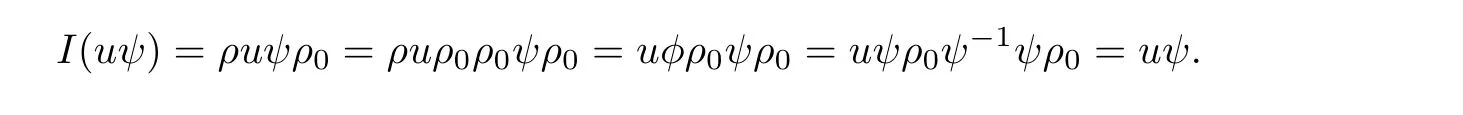
Hence uψ is a fixed point.This finishes the proof of the proposition.

Proposition 4.3Assume thatΣ ⊂ Mis a complexρ-invariant hypersurface andu ∈Hol(J)is a pseudo- fixed-point satisfying[u]◦ [Σ]=1andim(u)?⊂ Σ.Thenuis of typeI.

ProofSince[u]◦ [Σ]=1,the image of u is not contained in Σ and Σ is complex,we deduce from positivity of intersections that#u−1(Σ)=1,i.e.,there exists w0∈ CP1such that

Since u is a pseudo- fixed-point,there exists φ ∈ PSL2(C)such that I(u)=uφ.We compute by using the ρ-invariance of Σ,

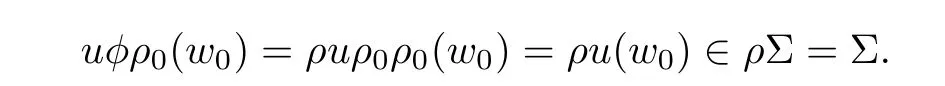
We deduce from(4.1)that

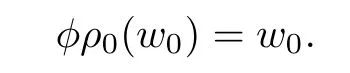
In particular,the fixed-point set of the anti-holomorphic involution φρ0is not empty.We conclude by Lemma 4.3 that φρ0∈ I+or equivalently that φ ∈ J+,and therefore u is a pseudo- fixed-point of type I.This proves the proposition.

Definition 4.3Assumeu ∈ Hol(J).A pointw ∈ CP1is called aρ-injective point ofuif

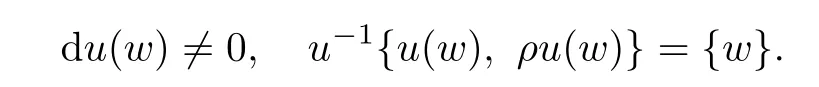
Lemma 4.4Assume thatu∈Hol(J)is a simple holomorphic map which is not a pseudofixed-point.Then the complement of the set ofρ-injective points ofuis finite.

ProofDenote by Zρ⊂ CP1the complement of the set of ρ-injective points.Abbreviate further

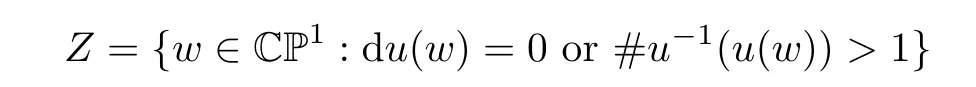
the set of non-injective points of u and

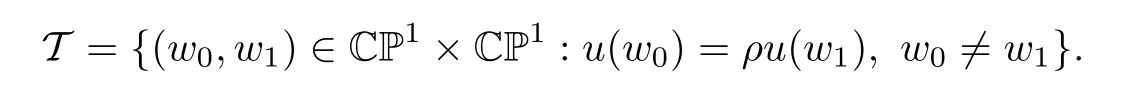
Consider the map

Note that

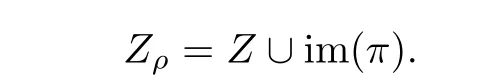
Since u is simple,the set Z is finite by positivity of intersection(see[13,Theorem E.1.2]).It therefore suffices to show that the set T is finite as well.To see that, first note that by Lemma 4.1,I(u)is simple as well.Therefore it follows from[13,Corollary 2.5.3]that

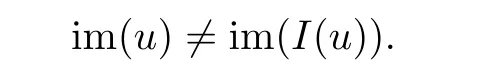
Hence by positivity of intersection

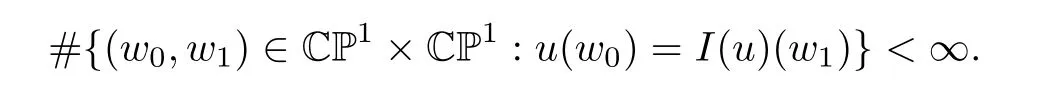
Note that

We deduce that

This finishes the proof of the lemma.

We are now ready to prove the main result of this section.

Proof of Theorem 4.1We argue by contradiction and assume that there exists J∈J(Σ,ρ)such that the moduli space(S,p;A)=is empty.Since A is indecomposable,there is no bubbling and therefore it follows from compactness of holomorphic curves that there exists an open neighborhood J0⊂ J(Σ,ρ)of J such that=∅for every J'∈J0.In view of Proposition 4.2,there is therefore no pseudo- fixed-point of type I in the space of holomorphic maps Holρ(J',(S,p;A))for every J' ∈ J0.Together with Proposition 4.3,the assumptions of the theorem show that there does not exist a pseudo- fixed-point of type II either and therefore there are no pseudo- fixed-points at all in Hol(J',(S,p;A))for every J'∈J0.

Furthermore,A is indecomposable,so each holomorphic curve u representing A is simple and we conclude by Lemma 4.4 that for every J'∈J0,every holomorphic map u∈Hol(J',(S,p;A))has ρ-injective points.Transversality arguments(see[13,Section 6.2,Section 6.3]),then show that there exists an open and dense subset⊂J0such that for every J'∈the Gromov-Witten invariant GWA([S],[p])can be obtained as the signed count of points in the moduli space M(J',(S,p;A))=Hol(J',(S,p;A))/C∗.Since this Gromov-Witten invariant is odd by assumption,we conclude that

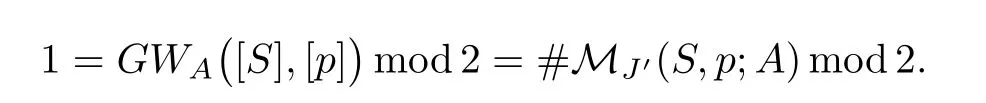
However,the moduli space MJ?(S,p;A)is invariant under the involution I which has no fixed points by construction.Therefore the cardinality of the moduli space MJ?(S,p;A)has to be even.This contradiction finishes the proof of the theorem.

5 The Proof

The basic idea to prove Theorem 1.2 is to embed a real Liouville domain into a decorated symplectic manifold,making it into a Christmas tree.By hanging up some Christmas balls,or in other words,taking holomorphic spheres through Σ and a given real point p,and applying a stretching construction,we obtain an invariant finite energy plane through a given point in the real locus.

We need some lemmas to prepare the Christmas tree for the Christmas balls.

Lemma 5.1Let(M,ω,D=(Σ,A,S))be a decorated symplectic manifold with an antisymplectic involutionρ,and assume that(W0,λ0,ρ|W0)is a real Liouville domain that embeds into the interior ofM −ν(Σ)for someρ-invariant neighborhoodν(Σ)ofΣ.Suppose in addition thatb1(W0)=0.

ThenW1:=M − ν(Σ)carries the structure of a real Liouville domain(W1,λ1,ρ|W1)such that(W0,λ0,ρ|W0)is a real Liouville subdomain in the sense thatλ1|W0= λ0.

ProofSince we will need a cut-o fffunction,we first extend λ0to a neighborhood of W0.By Lemma 3.1,W1:=M−ν(Σ)is a real Liouville domain(W1,,ρ).As ω==dλ0on a neighborhood of W0,we see that−λ0is closed,and as b1(W)=0,we find a function f on a neighborhood of W0such that λ0=−df.It follows directly that ρ∗df= −df.If ρ∗f−f,then we replace f by

Find a ρ-invariant cut-o fffunction g such that g ≡ 1 on W0,and g ≡ 0 on the complement of a neighborhood of W0.Then λ1=−d(gf)has the desired properties.

Lemma 5.2Let(M,ω,D=(Σ,A,S))be a decorated symplectic manifold,and assume that(W0,λ0,ρ|W0)is a real Liouville domain that embeds into the interior ofM − ν(Σ)for someρ-invariant neighborhoodν(Σ)ofΣ.Suppose in addition thatb1(W0)=0.LetJbe an almost-complex structure onMthat is compatible withωand SFT-like near∂W0.

Assume thatu:CP1→Mis aJ-holomorphic sphere through a pointp∈W0such that[u]◦ [Σ]=1.Then the componentCofu−1(W0)containingz0withu(z0)=psatisfies the following:

(1)Cis diffeomorphic to a disk.

(2).In particular,the SFT energy ofu|Cis bounded from aboveby1.

ProofAfter possibly shifting the boundary ∂W0a little bit,we can assume that u−1(∂W0)consists of finitely many circles.Let C denote the component of u−1(W0)containing z0.We claim that C has only one boundary component.To see why,note that if C has more than one boundary component,then there is a connected component of?C:=CP1−int(C)with the properties

(1)shares a boundary component with C.

(2)does not intersect ν(Σ),and is contained in M − int(W0).

To see that,the latter condition can be imposed.We observe that u intersects Σ only once,and we also use that CP1has genus 0.

Now apply the previous lemma to see that M − ν(Σ)carries the structure of a real Liouville domain(W1,λ1)with a real Liouville subdomain(W,λ).This allows us to compute the energy of?C via Stokes’theorem,

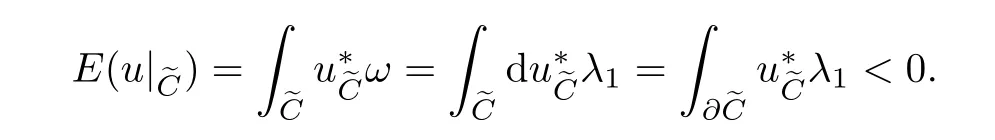
The last inequality holds,because the orientation induced by the outward pointing normal is minus the one induced by the Reeb vector field;one can see this by using that J is SFT-like near∂W0.Since the energy of the holomorphic curveis positive,this is a contradiction,so we conclude that C has one boundary component.It follows directly that C is diffeomorphic to a disk.The claimed energy estimate is now also clear,since?CP1u∗ω =1.

We will now apply a stretching argument to obtain an invariant finite energy plane.This is illustrated in Figure 1.Let X denote the Liouville vector field on M−Σ.Take a point p∈W0,

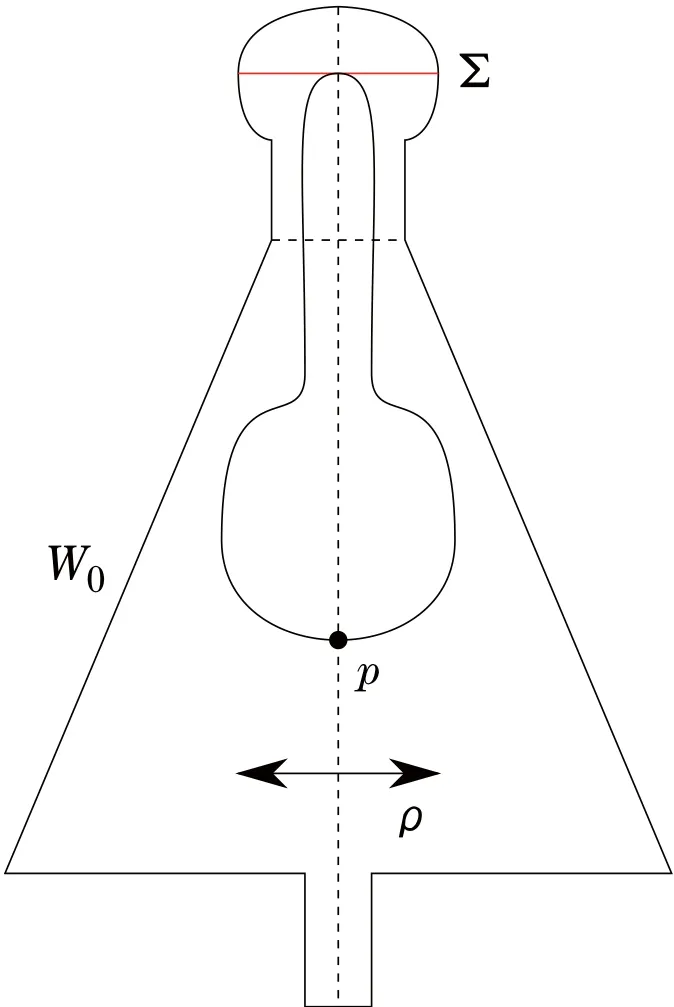
Figure 1 Hanging up Christmas balls(holomorphic spheres)in a Christmas tree

and for τ∈R≥0define pτ,by following the Liouville flow backwards,as pτ=Define the stretched Liouville domainby

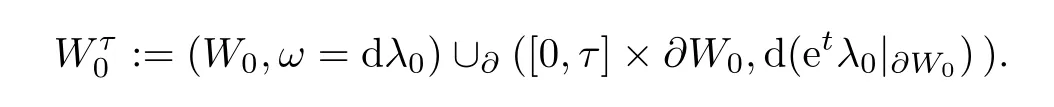
Choose a compatible complex structure Jτon,which is SFT-like on[0,τ]×∂W0.We choose this sequence Jτsuch that it is a constant sequence of complex structures when restricted to W0.Since the map x→(x)provides a symplectic deformation from W0to Wτ0,we can pull back Jτto a complex structure on W0,which is SFT-like near the boundary.Extend this Jτto a compatible complex structurefor(M,ω).

With Lemma 5.2 applied to an invariant holomorphic sphere obtained with Theorem 4.1,we find a-holomorphic disk

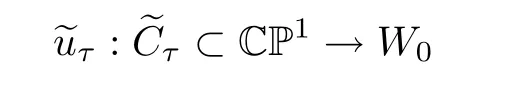
going through pτ,with its boundary on ∂W0.We now stretch the Liouville domain W0to a Liouville domainby using the above deformation.This deformation also gives us a Jτ-holomorphic curve

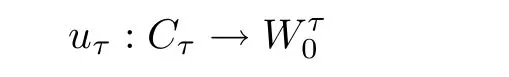
going through p.As the Hofer energy of?uτis bounded by 1,so is the Hofer energy of uτ.

Denote the norm induced by ωτ(·,Jτ·)by? ·?τ.By rescaling the domain,we can ensure thatwe need to rescale the disk Cτfor this,but we will continue to write Cτfor this rescaled disk.Since p lies in W0and the boundary of the disk,uτ(∂Cτ),lies on{τ}× ∂W0,we see directly that the radius for the disk Cτhas to be at least τ by a very crude estimate,usingTaking the limit τ→ ∞,we find a convergent subspace,and obtain a map

whereis the completion of W0.As the Hofer energy of u∞is bounded from above by 1,we conclude that u∞is the desired finite energy plane through p∈W0.

This stretching construction also implies the well-known corollary(see also[11]).

Corollary 5.1Let(W,λ)be a Liouville domain admitting an embedding into a decorated symplectic manifold(M,ω,D).Suppose thatb1(W)=0.ThenWis uniruled.Furthermore,there exists a periodic orbit of a period less than or equal to1for the Reeb flow on∂W.

AcknowledgementsWe thank Jungsoo Kang for the helpfulcomments.The second author also holds a joint appointment in the Research Institute of Mathematics,Seoul National University.

[1]Albers,P.,Frauenfelder,U.,van Koert,O.and Paternain,G.,The contact geometry of the restricted 3-body problem,Comm.Pure Appl.Math.,65(2),2012,229–263.

[2]Birkho ff,G.,The restricted problem of three bodies,Rend.Circ.Matem.Palermo,39,1915,265–334.

[3]Georgieva,P.and Zinger,A.,Enumeration of real curves in CP2n−1and a WDVV relation for real Gromov-Witten invariants,arXiv:1309.4079.

[4]Hofer,H.and Viterbo,C.,The Weinstein conjecture in the presence of holomorphic spheres,Comm.Pure Appl.Math.,45(5),1992,583–622.

[5]Hofer,H.,Wysocki,K.and Zehnder,E.,Properties of pseudoholomorphic curves in symplectisations I:Asymptotics,Ann.Inst.Henri Poincar´e,13,1996,337–379.

[6]Hofer,H.,Wysocki,K.and Zehnder,E.,Properties of pseudoholomorphic curves in symplectisations IV:Asymptotics with degeneracies,in Contact and Symplectic Geometry,Thomas,C.B.,e.d.,Cambridge University Press,Cambridge,1996,78–117.

[7]Hofer,H.,Wysocki,K.and Zehnder,E.,Correction to“Properties of pseudoholomorphic curves in symplectisations I:Asymptotics”,Ann.Inst.Henri Poincar´e,15–4,1998,535–538.

[8]Hu,J.,Li,T.J.and Ruan,Y.,Birational cobordism invariance of uniruled symplectic manifolds,Invent.Math.,172(2),2008,231–275.

[9]Li,T.J.,Existence of Symplectic Surfaces,Geometry and Topology of Manifolds,Fields Inst.Commun.,Vol.47,Amer.Math.Soc.,Providence,RI,2005,203–217.

[10]Liu,G.and Tian,G.,Weinstein conjecture and GW-invariants,Comm.Contemp.Math.,2(4),2000,405–459.

[11]Lu,G.,The Weinstein conjecture in the uniruled manifolds,Math.Res.Lett.,7(4),2000,383–387.

[12]McDu ff,D.and Salamon,D.,Introduction to Symplectic Topology,Second edition.Oxford Mathematical Monographs,The Clarendon Press,Oxford University Press,New York,1998.

[13]McDu ff,D.and Salamon,D.,J-holomorphic Curves and Symplectic Topology,American Mathematical Society Colloquium Publications,Vol.52,American Mathematical Society,Providence,RI,2004.

[14]McLean,M.,Symplectic invariance of uniruled affine varieties and log Kodaira dimension,Duke Math.J.,163(10),2014,1929–1964.

[15]Milnor,J.and Stashe ff,J.,Characteristic classes,Annals of Mathematics Studies,Vol.76,Princeton University Press,Princeton,N.J.,University of Tokyo Press,Tokyo,1974.

[16]Mora,E.,Pseudoholomorphic cylinders in symplectisations,Doctoral dissertation,New York University,2003.

[17]Okonek,C.,Schneider,M.and Spindler,H.,Vector Bundles on Complex Projective Spaces,Birkhäuser,Springer Basel AG,Basel,2011.

[18]Pandharipande,R.and Thomas,R.,ways of counting curves,Proceedings of“School on Moduli Spaces”,Isaac Newton Institute,Cambridge,2011,arXiv:1111.1552.

[19]Seifert,H.,Periodische Bewegungen mechanischer Systeme,Math.Z.,51,1948,197–216.

[20]Welschinger,J-Y.,Invariants of real symplectic 4-manifolds and lower bounds in real enumerative geometry,Invent.Math.,162(1),2005,195–234.

[21]Wendl,C.,Contact hypersurfaces in uniruled symplectic manifolds always separate,J.Lond.Math.Soc.,89(2),2014,832–852.