Sharp Distortion Theorems for a Subclass of Biholomorphic Mappings Which Have a Parametric Representation in Several Complex Variables∗

Xiaosong LIUTaishun LIU

1 Introduction

In the case of one complex variable,it is well known that any univalent function has a parametric representation.However,Poreda[1],Kohr[2]and Graham,Hamada and Kohr[3]all pointed out that there are differences between one complex variable and several complex variables.

For the case of several complex variables,Poreda[1] first discussed biholomorphic mappings of the unit polydisk in Cnwhich have a parametric representation.After that,Kuba and Poreda[4]studied the parametric representation of starlike mappings defined on the Euclidean unit ball in Cn.Further results in the case of the Euclidean unit ball were obtained by Kohr[2].The case of a unit ball with any arbitrary norm in Cnis due to Graham,Hamada and Kohr[3].Kohr and Liczberski[5]extended the above results to the general case.On the other hand,some of the above results were extended to the case of bounded complete circular domains whose Minkowski functional is C1on Cn{0}.As to the case of the unit ball in Banach spaces,Hamada,Honda and Kohr[6]and Hamada and Honda[7]derived general versions of the prior results.Recently,Xu and Liu[8]and Xu,Liu and Xu[9]discussed the distortion theorems of a subclass of biholomorphic mappings which have a parametric representation from different aspects,respectively.We also mention that the definition of the biholomorphic mappings with a parametric representation in[8]is slightly different to that in[6],and their proofs were given without applying the Loewner chain.

Up to now,there have been a lot of signi ficant results which cope with the distortion theorems for convex mappings.For instance,Barnard,FitzGerald and Gong[10] first established the estimates of the Jacobi-determinant type for convex mappings defined on the Euclidean unit ball in C2in 1994,and after that,Liu and Zhang[11]extended the above result to the general case.With respect to the distortion theorem of the Fr´echet-derivative type for convex mappings,the related results for convex mappings were first studied by Gong,Wang and Yu[12].Consequently,many distinct versions of the distortion theorem for convex mappings on different unit balls in complex Banach spaces were discussed by Gong and Liu[13],Liu and Zhang[14],Zhu and Liu[15],as well as Chu,Hamada,Honda and Kohr[16].In particular,a strong version of the upper bounds estimate of the distortion theorem for convex mappings on the unit ball of a complex Hilbert space was obtained,due to Hamada and Kohr[17].However,compared with the distortion theorems for convex mappings,there are only the following two results directly concerning the distortion theorem for starlike mappings by now.One is the distortion theorem for starlike mappings on the unit polydisk along a unit direction which was derived by Liu,Wang and Lu[18],the another is the sharp distortion theorem for a subclass of starlike mappings in several complex variables,due to Liu and Liu[19].

Let X denote a complex Banach space with the norm?·?,X∗be the dual space of X,B be the open unit ball in X,and U be the Euclidean open unit disk in C.Also,let Unbe the open unit polydisk in Cn,and N be the set of all positive integers.Let∂Undenote the boundary of Un,∂0Unbe the distinguished boundary of Un.Let the symbol'mean the transpose.For each x∈X{0},we define

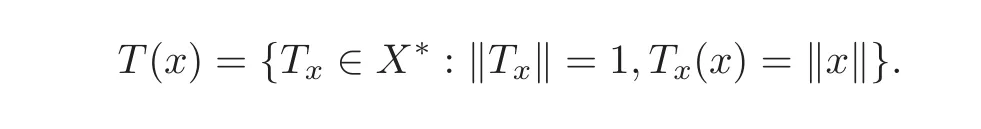
By the Hahn-Banach theorem,T(x)is nonempty.

Let H(B)be the set of all holomorphic mappings from B into X.We know that if f∈H(B),then

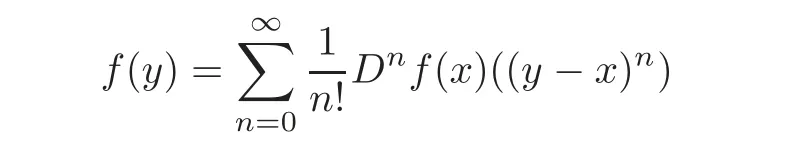
for all y in some neighborhood of x ∈ B,where Dnf(x)is the nth-Fr´echet derivative of f at x,and for n≥1,

Furthermore,Dnf(x)is a bounded symmetric n-linear mapping fromX into X.

We say that a holomorphic mapping f:B → X is biholomorphic if the inverse f−1exists and is holomorphic on the open set f(B).A mapping f∈H(B)is said to be locally biholomorphic if the Fr´echet derivative Df(x)has a bounded inverse for each x ∈ B.If f:B → X is a holomorphic mapping,then we say that f is normalized if f(0)=0 and Df(0)=I,where I represents the identity operator from X into X.

We say that a normalized biholomorphic mapping f:B→X is a starlike mapping if f(B)is a starlike domain with respect to the origin.

Now we recall some definitions as follows.

Definition 1.1(cf.[8])Suppose thatg∈H(U)is a biholomorphic function such that(so,ghas real coefficients in its power seriesexpansion),and assume thatgsatisfies the conditions:

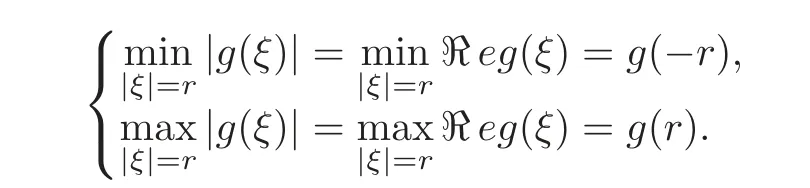
We denote by Mgthe set

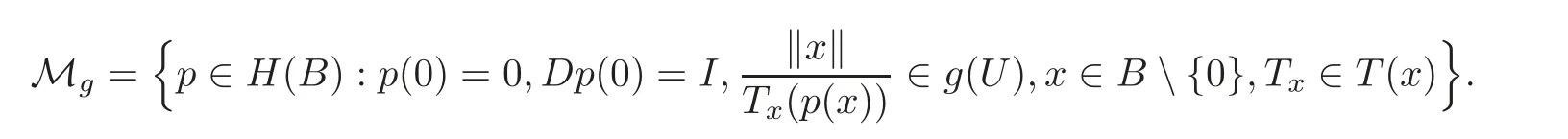
Definition 1.2(cf.[20])Suppose thatf:B→Xis a normalized locally biholomorphic mapping.Ifα∈(0,1)and

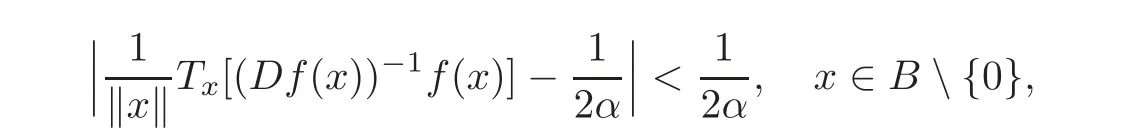
then we say thatfis a starlike mapping of orderαonB.

We denote bythe set of all starlike mappings of order α on B.

Definition 1.3(cf.[21])Suppose thatf:B→Xis a normalized locally biholomorphic mapping.Ifα∈(0,1]and

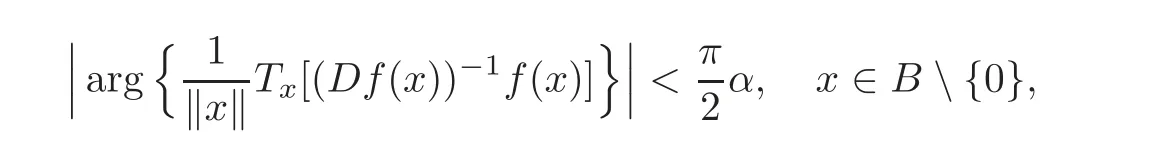
then we say thatfis a strongly starlike mapping of orderαonB.

Definition 1.3 in the case of the Euclidean unit ball Bnwas originally introduced by Curt[22].

Letbe the set of all strongly starlike mappings of order α on B.

Definition 1.4(cf.[23])Suppose thatf:B→Xis a normalized locally biholomorphic mapping.Ifα∈[0,1)and

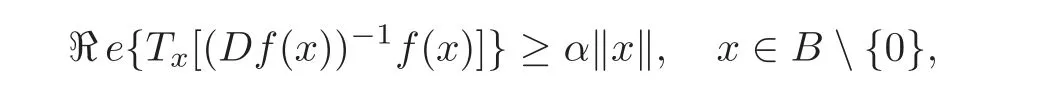
then we say thatfis an almost starlike mapping of orderαonB.

We denote bythe set of all almost starlike mappings of order α on B.

Definition 1.5(cf.[21])Suppose thatf:B→Xis a normalized locally biholomorphic mapping.Ifc∈(0,1)and

then we say thatfis a strongly starlike mapping onB.

Definition 1.5 in the case of the Euclidean unit ball Bnwas first introduced by Chuaqui[24].

Let SS∗(B)be the set of all strongly starlike mappings on B.

Definition 1.6(cf.[25])Letf∈H(B).It is said thatfisk-fold symmetric if

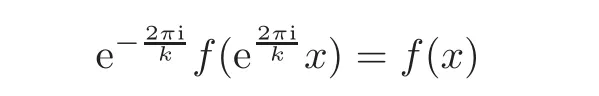
for allx∈B,wherek∈Nand

Definition 1.7(cf.[26])Suppose thatΩis a domain(a connected open set)inXwhich contains0.It is said thatx=0is a zero of orderkoff(x)iff(0)=0,···,Dk−1f(0)=0,butDkf(0)0,wherek∈N.

We readily see that x=0 is a zero of order k+1(k∈N)of f(x)−x if f is a k-fold symmetric normalized holomorphic mapping(f(x)?≡x)defined on B,but the converse fails.

Let(B)be the subset of S∗(B)consisting of normalized locally biholomorphic mappings f which satisfy(Df(x))−1f(x)∈ Mg,and let(B)be a subset of(B)such that x=0 is a zero of order k+1 of f(x)−x.We denote by(B)(resp.(B),(B),(B),(B))the subset of S∗(B)(resp.(B),(B),(B),SS∗(B))which satisfies that x=0 is a zero of order k+1 of f(x)−x.

In this paper,we organize the contents as follows.In Section 2,we shall establish the sharp distortion theorems of the Fr´echet-derivative type for a subclass of biholomorphic mappings which have a parametric representation on the unit ball of complex Banach spaces and the corresponding results of the above generalized mappings on the unit polydisk in Cn.In Section 3,we shall establish the sharp distortion theorems of the Jacobi-determinant type for a subclass of biholomorphic mappings which have a parametric representation on the unit ball with an arbitrary norm in Cnand the corresponding results of the above generalized mappings on the unit polydisk in Cnas well.Our derived conclusions are generalizations of some known results in the prior literatures.

2 Sharp Distortion Theorems of the Fr´echet-Derivative Type for a Subclass of Biholomorphic Mappings Which Have a Parametric Representation

In order to prove the desired theorems in this section,the following lemmas are necessary.

Lemma 2.1Ifh∈Mgandx=0is a zero of orderk+1ofh(x)−x,then

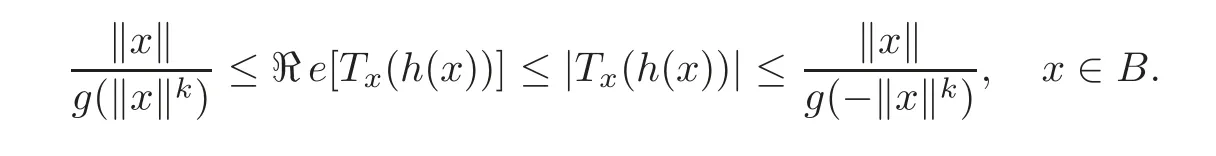
ProofFix x∈B{0},and we write x0=.Consider

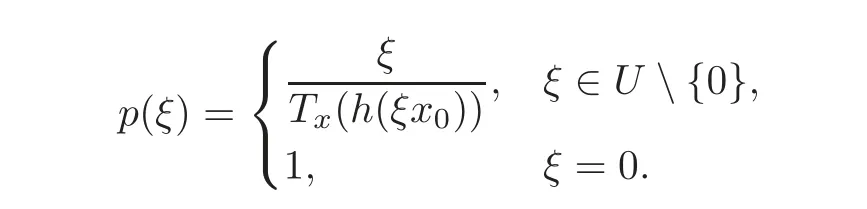
Then p∈H(U),p(0)=g(0)=1,and it is shown that

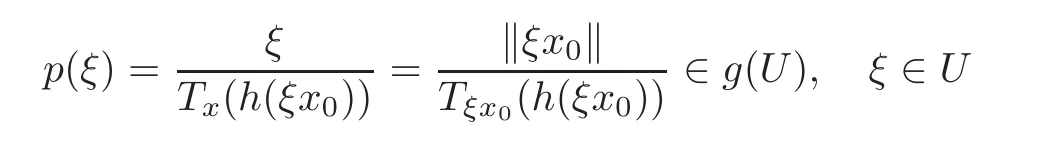
from h ∈ Mg.Also,since x=0 is a zero of order k+1 of h(x)− x,then ξ=0 is at least a zero of order k of ϕ(ξ) − 1,where ϕ(ξ)=.Let

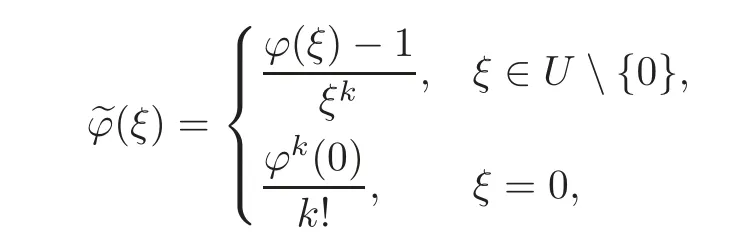
and then ϕ∈H(U).Note that

where ψ(ξ)=.In view of ψ−1(1)=0,

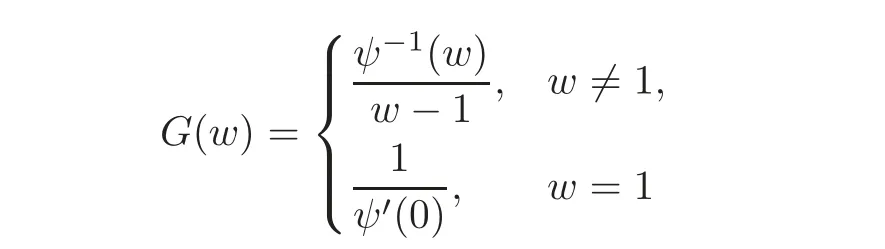
is well defined,and G is a holomorphic function in C.Hence

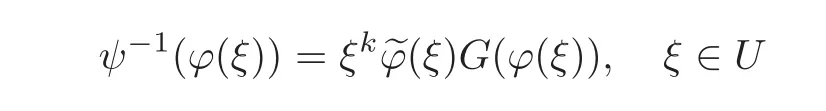
and

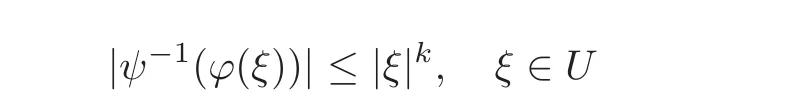
from the Schwarz lemma and(2.1).Therefore,

where H(ξ)= ϕ(ξ)G(ϕ(ξ)).Finally,taking into account the minimum principle of harmonic functions and the maximum modulus principle of holomorphic functions,it yields that

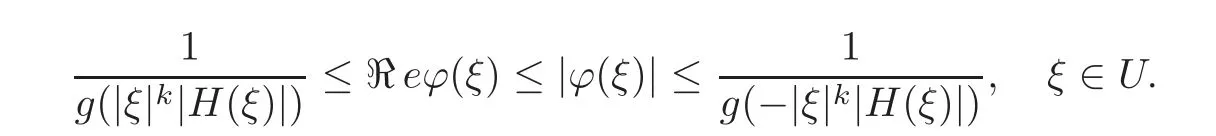
We mention thatis a decreasing function(resp.an increasing function)on the interval[0,1]from the maximum and minimum modulus principles of holomorphic functions.Thus

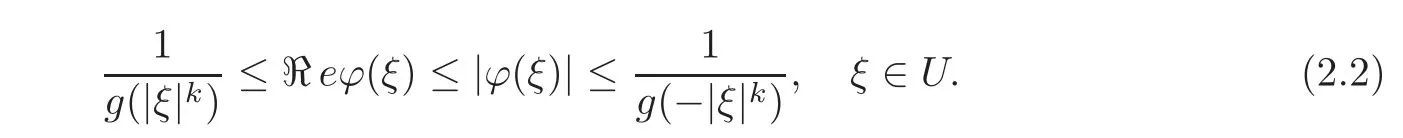
Taking ξ=?x?in(2.2),the result follows,as desired.This completes the proof.

Remark 2.1Lemma 2.1 provides more details of the proof than those in[9,Lemma 2.4],and our proof does not apply the subordinate principle.

Lemma 2.2(cf.[9,Theorem 2.1])If(B),then

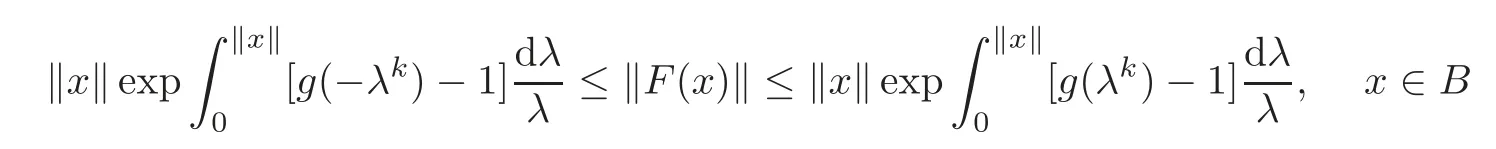
and the above estimates are sharp.

We now begin to present the following distortion theorems in this section.

Theorem 2.1Letg:U→Csatisfy the condition of Definition1.1,f:B→C∈H(B),andF(x)=xf(x)∈S∗g,k+1(B).Then

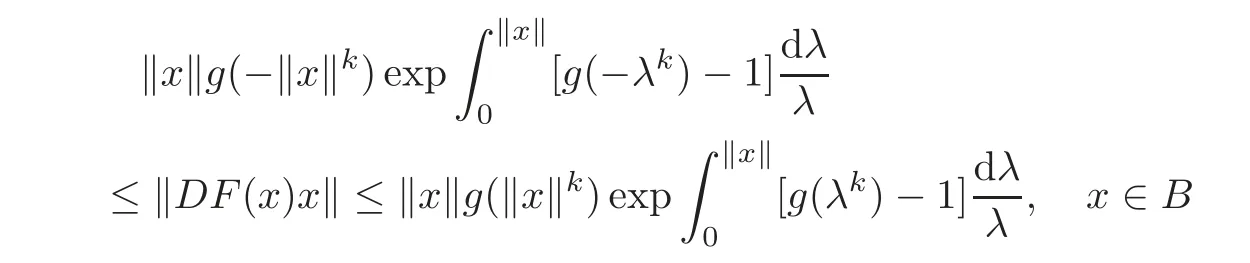
and the above estimates are sharp.

ProofIn view of F(x)=xf(x),it is shown that

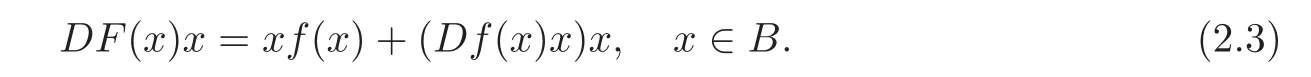
Also F(x)=xf(x)(B),and then it yields that

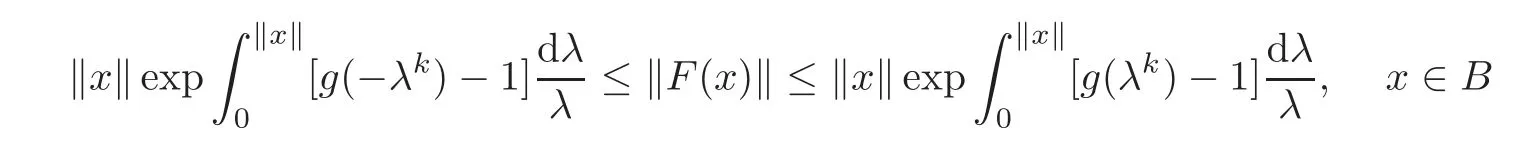
from Lemma 2.2.Hence

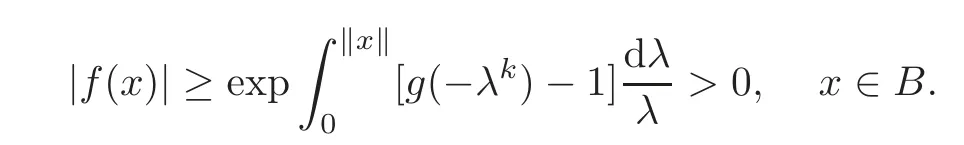
Namely,for x∈B.

It is shown that

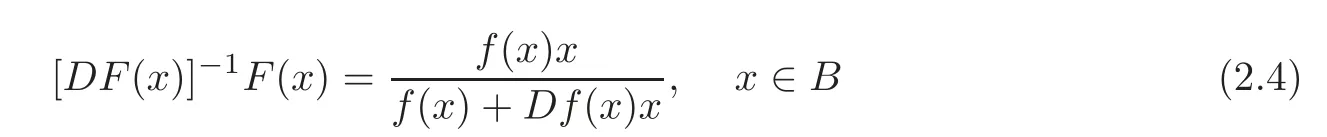
by a direct calculation.We mention thatif F ∈Consequently,by(2.4),we see that

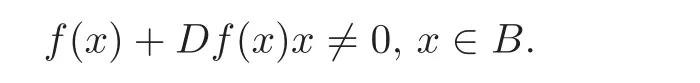
According to Lemma 2.1,it is shown that

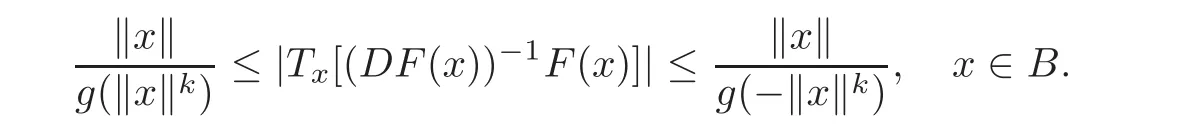
On the other hand,it yields that

from(2.3)–(2.4).Therefore the desired result follows from Lemmas 2.1–2.2.

Let b∈(U)such that b(0)=b'(0)−1=0 and

We define

where ϕ(ξ)=,and k=1,2,···.The branches of the above functions are chosen,which satisfy

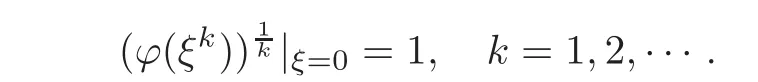
Also,consider

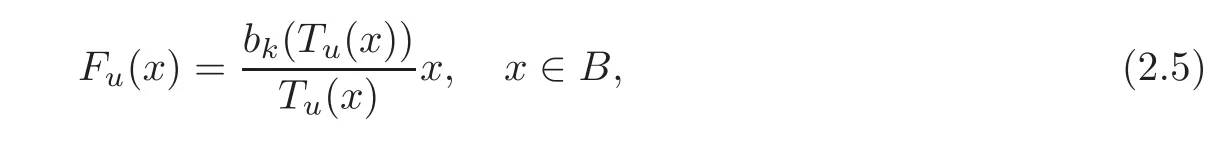
whereWe derive the following equivalent formulation of Theorem 2.1:

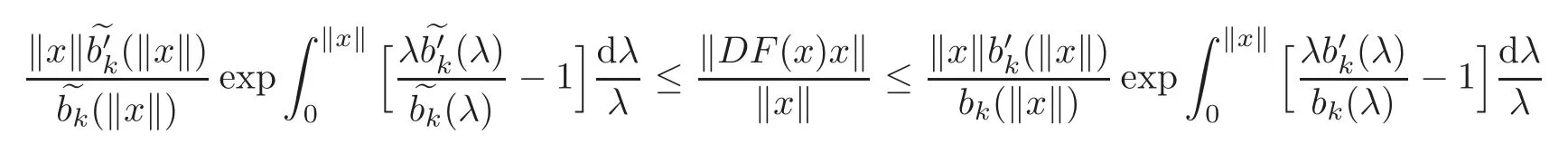
forwhereNote thatandThen it is shown that

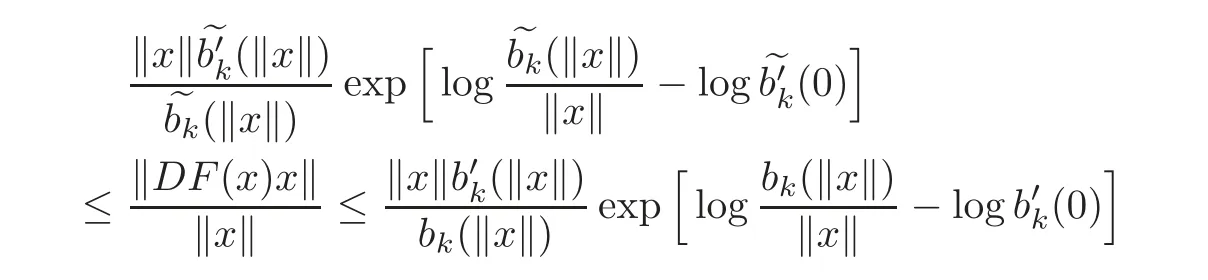
forThis implies that

Let Fu∈(B)be given by(2.5).A straightforward computation shows that?DFu(ru)ru?Then it is shown that the estimates of Theorem 2.1 are sharp.This completes the proof.

Remark 2.2Taking k=1 in Theorems 2.1,it is easy to see that Theorems 2.1 generalizes[8,Theorem 5].

Let g(ξ)=in Theorem 2.1.Then we derive the following corollary.

Corollary 2.1Letf:B→C∈H(B),andThen

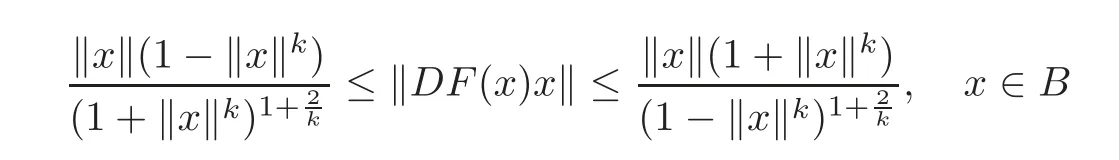
and the above estimates are sharp.

Let g(ξ)=in Theorem 2.1,where α ∈ (0,1).Then we get the following corollary.

Corollary 2.2Letf:B→C∈H(B),α∈(0,1),andF(x)=xf(x)∈(B).Then

and the above estimates are sharp.

Let g(ξ)=in Theorem 2.1,where α ∈ (0,1].Then we obtain the following corollary.

Corollary 2.3Letf:B→C∈H(B),α∈(0,1],andF(x)=xf(x)∈(B).Then

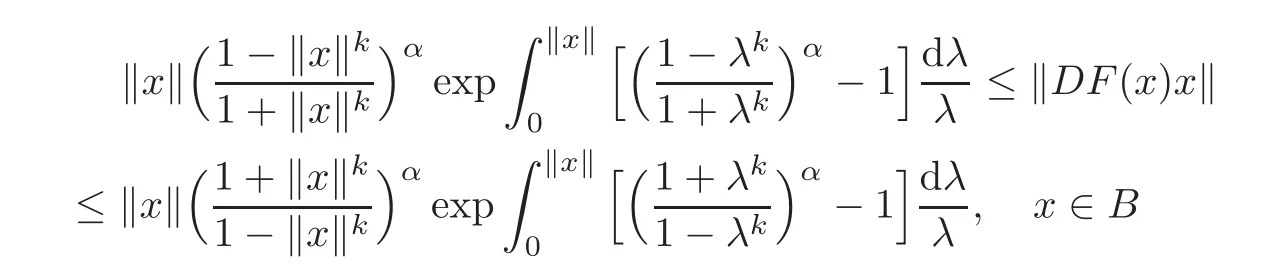
and the above estimates are sharp.

Let g(ξ)=in Theorem 2.1,where α ∈ [0,1).Then we derive the following corollary.

Corollary 2.4Letf:B→C∈H(B),andF(x)=xf(x)∈(B).

(i)Ifα ∈ [0,1)and,then

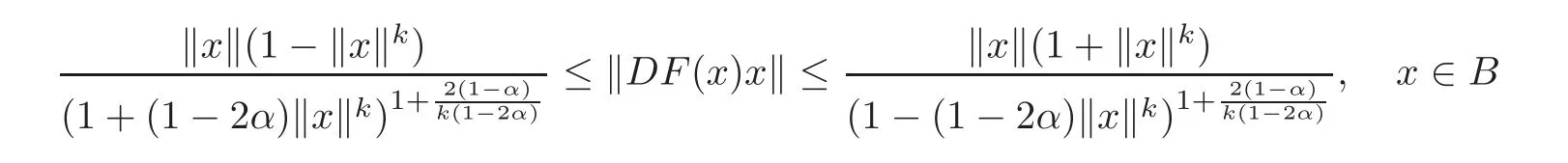
and the above estimates are sharp.

(ii)Ifα=then

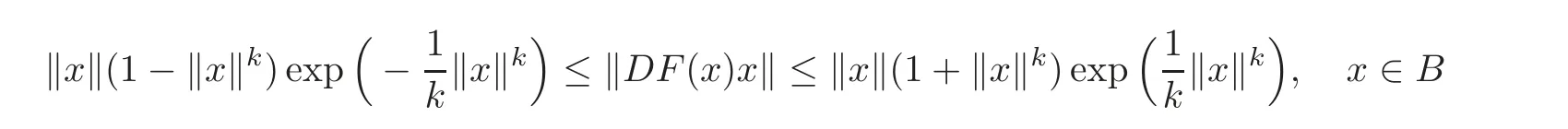
and the above estimates are sharp.

Let g(ξ)=in Theorem 2.1,where c ∈ (0,1).Then we get the following corollary.

Corollary 2.5Letf:B→C∈H(B),c∈(0,1),andF(x)=xf(x)∈(B).Then

and the above estimates are sharp.

In the following Theorem 2.2 and Corollaries 2.6–2.10,each mlis a non-negative integer,N=m1+m2+ ···+mn∈ N,ml=0 means that the corresponding components in Z=(Z1,···,Zl,···,Zn)'and F(Z)=(F1(Z1),···,Fl(Zl),···,Fn(Zn))'are vanished.

Theorem 2.2Letg:U→Csatisfy the condition of Definition1.1,fl:Uml→C∈H(Uml),l=1,2,···,n,andThen

forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

ProofLet F(Z)=(F1(Z1),F2(Z2),···,Fn(Zn))'.In view of the hypothesis of Theorem 2.2,for any Z=(Z1,Z2,···,Zn)'∈ UN,we see that

by a direct calculation.We mention that

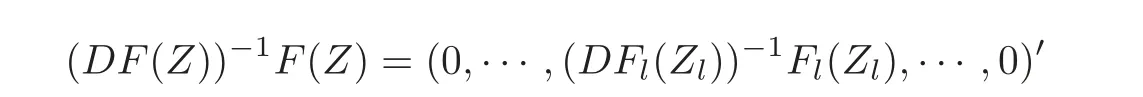
if Z=(0,···,Zl,···,0)'∈ Un,l=1,2,···,n.Let

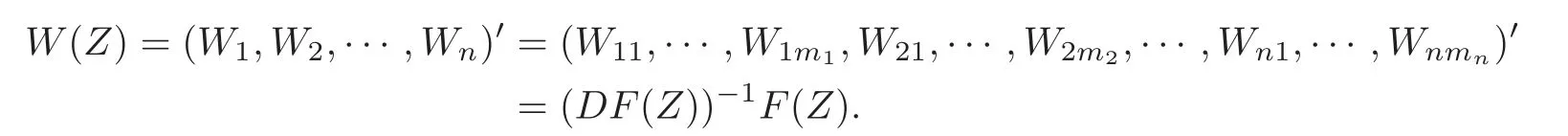
Then it is shown that

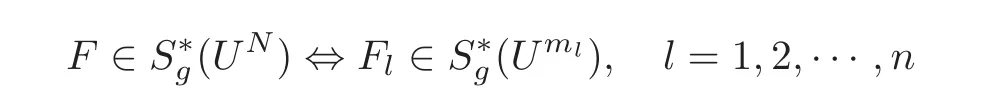
from the definition of S∗g(Un).Also we readily see that Zl=0 is at least a zero of order k+1 of each Fl(Zl)− Zl(l=1,2,···,n)if Z=0 is a zero of order k+1 of F(Z)− Z.In view of the fact that g(λk)>1 for λ >0,it is not difficult to know that tg(tk)is an increasing function on the interval[0,1)with respect to t.Noticing thatand

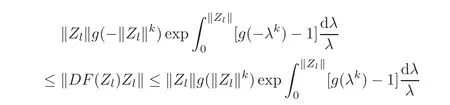
for Zl∈ Uml,l=1,2,···,n(the case B=Umlof Theorem 2.1),it is shown that

whereis brie fly denoted byand j satisfiesThe sharpness of the estimates of Theorem 2.2 is analogous to that in the proof of Theorem 2.1,so we only point out that the two equalities of the estimates of Theorem 2.2 hold for Zl=(eπikr,0,···,0)'(0 ≤ r<1)(l=1,2,···,n)and Zl=(r,0,···,0)'(0 ≤ r<1)(l=1,2,···,n),whereWe omit the details here.This completes the proof.

Lettingin Theorem 2.2,we get the following corollary.

Corollary 2.6Letg:U→Csatisfy the condition of Definition1.1,fl:Uml→C∈H(Uml),l=1,2,···,n,andFThen

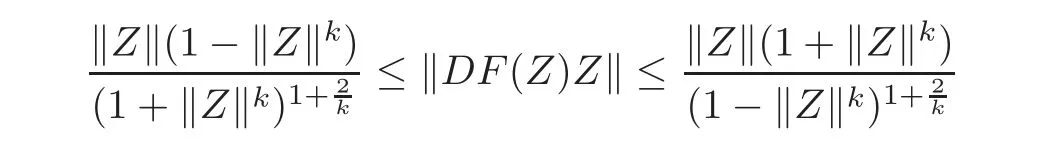
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Lettingin Theorem 2.2,where α ∈ (0,1),we derive the following corollary.

Corollary 2.7Letg:U→Csatisfy the condition of Definition1.1,α∈(0,1),fl:Uml→C∈H(Uml),l=1,2,···,n,andThen

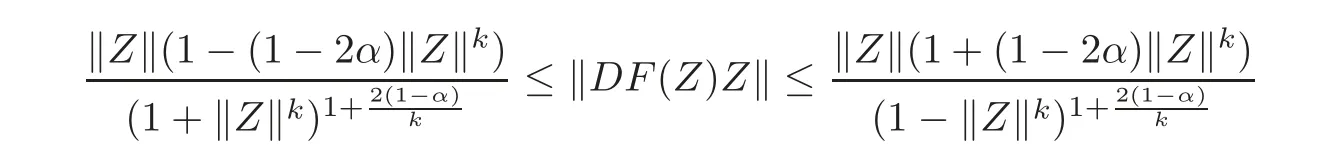
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Lettingin Theorem 2.2,where α ∈ (0,1],we obtain the following corollary.

Corollary 2.8Letg:U→Csatisfy the condition of Definition1.1,α∈(0,1],fl:Uml→ C ∈ H(Uml),l=1,2,···,n,andF(Z)=(Z1f1(Z1),Z2f2(Z2),···,Znfn(Zn))' ∈SS∗α,k+1(UN).Then

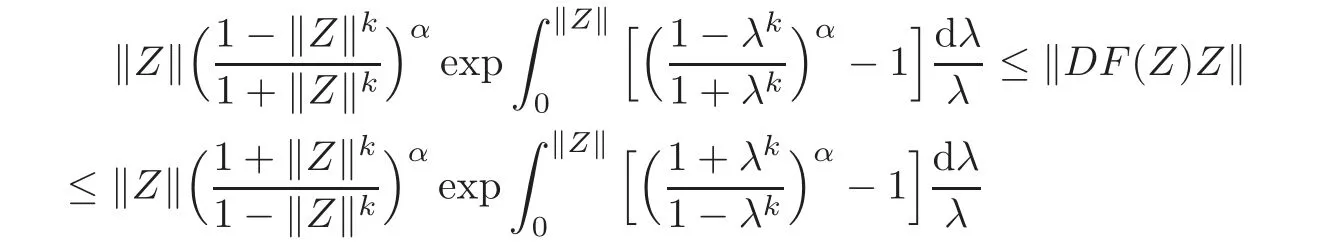
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Lettingin Theorem 2.2,where α ∈ [0,1),we derive the following corollary.

Corollary 2.9Letg:U→Csatisfy the condition of Definition1.1,fl:Uml→C∈H(Uml),l=1,2,···,n,and

(i)Ifα ∈ [0,1)and,then

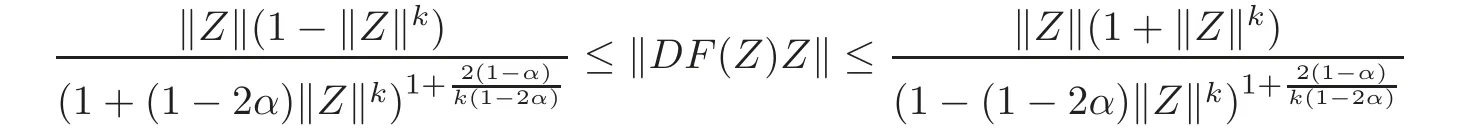
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

(ii)Ifα=,then

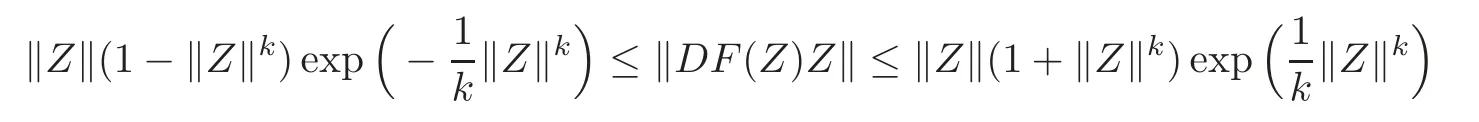
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Letting g(ξ)=in Theorem 2.2,where c ∈ (0,1),we get the following corollary.

Corollary 2.10Letg:U→Csatisfy the condition of Definition1.1,c∈(0,1),fl:Uml→C∈H(Uml),l=1,2,···,n,andThen

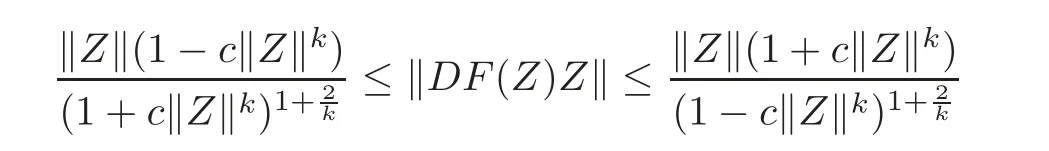
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Theorem 2.3Suppose thatg:U→Csatisfies the condition of Definition1.1,F(z)=(F1(z),F2(z),···,Fn(z))∈ H(Un),andz=0is a zero of orderk+1(k ∈ N)ofF(z)− z.Ifwherejsatisfies the conditionthen

forz=(z1,z2,···,zn)'∈ Un,and the above estimates are sharp.

ProofFix z∈Un{0},and we write.Define

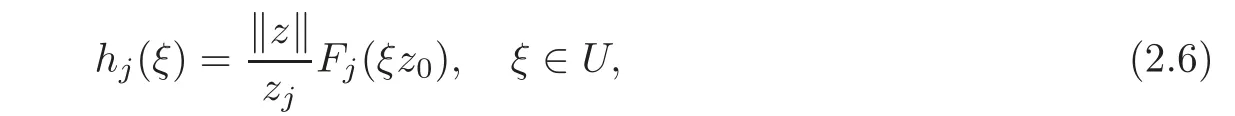
where j satisfies the conditionTaking into account the hypothesis of Theorem 2.3 and(2.6),we see that

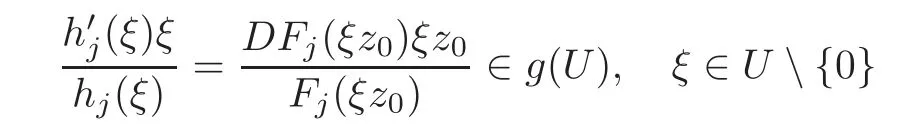
by a simple calculation.Thus it is shown that hj∈,and ξ=0 is at least a zero of order k+1 of hj(ξ)− ξ.

On the other hand,for z0∈ ∂Un,it yields that

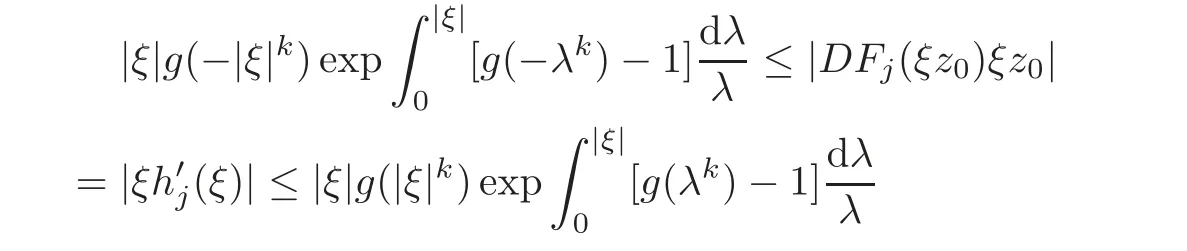
from Theorem 2.1(the case of X=C,B=U).It is readily known that

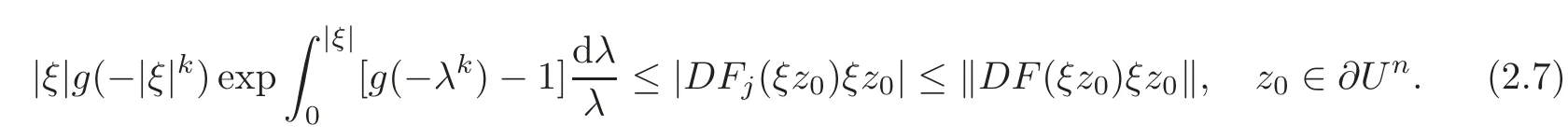
We set ξ=?z?.Then

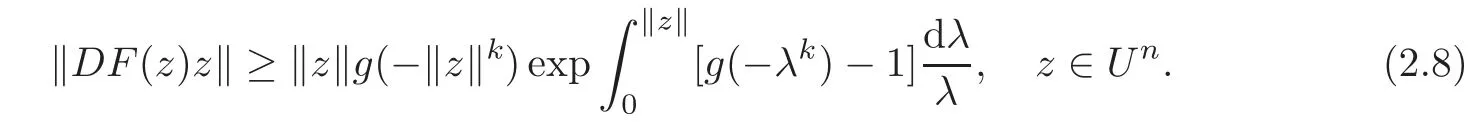
For z0∈ ∂0Un,we know that

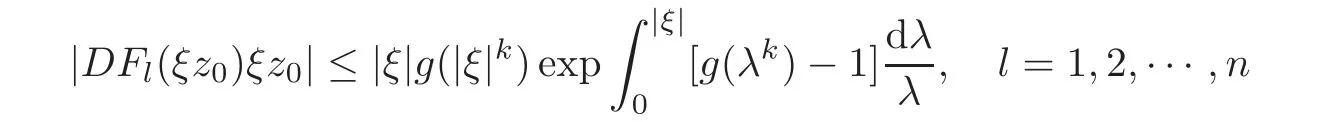
from(2.7).We mention that w(z)=DFl(ξz)ξz is a holomorphic function on Un.According to the maximum modulus theorem of holomorphic functions on the unit polydisk,it is shown that

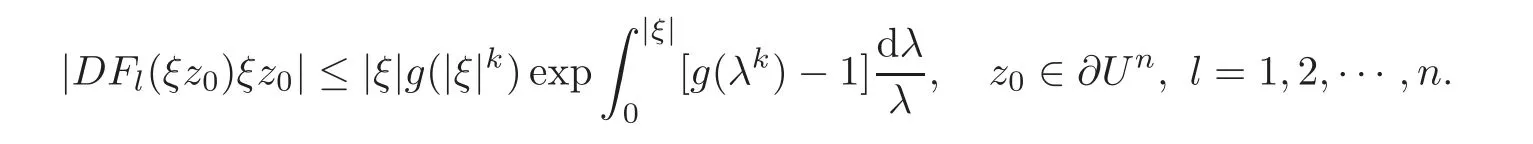
This implies that

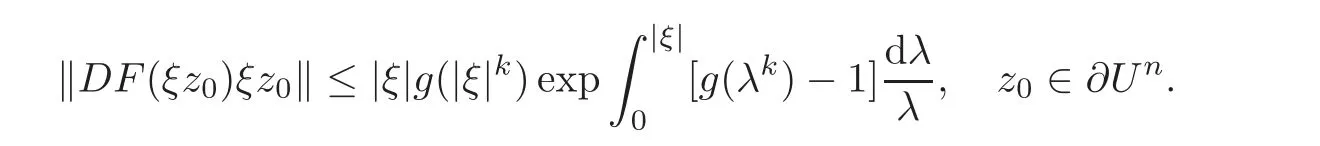
Taking ξ=?z?,it yields that

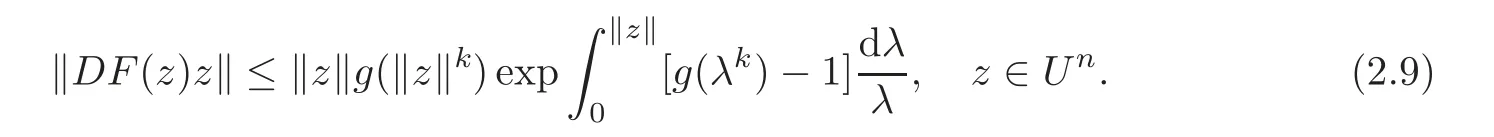
We derive the desired results from(2.8)–(2.9).The sharpness of the estimates of Theorem 2.3 is similar to that in the proof of Theorem 2.2,so the details are omitted here.This completes the proof.

Remark 2.3It is shown that Theorem 2.1(the case X=CnB=Un)is a special case of Theorem 2.3,and Theorem 2.2(the case m1=n,ml=0,l=2,···,n or ml=1,l=1,2,···,n)is also a special case of Theorem 2.3.

Set g(ξ)=in Theorem 2.3.Then we get the following corollary.

Corollary 2.11Suppose thatg:U→Csatisfies the condition of Definition1.1,F(z)=(F1(z),F2(z),···,Fn(z))∈ H(Un),andz=0is a zero of orderk+1(k ∈ N)ofF(z)− z.Ifwherejsatisfies the conditionthen

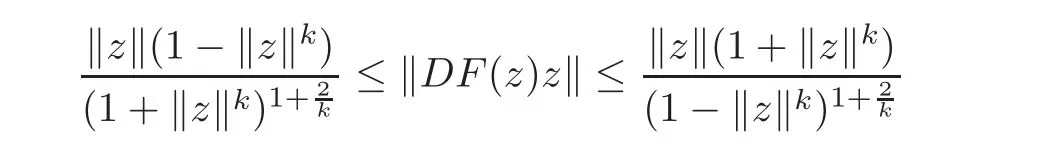
forz=(z1,z2,···,zn)'∈ Un,and the above estimates are sharp.

Setin Theorem 2.3,where α ∈ (0,1).Then we derive the following corollary.

Corollary 2.12Suppose thatg:U→Csatisfies the condition of Definition1.1,α∈(0,1),F(z)=(F1(z),F2(z),···,Fn(z))∈ H(Un),andz=0is a zero of orderk+1(k ∈ N)ofwherejsatisfies the conditionthen

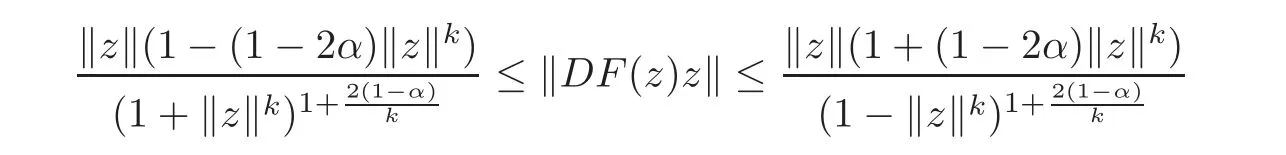
forz=(z1,z2,···,zn)'∈ Un,and the above estimates are sharp.

Set g(ξ)=in Theorem 2.3,where α ∈ (0,1].Then we obtain the following corollary.

Corollary 2.13Suppose thatg:U→Csatisfies the condition of Definition1.1,α∈(0,1],F(z)=(F1(z),F2(z),···,Fn(z))∈ H(Un),andz=0is a zero of orderk+1(k ∈ N)ofwherejsatisfies the conditionthen

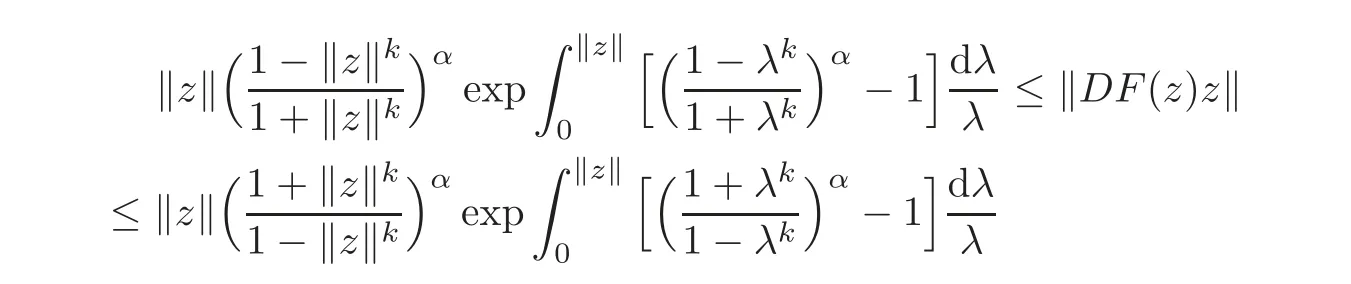
forz=(z1,z2,···,zn)'∈ Un,and the above estimates are sharp.

Set g(ξ)=in Theorem 2.3,where α ∈ [0,1).Then we get the following corollary.

Corollary 2.14Suppose thatg:U→Csatisfies the condition of Definition1.1,α∈[0,1),F(z)=(F1(z),F2(z),···,Fn(z))∈ H(Un),andz=0is a zero of orderk+1(k ∈ N)ofF(z)−z.Ifwherejsatisfies the conditionthen

(i)Ifα ∈ [0,1)andthen

forz=(z1,z2,···,zn)'∈ Un,and the above estimates are sharp.

(ii)Ifα=,then

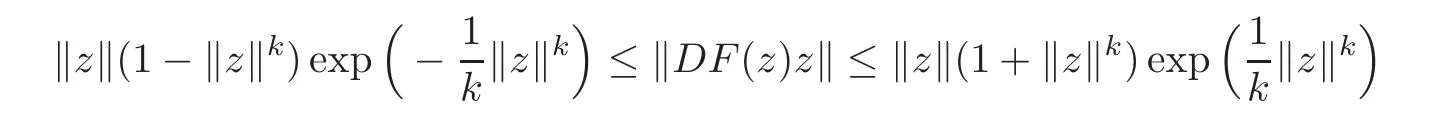
forz=(z1,z2,···,zn)'∈ Un,and the above estimates are sharp.

Set g(ξ)=in Theorem 2.3,where c∈ (0,1).Then we derive the following corollary.

Corollary 2.15Suppose thatg:U→Csatisfies the condition of Definition1.1,c∈(0,1),F(z)=(F1(z),F2(z),···,Fn(z)) ∈ H(Un),andz=0is a zero of orderk+1(k ∈ N)ofwherejsatisfies the condition|zj|=then

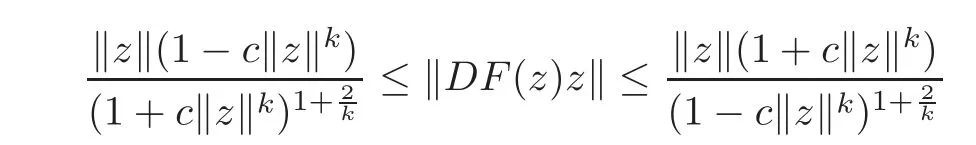
forz=(z1,z2,···,zn)'∈ Un,and the above estimates are sharp.

Remark 2.4From Theorems 2.1 and 2.2,we see that the forms of distortion theorems of the Fr´echet-derivative type for a subclass of starlike mappings are similar to each other.We may propose the following open problem.

Open Problem 2.1Suppose thatg:U→Csatisfies the condition of Definition1.1.Ifthen

and the above estimates are sharp.

3 Sharp Distortion Theorems of the Jacobi-Determinant Type for a Subclass of Biholomorphic Mappings Which Have a Parametric Representation

In this section,we denote by JF(z)the Jacobi matrix of the holomorphic mapping F(z),and let detJF(z)be the Jacobi determinant of the holomorphic mapping F(z).Also B is denoted by the unit ball of Cnwith an arbitrary norm,and Inis denoted by the unit matrix of Cn.We usually write vectors in Cnas column vectors in this section.

Theorem 3.1Letg:U→Csatisfy the condition of Definition1.1,f:B→C∈H(B),andF(z)=zf(z)∈(B).Then

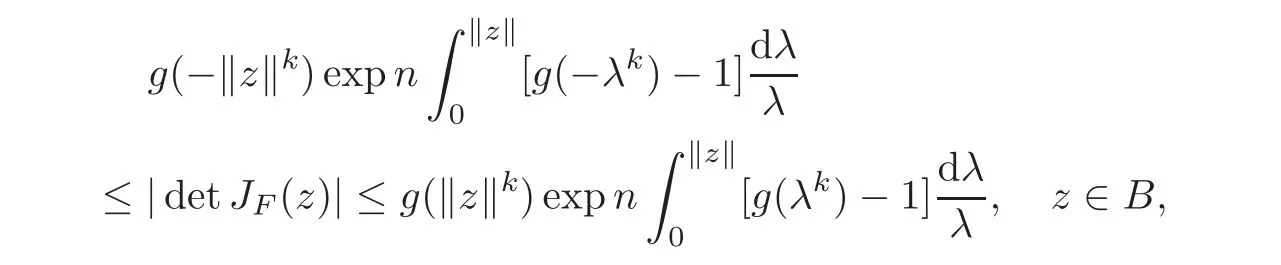
and the above estimates are sharp.

ProofSince F(z)=zf(z)∈(B),it is shown that

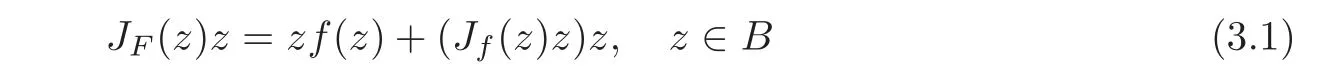
by a direct computation.With the same arguments as in the proof of Theorem 2.1,it yields thatfor z∈B,and

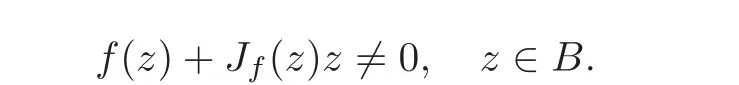
We see that

by a simple calculation.According to Lemma 2.1(the case of X=Cn),we see that

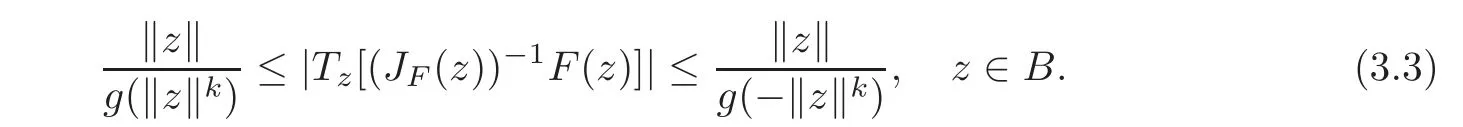
Also we deduce that

from(3.1).In view of(3.2),it yields that

Consequently,it is shown that

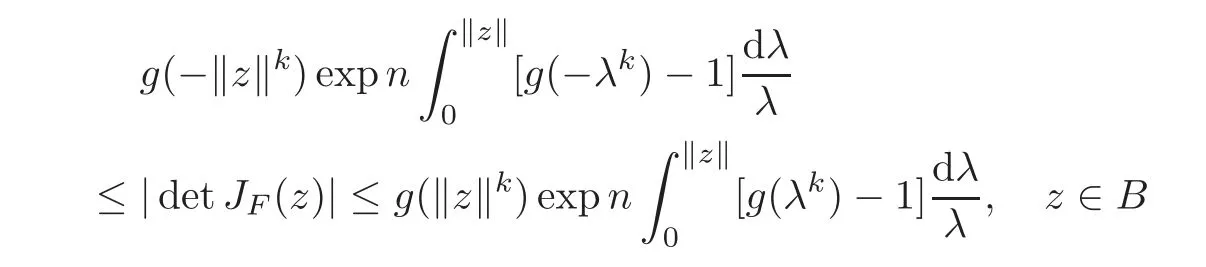
from Theorem 2.1(the case X=Cn)and(3.3).The sharpness of Theorem 3.1 is similar to that in the proof of Theorem 2.1.We omit the details here.This completes the proof.

Remark 3.1Taking k=1 in Theorem 3.1,it is easy to see that Theorem 3.1 generalizes[8,Theorem 4].

Setting g(ξ)=in Theorem 3.1,then we get the following corollary.

Corollary 3.1Letf:B→C∈H(B),andF(z)=zf(z)∈S∗k+1(B).Then

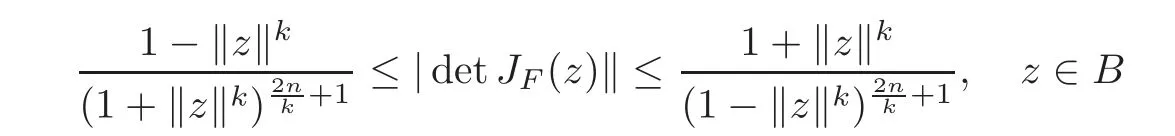
and the above estimates are sharp.

Letting g(ξ)=in Theorem 3.1,where α ∈ (0,1),we derive the following corollary.

Corollary 3.2Letf:B→C∈H(B),α∈(0,1),andF(z)=zf(z)∈Thenand the above estimates are sharp.

Setting g(ξ)=in Theorem 3.1,where α ∈ (0,1],we obtain the following corollary.

Corollary 3.3Letf:B→C∈H(B),α∈(0,1],andF(z)=zf(z)∈(B).Then

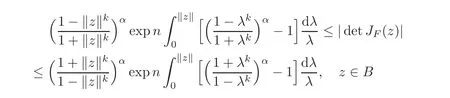
and the above estimates are sharp.

Let g(ξ)=in Theorem 3.1,where α ∈ [0,1).Then we derive the following corollary.

Corollary 3.4Letf:B→C∈H(B),andF(z)=zf(z)∈(B).

(i)Ifα ∈ (0,1)and,then

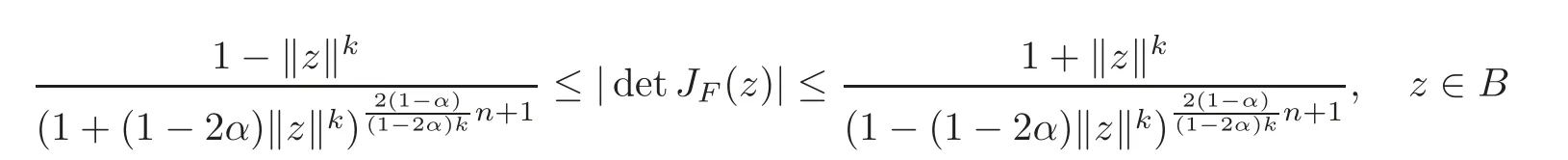
and the above estimates are sharp.

(ii)Ifα=,then

and the above estimates are sharp.

Setting g(ξ)=in Theorem 3.1,where c ∈ (0,1),we obtain the following corollary.

Corollary 3.5Letf:B→C∈H(B),c∈(0,1),andF(z)=zf(z)∈(B).Then

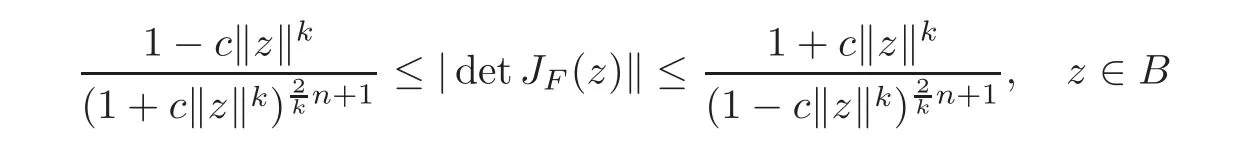
and the above estimates are sharp.

From now on,let each mlbe a non-negative integer,N=m1+m2+ ···+mn∈ N,and ml=0 means that the corresponding components in Z=(Z1,···,Zl,···,Zn)'and F(Z)=(F1(Z1),···,Fl(Zl),···,Fn(Zn))'are vanished.

Theorem 3.2Letg:U→Csatisfy the condition of Definition1.1,fl:Uml→C∈H(Uml),l=1,2,···,n,andThen

forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

ProofAccording to the conditions of Theorem 3.2,for any Z=(Z1,Z2,···,Zn)'∈ UN,it yields that

With the same arguments as in the proof of Theorem 2.2,we have that

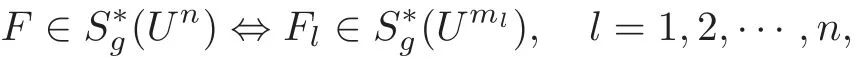
and Zl=0 is at least a zero of order k+1 of each Fl(Zl)−Zl(l=1,2,···,n)if Z=0 is a zero of order k+1 of F(Z)−Z.Note that1](l=1,2,···,n))is a decreasing function(resp.an increasing function)on the interval[0,1)with respect to t.Also,

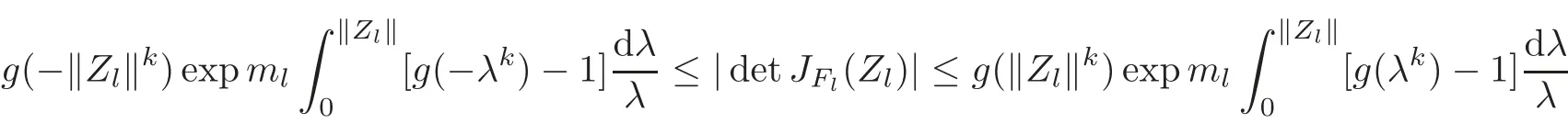
for Zl∈ Uml(l=1,2,···,n).Hence the desired results follow from(3.4).The sharpness of Theorem 3.2 is similar to that in the proof of Theorem 2.2.The details are omitted here.This completes the proof.

Letting g(ξ)=in Theorem 3.2,we get the following corollary.

Corollary 3.6Letg:U→Csatisfy the condition of Definition1.1,fl:Uml→C∈H(Uml),l=1,2,···,n,andThen

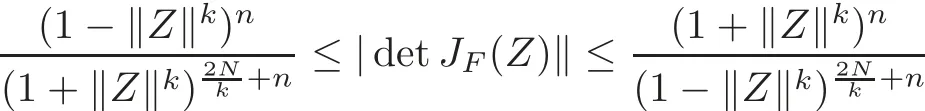
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Let g(ξ)=in Theorem 3.2,where α ∈ (0,1).Then we derive the following corollary.

Corollary 3.7Letg:U→Csatisfy the condition of Definition1.1,α∈(0,1),fl:Uml→ C ∈ H(Uml),l=1,2,···,n,and

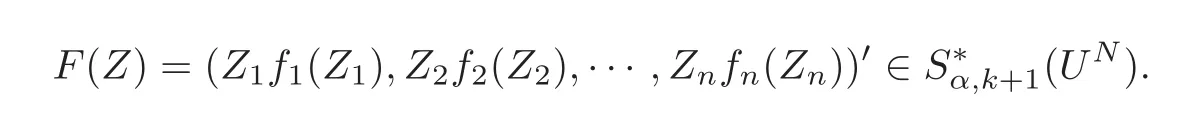
Then

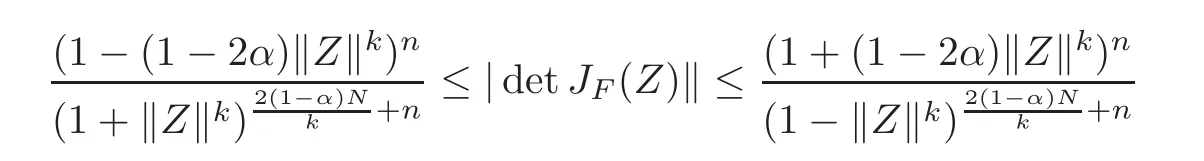
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

We set g(ξ)=in Theorem 3.2,where α ∈ (0,1].Then it is obvious to show that the following corollary holds.

Corollary 3.8Letg:U→Csatisfy the condition of Definition1.1,α∈(0,1],fl:Uml→ C ∈ H(Uml),l=1,2,···,n,andF(Z)=(Z1f1(Z1),Z2f2(Z2),···,Znfn(Zn))' ∈Then

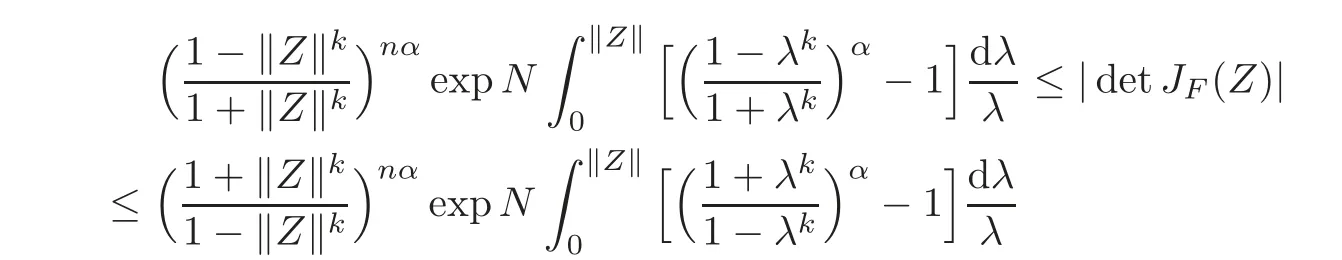
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Let g(ξ)=in Theorem 3.2,where α ∈ [0,1).Then we derive the following corollary.

Corollary 3.9Letg:U→Csatisfy the condition of Definition1.1,fl:Uml→C∈H(Uml),l=1,2,···,n,and

(i)Ifα ∈ (0,1)andthen

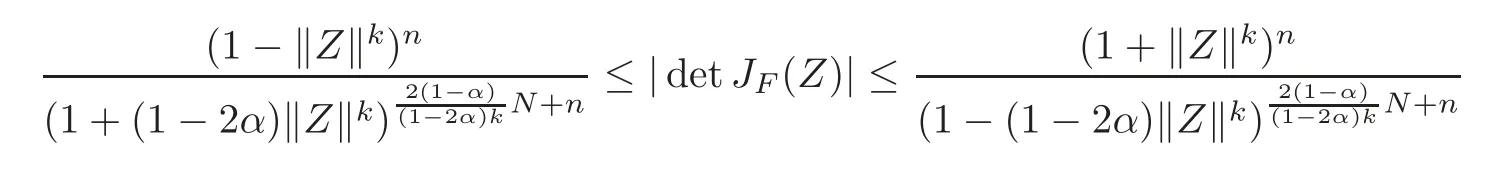
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

(ii)Ifα=,then

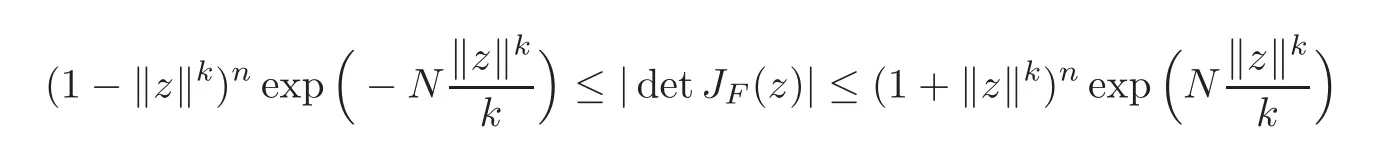
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Let g(ξ)=in Theorem 3.2,where c∈ (0,1).Then we get the following corollary.

Corollary 3.10Letg:U→Csatisfy the condition of Definition1.1,c∈(0,1),fl:Uml→C∈H(Uml),l=1,2,···,n,andThen

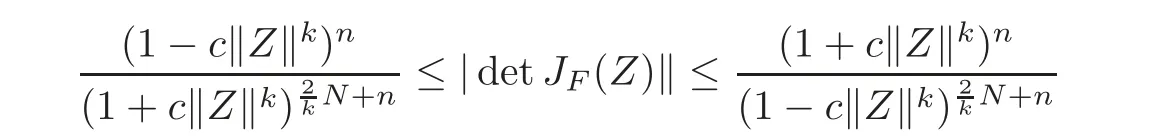
forZ=(Z1,Z2,···,Zn)'∈ UN,and the above estimates are sharp.

Remark 3.2In view of Theorem 3.2(the case ml=1,l=1,2,···,n),we may propose the following open problem.

Open Problem 3.1Letg:U→Csatisfy the condition of Definition1.1,andF∈Then

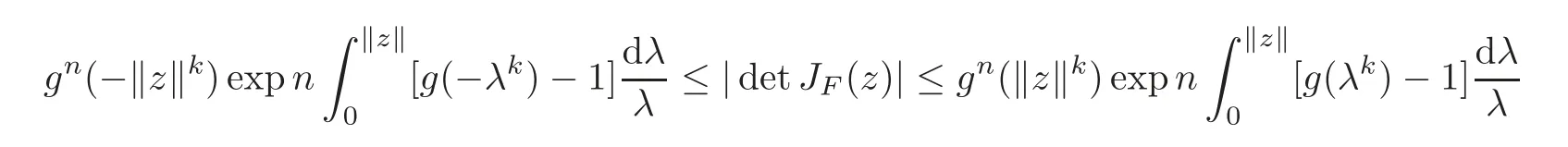
forz∈Un,and the above estimates are sharp.

AcknowledgementThe authors would like to thank the referees for their helpfulcomments.

[1]Poreda,T.,On the univalent holomorphic maps of the unit polydisc of Cnwhich have the parametric representation,I—the geometric properties,Ann.Univ.Mariae Curie Sklodowsda Sect.A,41,1987,105–113.

[2]Kohr,G.,Using the method of Löwner chains to introduce some subcalsses of biholomorphic mappings in Cn,Rev.Roum.Math.Pures Appl.,46,2001,743–760.

[3]Graham,I.,Hamada,H.and Kohr,G.,Parametric representation of univalent mappings in several complex variables,Canadian J.Math.,54(2),2002,324–351.

[4]Kubicka,E.and Poreda,T.,On the parametric representation of starlike maps of the unit ball in Cninto Cn,Demonstration Math.,21,1988,345–355.

[5]Kohr,G.and Liczberski,P.,Univalent Mappings of Several Complex Variables,Cluj University Press,Cluj-Napoca,Romania,1998.

[6]Hamada,H.,Honda,T.and Kohr,G.,Growth theorems and coefficient bounds for univalent holomorphic mappings which have parametric representation,J.Math.Anal.Appl.,317(1),2006,302–319.

[7]Hamada,H.and Honda,T.,Sharp growth theorems and coefficient bounds for starlike mappings in several complex variables,Chin.Ann.Math.Ser.B,29(4),2008,353–368.

[8]Xu,Q.H.and Liu,T.S.,Sharp growth and distortion theorems for a subclass of biholomorphic mappings,Computer Math.Appl.,59(12),2010,3778–3784.

[9]Xu,Q.H.,Liu,T.S.and Xu,H.M.,Growth and distortion theorems for a subclass of holomorphic mappings in several complex variables,Chin.Ann.Math.Ser.A,35(5),2014,565–574(in Chinese).

[10]Barnard,R.W.,FitzGerald C.H.and Gong S.,A distortion theorem of biholomorphic convex mappings in C2,Trans.Amer.Math.Soc.,344(2),1994,907–924.

[11]Liu,T.S.and Zhang,W.J.,A distortion theorem of biholomorphic convex mappings in Cn,Chin.Ann.Math.Ser.A,20(4),1999,505–512(in Chinese).

[12]Gong,S.,Wang,S.K.and Yu,Q.H.,Biholomorphic convex mappings of ball in Cn,Pacif.J.Math.,161(2),1993,287–306.

[13]Gong,S.and Liu,T.S.,Distortion theorems for biholomorphic convex mappings on bounded convex circular domains,Chin.Ann.Math.Ser.B,20(3),1999,297–304.

[14]Liu,T.S.and Zhang,W.J.,A distortion theorem of biholomorphic convex mappings in a Banach space,Acta Math.Sin.,46(6),2003,1041–1046(in Chinese).

[15]Zhu,Y.C.and Liu,M.S.,Distortion theorems for biholomorphic convex mappings in Banach spaces,Complex Variables,50(1),2005,57–68.

[16]Chu,C.H.,Hamada,H.,Honda T.and Kohr G.,Distortion theorems for convex mappings on homogeneous balls,J.Math.Anal.Appl.,369(2),2010,437–442.

[17]Hamada,H.and Kohr,G.,Growth and distortion results for convex mappings in in finite dimensional spaces,Complex Variables,47(4),2002,291–301.

[18]Liu,T.S.,Wang,J.F.and Lu,J.,Distortion theorems for starlike mappings in several complex variables,Taiwanese J.Math.,15(6),2011,2601–2608.

[19]Liu,X.S.and Liu,T.S.,On the sharp distortion theorems for a subclass of starlike mappings in several complex variables,Taiwanese J.Math.,19(2),2015,363–379.

[20]Hamada,H.,Kohr,G.and Liczberski,P.,Starlike mappings of order α on the unit ball in complex Banach spaces,Glas.Mat.Ser.III,36(1),2001,39–48.

[21]Xu,Q.H.and Liu,T.S.,On coefficient estimates for a class of holomorphic mappings,Sci.China Ser.A-Math.52(4),2009,677–686.

[22]Kohr,G.and Liczberski,P.,On strongly starlikeness of order α in several complex variables,Glas.Mat.,33(53),1998,185–198.

[23]Feng,S.X.and Lu,K.P.,The growth theorem for almost starlike mappings of order α on bounded starlike circular domains,Chin.Quart.J.Math.,15(2),2000,50–56.

[24]Chuaqui,M.,Applications of subordination chains to starlike mappings in Cn,Pacif.J.Math.,168(1),1995,33-48.

[25]Honda,T.,The growth theorem for k-fold symmetric convex mappings,Bull.London Math.Soc.,34(6),2002,717–724.

[26]Lin,Y.Y.and Hong,Y.,Some properties of holomorphic maps in Banach spaces,Acta Math.Sin.,38(2),1995,234–241(in Chinese).