Abstract Elliptic Equations with Integral Boundary Conditons
2016-05-28VeliSHAKHMUROV
1 Introduction
Boundary value problems(for short BVPs)for differential-operator equations(for short DOEs)have been studied extensively by many researchers(see[1–3,8,10–11,14–23,25–32]and the references therein).A comprehensive introduction to the DOEs and historical references may be found in[16,28].The maximal regularity properties for differential-operator equations have been investigated,e.g.,in[1,8,10–11,17–22,26,28,30–32].
In recent years,integral boundary conditions(for short IBC)for evolution problems have found many applications in various disciplines such as chemical engineering,thermoplasticity,underground water flow and population dynamics(see[4,7,9,13,24]and the references therein).
The main purpose aim of the present paper,is to show the separability properties of the integral boundary value problem(for short IBVP)for the following DOE:
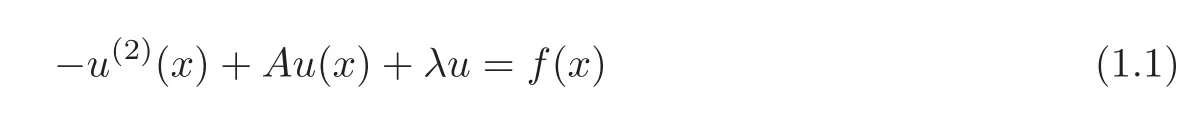
and maximal regularity of Cauchy problem for the following abstract parabolic equation:
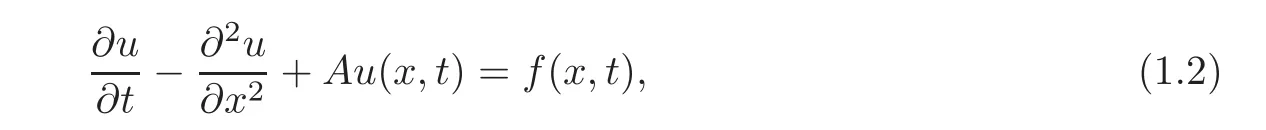
with integral boundary conditions,where A is a linear operator in the Banach space E and λ is a complex parameter.
Unlike the previous results,the boundary conditions here contain nonlocal integral terms.The maximal Lp-regularity and the Fredholmness are obtained.Moreover,it is proven that the corresponding elliptic operator is R-positive and is a generator of an analytic semigroup.These results are applied to nonlocal BVPs for partial differential equations and it’s finite or in finite systems on cylindrical domains.
We shall prove the separability of the problem(1.1),i.e.,we show that for each f∈Lp(0,1;E),there exists a unique strong solution u of the problem(1.1)and the following uniform coercive estimate holds:
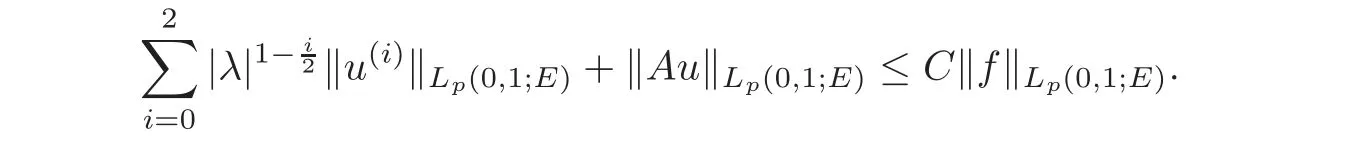
Let E be a Banach space and Lp(Ω;E)denotes the space of strongly measurable E-valued functions that are defined on the measurable subset Ω⊂Rnwith the norm
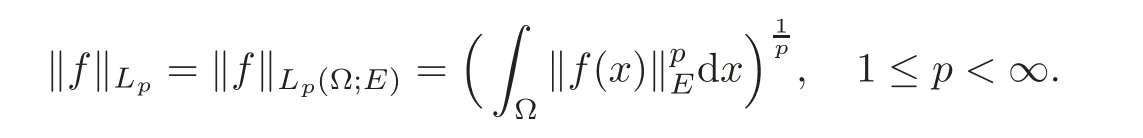
The Banach space E is called a UMD-space if the Hilbert operator
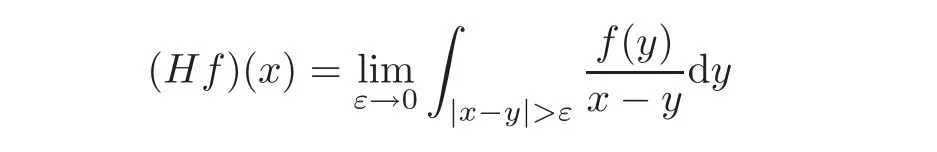
is bounded in Lp(R,E),p ∈ (1,∞)(see[6]),where R=(−∞,∞).UMD spaces include,e.g.,Lp,lpspaces and Lorentz spaces Lpq,p,q∈(1,∞).
Let C be the set of the complex numbers and

A linear operator A is said to be ϕ-positive in a Banach space E with bound M>0 if D(A)is dense on E and
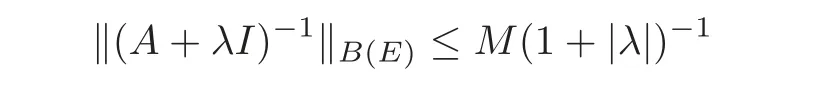
for any λ ∈ Sϕ,0 ≤ ϕ < π,where I is the identity operator in E,and B(E)is the space of bounded linear operators in E.Sometimes A+λI will be written as A+λ and denoted by Aλ.It is known in[27,§1.15.1]that there exist the fractional powers Aθof a positive operator A.Let E(Aθ)denote the space D(Aθ)with norm
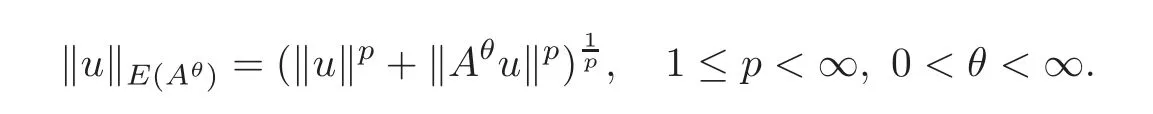
Let E1and E2be two Banach spaces.By(E1,E2)θ,p,0< θ<1,1≤ p≤ ∞,we denote the interpolation spaces obtained from{E1,E2}by the K-method(see[27,§1.3.2]).
Let S(Rn;E)denote the Schwartz class,i.e.,the space of all E-valued rapidly decreasing smooth functions on Rn.Let F denote the Fourier transformation.A function Ψ∈C(Rn;B(E1,E2))is called a Fourier multiplier from Lp(Rn;E1)to Lp(Rn;E2)if the map u → Λu=F−1Ψ(ξ)Fu,u ∈ S(Rn;E1)is well defined and extends to a bounded linear operator

The set of all multipliers from Lp(Rn;E1)to Lp(Rn;E2)will be denoted by(E1,E2).For E1=E2=E,it will be denoted by(E).The most important facts about Fourier multipliers and some related references,can be found in[11–12,27,30].
Let Φh={Ψh∈(E1,E2),h ∈ Q}be a collection of multipliers.We say that Whis a uniform collection of multipliers if there exists a positive constant M independent of h∈Q such that

for all h∈Q and u∈S(Rn;E1).
Let N denote the set of natural numbers.A set G⊂B(E1,E2)is called R-bounded(see[10])if there is a positive constant C such that for all T1,T2,···,Tm∈ G and u1,u2,···,um∈ E1,m∈N,
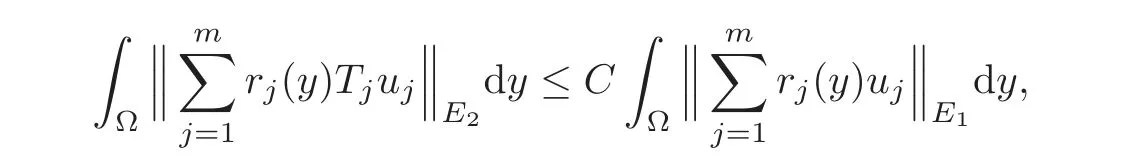
where{rj}is a sequence of independent symmetric{−1,1}-valued random variables on Ω (see[11]).The smallest C for which the above estimate holds is called an R-bound of the collection G and denoted by R(G).
A set Gh⊂B(E1,E2)depending on parameter h∈Q is called uniformly R-bounded with respect to h if there exists a constant C,independent of h∈Q,such that for all T1(h),T2(h),···,Tm(h)∈ Ghand u1,u2,···,um∈ E1,m ∈ N,

It implies thatLet
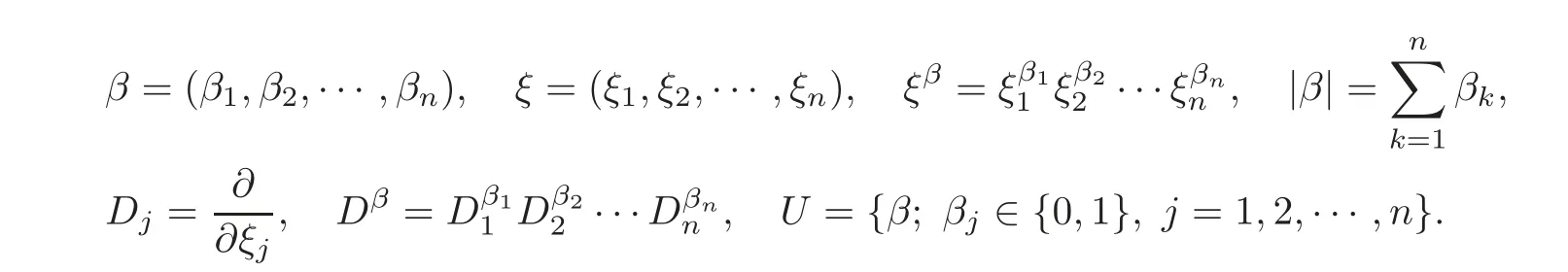
Definition 1.1A Banach spaceEis said to be a space satisfying a multiplier condition if,for anyΨ∈C(n)(Rn;B(E)),theR-boundedness of theimplies thatΨis a Fourier multiplier,i.e.,for anyp∈(1,∞).
The uniform R-boundedness of the
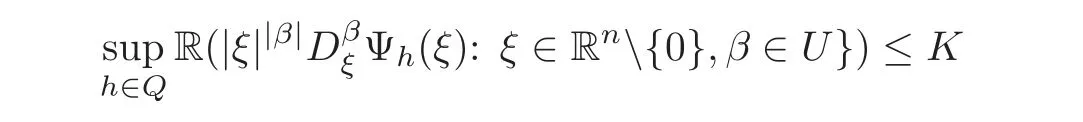
implies that Ψhis a uniform collection of Fourier multipliers.
Remark 1.1Definition 1.1 is a restriction on the Banach spaces E.If E is a UMD space,then this space satisfies the multiplier condition.All UMD spaces satisfy the multiplier condition(see[12]).
The ϕ-positive operator A is said to be R-positive in a Banach space E if the set

is R-bounded.
Note that in Hilbert spaces,all norm-bounded sets are R-bounded.Therefore,in Hilbert spaces,all positive operators are R-positive.If A is the generator of a contraction semigroup on Lq,1≤ q ≤ ∞ or A has the bounded imaginary powers with(see[11])in E∈UMD,then those operators are R-positive.
Let D(Ω;E)denote the class of all E-valued in finite differentiable functions on domain Ω with compact supports.For E=C,denotes it by D(Ω).
Let σ∞(E)denote the space of all compact operators in E.Let E0and E be two Banach spaces and E0be continuously and densely embedded into E.Let m be a positive integer.Let us consider the spaceconsisting of all functions u ∈ Lp(Ω;E0)that have the generalized derivativeswith the norm
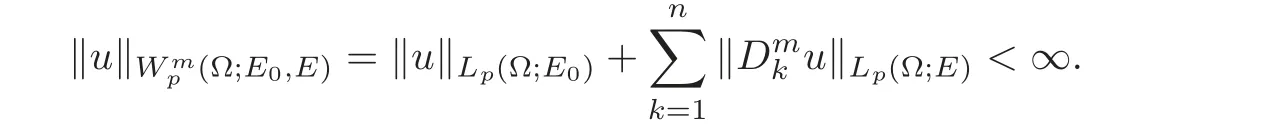
For Ω =(a,b),a,b ∈ (−∞,∞),the spacewill be denoted byand for E0=E,denotes it by
By using the techniques of[12,Theorem 3.7]we obtain the following proposition.
Proposition 1.1LetE1andE2be two UMD spaces and
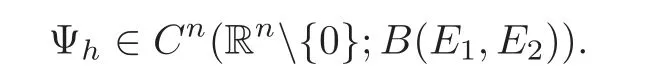
Suppose that there exists a positive constantKsuch that

ThenΨhis a uniform collection of multipliers fromLp(Rn;E1)toLp(Rn;E2)forp ∈ (1,∞).
From[21,Theorem 4]we obtain the following theorem.
Theorem 1.1Let the following conditions be satisfied:
(1)Eis a Banach space satisfying the uniform multiplier conditionp∈(1,∞)and0 (2)mis a positive integer andα =(α1,α2,···,αn)aren-tuples of nonnegative integer numbers such that (3)Ais anR-positive operator inEwith0≤ϕ<π; (4)Ω∈Rnis a region such that there exists a bounded linear extension operator betweenfromand fromLp(Ω;E)toLp(Rn;E). Then the embeddingis continuous and there ex-ists a positive constantCμsuch thatfor alland0 Remark 1.2If Ω ⊂ Rnis a region satisfying m-horn condition(see[5,§7]),E=R,A=I,then for p∈ (1,∞)there exists a bounded linear extension operator from From[21,Theorem 6]we obtain the following theorem. Theorem 1.2Suppose that all conditions of Theorem1.1are satisfied.Let0<μ≤1−κ.Then the embedding is continuous and there exists a positive constantCμsuch that for alltheuniform estimate holds,i.e., Remark 1.3Note that the constant Cμin the above estimate depends only on h0,μ and T.Since these numbers are bounded and fixed,this dependence does not in fluence the further results. Theorem 1.3(see[22])LetEbe a Banach space andAbe aϕ-positive operator inEwith boundM,0≤ ϕ < π.Letmbe a positive integer,Then forn operatorgenerates a semigroupwhichis holomorphic forx>0.Moreover,there exists a positive constantC(depending only onM,ϕ,m,αandp)such that for everyandλ ∈Sϕ, From[28,§1.7.7,Theorem 2]we obtain the following theorem. Theorem 1.4Letmandjbe integer numbers,Then,forthe transformationsare bounded linearly fromand the following inequality holds: By using the integral representation formula,in a similar way as in[5,§10.1]we have the following theorem. Theorem 1.5Letmandjbe integer numbers,Then,forthe transformationbounded linearly fromontoEand the following inequality holds: Let A be a positive operator in a Banach space E.Consider the differential-operator equation Let ω1,ω2,···,ωmbe the roots of the equation and where q is some integer number from(1,m). A system of complex numbers ω1,ω2,···,ωmis called q-separated if there exists a straight line P passing through 0 such that no value of the numbers ωjlies on it,and ω1,ω2,···,ωqare on one side of P while ωq+1,···,ωmare on the other side. Lemma 1.1(see[20])Let the following conditions be satisfied: (1)andωj,j=1,···,m,areq-separated; (2)Eis a Banach space satisfying the multiplier condition forp∈(1,∞); (3)Ais anR-positive operator inE. Then for a functionu(x)to be a solution of Equation(1.4),which belongs to the spaceE(A),E),it is necessary thatwhere In a Banach space E,consider the integral boundary value problem where f ∈ Lp(0,1;E),fk∈ Ek=(E(A),E)αk,p,p∈ (1,∞);A and Bkare linear operators in E and λ is a complex parameter. Let us first consider the following problem: where λ is a complex parameter,A and Bkare linear operators in E,Ek=(E(A),E)αk,p. Remark 3.1Let A be a positive operator in E.By definition,the operator Aλ=A+λ is ϕ1-positive in E for|argλ| ≤ ϕ and ϕ + ϕ1< π.From the beginning of the proof of[28,Lemma 5.4.2/4],for|argλ|≤ ϕ and|argμ|≤ ϕ1,ϕ,ϕ1∈ (0,π),we have the estimate with M0depending on ϕ only.Then in view of[8,Lemma 2.6],there exist semigroups U1λ(x)=which are holomorphic for x>0 and strongly continuous for x≥0. Let Condition 3.1Assume that (1)E is a Banach space satisfying the multiplier condition and η0; (2)A is an R-positive operator in E; (3)D(Bk) ⊂ (E(A),E)κ+ε,pforand (4)the operators u→Lku are bounded from(0,1;E(A),E)into Ek. Theorem 3.1Suppose that Condition3.1is satisfied.Then,the problem(3.1)–(3.2)forfk∈ Ek,p ∈ (1,∞)andλ ∈ Sϕwith sufficiently large|λ|has a unique solutionu ∈(0,1;E(A),E)and the following coercive uniform estimate holds: ProofBy virtue of Lemma 1.1 and Remark 1.3,an arbitrary solution of Equation(3.2)belonging to the space(0,1;E(A),E),has the form where Now taking into account boundary conditions(3.3)we obtain the algebraic linear equations with respect to g1,g2: Since the operator determinant η0,the system(3.5)has the solutionwhere Hence,the problem(3.1)–(3.2)has a solution given bellow By virtue of[8,Lemma 2.6],we have In view of(3.6),by estimate(3.7),the condition 3.1(2)and in view of the positivity of A,we obtain Hence,from Theorem 1.3 we obtain the assertion Now consider IBVPs for non-homogenous equation Theorem 4.1Suppose that Condition3.1is satisfied.Then the operatoru→{(L+λ)u,L1u,L2u}for|argλ|≤ ϕ,0 ≤ ϕ < πand sufficiently large|λ|,is an isomorphism from(0,1;E(A),E)ontoLp(0,1;E)× E1× E2.Moreover,for theseλ,the following uniform coercive estimate holds: ProofWe have proved the uniqueness of solution of the problem(4.1)–(4.2)in Theorem 3.1.By definition of(0,1;E(A),E)and by(4)of Condition 3.1,it is easy to see that the operator u→{(L+λ)u,L1u,L2u}is bounded from(0,1;E(A),E)into Lp(0,1;E)×E1×E2.Hence,by the Banach theorem,it is sufficient to show that the operator u→{(L+λ)u,L1u,L2u}is surjective from(0,1;E(A),E)into Lp(0,1;E)×E1×E2.Let us define We now show that the problem(4.1)–(4.2)has a solution u ∈(0,1;E(A),E)for all f∈Lp(0,1;E),fk∈Ekand u=u1+u2,where u1is the restriction on[0,1]of the solution of the equation and u2is a solution of the problem By virtue of Theorem 3.1,the problem(4.4)has a unique solution A solution of Equation(4.4)is given by the formula where L(λ,ξ)=A+ ξ2+ λ.It follows from the above expression that Let us show that operator-functions are Fourier multipliers in Lp(R;E)uniformly with respect to λ.In fact,due to positivity of A and by virtue of[8,Lemma 2.3]we have the following uniform estimates: It is clear to see that Due to R-positivity of the operator A,the sets are R-bounded.Then in view of the Kahane’s contraction principle and from the product properties of the collection of R-bounded operators(see[11,Lemma 3.5,Proposition 3.4])we obtain That is to say,the R-bound of the set is independent of λ.Next,let us consider σλ(ξ).It is clear to see that Then by using the well-known inequality yj≤ C(1+ym),y ≥ 0,j ≤ m for y=(|λ|−1l|ξ|)jand m=2,we get the uniform estimate From(4.7)–(4.8)we have Due to the R-positivity of the operator A,the set is R-bounded.Then from the equality and by Kahane’s contraction principle we obtain the R-boundedness of set Now by differentiating σλ(ξ)we have Consider the set Due to the R-positivity of the operator A,the sets are R-bounded.Then from the above formula in view of estimate(4.7),by virtue of the Kahane’s contraction principle and from the product and additional properties of the collection of R-bounded operators,for all ξ1,ξ2,···,ξm∈ R, σk(ξ1,λ), σ(ξ2,λ),···,σ(ξm,λ),u1,u2,···,um∈ E and independent symmetric{−1,1}-valued random variables rj(y),j=1,2,···,m,m ∈ N,we obtain the uniform estimate i.e., Then in view of Definition 1.1,it follows that Ψλ(ξ)and σλ(ξ)are the uniform collection of multipliers in Lp(R;E).Then,by using the equality(4.6)we obtain that the problem(4.4)has a solution u∈(R;E(A),E)and the uniform estimate holds,i.e., Let u1be the restriction of u on(0,1).Then the estimate(4.9)implies that By virtue of Theorem 1.5,we get Hence,Lku1∈Ek.Thus by virtue of Theorem 4.1,the problem(4.9)has a unique solution u2(x)that belongs to the space(0,1;E(A),E)and for sufficiently large|λ|we have Moreover,from(4.10),for|argλ|≤ ϕ we obtain By Theorem 4.1,we have Finally,from(4.11)–(4.12)we obtain the estimate(4.3). Consider the problem Let B denote the operator in F=Lp(0,1;E)generated by the problem(4.13)–(4.14),i.e., Theorem 4.1 implies the following corollary. Corollary 4.1Suppose that Condition 3.1 is satisfied.Then for sufficiently large k>0,there exist positive constants C1and C2so that for u∈W(0,1,E(A),E). Theorem 4.2Suppose that Condition3.1is satisfied.Then the operatorBis uniformlyR-positive inLp(0,1;E). ProofThe estimate(4.3)implies that,for λ ∈ Sϕand enough large|λ|,B+ λ is invertible and the operator B is positive in Lp(0,1;E).By using a similar technique as in[28,Lemma 5.3.2/1],we obtain that,for f∈D(0,1;E(A)),the solution of the Equation(4.13)is represented as where andare analytic semigroups generated by operatorBy taking into account the boundary conditions(4.14),we obtain the following equation with respect to g1and g2: By solving the above system and substituting it into(4.15),in a similar way as in Theorem 3.1,we obtain the representation of the solution for the problem(4.13)–(4.14): where Ckjandare the same as in(3.6).By calculating Lk(Φλ)we obtain from the above where Bkj(λ)are like.So are the uniformly bounded operators in E and Let us first show that the set{G(λ,x,y);λ ∈ S(ϕ)}is uniformly R-bounded.Really,by using the generalized Minkowcki’s Young inequalities,by semigroup estimates(3.7),have the uniform estimate Due to R-positivity of A,in view of properties of holomorphic semigroups Ujλ(x)and the uniform boundedness of operators Bkj(λ)and by using the Kahane’s contraction principle,we get that the sets are uniformly R-bounded.Then by using the Kahane’s contraction principle,product and additional properties of the collection of R-bounded operators and the R-boundedness of the sets bkj,d0for all u1,u2,···,uμ∈ F, λ1,λ2,···,λμ∈ S(ϕ),for independent symmetric{−1,1}-valued random variables ri(y),i=1,2,···,μ, μ ∈ N,we have the estimate uniformly in x and y.This implies that In view of R-bondedness property of kernel operators(see[11,Proposition 4.12])and due to the density of D(0,1;E(A))in Lp(0,1;E)(see[23]),we obtain the assertion. Consider the problem In this section we obtain the well-posedeness of problem(4.14)in mixed Lpspace. If G+=(0,∞)× (0,1),p=(p,p1),Lp(G+;E)will denote the space of all p-summable scalar-valued functions with mixed norm(see,[5,§1]for E=C),i.e.,the space of all measurable functions f defined on G,for which Analogously,(G+;E)denotes the E-valued Sobolev space with corresponding mixed norm(see,[5,§10]for E=C). Theorem 5.1Suppose that Condition3.1is satisfied forϕ ∈ (,π).Then forf ∈ Lp(G+;E)and sufficiently largea>0,the problem(5.1)has a unique solution belonging toE(A),E)and the uniform estimate holds,i.e., ProofThe problem(4.14)can be express as the following Cauchy problem: Theorem 4.2 implies that the operator O is uniformly R-positive and is a generator of analytic semigroups in F=Lp(0,1;E).Then by virtue of[30,Theorem 4.2],we obtain that for all f∈Lp1(R+;F),the problem(4.15)has a unique solution belonging to(R+;D(B),F)and the following estimate holds: Since Lp1(R+;F)=Lp(G+;E),by Theorem 4.1 we have These relations and the above estimate imply the assertion. The Fredholm property of BVPs for elliptic equations with parameters in smooth domains was studied in[1].In this section,the coercive estimate on the solution of integral boundary conditions for elliptic equations will be established in mixed Lpspaces. Let G⊂Rm,m≥2,be a bounded domain with an(m−1)-dimensional boundary∂G∈C∞which locally admits rectification.Consider the following nonlocal BVP for the following anisotropic elliptic equation: where Bk(x)are bounded operator fromto Lp1(G)fordenotes the Besov space[6,§18]. Dx=,Dj=,Dy=(D1,···,Dm),mk∈{0,1},αk,βkare complex numbers,r=0 or r=1,y=(y1,···,ym).Let Q denote the operator generated by problem(6.1)–(6.3)for λ=0. If Ω =(0,1)× G,p=(p1,p),Lp(Ω)will denote the space of all p-summable scalar-valued functions with a mixed norm(see,[5,§1]),i.e.,the space of all measurable functions f defined on Ω,for which Analogously,(Ω)denotes the Sobolev space with corresponding mixed norm(see[6,§10]). We have the result as following theorem. Theorem 6.1Let the following conditions be satisfied: (1)Bkare bounded operators from (2)aα∈ C(Ω)for each|α|=2mandaα∈ [L∞+Lrk](Ω)for each|α|=k<2mwithrk≥p1,p1∈(1,∞)and (3)bjβ∈ C2m−mj(∂Ω)for eachj,β,mj<2m,p ∈ (1,∞); (4)fory ∈ Ω,ξ∈ Rμ,η ∈ S(ϕ1),ϕ1∈ [0,),|ξ|+|η|0,let (5)for eachy0∈ ∂Ω,the local BVP’s in local coordinates corresponding toy0 has a unique solutionϑ ∈ C0(R+)for allh=(h1,h2,···,hm) ∈ Rmand forξ'∈ Rμ−1with Then (a)for allf ∈ Lp(Ω),p=(p1,p),andsufficiently large|λ|,the problem(6.1)–(6.3)has a unique solutionu ∈and the following coercive uniform estimate holds: (b)the operatoru → Qu={Lu,L1u,L2u}is Fredholm from(Ω)intoLp(Ω)× ProofLet E=Lp1(G).Consider the operator A defined by Then the problem(6.1)–(6.3)can be rewritten in the form of(2.1),(3.1),i.e., Let us apply Theorem 4.1 to problem(6.4).It is known that Lp1(G)∈ UMD for p1∈ (1,∞)(see[3]).Then in view of the multiplier theorems in E-valued Lpspaces(see[30]),the space Lp1(G)satisfies the multiplier condition.By virtue of[11,Theorem 8.2],the operator A is R-positive in Lp1(G)and has the fractional powers,i.e.,all conditions of the Theorem 4.1 hold and we obtain the assertion. Consider the mixed problem for an in finite system of parabolic equations where um=um(x,t)and Bk(x)are linear operators fromto lq(see[27,§1.18.2]for the definition of),and here Theorem 7.1Suppose thatBkare bounded operators fromandThen,forand forsufficiently largea>0,the problem(7.1)has a unique solutionthat belongstoand the following coercive uniform estimate holds: ProofReally,let E=lq,A be in finite matrices,defined by It is easy to see that the operator A is R-positive in lq.Therefore,all conditions of Theorem 5.1 hold and we obtain the assertion. [1]Ahmed,B.,Alsaedi,A.and Alghamidi,B.,Analytic approximation of solutions of the forced Duffing equation with integral boundary conditions,Nonlinear Anal.Real World Appl.,9,2008,1727–1740. [2]Amann,H.,Linear and Quasi-linear Equations,1,Birkhauser,Basel,1995. [3]Ashyralyev,A.,On well-posedness of the nonlocal boundary value problem for elliptic equations,Numerical Functional Analysis&Optimization,24(1–2),2003,1–15. [4]Besov,O.V.,Ilin,V.P.and Nikolskii,S.M.,Integral Representations of Functions and Embedding Theorems,Nauka,Moscow,1975. [5]Burkholder,D.L.,A geometrical conditions that implies the existence certain singular integral of Banach space-valued functions,Proc.Conf.Harmonic analysis in honor of Antonu Zigmund,Chicago,1981,Wads Worth,Belmont,1983,270–286. [6]Cannon,J.R.,Perez Esteva S.and van Der Hoek J.,A Galerkin procedure for the diffusion equation subject to the speci fication of mass,SIAM J.Numer.Anal.,24,1987,499–515. [7]Choi,Y.S.and Chan,K.Y.,A parabolic equation with nonlocal boundary conditions arising from electrochemistry,Nonlinear Anal.,18,1992,317–331. [8]Denk,R.,Hieber,M.and Prüss,J.,R-boundedness,Fourier multipliers and problems of elliptic and parabolic type,Mem.Amer.Math.Soc.,166,2003,788. [9]Dore,C.and Yakubov,S.,Semigroup estimates and non-coercive boundary value problems,Semigroup Forum.,60,2000,93–121. [10]Ewing,R.E.and Lin,T.,A class of parameter estimation techniques for fluid flow in porous media,Adv.Water Resour.,14,1991,89–97. [11]Favini,A.,Shakhmurov,V.and Yakubov,Y.,Regular boundary value problems for complete second order elliptic differential-operator equations in UMD Banach spaces,Semigroup Forum.,79(1),2009,22–54. [12]Goldstain,J.A.,Semigroups of Linear Operators and Applications,Oxfard University Press,Oxfard 1985. [13]Haller,R.,Heck,H.and Noll,A.,Mikhlin’s theorem for operator-valued Fourier multipliers in n variables,Math.Nachr.,244,2002,110–130. [14]Krein,S.G.,Linear Diff erential Equations in Banach Space,American Mathematical Society,Providence,1971. [15]Liang,J.,Nagel,R.and Xiao,T.J.,Approximation theorems for the propagators of higher order abstract Cauchy problems,Trans.Amer.Math.Soc.,360(4),2008,1723–1739. [16]Lions,J.L.and Magenes,E.,Nonhomogenous Boundary Value Problems,Mir,Moscow,1971. [17]Shahmurov,R.,Solution of the Dirichlet and Neumann problems for a modi fied Helmholtz equation in Besov spaces on an annuals,Journal of Diff erential Equations,249(3),2010,526–550. [18]Shakhmurov,V.B.,Imbedding theorems and their applications to degenerate equations,Diff erential Equations,24(4),1988,475–482. [19]Shakhmurov,V.B.,Coercive boundary value problems for regular degenerate differential-operator equations,J.Math.Anal.Appl.,292(2),2004,605–620. [20]Shakhmurov,V.B.,Embedding theorems and maximal regular differential operator equations in Banachvalued function spaces,Journal of Inequalities and Applications,2(4),2005,329–345. [21]Shakhmurov,V.B.,Embedding and maximal regular differential operators in Banach-valued weighted spaces,Acta Mathematica Sinica,22(5),2006,1493–1508. [22]Shakhmurov,V.B.,Linear and nonlinear abstract equations with parameters,Nonlinear Analysis,Method and Applications,73,2010,2383–2397. [23]Shi,P.and Shillor,M.,Design of contact patterns in one-dimensional thermoelasticity,Theoretical Aspects of Industrial Design,SIAM,Philadelphia,PA,1992. [24]Shklyar,A.Y.,Complete Second Order Linear Diff erential Equations in Hilbert Spaces,Birkhauser Verlak,Basel,1997. [25]Sobolevskii,P.E.,Coerciveness inequalities for abstract parabolic equations,Doklady Akademii Nauk SSSR,57(1),1964,27–40. [26]Triebel,H.,Interpolation Theory,Function Spaces,Diff erential Operators,North-Holland,Amsterdam,1978. [27]Weis,L.,Operator-valued Fourier multiplier theorems and maximal Lpregularity,Math.Ann.,319,2001,735–758. [28]Xiao,T.J.and Liang,J.,Second order differential operators with Feller-Wentzell type boundary conditions,J.Funct.Anal.,254,2008,1467–1486. [29]Xiao,T.J.and Liang,J.,Nonautonomous semilinear second order evolution equations with generalized Wentzell boundary conditions,J.Diff erential Equations,252,2012,3953–3971. [30]Yakubov,S.,Completeness of Root Functions of Regular Diff erential Operators,Longman,Scientific and Technical,New York,1994. [31]Yakubov,S.,A nonlocal boundary value problem for elliptic differential-operator equations and applications,Integr.Equ.Oper.Theory,35,1999,485–506. [32]Yakubov,S.and Yakubov,Y.,Diff erential-operator Equations,Ordinary and Partial Diff erential Equations,Chapman and Hall/CRC,Boca Raton,2000.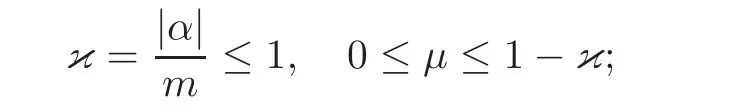
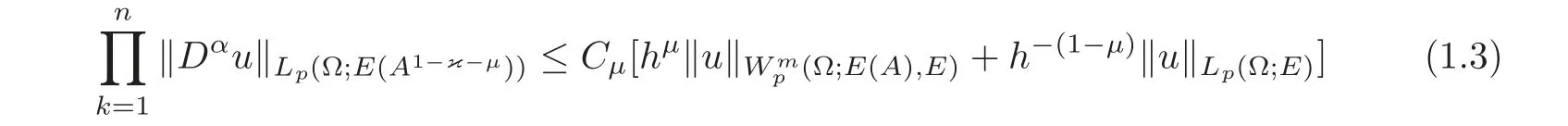
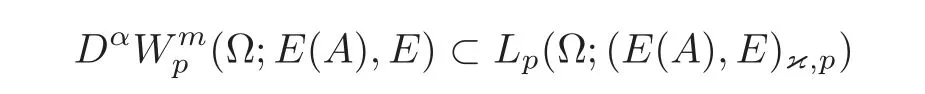
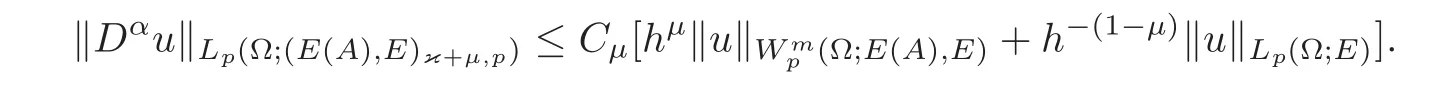
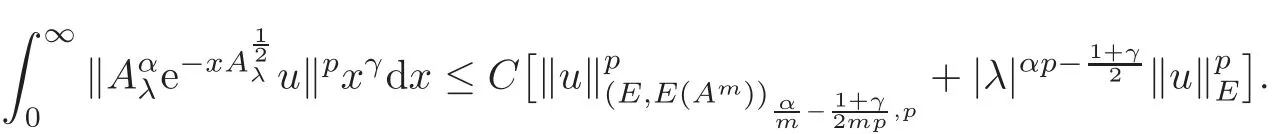
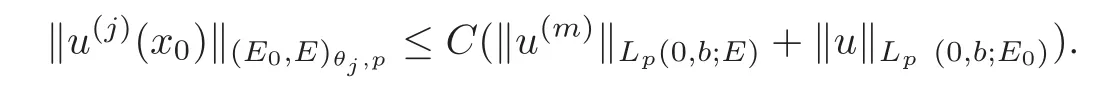
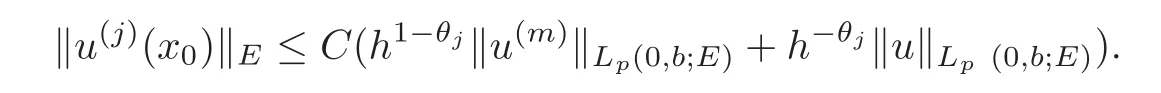

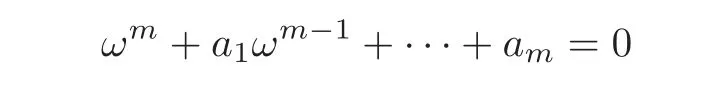
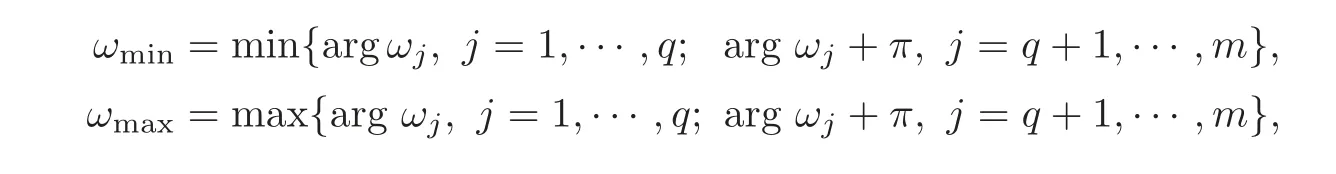
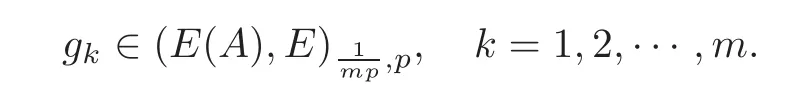
2 Statement of the Problem
3 Homogeneous Equations


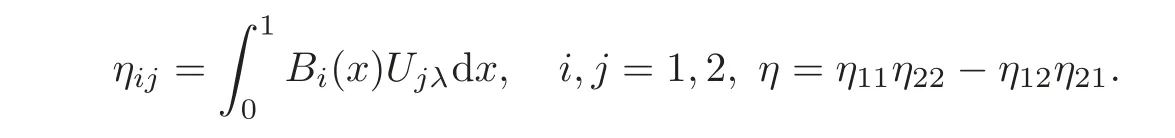
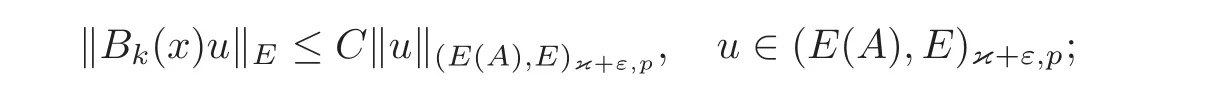
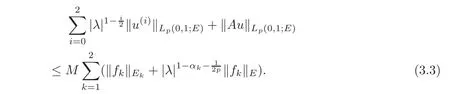
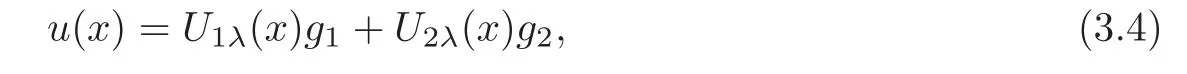
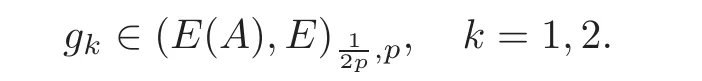
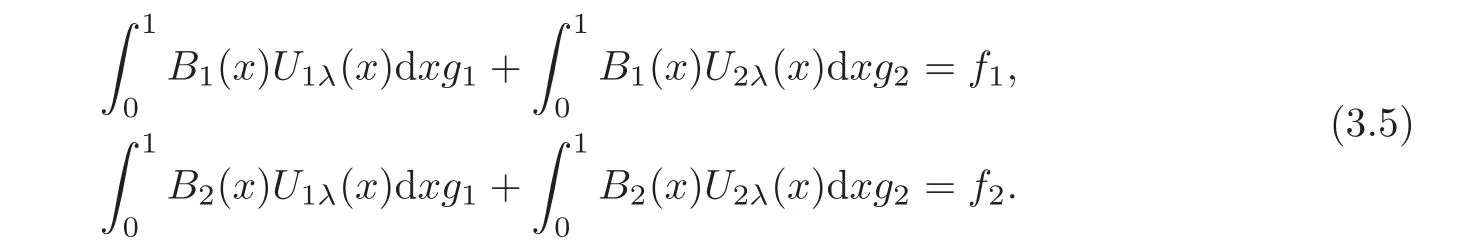
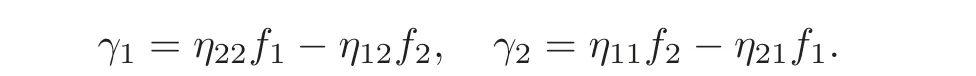
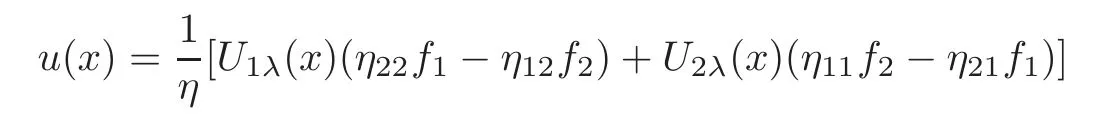

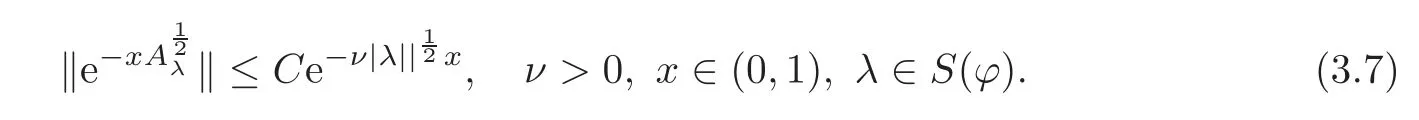
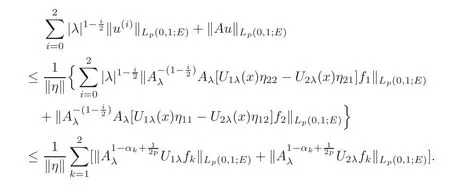
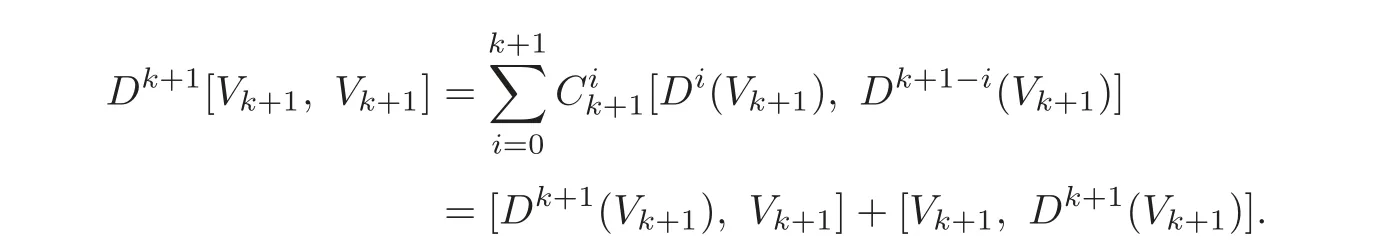
4 Non-homogenous Equations
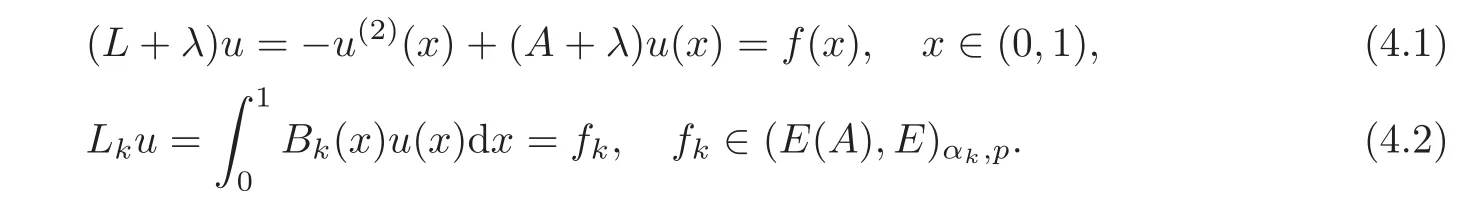
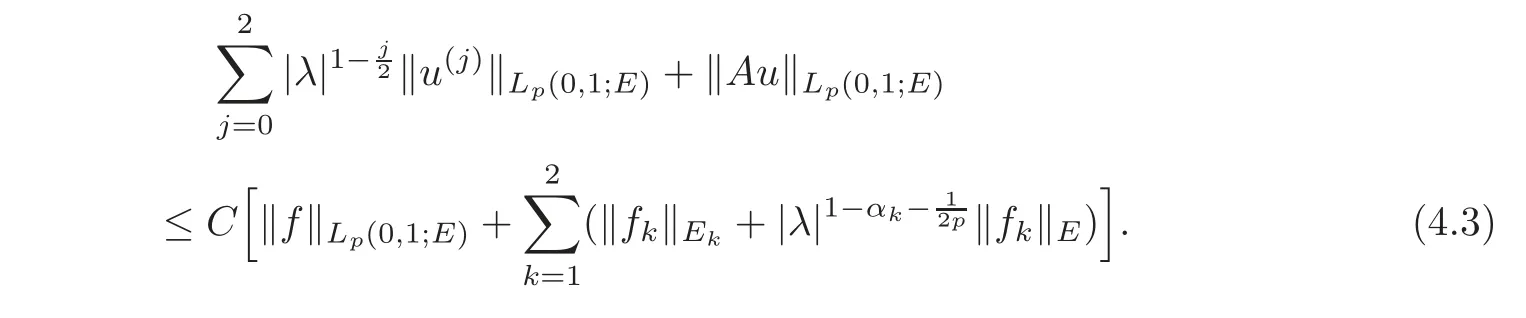
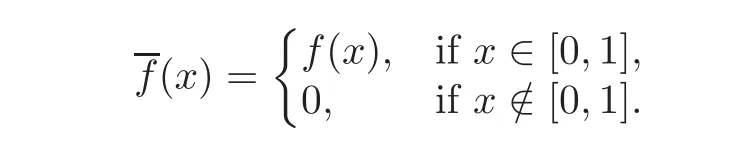
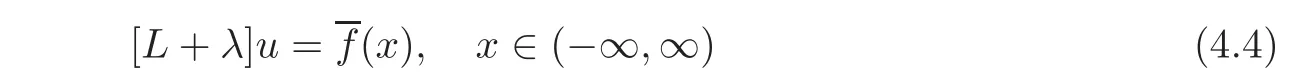
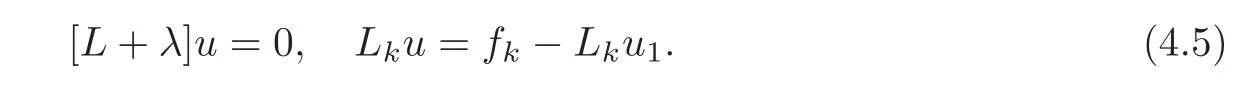
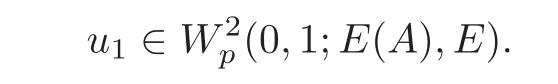
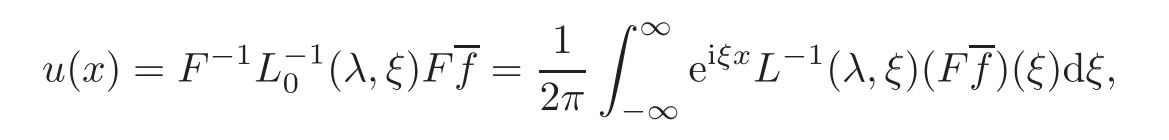
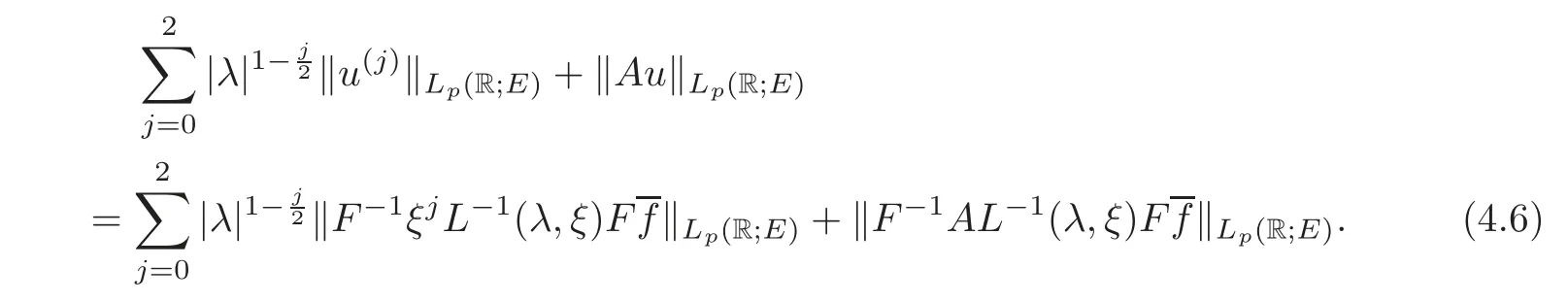
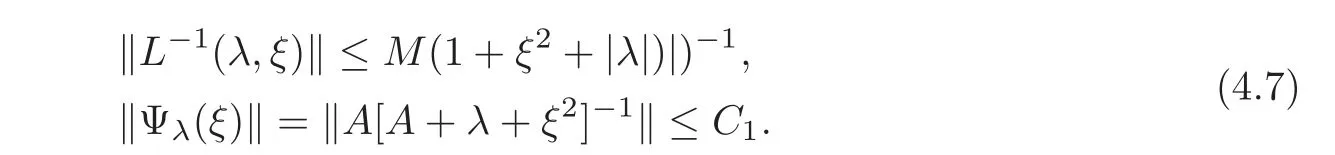
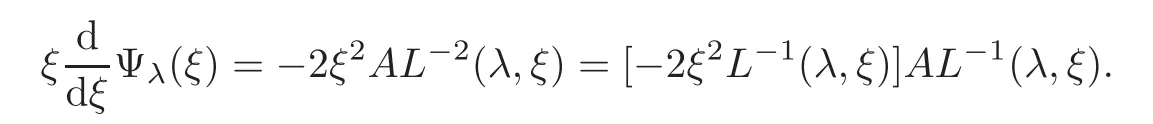
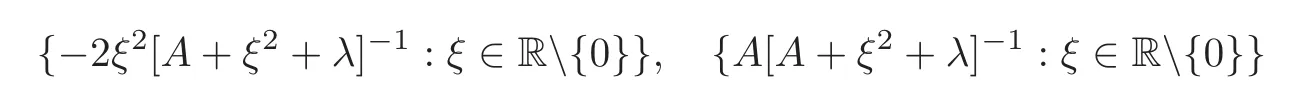
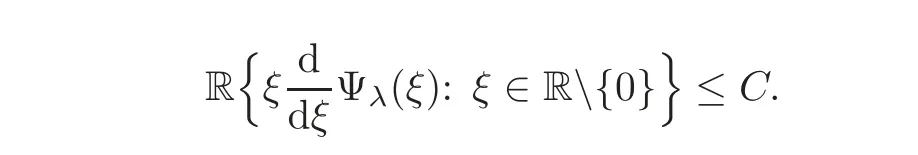
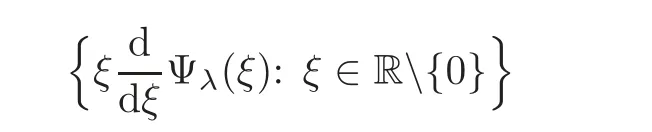
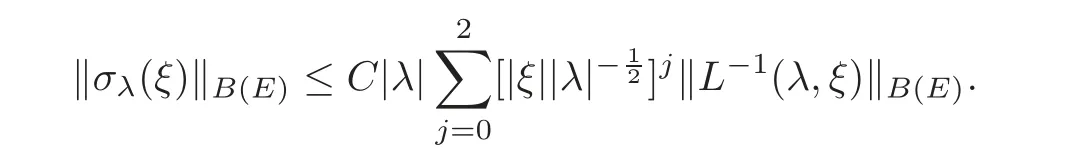
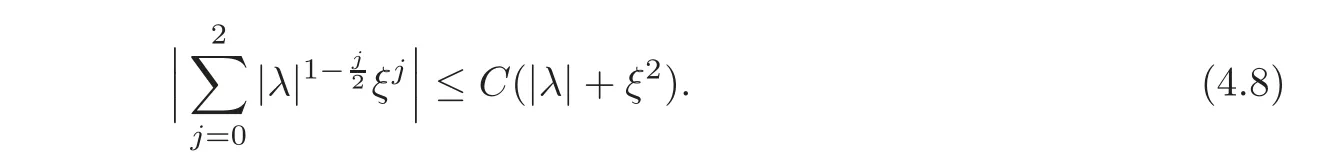
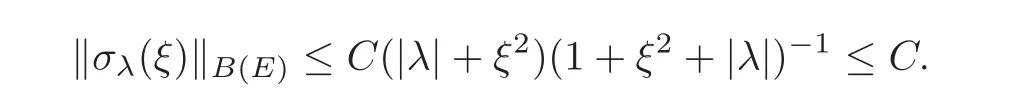
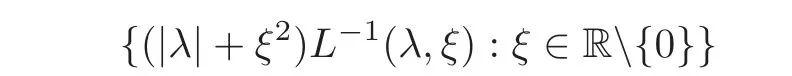
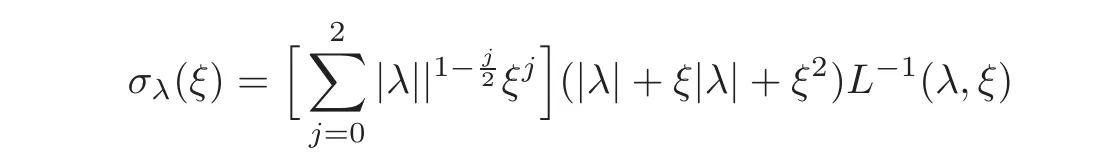
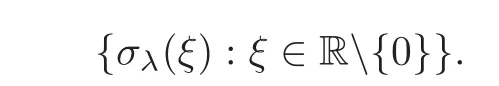
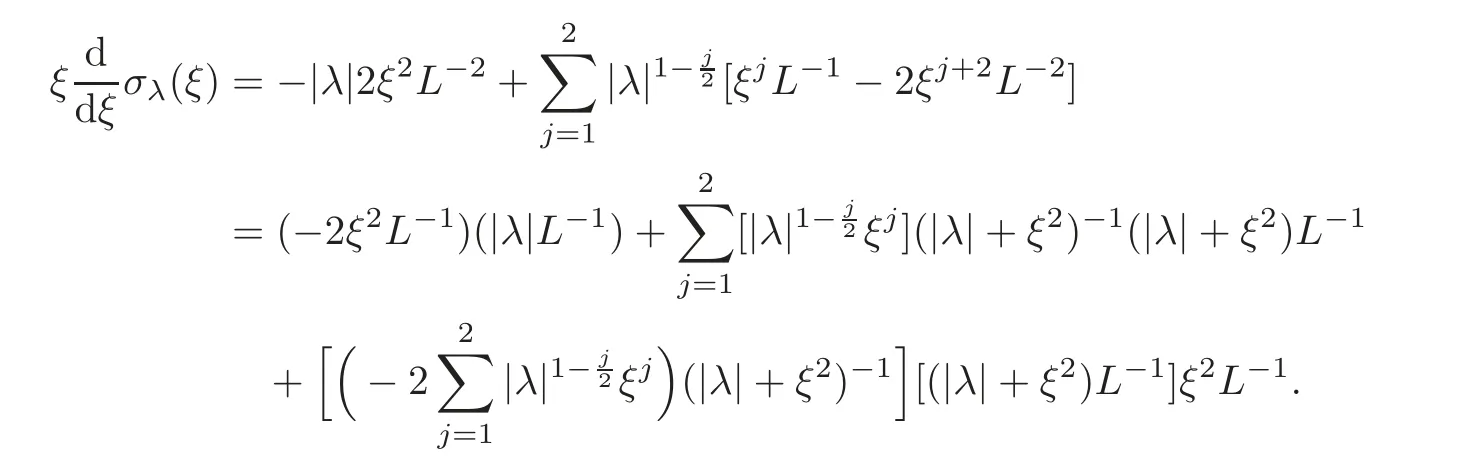
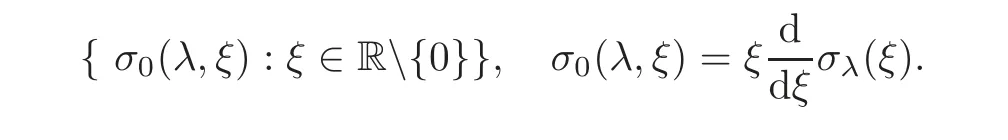
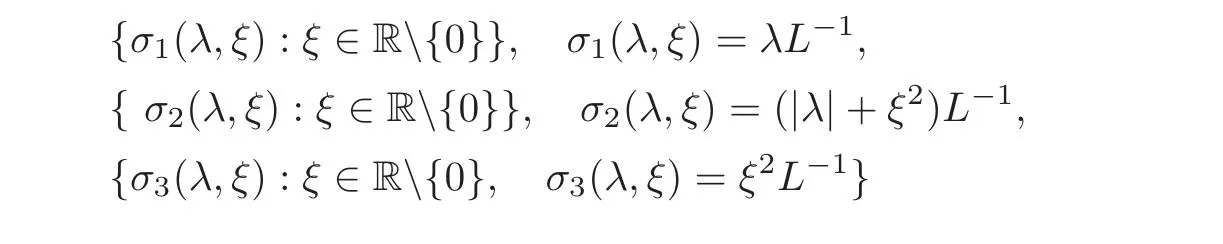
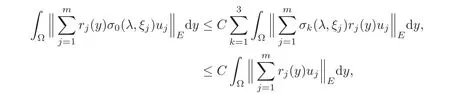

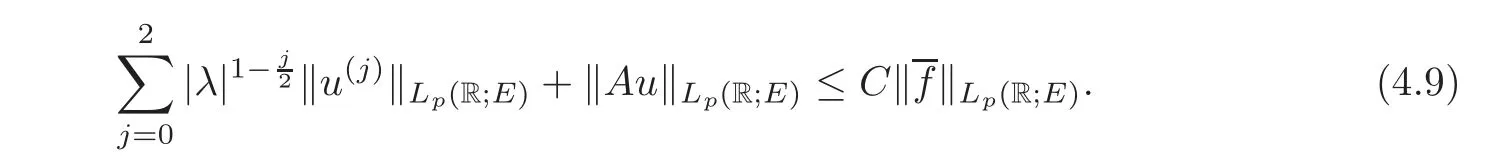
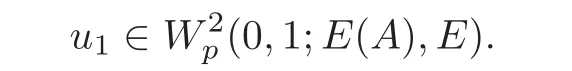
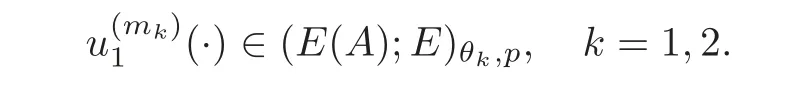
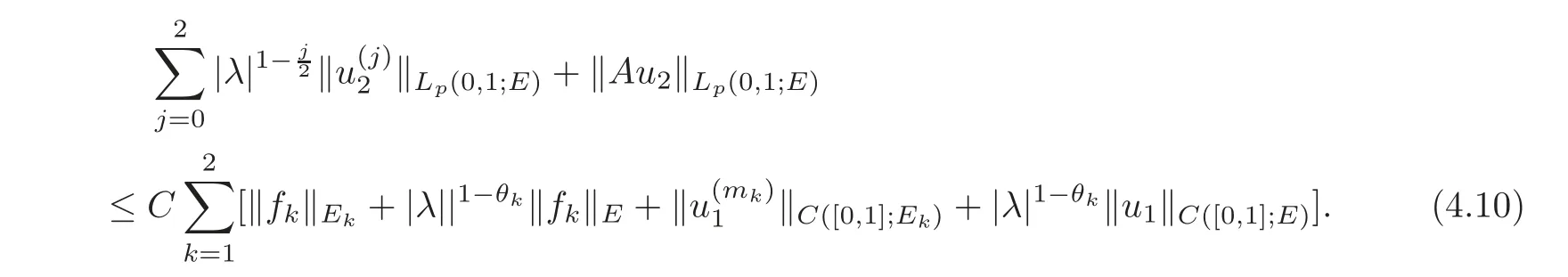
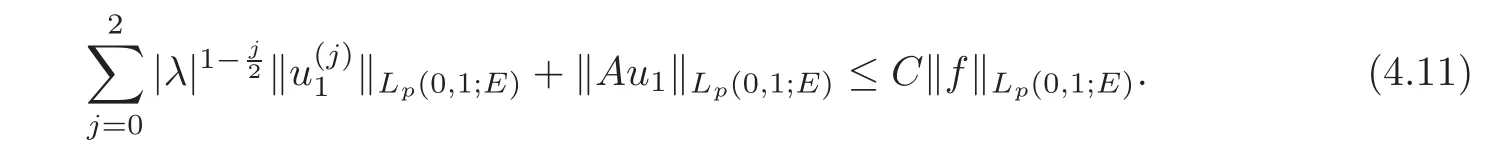
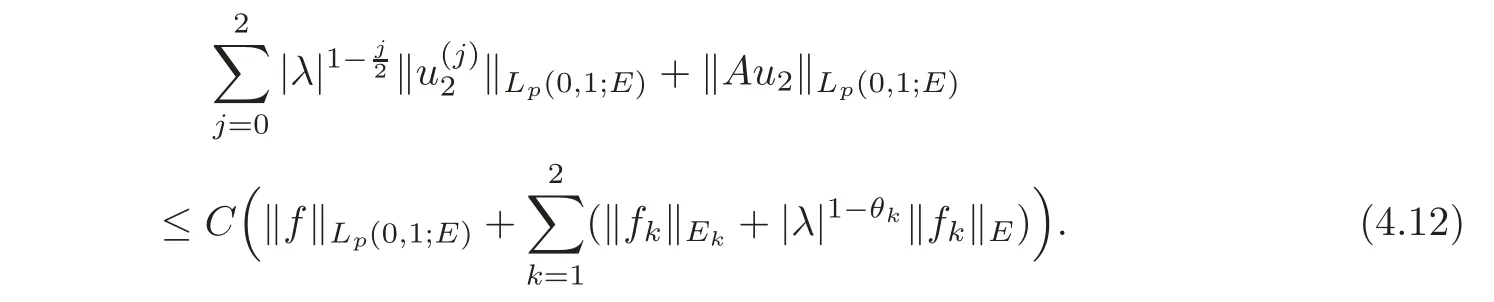
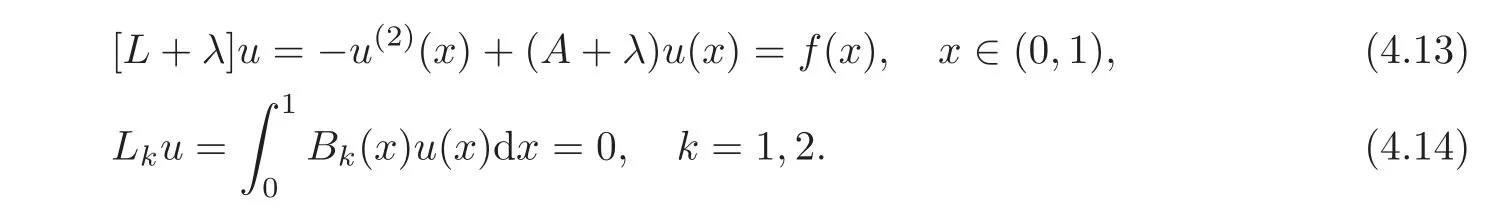
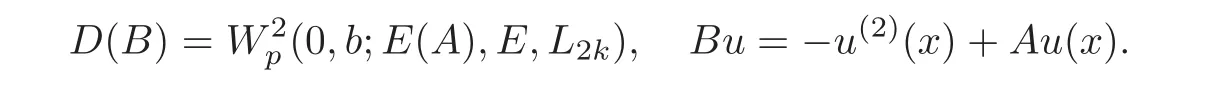
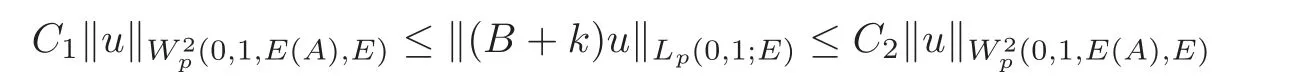
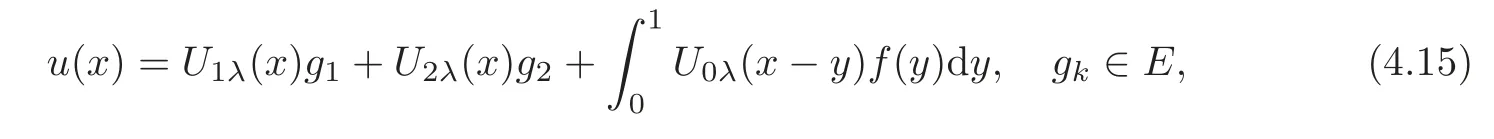
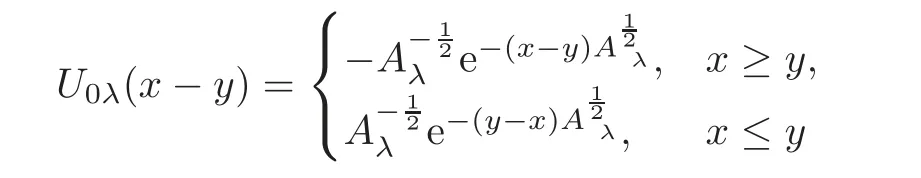
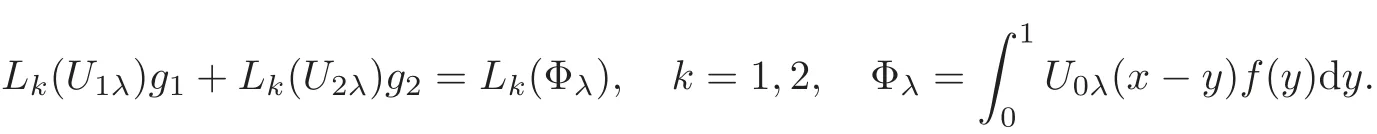
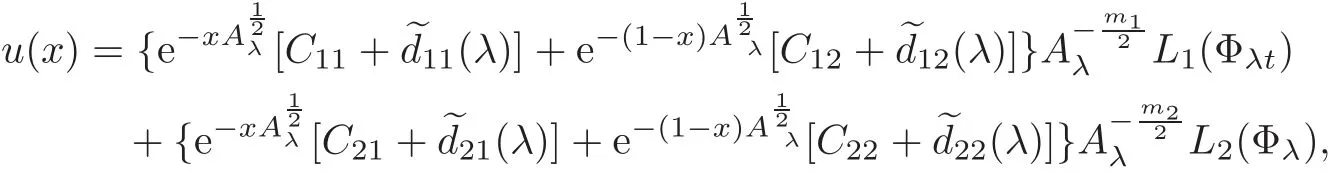

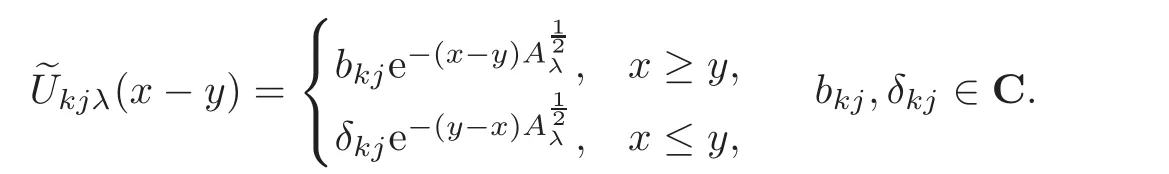
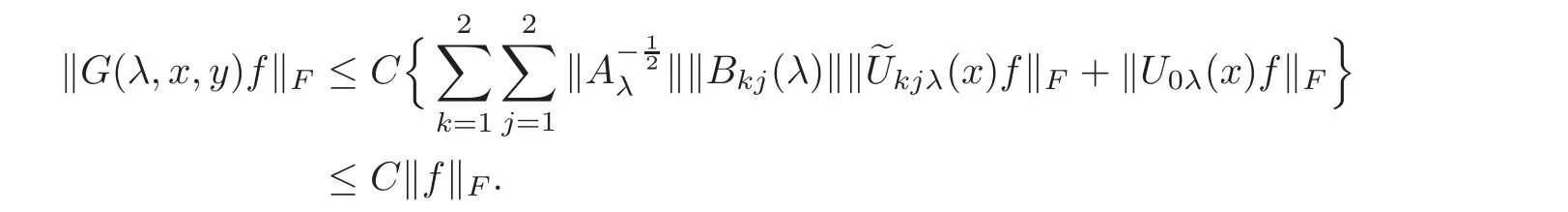
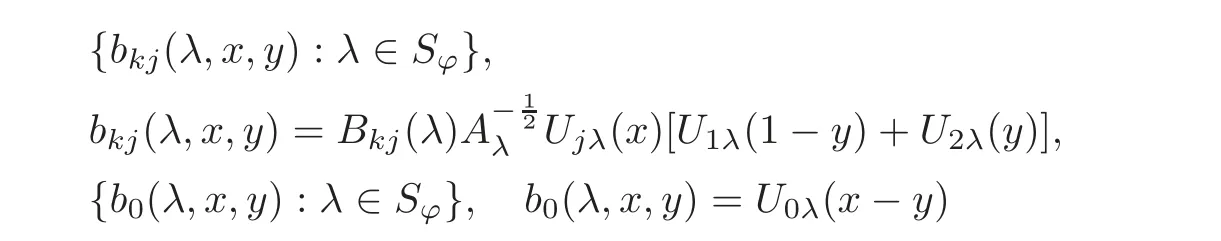

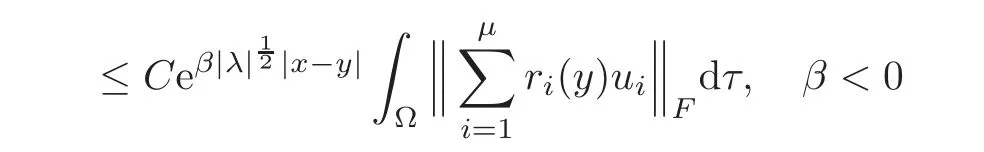
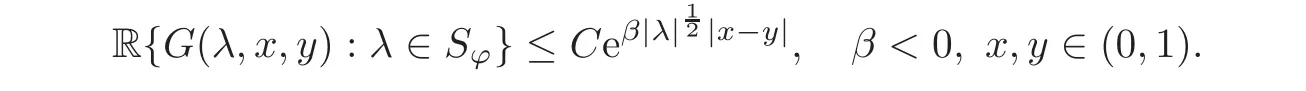
5 Cauchy Problem for Abstract Parabolic Equation
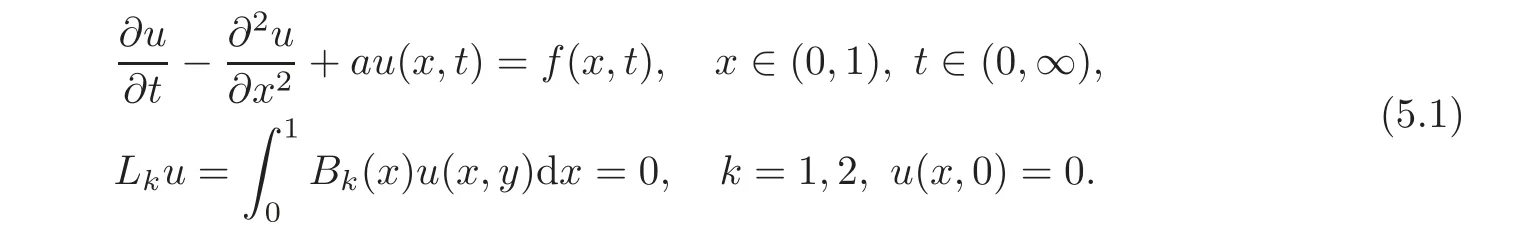

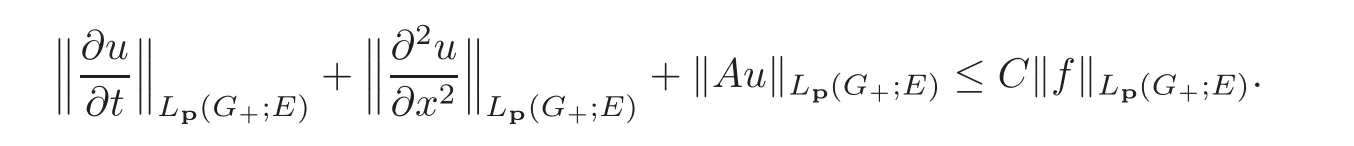


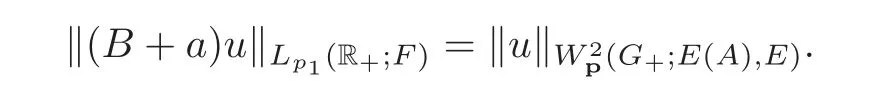
6 Nonlocal Boundary Value Problems for Elliptic Equations

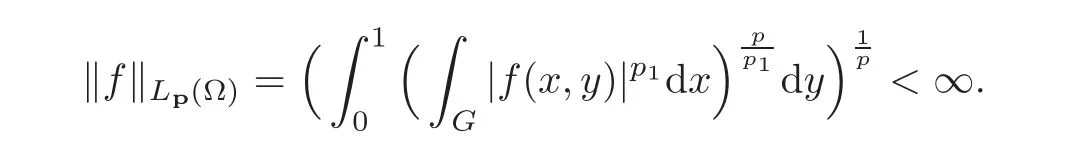
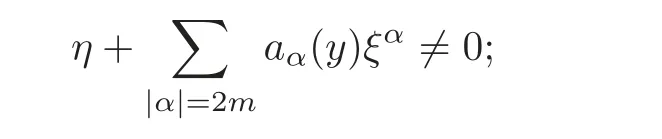
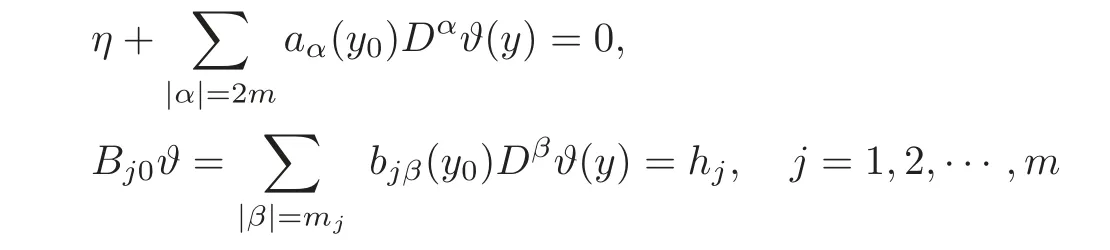
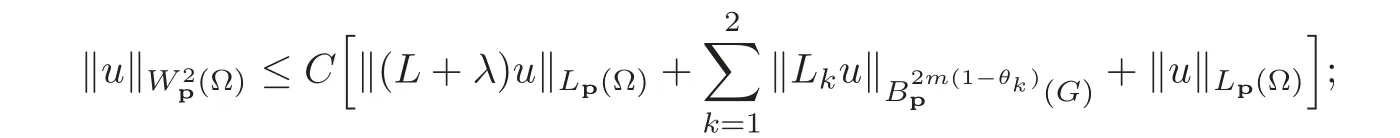
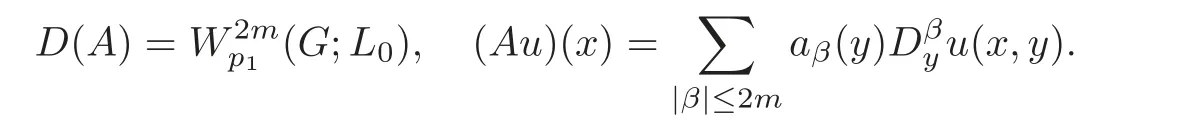

7 In finite Systems of Parabolic Equations

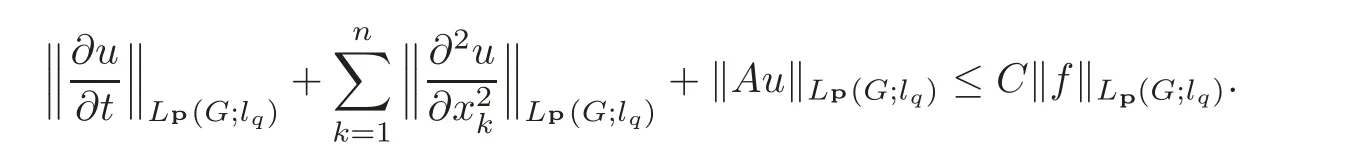
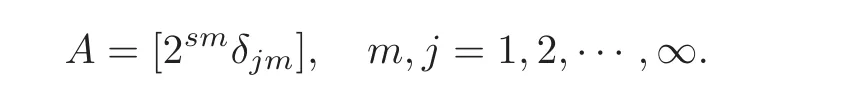
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Cohen-Fischman-Westreich’s Double Centralizer Theorem for Almost-Triangular Hopf Algebras∗
- Recognizing the Automorphism Groups of Mathieu Groups Through Their Orders and Large Degrees of Their Irreducible Characters∗
- Exact Controllability with Internal Controls for First-Order Quasilinear Hyperbolic Systems with Zero Eigenvalues
- On the GF(p)Linear Complexity of Hall’s Sextic Sequences and Some Cyclotomic-Set-Based Sequences∗
- Geometrical Realization of Low-Dimensional Complete Intersections∗
- Positivity of Fock Toeplitz Operators via the Berezin Transform∗
