Order Bounded Weighted Composition Operators Mapping into the Dirichlet Type Spaces∗
2016-05-28YongxinGAOSanjayKUMARZehuaZHOU
Yongxin GAOSanjay KUMARZehua ZHOU
1 Introduction
Let D be the open unit disk in the complex plane C,and H(D)denote the space of analytic functions on D.Suppose that ϕ and h are analytic functions defined on D such that ϕ(D) ⊆ D.The weighted composition operator Wh,ϕis defined as
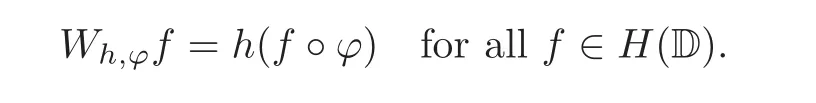
When ϕ is identity on D,the operator is the multiplication operator Mh.When h ≡ 1,it is the composition operator Cϕ.
Weighted composition operators are general class of operators and they appear naturally in the study of surjective isometries on most of the function spaces,semigroup theory,dynamical systems,Brennan’s conjecture,etc.Recently,there has been an increasing interest in studying weighted composition operators acting on different spaces of analytic functions(see[1–3,12,16–17,20–22]and the references therein).
Let X be a Banach space of analytic functions in D and let q>0.Let μ be a positive Borel measure on the unit circle.The operator T:X → Lq(μ)is said to be order bounded if there exists h∈Lq(μ),h≥0 such that for each f∈X with
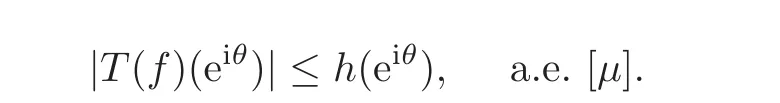
In particular,let ϕ be an analytic self-map of D such that ϕ∗∈ Lpβ,p ≥ 1, β >0.In[10],H.Hunziker characterized the self-maps ϕ of the unit disk for which the composition operator Cϕ:Hp→ Lpβis order bounded.In this context,Cϕf is supposed the boundary function(f ◦ ϕ)∗.
In this paper,we focus on weighted composition operators acting on the Dirichlet type spaces.In contrast,the Dirichlet type spaces include functions that have no boundary values.Thus a discussion of order bounded weighted composition operators on Dirichlet type spaces will require the assumption thatwith respect to the normalized Lebesgue measure m.The composition operator Cϕon Hardy space or weighted Bergman spaces was investigated in[4].Within setting of composition operators the order boundedness is connected with the boundedness or the compactness of them.For instance,H.Hunziker and H.Jarchow[11]proved that for β ≥ 1,the order boundedness of Cϕ:Hp→ Lβp(∂D,m)implies the compactness of Cϕ:Hp→ Lβp,where m is the normalized Lebesgue measure on the unit circle∂D.So the order boundedness is also an interesting subject in the study of composition operators.R.A.Hibschweiler[9]studied the order bounded weighted composition operators mapping into Lβp(∂D,m).Recently Ueki[18]has studied the order boundedness of weighted composition operators on Bergman spaces.In this article,we characterize the order bounedeness of weighted composition operators on Dirichlet type spaces.
Recall that for 1≤p<∞,the classical Hardy space Hpconsists of analytic functions f on D,for which the norm

If p=∞,H∞is the space of analytic functions f on D such that
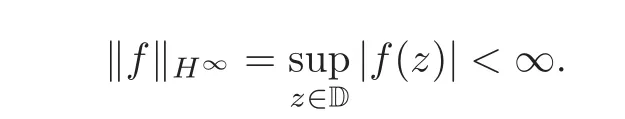
Fatou’s theorem asserts that any Hardy function f has radial limit at eiθ∈ ∂D except on a set Lebesgue measure zero.Throughout this work,f(eiθ)will denote the radial limit of f at eiθ,denote the normalised Lebesgue area measure on D.Also,let dAα(z)=(1+α)(1−|z|2)αdA(z)denote the weighted Lebesgue area measure on D,where−1<α<∞.For 0 If α=0,we get the Bergman space For 0 That is,f∈if and only if f'∈.For α=0,the spacesis the classical Dirichlet space.For other values of p and α,the spaceshave been extensively studied in number of papers(see[6–7,15,19]).The spacesare called Dirichlet spaces if p≥ α+1.For α=0,the spaceis the classical Dirichlet space.If p<α+1,then it is well known that=(see[5,Theorem 6]).Alsoequals to the Hardy spaces H2.Further,if 1≤q and and the inclusions are strict when p2.The inclusion(1.1)for 1≤p≤2 can be proved by Riesz-Thorin Theorem and the case 0 for almost every point eitin the Fatou set of f,Ff,which consists of those eiθ∈ T such that f has a finite non-tangential limit at eiθ.Then obviously,(1.3)implies An analytic function f on D is said to belong to the Bloch-type space Bβ(D)=Bβif The expression B(f)defines a semi-norm while a natural norm is given byB(f).It makes Bβinto a Banach space. In this section,we characterize the order boundedness of weighted composition operators Wh,ϕacting between Dirichlet type spaces.Before formulating and proving the results,we first give some auxiliary results. For any 0 We also have the following lemma. Lemma 2.1Supposec>−1andd≥0.Let Then we have the following asymptotic properties: (1)Ifd>0,then (2)Ifd=0,then Now we can prove the following lemma. Lemma 2.2For0 ProofBy the equation(2.1),we have where C2depends only on α and p and f∈.This yields the second inequality.For the remaining inequality,let Then by using Lemma 2.1,we can find C1>0 such that.Therefore, The next theorem is our first equivalent condition of the order boundedness of Wh,ϕacting on Theorem 2.1Suppose0 (i)is order bounded; (ii) ProofSuppose thatSincea.e.[m],then by Lemma 2.2,there is a constant C depending only on p and α such thata.e.[m]for all f withLet Then clearly t ∈ Lq(m)by hypothesis and previous inequality implies thatt(eiθ)a.e.[m].Thus Wh,ϕ:→Lq(m)is order bounded. Next suppose that Wh,ϕ:→Lq(m)is order bounded.Then there exists t∈Lq(m),t≥0 witha.e.[m]for all f withThus by Lemma 2.2,the inequality It follows that Remark 2.1It is easy to check that under the condition of Theorem 2.1, if and only if Even though the requirements in Theorem 2.1 seem strong,the result is still usefulin many nontrivial cases. Example 2.1LetandThen Thus we can know that the composition operator Cϕis not order bounded frominto L1(m).However,the behavior of h near the point 1 guarantees that so Wh,ϕis order bounded frominto L1(m),with the help of the weight h. On the other hand,if we takethen even though with the same weight h,Wh, ϕis no longer order bounded frominto L1(m). In fact,this example shows that the order boundedness of Wh,ϕis determined by h and ϕ together in the way we show in Theorem 2.1. Corollary 2.1Suppose0 (i)Wh,ϕ:→Lq(m)is order bounded; (ii)Wh,ϕn:→Lq(m)is order bounded for somen∈N∗; (iii)Wh,ϕn:→Lq(m)is order bounded for eachn∈N∗; ProofBy using Theorem 2.1 and the inequality that we get the desired result. Remark 2.2Suppose that h∈L∞,ϕ is an analytic self-map of the unit disk such thatandis order bounded for some α>−1.By Theorem 2.1,If we can even require α +1>p,then it follows that Thus Now if α=p−2,then=Bp,the Besov space.Whenever f∈,for α=p−2,α>−1 and 1 Moreover,we have the following lemma. Lemma 2.3Let0 ProofThe existence of C2follows directly from(2.2).Now take Then by using Lemma 2.1,we can find C1>0 such thatTherefore,we obtain The proof of the following theorem is almost similar to Theorem 2.1,so we omit the details. Theorem 2.2Suppose0 (i)Wh,ϕ:→Lq(m)is order bounded; (ii) Now let’s turn to the Hardy and Bergman spaces.We also begin with the following well known lemma. Lemma 2.4Suppose0 and Again,by imitating the proof of Theorem 2.1,we get the following equivalent conditions. Theorem 2.3Suppose0 (i)Wh,ϕ:Hp→Lq(m)is order bounded; (ii)Wh,ϕ:A2p→Lq(m)is order bounded; (iii) Finally in this section,we give the following results as corollaries of Theorems 2.1–2.3. Corollary 2.2Suppose0 Corollary 2.3Fix0 (i)Wh,ϕ:→ Lq(m)is order bounded; (ii) In this section,we characterize the order boundedness of weighted composition operators Wh,ϕacting between Dirichlet type spaces.Recall that in this case,Wh,ϕis order bounded if and only if we can find g∈ Lq(Aq−1),g≥ 0 such that for allwe have The proof of the following lemma follows similar lines as the proof of Lemma 3.2 of[8].So we omit the proof. Lemma 3.1Let0 (i)sup{|f(z)|: (ii)sup{|f'(z)|: Theorem 3.1Let0 thenWh,ϕ:is bounded. ProofLetand z∈ D.Then by Lemma 3.1,we have Therefore, Combining this with the assumption,we get the desired result. Corollary 3.1Let0 ProofSuppose that condition(3.1)is true and take a functionwithIt follows from Theorem 3.1 thatis bounded.Moreover,as in the proof of Theorem 3.1,we see that Lemma 3.1 gives TakeThe condition(3.1)implies thatand g ≥ 0.That is,the weighted composition operatoris order bounded. Theorem 3.2Let0 ProofSince Wh,ϕ:is order bounded,there exists a non-negative function g ∈ Lqsuch thatfor all z ∈ D and for allwithFix a.e.z∈D.Let Then So by taking w=z,we can get Then the result follows directly since g∈Lq. AcknowledgementsThe authors would like to thank the referee for usefulcomments and suggestions which helped to improve the presentation of this paper.The second author is extremely thankfulto Professor Daniel Girela for the kind suggestions. [1]Cheng,Y.,Kumar,S.and Zhou,Z.H.,Weighted composition operators on Dirichlet-type spaces and related Qpspaces,Publ.Math.Debrecen,80,2012,79–88. [2]Contreras,M.D.and Hern´andez-D´ıaz,A.G.,Weighted composition operators on Hardy spaces,J.Math.Anal.Appl.,263,2001,224–233. [3]ukovi,.and Zhao,R.,Weighted composition operators on the Bergman spaces,J.London Math.Soc.,70,2004,499–511. [4]Domenig,T.,Order bounded and p-summing composition operators,Contemp.Math.,213,1998,27–41. [5]Flett,T.M.,The dual of an inequality of Hardy and Littlewood and some related inequalities,J.Math.Anal.Appl.,38,1972,756–765. [6]Girela,D.and Pelez,J.A.,Carleson measures,multipliers and integration operators for spaces of Dirichlet type,J.Funct.Anal.,214,2006,334–358. [7]Girela,D.and Pelez,J.A.,Growth properties and sequences of zeros of analytic functions in spaces of Dirichlet type,J.Aust.Math.Soc.,80,2006,397–418. [8]Hedenmalm,H.,Korenblum,B.and Zhu,K.,Theory of Bergman Spaces,Springer-Verlag,New York,2000. [9]Hibschweiler,R.A.,Order bounded weighted composition operators,Contemp.Math.,454,2008,93–105. [10]Hunziker,H.,Kompositions operatoren auf klassichen Hardyraumen,Universitat Zurich,1989. [11]Hunziker,H.and Jarchow,H.,Composition operators which improve integrability,Math.Nachr.,152,1991,83–99. [12]Kumar,S.,Weighted composition operators between spaces of Dirichlet type,Rev.Mat.Complut.,22,2009,469–488. [13]Littlewood,J.E.and Paley,R.E.A.C.,Theorems on Fourier series and power series II,Proc.London Math.Soc.,42,1936,52–89. [14]Luecking,D.H.,Multipliers of Bergman spaces into Lebesgue spaces,Proc.Edinburgh Math.Soc.,29,1986,125–131. [15]Rochberg,R.and Wu,Z.,Toeplitz operators on Dirichlet spaces,Integr.Equ.Oper.Theory,15,1992,57–75. [16]Smith,W.,Brennan’s conjecture for weighted composition operators,Recent Advances in Operator-Related Function theory,Centemp.Math.,Amer.Math.Soc.,393,2005,201–214. [17]Song,X.J.and Zhou,Z.H.,Diff erences of weighted composition operators from Bloch space to H∞on the unit ball,J.Math.Anal.Appl.,401,2013,447–457. [18]Ueki,S.,Order bounded weighted composition operators mapping into the Bergman space,Complex Anal.Oper.Theory,6,2012,549–560. [19]Wu,Z.,Carleson measures and multipliers for Dirichlet spaces,J.Funct.Anal.,169,1999,148–163. [20]Zhang,L.and Zhou,Z.H.,Hypercyclicity of weighted composition operator on weighted Dirichlet space,Complex Var.Elliptic Equ.,59,2014,1043–1051. [21]Zhou,Z.H.and Chen,R.Y.,Weighted composition operator from F(p,q,s)space to the Bloch type spaces on the unit ball,Internat.J.Math.,19,2008,899–926. [22]Zhou,Z.H.,Liang,Y.X.and Zeng,H.G.,Essential norms of weighted composition operators from weighted Bergman space to mixed-norm space on the unit ball,Acta Math.Sin.(Engl.Ser.),29,2013,547–556. [23]Zygmund,A.,On certain integrals,Trans.Am.Math.Soc.,55,1944,170–204.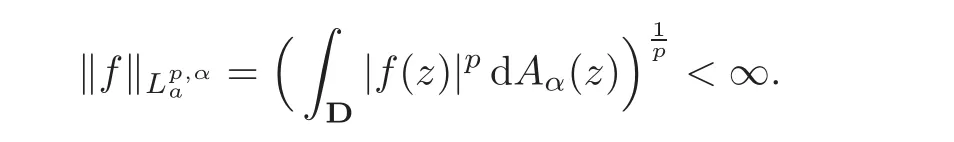
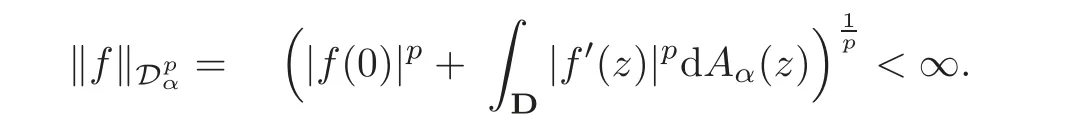


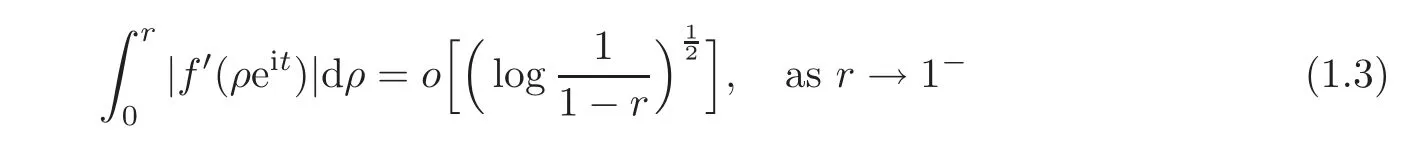
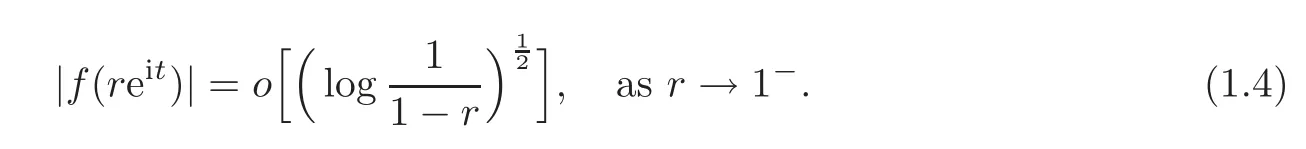
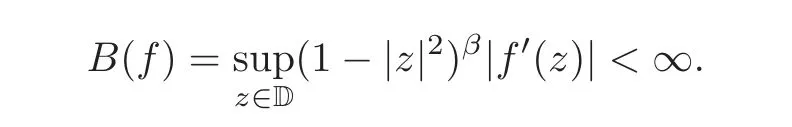
2 Order Boundedness
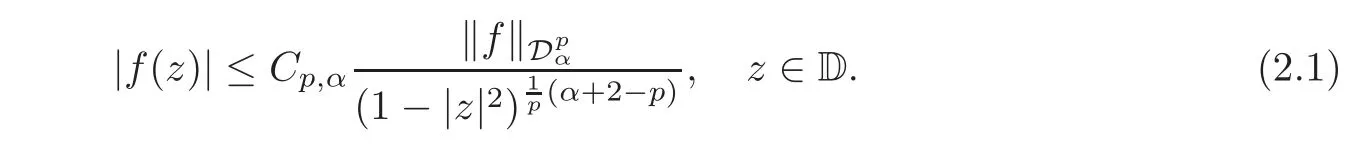
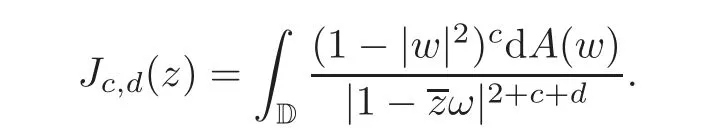
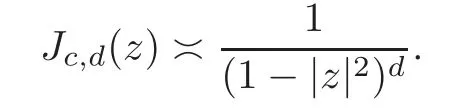
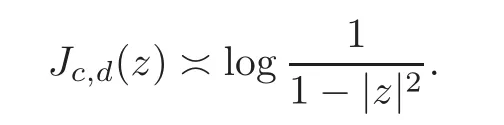
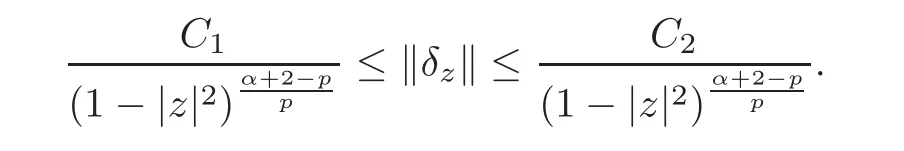



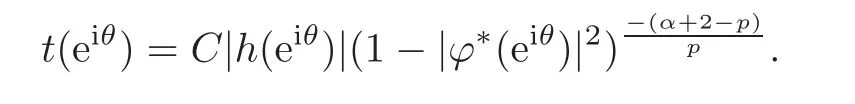
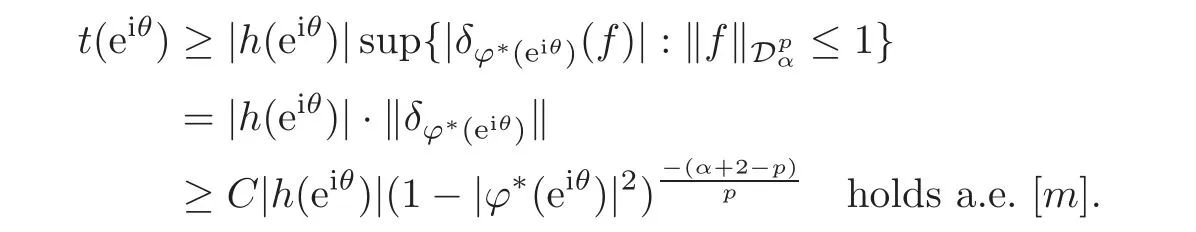
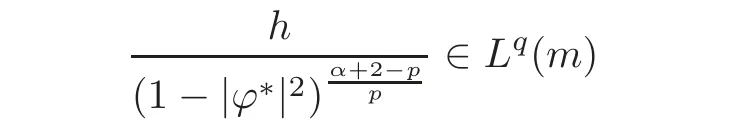

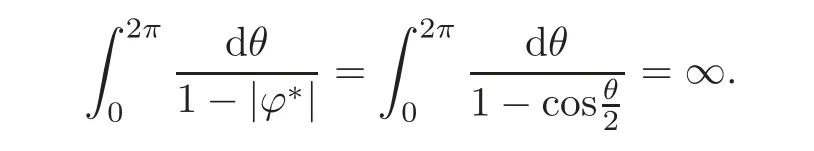
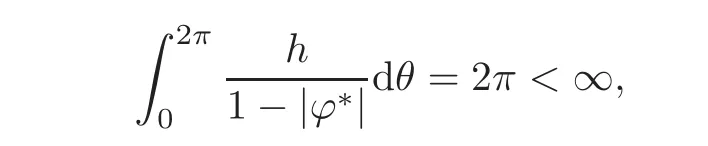
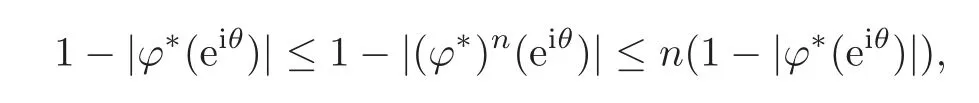

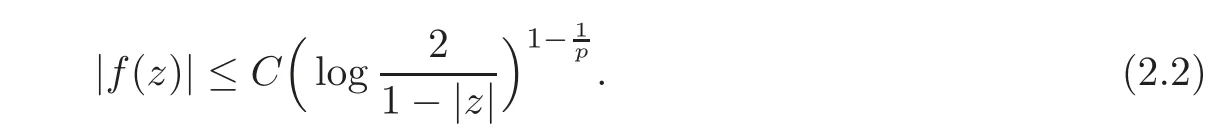
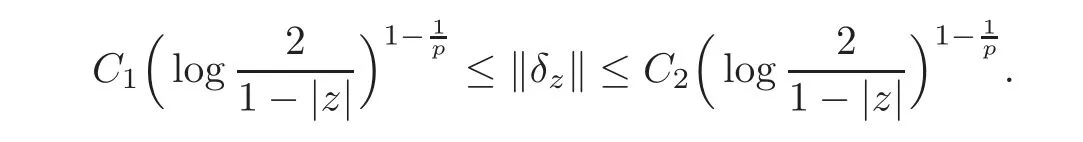
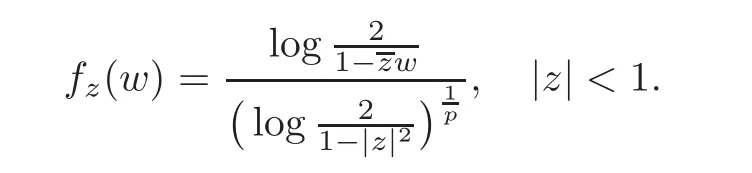
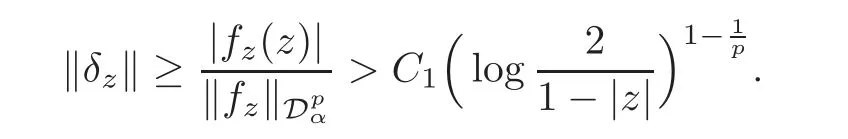

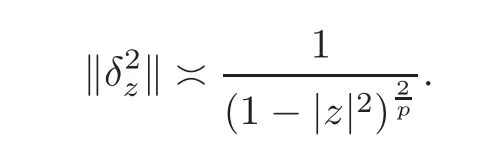
3 Order Boundedness of Wh,ϕ : →


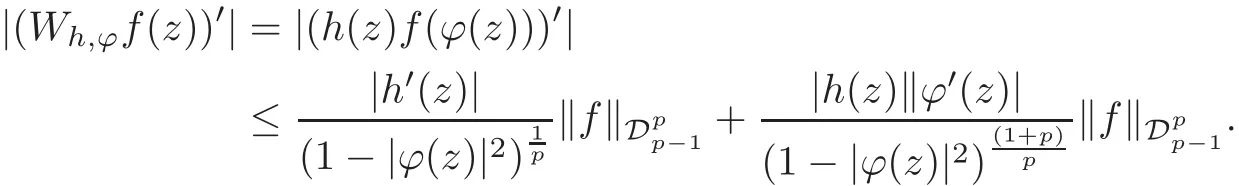
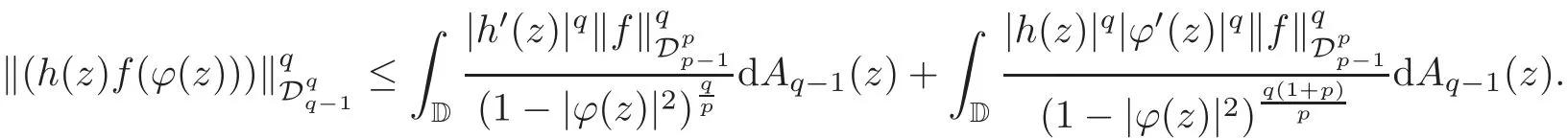
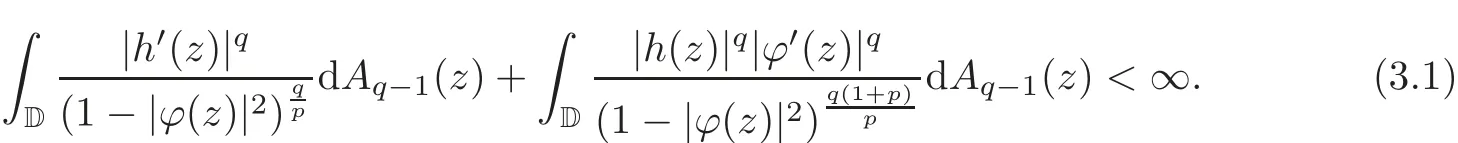
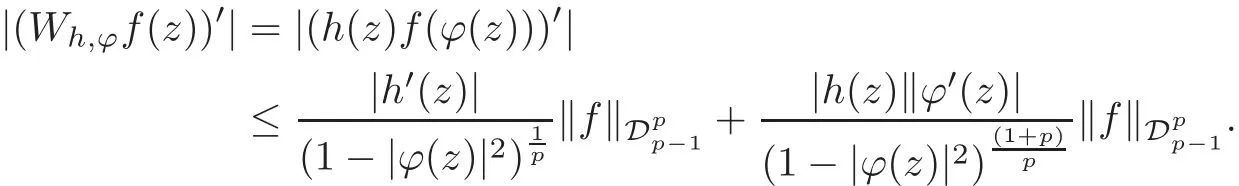
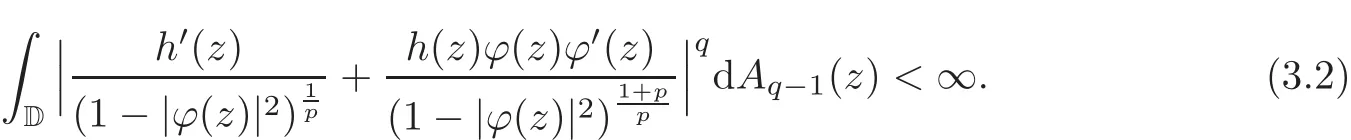
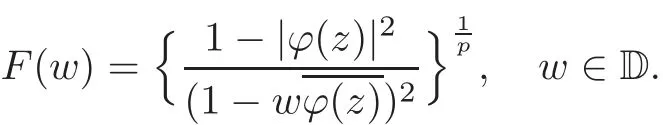
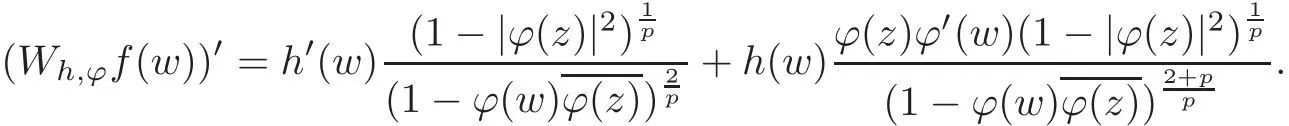
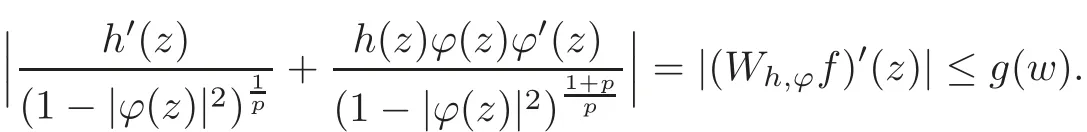
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Cohen-Fischman-Westreich’s Double Centralizer Theorem for Almost-Triangular Hopf Algebras∗
- Recognizing the Automorphism Groups of Mathieu Groups Through Their Orders and Large Degrees of Their Irreducible Characters∗
- Exact Controllability with Internal Controls for First-Order Quasilinear Hyperbolic Systems with Zero Eigenvalues
- On the GF(p)Linear Complexity of Hall’s Sextic Sequences and Some Cyclotomic-Set-Based Sequences∗
- Geometrical Realization of Low-Dimensional Complete Intersections∗
- Positivity of Fock Toeplitz Operators via the Berezin Transform∗
