Augmentation Quotients for Complex Representation Rings of Generalized Quaternion Groups∗

Shan CHANG

1 Introduction

Let G be a finite group.A complex matrix representation(for convenience,we use“representation”in the sequel)of G is a group homomorphism

where GLd(C)is the complex general linear group of rank d(d∈N).We also say that d is the degree of ρ(here we set GL0(C)to be the trivial group consisting of the empty matrix).Two representations ρ and η are said to be similar(denoted by ρ ∼ η),if there exists an invertible square matrix P such that

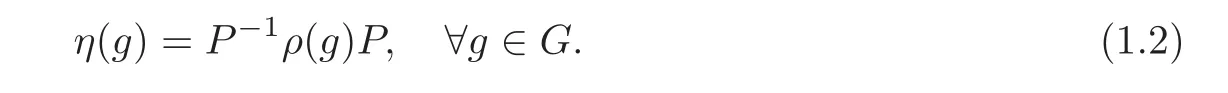
It is easy to see that similarity of representations is an equivalence relation.The equivalence classes are called similarity classes.The similarity class of ρ is denoted byThe direct sumof two similarity classesandis defined bywhere

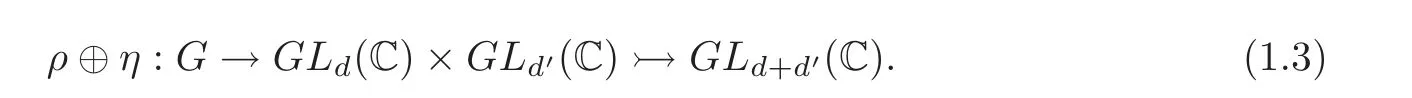
The complex representation ring R(G)is the group completion of the monoid(under direct sum⊕)of similarity classes of representations of G.Its addition and multiplication are induced by the direct sum and the tensor product of matrices,respectively.By[1],R(G)is a commutative ring with an identity element.Its underlying group is a finitely generated free abelian group with a basis consists of the similarity classes of irreducible representations.Hence,by[2],its free rank is equal to the number of conjugacy classes of G.

The notion of degree of a representation induces a ring homomorphism

This homomorphism is called the augmentation map.Its kernel Δ(G)is called the augmentation ideal of R(G).Let Δn(G)and Qn(G)denote the n-th power of Δ(G)and the n-th consecutive quotient group,respectively.

It is an interesting problem to determine the structures of Δn(G)and Qn(G)since they have many connections with other algebraic branches.The problem has been tackled in some papers[3–5].In particular,the author and the collaborators proved in[3]that,for any finite abelian group G,

where I is the augmentation ideal of the integral group ring ZG.Karpilovsky raised the problem of determining the isomorphism type of the groupsin[6].The author and Tang Guoping solved it in[7]and thereby solved the problem for the groups Qn(G).

The goal of this article is to give an explicit Z-basis for each Δn(Qm)and determine the isomorphism class of each Qn(Qm)for each positive integer n,where Qmis the generalized quaternion group of order 4m,m?2.

The result also computesbecause for any finite group G,Qn(G)

2 Preliminaries

In this section,we provide some usefulresults about Qn(G)and the finite generated free abelian groups.

The following theorem and corollary(proved in[3])are simple but useful.

Theorem 2.1(cf.[3])For any natural numbern,Qn(G)is a finite abelian|G|-torsion group.

Corollary 2.1(cf.[3])For each positive integern,Δn(G)has free rankc(G)−1,wherec(G)is the number of conjugacy classes ofG.

It is well known that any two representations with the same character are similar.Moreover,there is an injective ring homomorphism

which sends ρ to its character χρfor each representation ρ of G.

At last,we recall a classical result about the finite generated free abelian groups.

Lemma 2.1LetHbe a finite generated free abelian group of rankN.If theNelementsg1,···,gNgenerateH,then they form a basis ofH.

3 Necessary Tools

In this section,we construct some tools which are needed to prove the main results of this paper.They include some basic properties of Δn(Qm)and Qn(Qm).Recall that the generalized quaternion group of order 4m is defined as

Hence,each representation ρ of Qmdepends only on its values at g and h.Therefore,we use

to denote ρ.

The following theorem found in[1]classifies the similarity classes of all irreducible representations of Qm

Theorem 3.1Let

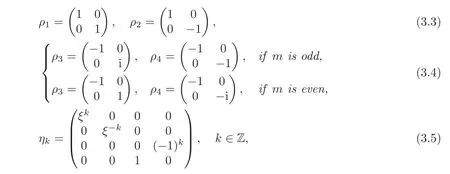
whereξ=.Then all distinct similarity classes of irreducible representations ofQmare

For later use,we remind the readers that by Corollary 2.1 and Theorem 3.1,Δn(Qm)has free rank m+2 for each natural number n.

In the rest of this section,we construct a basis of Δ(Qm)and show some of its basic properties.For convenience,we fix the following notation.Throughout,n and N are natural numbers.

(1)

(2)

(3)For any subset S⊂R(Qm),denote by ZS the set of all Z-linear combinations of elements of S.

(4)Denote by Cdthe cyclic group of order d.

It is easy to see that E,F,Yk∈Δ(Qm).Hence Sn,j(N)⊂Δn(Qm).

Lemma 3.1Δ(Qm)is the free abelian group based on

ProofNote that the cardinality of Bmis m+2.So by Lemma 2.1,we only need to show that it generates Δ(Qm).Let

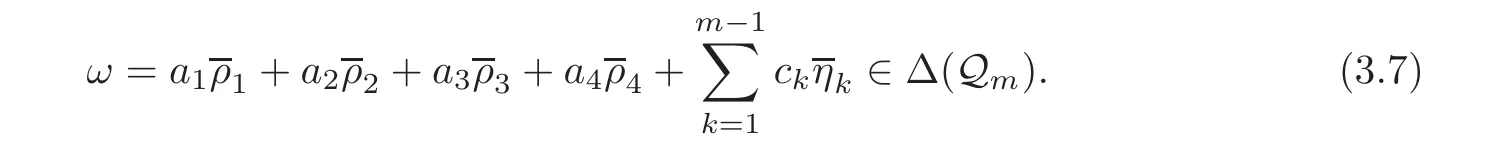
Then a1+a2+a3+a4+=0.Short calculations show that

So

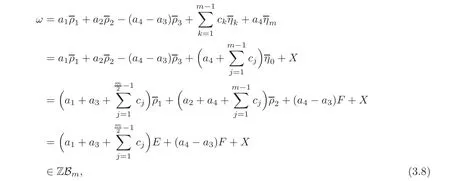
where

Proposition 3.1Regarding elements ofR(Qm),we have the following assertions:

(1)Ykdepends only on the residue class ofkmodulo2m,andYk= −Y2m+1−k.Thus theset{Yk|k ∈ Z}is equal to{Y1,···,Ym}.

(2)E2=2E,EF=

(3)

(4)

(5)ZSn,j(N)=Z{Fj(Yk−(2k−1)Y1)|2?k?N+1},when0?j?n−2.

ProofOne can easily verify(1)–(3)by calculating the characters of relative representations.

For(4),a short calculation shows that χηkχηl= χηk+l+ χηk−l.So

Hence

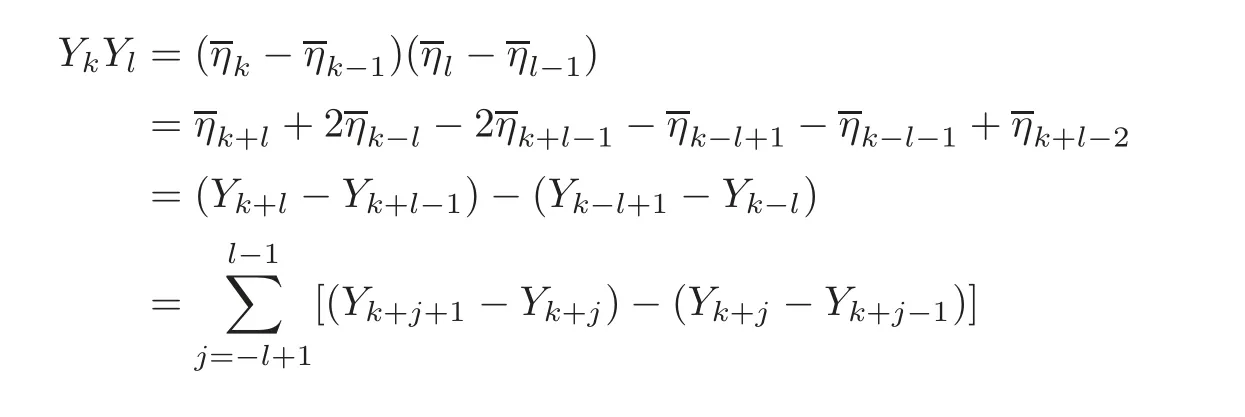
We now consider(5).Due to(4),we get

Recall that Y0=−Y1.So for each natural number N,

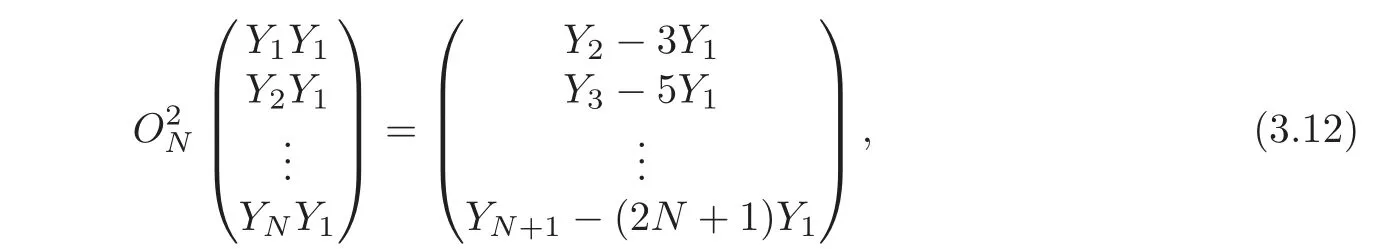
where

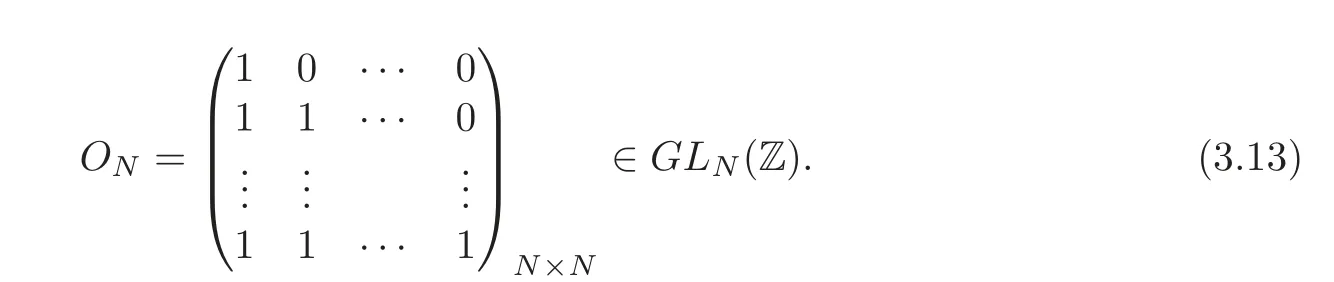
Therefore

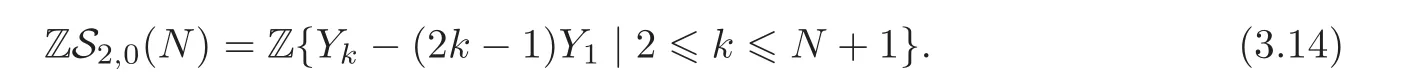
From this,(5)follows.

4 Structure of Qn(Qm)

This section is divided into two subsections,according to when m is even or odd.

4.1 m is an even number

We first give a basis of Δn(Qm)as a free abelian group.The following lemma is simple but useful.

Lemma 4.1For any1?j?n−2,Sn,j+1(m)⊂ZSn,j(m).

ProofIt is easy to see that we only need to show S3,2(m)⊂ZS3,1(m).By Proposition 3.1,we get

Note that,so

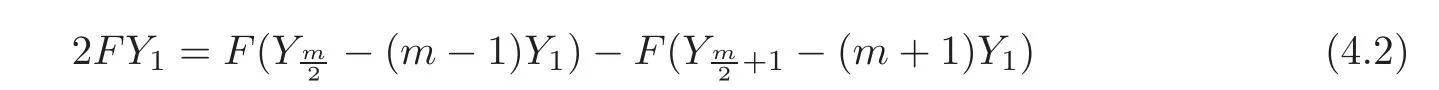
lies in ZS3,1(m).So does 2FYk(2?k?m),since it equals

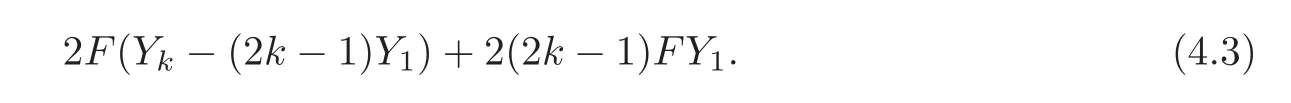
From this,the lemma follows since F2=2F.

Theorem 4.1For anyn?2,Δn(Qm)is the free abelian group based on

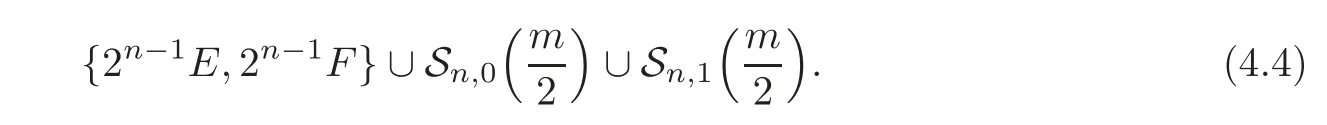
ProofNote that(4.4)has cardinality m+2.So by Lemma 2.1,we only need to show that it generates Δn(Qm).Due to Lemma 3.1 and the fact that EYk=0,we get,for any n2,Δn(Qm)is generated by

and all products

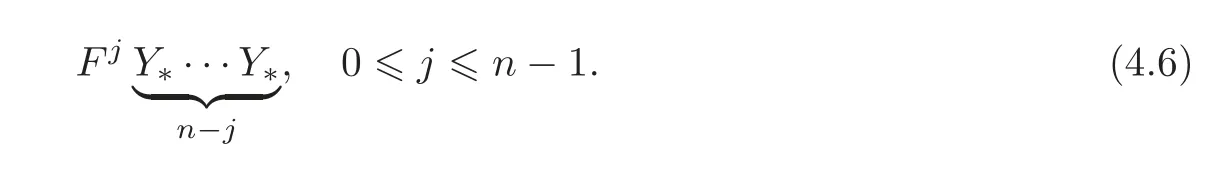
A short calculation shows that(4.5)equals{2n−1E,2n−1F,2n−2EF}.In addition,the generator 2n−2EF can be omitted since

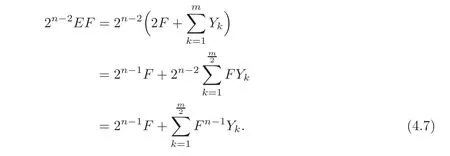
By Proposition 3.1,YkYl∈ ZS2,0(m).Hence,Δn(Qm)is generated by

Moreover,Lemma 4.1 implies that Δn(Qm)is generated by

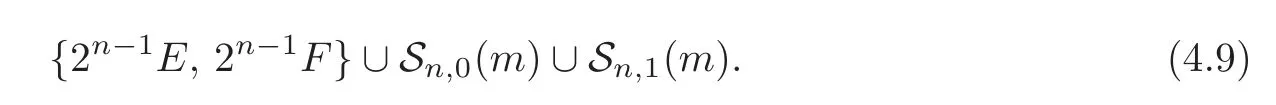
Recall that

So

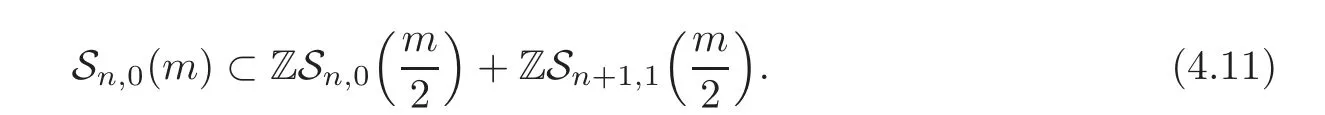
In addition,one can easily verify that

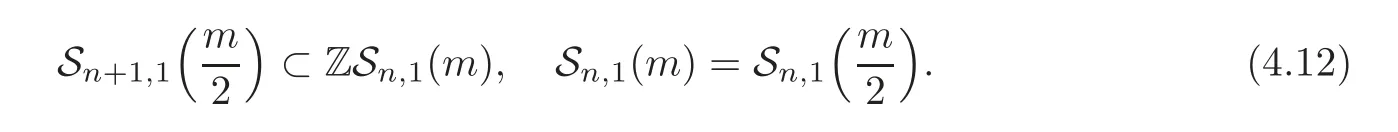
It follows that Δn(Qm)is generated by(4.4).

Now we come to the main result of this subsection.

Theorem 4.2Whenmis an even number,we have

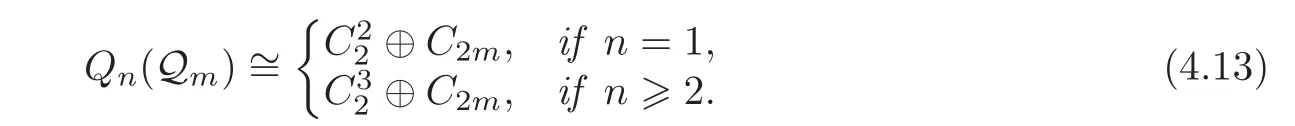
ProofBy Proposition 3.1 and Theorem 4.1,we get

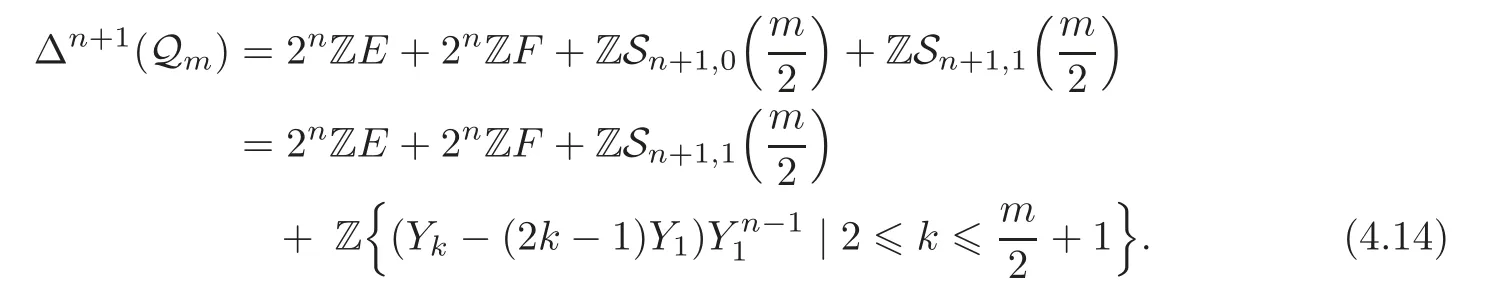
Note that

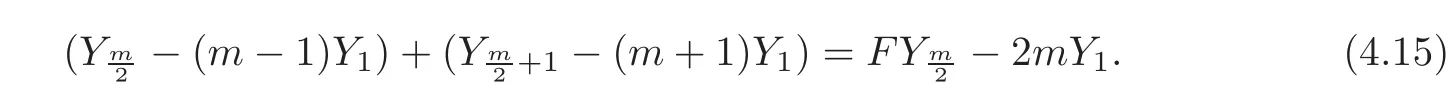
So

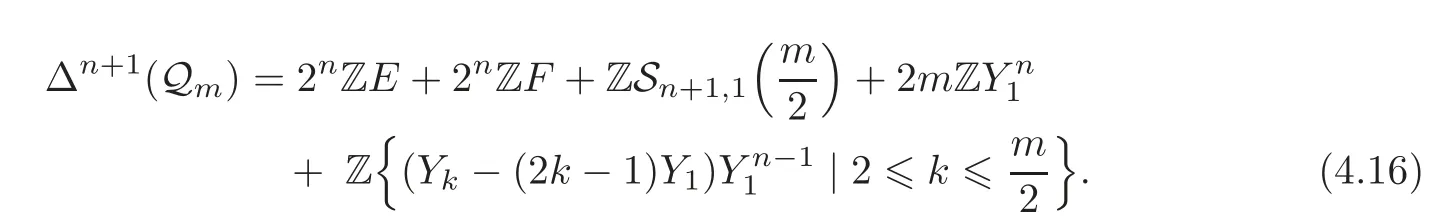
We consider the case Q1(Qm) first.It is easy to see that Δ(Qm)has the basis

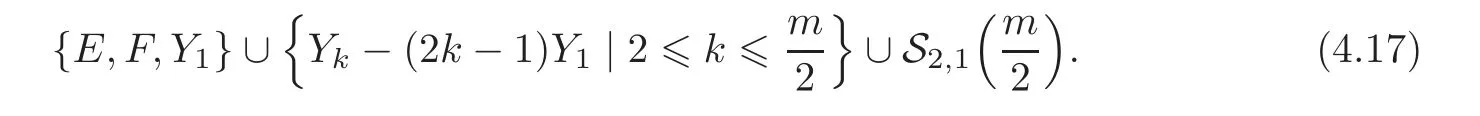
Thus

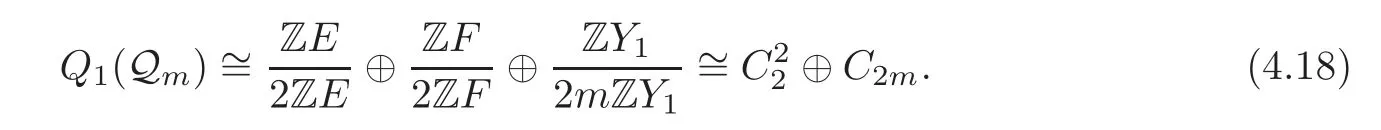
Secondly,by Proposition 3.1,for any n?2,

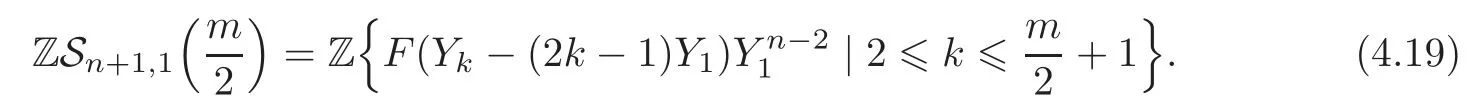
Applying(4.2),we get that(4.19)equals

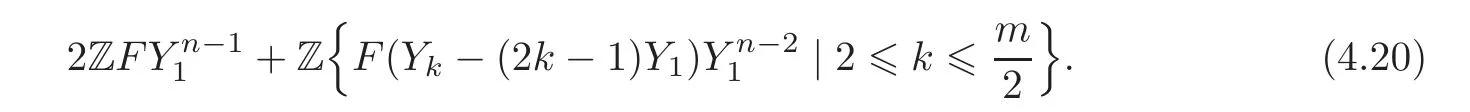
Therefore

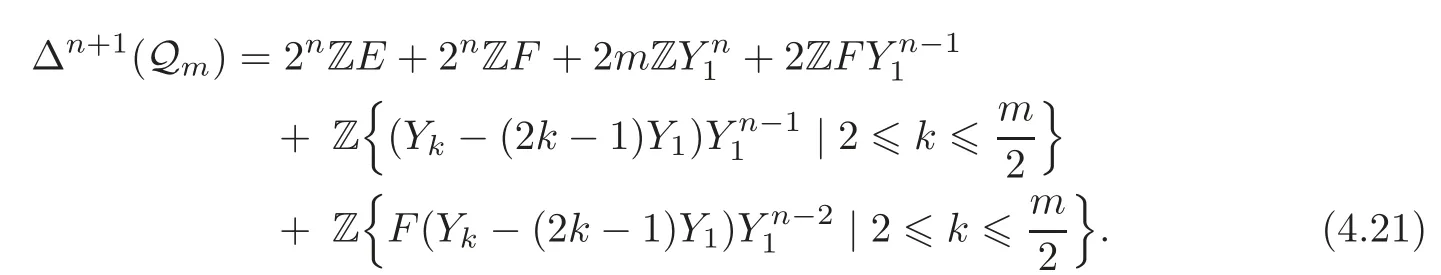
Like in(4.17),Δn(Qm)has the basis

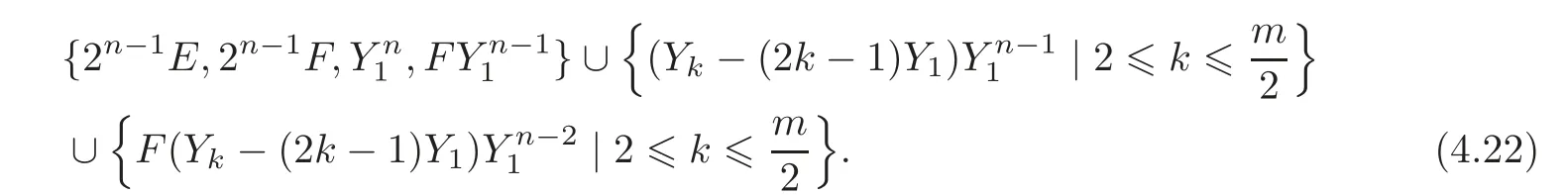
Thus

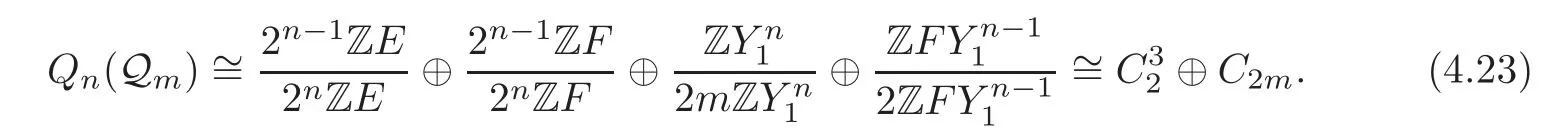
(4.18)and(4.23)together finish the proof.

4.2 m is an odd number

We study this case by using the same method as in the above subsection.

Lemma 4.2For anyn?2,

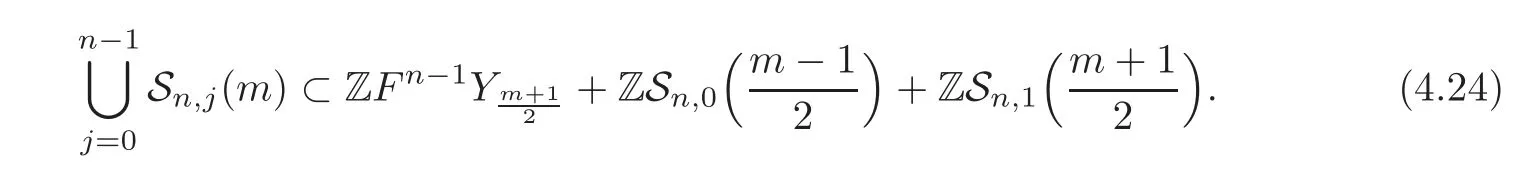
ProofRecall thatSo

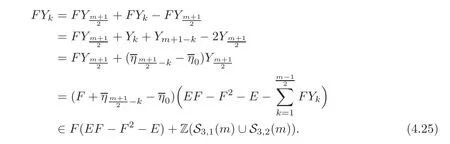
Short calculations show that

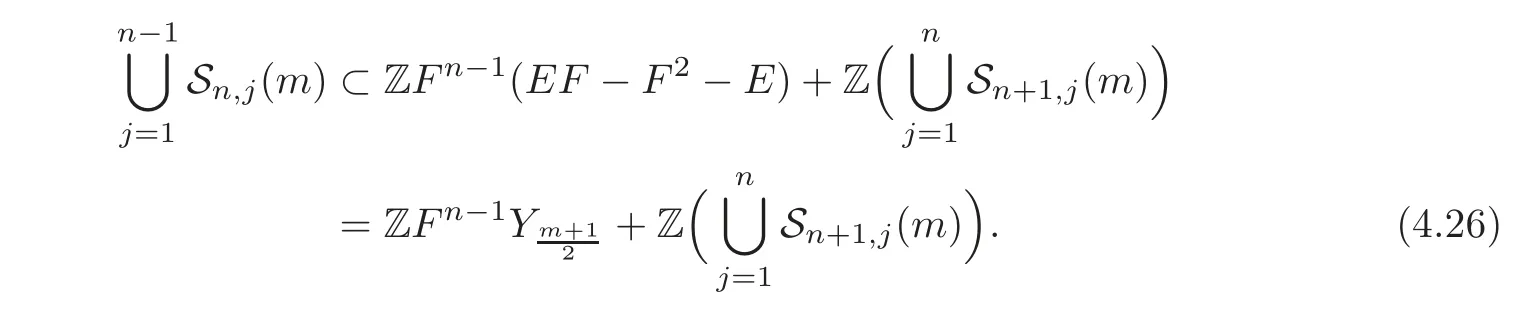
Hence,by the fact thatwe get

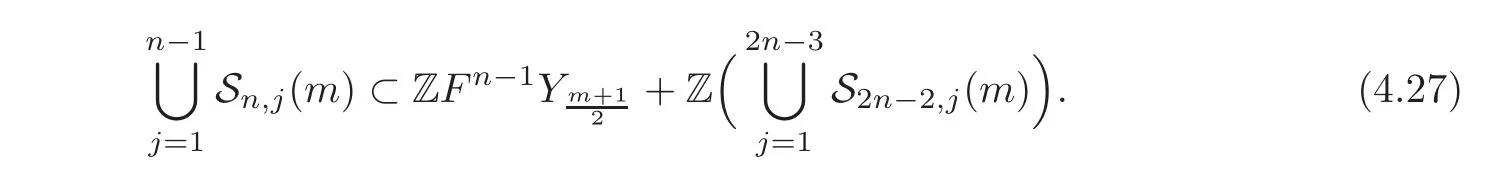
Note that F2Yk=(2F−E)Yk=2FYk.From this,it follows that

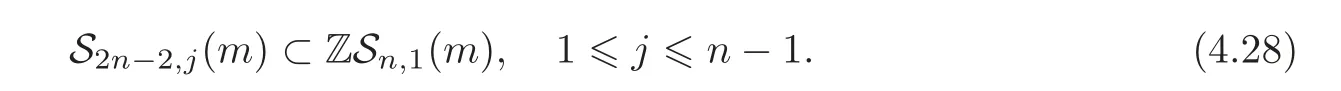
Forwe have

since 2Sn,∗+1(m) ⊂ Sn,∗(m)in this case(as Lemma 4.1).So

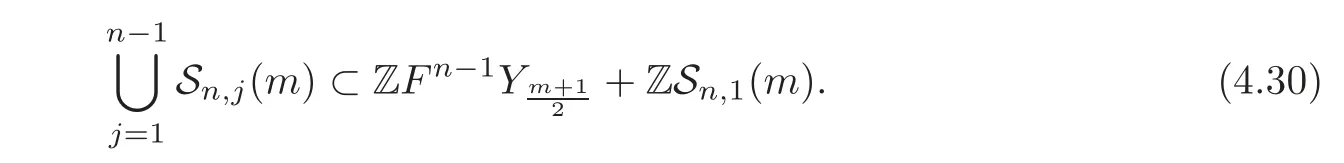
Now consider Sn,0(m).Sinceand

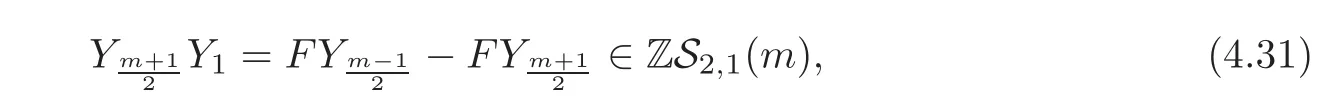
we have

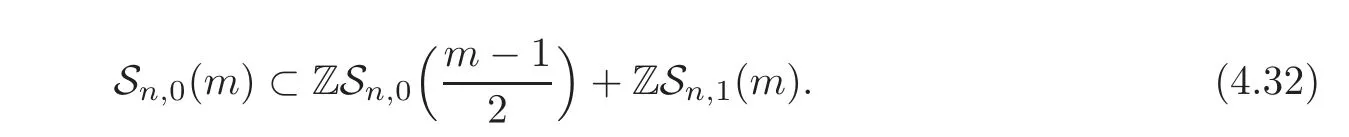
Then the lemma follows from the fact that

Lemma 4.3For anyn?2,

ProofThe lemma is trivial for n=2.Assume n?3 in the sequel.Then for any 2?j?n−1,we have

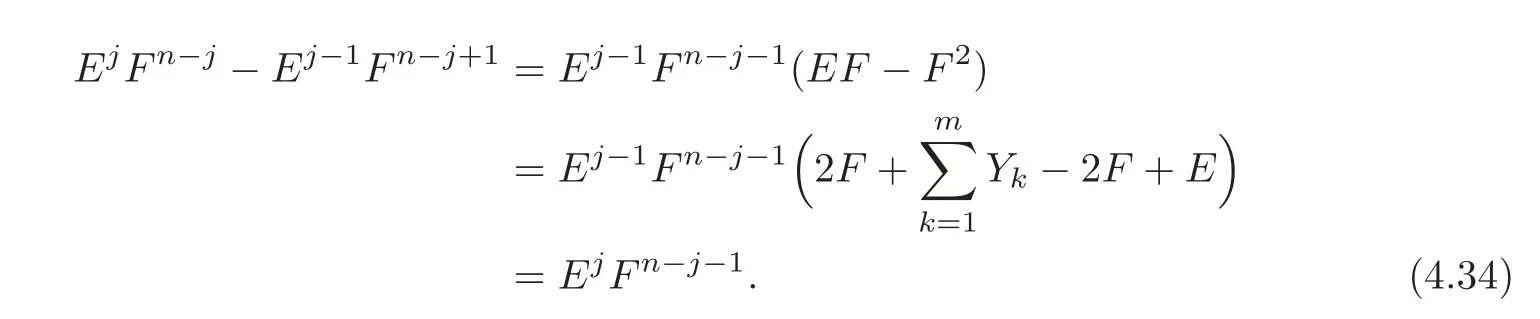
Hence the lemma follows from Ej+1Fn−j−1=2EjFn−j−1since E2=2E.

Lemma 4.4For anyn?2,Δn(Qm)is generated by

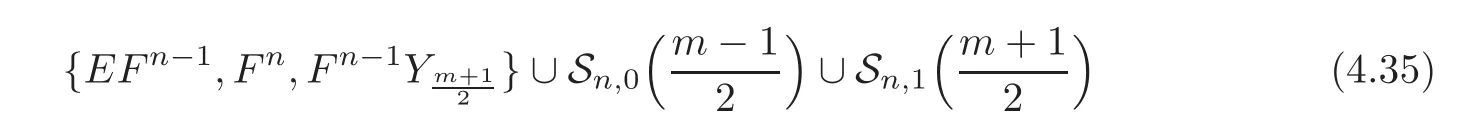
as an abelian group.

ProofDue to Lemmas 4.2–4.3,Δn(Qm)is generated by

So we only need to show that(4.35)generates E2Fn−2.Short calculations show

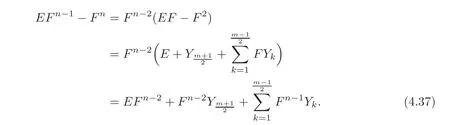
Hence,by the identities E2=2E andwe get

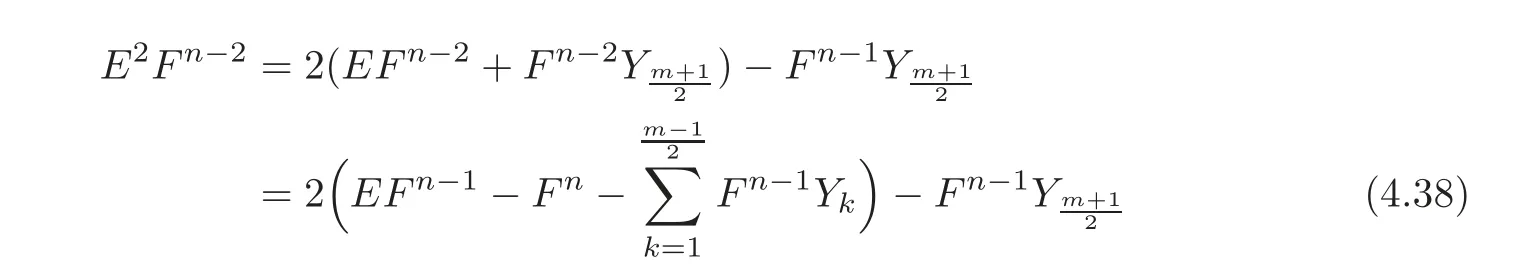
as required.

Corollary 4.1For anyn?3,Δn+1(Qm)is generated by

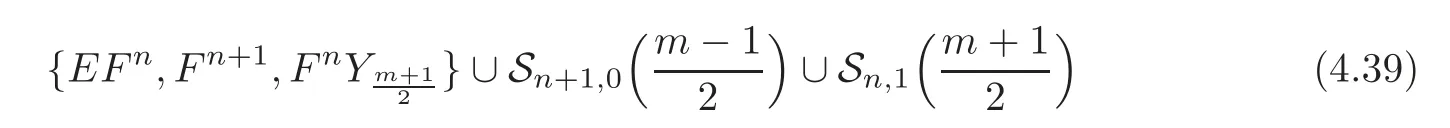
as an abelian group.

ProofIt is easy to see that

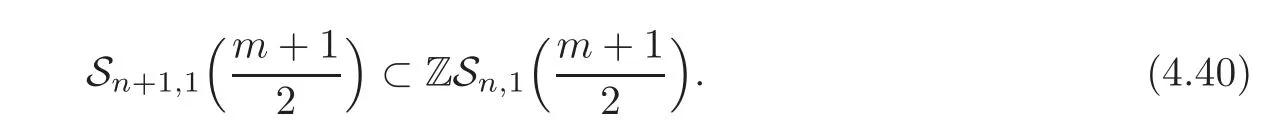
So by Lemma 4.4,we just need to show

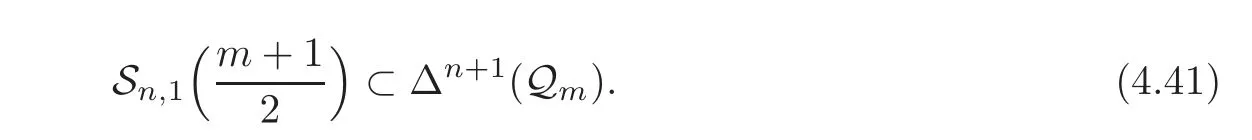
Due to(4.25),we get

Hence

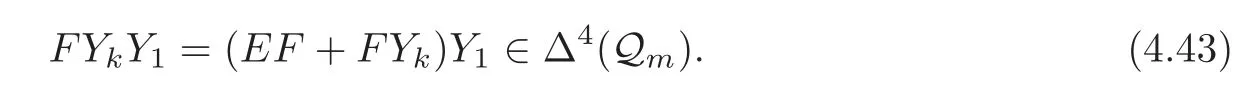
From this,the corollary follows.

Theorem 4.3For anyn?2,there exist three integersan,bn,dnwith2n−2bn+andn=1such thatΔn(Qm)is the free abelian group based on

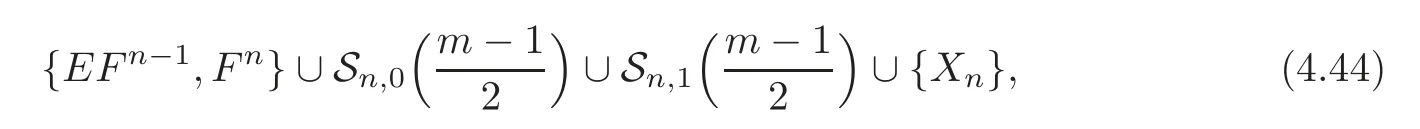
where

ProofNote that(4.44)has cardinality m+2.So we just need to show that(4.44)generates Δn(Qm).Moreover,we only need to show that it generatesa ndby comparing it with(4.35).The theorem is trivial for n=2 by setting b2=0,a2=d2=1.

Assume n?3.By(3.12)and a short calculation,we get

where

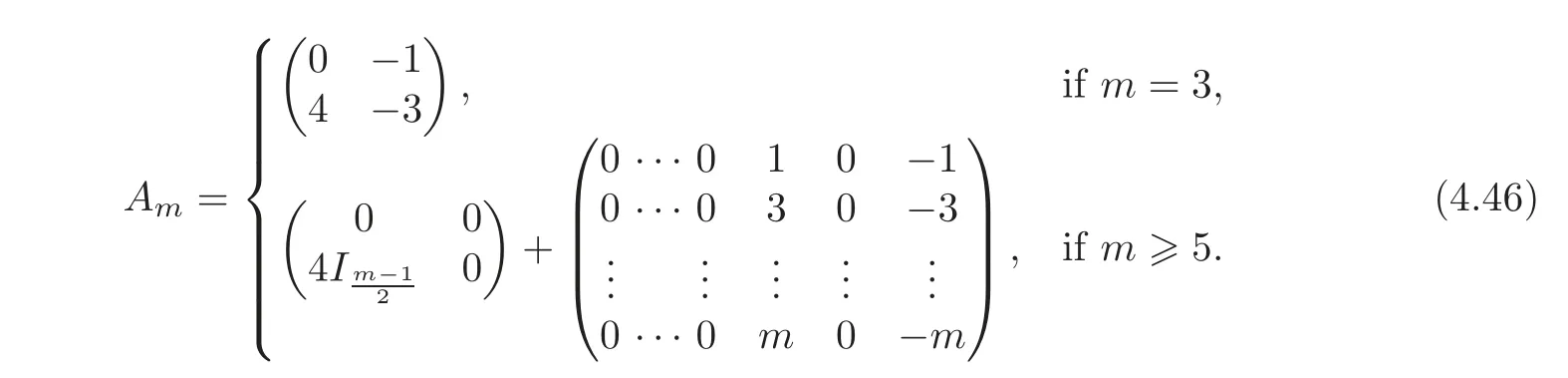
From this,it follows that

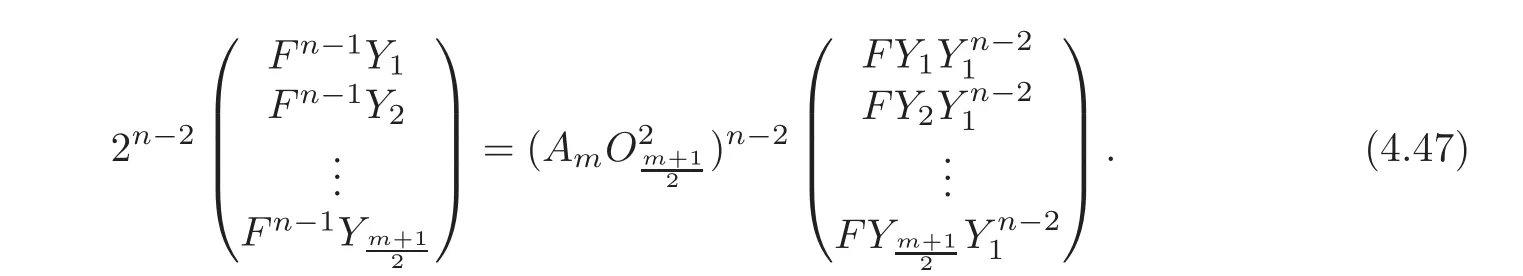
Consider the matrixBy direct calculation,we get

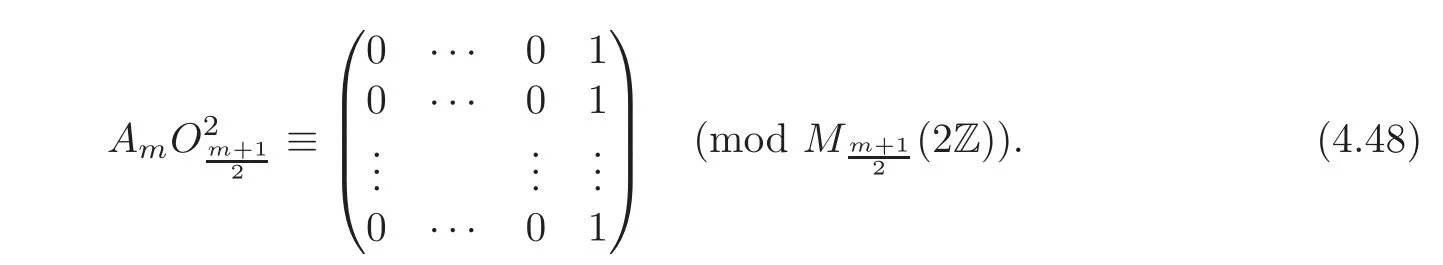
Hence

Denote by dnthe integer in the lower right-hand corner ofSet

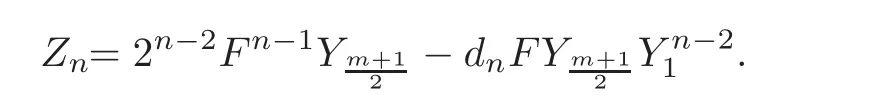
Then

(1)dnis odd,so there exist two integers an,bnsuch that 2n−2bn+andn=1,

(2)

Therefore,either

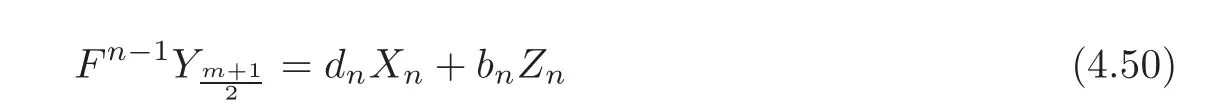
or

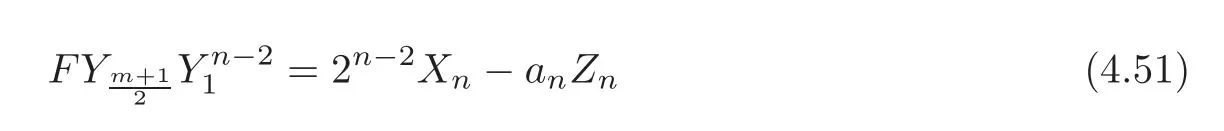
is generated by(4.44),as required.

Theorem 4.4Whenmis an odd number,we have,for any natural numbern,

ProofWe compute Q1(Qm) first.By Lemma 4.4,

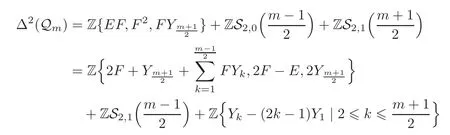
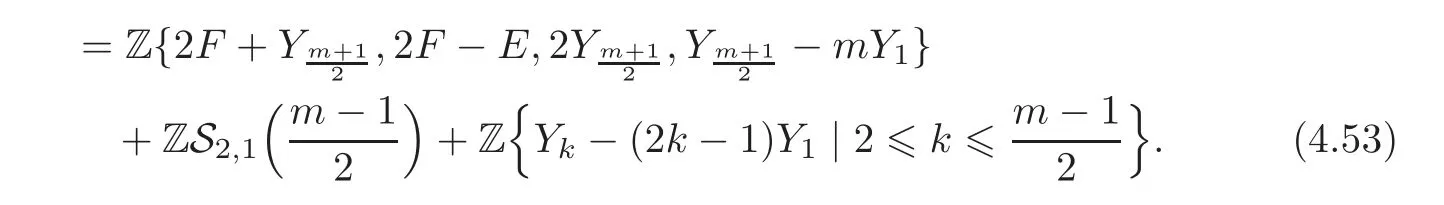
The first part of the right-hand side of(4.53)equals

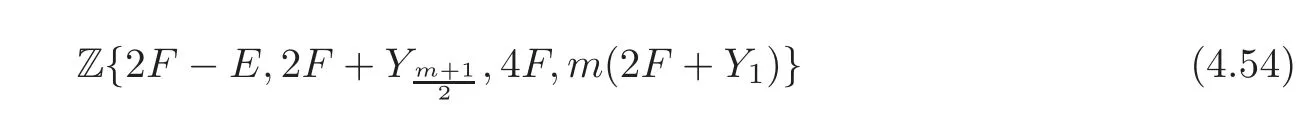
since

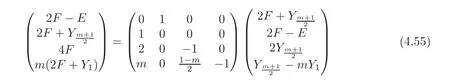
and the square matrix lies in GL4(Z).It is easy to verify that Δ(Qm)has the basis

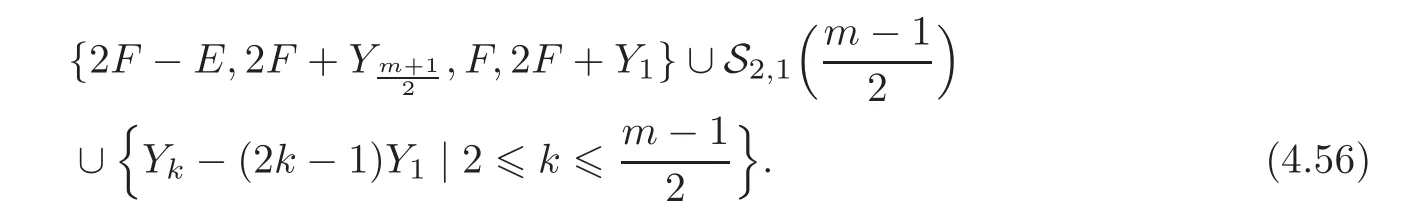
So

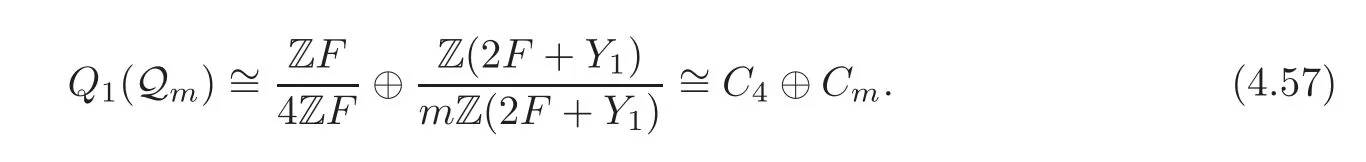
Secondly,by(4.31),we get

The first part of the right-hand side of(4.58)equals

since

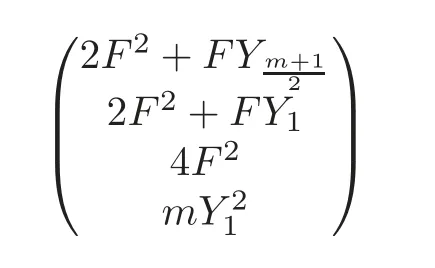
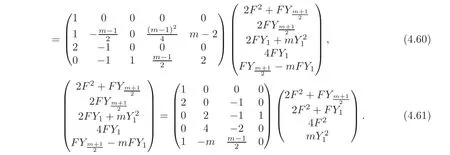
Due to Theorem 4.3,one can easily verify that Δ2(Qm)has the basis

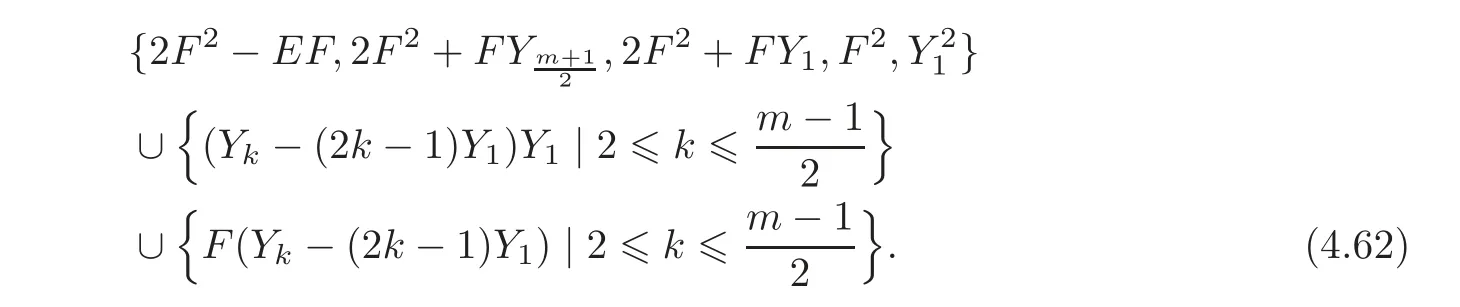
Thus

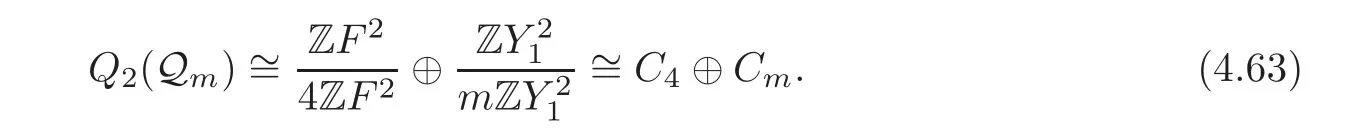
Finally,by Corollary 4.1 and(4.31),we get,for any n?3,

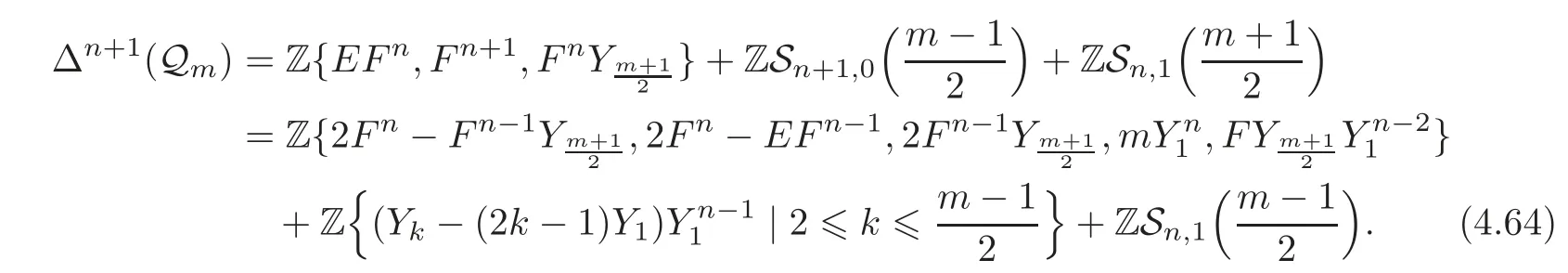
Thanks to(4.50)–(4.51)and the fact thatlies inthe first part of the right-hand side of(4.64)can be replaced by

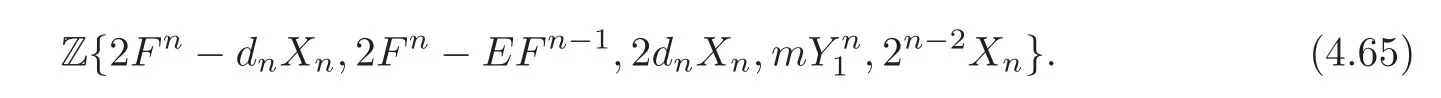
Recall that dnis an odd number,which implies gcd(2dn,2n−2)=2.From this,it follows that(4.65)equals

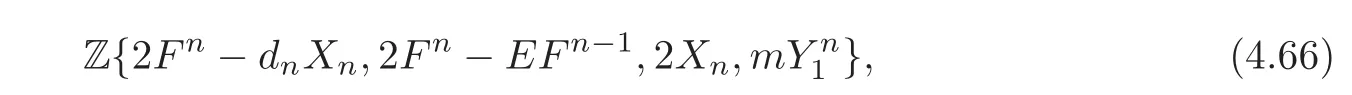
and hence it equals

since

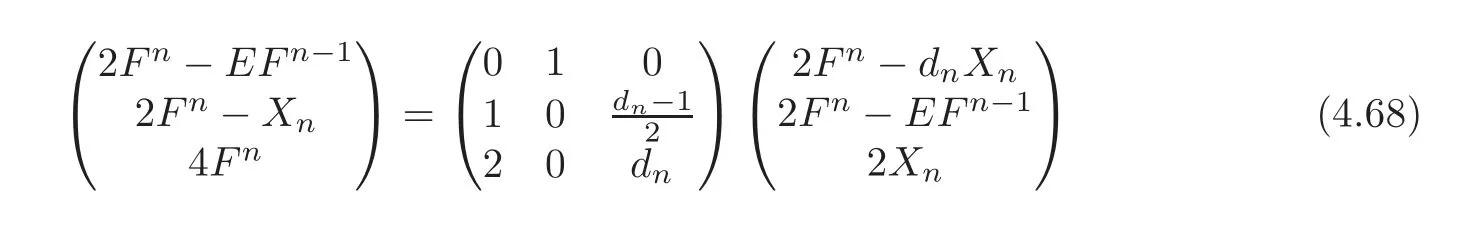
and the square matrix lies in GL3(Z).Due to Theorem 4.3,Δn(Qm)has the basis

Therefore,for any n?3,

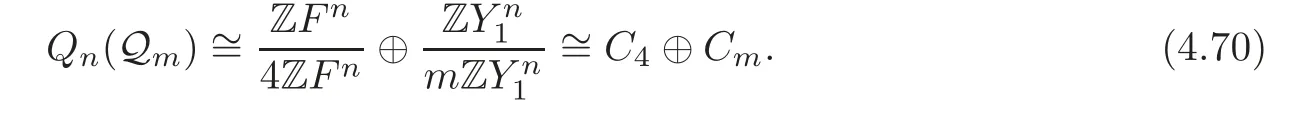
(4.57),(4.63)and(4.70)together finish the proof.

AcknowledgementThe author wants to express his sincere gratitude to Prof.Tang Guoping for his encouragement and support.

[1] Fulton,W.and Harris,J.,Representation Theory:A First Course,Springer-Verlag,New York,1991.

[2] Curtis,C.W.and Reiner,I.,Representation Theory of Finite Groups and Associative Algebras,American Mathematical Society,Providence,2006.

[3] Chang,S.,Chen,H.and Tang,G.P.,Augmentation quotients for complex representation rings of dihedral groups,Front.Math.China,7,2012,1–18.

[4] Chang,S.,Augmentation quotients for complex representation rings of point groups,J.Anhui University(Natural Science Edition),38,2014,13–19.

[5] Chang,S.,Augmentation quotients for real representation rings of cyclic groups,Front.Math.China,preprint.

[6] Karpilovsky,G.,Commutative Group Algebras,Marcel Dekker,New York,1983.

[7] Chang,S.and Tang,G.P.,A basis for augmentation quotients of finite abelian groups,J.Algebra,327,2011,466–488.