基于行列式计算的几种特殊计算方法解析
2019-05-17王俊花
王俊花
(大同大学 浑源师范分校, 山西 浑源 037400)
1 行列式计算方法简介及基本说明
行列式多用于线性方程组的求解,是一种速记的表达式,现在已成为线性代数中一种十分有用的工具。行列式计算有一定法则,对于线性方程组而言,应用行列式计算,它可以将线性方程组的不同解表示成一个公式,即行列式也可以表示为一个数,因此行列式是解线性方程组的重要工具[1]。随着线性代数研究的深入完善,行列式计算已逐渐独立在线性方程组之外,并发展成为一门独立学科理论,其中最经典的著作是英国著名数学家卡罗尔的《行列式———计算数值的简易方法》,因此,行列式不仅仅是一种计算方法,更是一种知识理论体系,因此,对于行列式计算方法研究很有必要。
行列式的计算方法类型多样,有较强的技巧。当然,任何一个n阶行列式都可以根据行列式的定义去计算数值,但是,由定义可知,n阶行列式展开后有n!项,计算量大,通常情况下不用该方法,除非行列式中有多个零元素。对于行列式的计算方法,通常用到的是化三角形法与按行、列展开法,其主要依据行列式性质应用。由于行列式计算化三角法特殊性的特点,行列式计算必然没有那么简单,不易掌握。为了有效解决实际问题中行列式计算相关方面问题,使其在工程领域计算中变得简单,本文运用相关理论知识[2]给出几种计算行列式的方法,并希望可以其有效推广,使教学环节变得容易,开拓学生视野,使课堂教学应用更为简便。
2 行列式几种特殊计算方法解析
2.1 运用变向化三角形法计算行列式
化三角形法是将行列式化为下(或上)三角形行列式或对角形行列式计算的一种方法,同时,这也是行列式计算基本方法。一般情况下,每个行列式都可以运用行列式性质化成三角形行列式计算。但是,对于某些阶数较高的行列式,计算十分繁琐,所以,有些情况下,先是根据行列式性质将其变形,然后再对其化简成三角行列式,减少计算量。例如:
例1 计算行列式

解析:很显然,如果将该行列式直接去化三角形行列式,计算繁琐,无规律可言,这里本文重点运用行列式性质。注意到,该行列式从第一列开始,每一列与该列中n-1个数字相差1,根据行列式性质,首先从n-1列开始每个数均乘以-1加到第n列,第n-2列乘以-1加到第n-1列,以此类推,直到第1列乘以-1加到第2列[3]。其次,将第一行乘以-1加到每行上去,这样再将行列式化为三角形行列式,计算简化。


其中:ci—行列式第i列;
ri—行列式第i行。
问题推广:该例中,明显1,2,…,n-1,n,这n个数字在循环,如果n个无规律的数字在循环,这样的行列式又该如何计算呢?将这样的行列式称为“循环行列式”,因此,这样的行列式可以推广到一般情形[4]。例如:
的值


在这里un=1,用到u=un+1,其中f(u)=a0u+a1u2+…+an-1un。
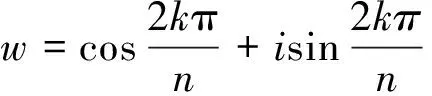
因此,1,w,w2,…,wn-1互异且都是单位根,记:

由上述可知:Awj=f(wj)·wj,所以
Aw=(Aw0,Aw1,…,Awn-1)
=(f(w0)·w0,f(w1)·w1,…,f(wn-1)·wn-1)
显然w=

因为|w|≠0,因此|Aw|=|w|·f(1)·f(w)·…·f(wn-1)=|A||w|,所以,
|A|=f(1)·f(w)·…·f(wn-1)


从而有:

由此可见,该结论与例1答案吻合,该问题可以推广到一般情形。
2.2 运用降阶法计算行列式
一般情形下,行列式按行(或列)展开并不能减小计算量,只有当该行列式中某一列(或某一行)元素零多时,才可以真正发挥作用。因此,行列式应用按行(或列)展开时,首先根据性质将某一列(或行)化为较多零元素,再开始展开[5]。例如:
例3 计算行列式

解析:该式中没有一个零元素,如果直接展开逐步降阶直到化为2阶行列式计算,需要20!×20-1次乘法加法运算,根本无法完成。若果运用行列式性质将其化成有多个零元素,则可以很快计算出结果。值得注意的是,该式中相邻两行(或列)对应元素仅相差1,可按如下方法进行计算。
解:


2.3 运用加边法计算行列式
有些行列式,为计算简便需要在原基础上加上一列一行,这种方法称为加边法。需注意,加边后行列式值不变,得到高阶行列式计算容易,根据行列式特点选取所加行和列,首要是观察每一行或每列是否有相同的因子[6-7]。例如:
例4 计算行列式

解析:该行列式若主对角线元素都减去1,可以明显看出第一行元素x1与x1,x2,…,xn相乘,第二行为x2与x1,x2,…,xn相乘,……,第n行为xn与x1,x2,…,xn相乘,这样就可以知道行列式中每行都含有相同因子x1,x2,…,xn,所以可以运用加边法进行计算。

说明:加边法最大的特点是需要找出行列式中每行(或列)中相同的因子,这样,在升阶后即可根据行列式性质把大部分元素化为零,再化三角形行列式,达到简化计算的目的。
2.4 运用乘法定理计算行列式
对行列式计算时,某些情况可以应用乘法定理,即可以将行列式表示成两个便于计算或者已有结论的行列式的乘积,这样可以较快计算出所给行列式的值。也有些情况,可以不用直接计算,恰当选取一个与已知行列式同阶数的行列式,并计算两行列式乘积,这样也可以计算出所给行列式值,使计算简化。例如:
例5 计算行列式

解:由题目可知:该行列式可以表示为如下两行列式乘积,记为A。

由此可见:当n>2时,A=0;当n=2时,A2=(a2-a1)(b2-b1);
当n=1时,A1=1+a1b1。
3 结 论
行列式计算是线性代数中一个重要知识点,也是一个难点,且行列式计算在实际问题解决中应用广泛,因此,目前对于行列式计算方法研究,越来越受到关注,是一个值得研究的课题。对于行列计算,还有许多特殊且很实用的计算方法,如极限法、导数法、差分法、换元法、积分法等,但这些方法用处不多,所以不加以介绍。对于常见的最基本方法,如定义法等,本文也未涉及,本文结合所学知识主要从四个不同角度分别给出四种不同的计算方法,有一定局限性,对于相同类实际问题可以有效解决,但对于某些问题,可能起不到好的作用,希望在后续研究中继续挖掘,继续探讨。
