非线性Julia集的复迭代生成原理及丝绸印花图案设计

朱海祥(苏州市职业大学 教育与人文学院，江苏 苏州 215104)



非线性Julia集的复迭代生成原理及丝绸印花图案设计

朱海祥
(苏州市职业大学 教育与人文学院，江苏 苏州 215104)

摘 要：Julia集是研究复平面中初始点集的轨迹动力学性态，具有分形自相似特性.通过对Julia集生成原理的研究，清晰且快速地掌握其生成流程中的数学背景.进一步改变其阶数、常数、缩放值、颜色参数及配色算法，可产生许多变化多样、造型奇特的应用型图形.并探讨应用Julia集图形进行丝绸印花图案设计的途径.

关键词：Julia集；分形图形；原理；图形设计

Julia集是研究复平面中初始点集的轨迹动力学性态，是复动力系统中重要的分形，具有分形自相似的特性.与一般的分形图形相比，结构更加复杂，内涵更加丰富，受到许多数学应用学者的关注.同时随着分形软件的开发和应用，生成许多基于Julia集的可视化艺术图形.分形图形的强烈视觉效果已受到人们的极大关注，如果能够掌控并为设计师所用，再结合艺术家的思维，将真正实现科学与艺术的完美结合[1].为了开发出更具特色和效用的分形图形，需要对迭代函数类型、图形映射变换、配色算法的公式及参数进行新的设置或创建，这就要求具备分形生成的数学基础，熟悉相关参数的数学意义，而大部分使用分形软件的人员并不具备Julia集的数学背景，已有研究也较少揭示相关参数和生成分形的内在关系.本文拟结合Ultra Fractal分形软件生成的Julia集，研究Julia集生成的相关数学和计算机原理，以期掌握并设计出更具适用性的分形图形.

1 非线性Julia集的复迭代生成原理

1.1 相关函数

现以函数f(z)=z2+c(z∈C，c为复常数)为例探究初始点的迭代走向，z0为复平面上任意一点，根据函数f(z)，得到迭代公式zn+1=f(zn)=zn2+c，产生迭代序列：z1，z2，z3，…，zn，则每个初始点z0迭代后在复平面上产生一条轨迹，轨迹的走向有收敛和发散两种情况，即轨迹有界或者无界.

在复平面上有一些特殊点，对研究Julia集的形状和性态有着重要的作用.比如临界点，对于任意函数f(z)，若f'(z0)=0，则称z0为函数f(z)的临界点.k周期点，对于函数f(z)，z0为复平面上任意一点，若有fk(z0)=z0，则称z0为函数f(z)的k周期点.若k=1，有f(z0)=z0，则称z0为函数f(z)的不动点.周期点又可分为吸引的和斥性的，若在z0的充分小δ邻域有fk(δ+z0)→z0，则z0为吸引的，否则为斥性的.

1.2 平面上的变换

对于任意z1、z2、k∈C，有f(z1+z2)=f(z1)+f(z2)，f(kz1)=kf(z1)，则f(z)为线性变换，否则为非线性变换.线性变换时，往往是逐渐进行的；而非线性变换时，往往有性质和图形上的转化和跳跃.这两种变换在分形图形生成上都有广泛的应用，分形图形的IFS生成法就是利用仿射变换(一种特殊的线性变换)生成，本文研究的Julia集都是非线性变换，相邻区域的点迭代走向和速度也不尽相同，当然生成的图形也更具艺术效果.

1.3 Julia集边界点的生成

复杂Julia集只要通过一个简单的复函数公式经过多次迭代就可以获得.Julia集主要研究起始点(复平面上的点)迭代后轨迹的走向，根据是否有界分为两个互不相交的子集.对于复杂的迭代函数，可以用周期点分类构造Julia 集，进行逐点迭代，可以达到任意精度，得到迭代的动力学过程和性质[2].对于一般的迭代函数，Julia集可以利用反函数迭代法生成[3].

研究发现，对于函数f(z)有无数个周期点，这些周期点可能为吸引的，也可能为斥性的，Julia集的吸引周期轨道至少吸引着一个临界点，而函数f(z)为二次多项式，有唯一临界不动点，最多只能有一个吸引周期轨道.因此对于函数f(z)，周期点绝大部分为斥性的，可取z0为其中一个斥性周期点，则z0的前像和后像都为斥性周期点.现考虑z0的前像，由于函数f(z)为二次多项式，则z0的逆像有两个点，这两个点的逆像又有四个点，如此重复下去，逆像的个数为2n的二叉树结构，则可构成Julia集，即Julia集为函数f(z)斥性周期点的闭包[3].此方法可以与迭代函数系统(IFS)结合研究，求斥性周期点前像的过程就可以看成两个非线性变换.

1.4 填充Julia集内部点的生成

前面生成的分形图形是Julia集，一般分形软件生成的是应用更为广泛的填充Julia集，对函数f(z)=z2+c反复进行迭代运算， 最后得到的值有三种可能性：z值趋向无穷大；z值趋向于零；z值是变化的非定值.趋向无穷和趋向于零的点叫定常吸引子，很多点被定常吸引子所吸引而结束[4].那些不趋向无穷和趋向于零的初始点的集合就组成了填充Julia集，记为Kc；Julia集是Kc的边界，记为Jc，这样可以确定初始点的归属情况.

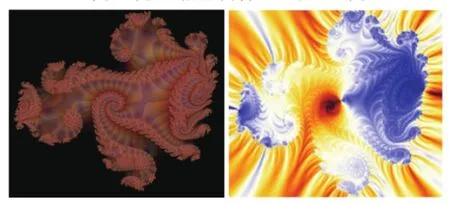
图1 同一函数不同迭代次数生成的Julia图形

首先考虑的是如何判断初始点经过迭代后的轨迹是否有界，通过分析z1，z2，z3…，zn，前面几个点可以发现该序列的趋势，这样一直计算也可以判断，但费时费力，也不利于计算机实现.对于二次复函数f(z)，可以证明，如果某个点zj到原点的距离满足|zj|≥2，则该序列将逃逸到无穷远，即为逃逸规则[3].根据逃逸规则可以判断初始点迭代轨迹的逃逸情况，有些初始点只需经过几次迭代就能确定其轨迹趋于无穷远；有些点却需很多次甚至无穷次才能逃逸到无穷远处，即可能出现某初始点迭代500次后到原点距离还是小于R，而第501次后到原点距离大于等于R.图1(a)迭代1 000次，图1(b)迭代100次，可以看出迭代次数选择越高，生成的Julia集越精确.但若每个点迭代次数选择过高，生成图形的耗时将会过长.迭代次数选择过低时很多轨迹发散的初始点被看成轨迹收敛点，影响生成图形的绚丽复杂程度.所以一般假定某个值N(可以为100、500等)为初始点迭代的次数，若所有迭代序列点到原点的距离小于R，则认为该初始点迭代轨迹有界，即该点包含于Kc；若存在一个迭代序列点到原点的距离大于等于R，则可认为该初始点迭代轨迹趋于无穷远.即该点不包含于Kc，由此可以生成填充Julia集的内部点.

2 丝绸印花图案设计

2.1 填充Julia集的配色方案

填充Julia集的配色方案可以由逃逸时间算法实现.对于每一个不同的多项式函数，不同的c值，都可以生成不同的分形图形.关键是如何描绘不同类型的初始点，由前面研究可以发现配色步骤，若初始点迭代次数nR，则该点迭代轨迹逃逸到无穷远，可以根据逃逸速度选择不同的颜色进行描绘；若初始点迭代次数n

结合上面配色步骤，可以选择不同配色方案.根据初始点迭代轨迹走向的异同，可以将轨迹未逃逸到无穷远的初始点绘成黑色，而轨迹逃逸到无穷远的初始点绘成白色，这样就可以得到2色的Julia集，但这样得到的图形略显单调，不能清楚显示Julia集精细的内部结构；考虑到初始点逃逸到无穷远点的速度快慢，对初始点分类进行绘色，如逃逸迭代次数除以24后取余数，余数相同则着色相同，这样通过优化得到的Julia集具有很好的视觉效果.

另外，若想进一步提高所得图形的内涵和外观，可以利用分形软件的着色渐变功能、分形内部和外部着色算法，根据需要对颜色、变化区间和算法进行选择和设置.图2-图4是对同一函数实施不同着色效果后生成的图形.图2通过改变图形渐变控制点的颜色，生成不同颜色配置的Julia图形，一般都可以根据实际需要，选择任意可能的颜色进行Julia图形的创作.图3中两个图形都是通过增加渐变控制点数目，生成了更加绚丽精细的图形，实际创作时可以增加任意多个控制点，增加图形颜色的丰富程度，得到颜色连续变化的图形.图4中两个图形利用不同的配色算法，在色彩控制方面有着独特的优势，生成各具特色的Julia图形.

图2 同一函数不同着色下的Julia图形

图3 同一函数不同数目渐变控制点下的Julia图形

图4 同一函数不同配色算法下的Julia图形

2.2 不同c值和缩放值的Julia集图形设计

对于每一个不同的c值，函数fc都可以生成不同的分形图形，如图5所示，这些分形图形从形状上可以分为两类：连通的和非连通的.

一个多项式的Julia集是连通的当且仅当它的所有临界轨道是有界的. 如果所有的临界轨道都趋向无穷远点， 那么这多项式的Julia集是完全不连通的[5].对于函数fc(z)=z2+c来说，有唯一的临界点0，若临界点的迭代轨迹有界，则Kc(f)为连通的；若临界点的迭代轨迹无界，则Kc(f)为非连通的.图5为c取不同值时Kc(f)的形状.图5(a)为连通的，图5(b)为非连通的.

分形都具有自相似性，如熟悉的Cantor集、方块分形、科赫雪花、谢尔宾瑟基三角垫等分形图形具有严格的自相似，每一部分都与整体相似；而Kc集是近似自相似的，每一部分放大后，与整体形状基本相似.在计算机上生成是以复平面上的一个域作为观察对象的.如果要实现放大，只要像素矩阵的规模不变，同时将集合观察范围缩小，这样便可实现集合的局部放大[6].图6显示的是依次对前图局部放大后生成的分形图形.当然一般近似自相似都有一定的尺度范围，超过这个范围就不具有近似自相似性.

图5 不同c值的Julia图形

图6 同一函数局部放大后生成的Julia图形

2.3 基于Julia集图形在印花图案设计中的应用

Julia集具有非线性、复杂性、精致性和数字化的特征，但多数为单独纹样，一般无法直接应用于纺织品图案设计中，为了实现其在丝绸上的应用，需要利用Photoshop和无缝拼接软件Xfader对选中的各种分形进行二次设计，生成二方或四方连续纹样，以满足不同的设计需求。随着印染设备技术的进步和普及，若要将纹样应用在丝巾或丝绸服装上，只需从成千上万个精美的纹样中选择一些符合丝绸细腻特征的图案，提送至电子提花机，再借助于电子喷印机即可实现印花设计，生产出具有高精度的丝绸图案。

3 结论

Julia集是以初始点为研究对象而生成的分形图形，若以参数c为研究对象，则可以生成另一种重要的分形图形M集，它指的是使Julia集为连通的参数c的集合，即M集的生成与函数的临界点有关，M集的图形性质及其与Julia集的关系值得进一步去研究.另外，前面讨论的函数f(z)都是复平面上的二次函数，若z的幂为任意实数时，或者是这些幂函数的代数和时，又该选择怎样的收敛半径和迭代次数，又会生成怎样的图形，隐藏什么样的规律，这些需要深入研究，进一步为分形艺术创作提供更多素材，并能够在丝绸印染、服装设计以及装潢设计等方面得到广泛的应用.

参考文献：

[1] 蔡燕燕，宋晓霞． 基于Julia 集分形图形在服装图案设计中的应用[J]． 上海工程技术大学学报，2011(2)：171-174．

[2] 邓学工． 复映射族f(z，c)=z-2+c 的Julia 集[J]． 东北师范大学学报:自然科学版，2003，35(5)：429-432．

[3] 朱华，姬翠翠． 分形理论及其应用[M]． 北京：科学出版社，2011．

[4] 徐淑平，李春明． 分形图的生成算法研究[J]． 微机发展，2005(9)：4-6．

[5] 吕菁，邱维元． 偶四次多项式Julia集的连通性[J]． 数学年刊，2003(4)：399-406．

[6] 楼越焕，沈德荣． 复数分形算法的计算机实现[J]． 上海电力学院学报，2010(5)：509-513．

(责任编辑：沈凤英)

引文格式： 朱海祥.非线性Julia集的复迭代生成原理及丝绸印花图案设计[J].苏州市职业大学学报，2016，27(2)：10-13.

中图分类号：O469

文献标志码：A

文章编号：1008-5475(2016)02-0010-04

DOI：10.16219/j.cnki.szxbzk.2016.02.003

收稿日期：2015-11-20；修回日期：2015-12-20

基金项目：江苏省丝绸织绣产品功能检测试验基地建设资助项目;苏州市职业大学青年基金资助项目(2014SZDQ02)

作者简介：朱海祥（1981-），男，江苏海安人，讲师，硕士，主要从事数学应用研究.

On Compound Iteration Generation Principle of the Nonlinear Julia Sets and the Pattern Design in Silk Printing

ZHU Hai-xiang
(School of Education and Humanities，Suzhou Vocational University，Suzhou 215104，China)

Abstract：Julia sets study the trajectory dynamics of the initial point set on the complex plane， which have fractal self-similar characteristics. The study of the principles of the Julia set generation enables clear and rapid mastery of its mathematic background in the process. The further alteration of the order number， constant， scaling value， color parameters and matching algorithm produces variably and peculiarly molded graphics. This paper mainly addresses the application of Julia set graphics to the pattern design in silk printing.

Key words：Julia set；fractal graphics；principle；the graphic design