Numerical Simulation of Free Surface for Navier-Stokes Equations∗

HUANG Yu-ping,LUO Zhi-qiang

(School of Science,Kunming University of Science and Technology,Kunming 650500)

Received:13 Mar 2015.Biography:Huang Yuping(Born in 1986),Female,Master.

Accepted:10 Nov 2015.Research fi eld:computational mathematics.

∗Foundation item:The National Natural Science Foundation of China(11561037);the Research Foundation of Educational Commission of Yunnan Province of China(2015z035).

†Corresponding author:Z.Luo.E-mail address:zql1009@126.com

doi:10.3969/j.issn.1005-3085.2016.03.010

Article ID:1005-3085(2016)03-0319-12

1 Introduction

The fluid motion in a tank has been investigated in past decades.Abramson[1],Ibrahim[2],Faltinsen and Timokha[3]provided a coherent and systematic introduction to the theory of fluid dynamics.For early investigation,Miles[4],Faltinsen[5],Penney[6],Moiseyev[7],Hutton[8],and Whitham[9]investigated the fluid sloshing in a 2D tank and presented some hydrodynamics results.With the rapid development of numerical methods,the finite element method,the boundary element method and the finite difference method have been employed to find the numerical solutions during the past decades.Wu and Chen[10-12]studied the wave elevation of the free surface and the excited frequency base on a time-independent finite difference method.Wuet al[13]considered the phenomenon of liquid sloshing in a 3D tank with various damping devices by the time-independent finite difference method combined with the ghost(fictitious)cell approach.Ebrahimianet al[14]presented a developed successive boundary element method to determine the symmetric and antisymmetric sloshing natural frequencies and mode shapes for multi baffled axisymmetric containers with arbitrary geometries.Guoet al[15]applied the finite volume particle(FVP)method to validate three-dimensional sloshing dynamics with a free surface by comparing with results from experiments.Ma and Karniadakis[16]studied the stability and dynamics of three-dimensional limit-cycle states in flow past a circular cylinder using low-dimensional modelling.Xue and Lin[17]developed a three-dimensional(3-D)numerical model NEWTANK to study viscous liquid sloshing in a tank with internal baffles of different shapes and arrangements.

The present paper is devoted to the numerical simulation of wave elevation for incompressible Navier-Stokes equations.The wave elevation on the free surface decays with different Renolds number and excited frequencies.

2 Physical model

First,a physical model in a two dimensional tank is presented.The conversation Navier-Stokes equations are denoted with the following scheme

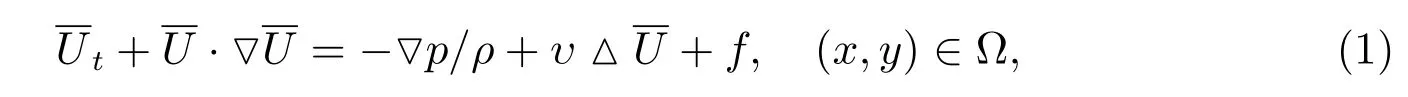
where f is body force,f=(fx,fy)T,fx=−ax,fy=−g−ay,Ω is fluid domain,the velocity is,ρis the density of the fluid,axandayare the excited accelerations,gis the gravity acceleration,υis the viscous coefficient of the fluid.

The continuity equation is written as

The free surface boundary condition is

whereη(x,t)is measured from the tank base to the undisturbed free surface andh=η+dis the wave elevation,ddenotes the height of the fluid in Figure 1.

The fluid pressure is denoted as

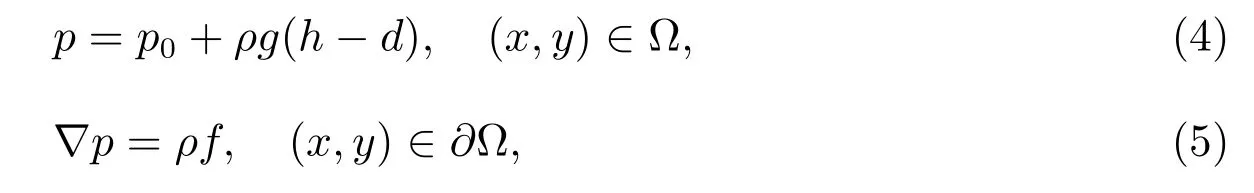
wherep0is the pressure of the free surface.

Figure 1:Coordinate transformation

From the partial differential equation(1),we can obtain the following Poisson equation

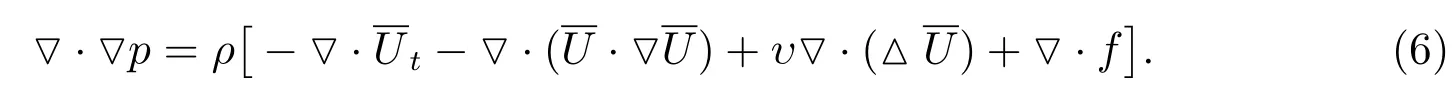
The no-slip boundary condition between the fluid and the wall is written as

The dynamic condition requires that,along the free surface boundary,the normal stress be equal to the atmospheric pressure and that the tangential stress be zero[18]

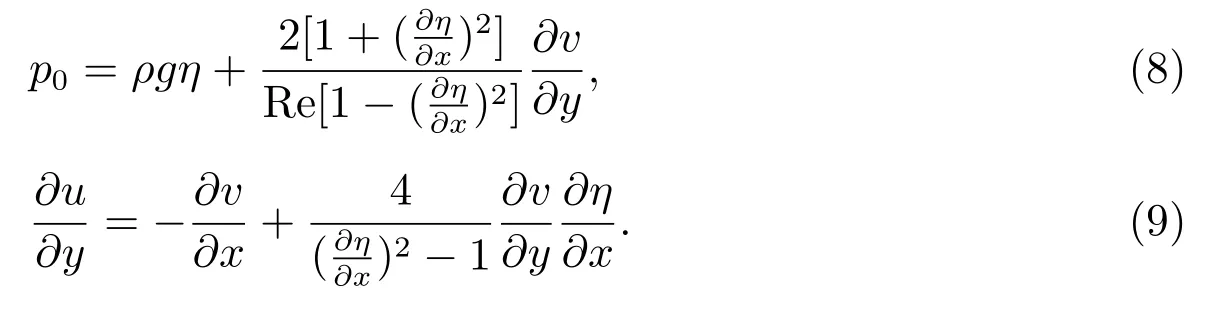
3 Dimensionless of Navier-Stokes equations

The fluid in the tank in Figure 1(a)can be transformed onto a regular square domain with unit cells by the following coordinate transformations:

here,b1andb2are the boundary condition on the left wall and the right wall,respectively.

To present the dimensionless Navier-Stokes equations,we set a few characteristic schemes

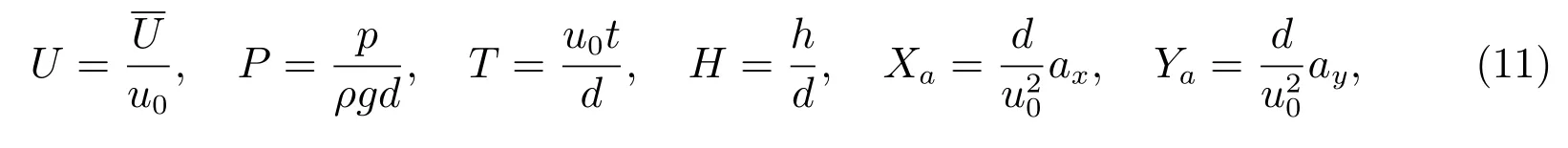
whereu0is characteristic velocity,U=(U1,V1).By employing these formulas(11),we have the dimensionless Navier-Stokes equations

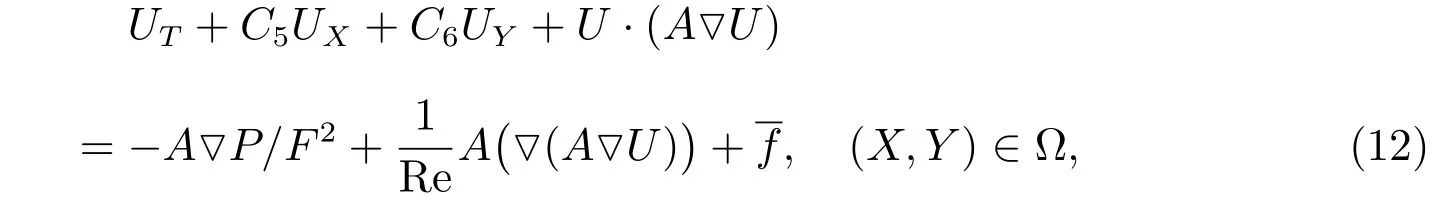
here

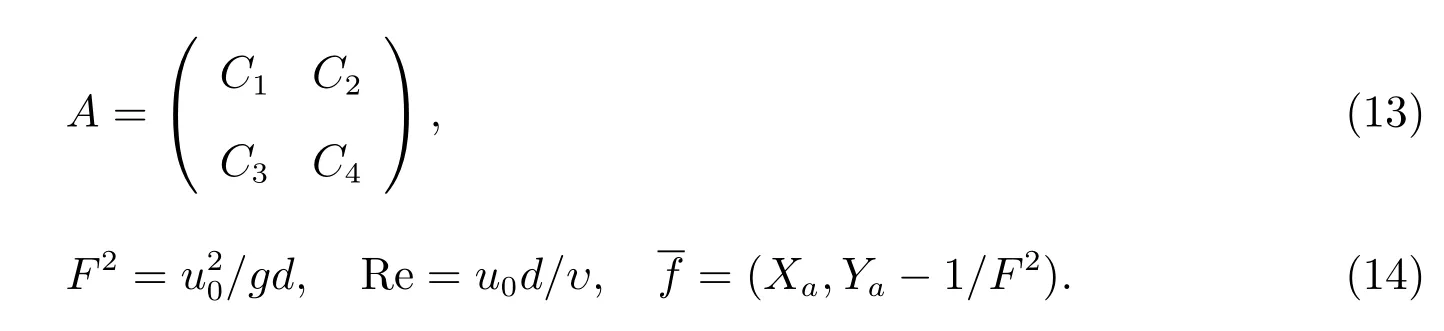
The dimensionless continuity equation is denoted by

where∗is the Hadamard product,B=(C1,C3,C2,C4).

The free surface condition is rewritten as

where·denotes the inner product.

The dimensionless pressure equation is written as

where

The coefficients are

The dimensionless dynamic boundary condition(8),(9)on the free surface are rewritten as

4 Finite difference method of Navier-Stokes equations

The fi nite difference method for Navier-Stokes equations in a two dimensional tank is designed with the Crank-Nicolson scheme[19].Since the staggered grid can avoid the jagged edge[20],the computational domain is divided with the staggered grid.Figure 2(a)shows the location of the variablesand pressure p in the cell grids,which are consisted of the computational grids in Figure 2(b).

Figure 2:Staggered grid system

The Crank-Nicolson fi nite difference method for Navier-Stokes equations is presented in the following statements.The Navier-Stokes equations,the Poisson equation and the kinematic boudary equations are discreted with Crank-Nicolson shemes.The fi rst order derivative and the second order derivative are discreted with the central difference scheme.The superscriptnrepresents the time levelnΔT,the subscript(i,j)represents the spatial position(iΔX,jΔY).The time level)ΔTdenotes the mean values at the time(n+1)ΔTandnΔT.

The Navier-Stokes equations is discreted with the Crank-Nicolson fi nite difference method as follows

The kinematic boundary equation on the free surface is discreted with the Crank-Nicolson finite difference method

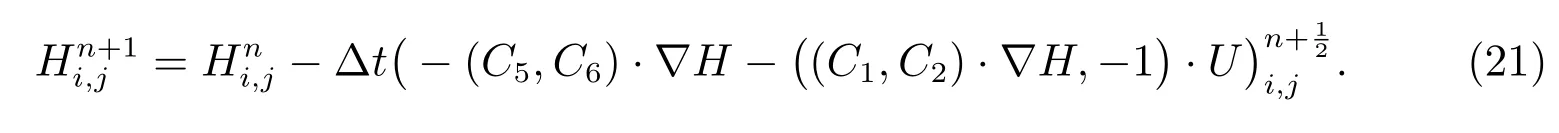
The pressure Poisson equation(17)is calculated with the successive over relaxation(SOR)method.For

hereai,jis the coefficient ofPi,j,ωis a relaxation factor.The pressure boundary conditions(4),(5)can be denoted as

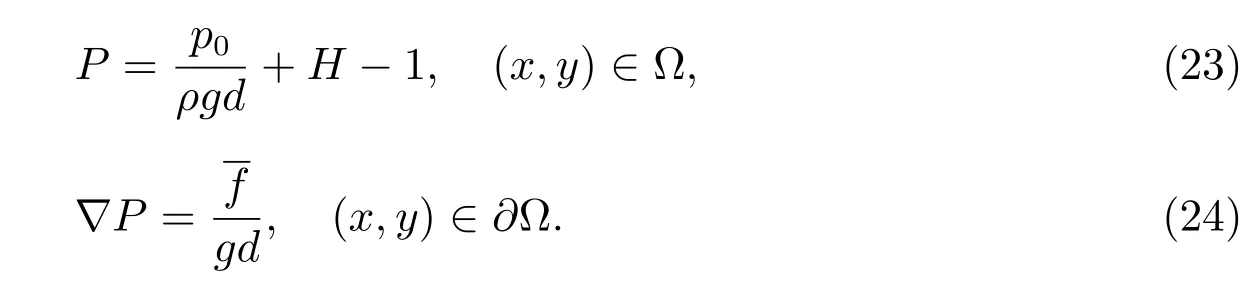
The stability condition[21]for Navier-Stokes equations is

5 Numerical algorithm of Navier-Stokes equations

The finite difference iterative algorithm of Navier-Stokes equations is presented in the following procedure.

(i)Set the initial valuesU,PandH.

(ii)ComputePfrom the scheme(22)with the convergence condition‖Pk+1−Pk‖∞＜10−6,kis an iterative number.

(iii)CalculateUfrom the scheme(20).If‖Uk+1−Uk‖∞＜10−6holds,then go to the next step;or else,go to step(ii).

(iv)ComputeHfrom the scheme(21).If‖Hk+1−Hk‖∞＜10−9holds,then stop the calculation;or else go to step(ii).

6 Numerical results

6.1 Benchmark test

In this section,we present the numerical simulation of free surface and fluid fields for incompressible Navier-Stokes equations.The numerical solutions are compared with previous published works.The long time history wave is simulated with different wave elevations parameters.The dissipative phenomenon and the wave elevation of excited wave is investigated in what follows.

The tank’s width in Figure 1 is(b2−b1)m,the fluid depth isdm.The tank base is divided intoMintervals,and the tank height is divided intoNintervals.The initial wave on the free surface isη0=Acos(knx),the dispersion relation is

The excited accelerations areax=X0sin(ωxt)anday=Y0sin(ωyt).

We first present the numerical solution of excited oscillation and compare this numerical solution with the previous published works.The tank width and the tank depth are set asb2−b1=0.9m,d=0.6m,X0=0.002m,ωx=5.5,Re=2000,the grid number(M,N)=50×20.From the Figure 3,the viscous numerical solution agrees well with the published work[21],so the present finite difference method is very effective.

Figure 3: Wave elevation on the free surface at the right wall x=b2in 10 seconds.Solid line:The present solution;circle line:Chen bangfu’s solution

The second benchmark test is to validate the mesh grid resolutions of the present numerical solutions.Table 1 shows the errors between the analytical solutionsηanaland the numerical solutionsηnumerat the left and right walls on the free surface in 6 seconds.As shown in Table 1,the errors decrease as the mesh grid numbers(M,N)increase.

Table 1: Error values of analytic solutions Hanaland numerical solutions Hnumerin 6 seconds

6.2 Numerical solutions

We investigate the long-time history of the excited wave.The parameters areb2−b1=1.0m,d=0.5m,X0=0.001m and(M,N)=(50,40).The different excited frequencyωxand Re are presented in the following tests.

Figure 4,Figure 5 and Figure 6 show dissipative wave withωx=0.6ω1,0.9ω1,0.96ω1,and Re=8000.From the Figure 4,Figure 5 and Figure 6,the wave elevation of the dissipative wave decreases obviously.The beating periods is very clear,and the wave crest decreases slowly in Figure 5 and Figure 6 as a result of the effect of the viscosity.

Figure 4:Wave elevation at x=b1,Re=8000,ωx=0.6ω1in 60 seconds

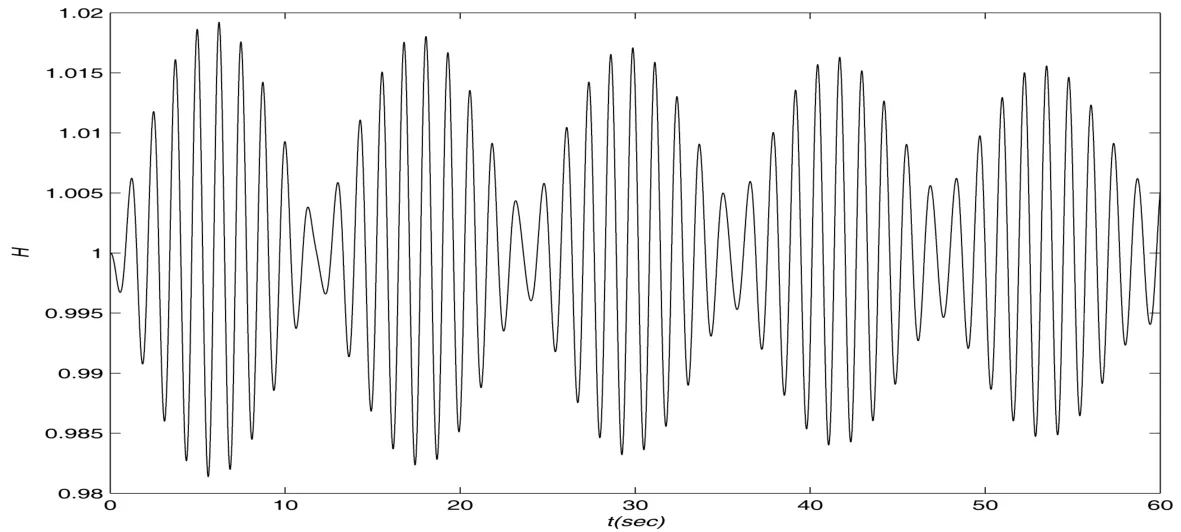
Figure 5:Wave elevation at x=b1,Re=8000,ωx=0.9ω1in 60 seconds

Figure 6:Wave elevation at x=b1,Re=8000,ωx=0.96ω1in 60 seconds

We consider the Reynolds number Re=2000,the parametersωx=0.6ω1,0.9ω1and 0.96ω1.When the Reynolds number decreases,the viscous effect increases.The wave elevation of the free surface decreases obviously between the Figure 4 and Figure 7.The beating period in Figure 5 can be seen obviously,but the amplitude of the wave decreases tinily.From the Figure 8,the beating period of wave disappears gradually as a result of viscous effect,and the beating period is not change between the Figure 5 and Figure 8.As shown in the Figure 6 and Figure 9,the number of the beating period is same and the Figure 6 exists two beating periods.Figure 9 exists only one beating period,the second beating amplitude has been decayed owing to a relative physical viscous effect.The dissipative effect for the small Reynolds number is far greater than the large Reynolds number.

Figure 7:Wave elevation at x=b1,Re=2000,ωx=0.6ω1in 60 seconds

Figure 8:Wave elevation at x=b1,Re=2000,ωx=0.9ω1in 60 seconds

Finally,we select the small Reynolds number Re=500 andωx=0.6ω1,0.9ω1and 0.96ω1,respectively.When the viscous effect become strong,the dissipative phenomenon become evidently.From these Figure 10,Figure 11 and Figure 12,we find that the number of the beating periods decrease between the Figure 8 and the Figure 11,the other fi gures have similar results between the Figure 9 and the Figure 12.The beating phenomenon does not appear in Figure 4,Figure 7 and Figure 10,because the excited frequencyωxis far away from the natural circle frequencyω1.We can fi nd the wave elevations decrease in Figure 4,Figure 7 and Figure 10.From the Figure 10,Figure 11 and Figure 12,we can fi nd that the free surface decays gradually and fi nally the free surface keep a stable elevation due to the balance between the excited acceleration and viscous effect.

Figure 9:Wave elevation at x=b1,Re=2000,ωx=0.96ω1in 60 seconds

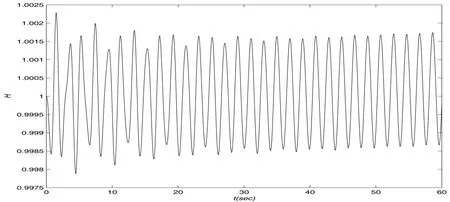
Figure 10:Wave elevation at x=b1,Re=500,ωx=0.6ω1in 60 seconds

Figure 11:Wave elevation at x=b1,Re=500,ωx=0.9ω1in 60 seconds

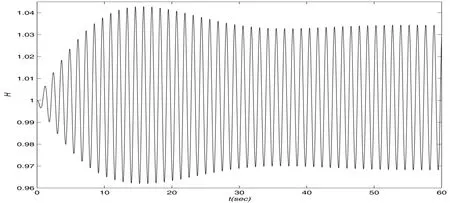
Figure 12:Wave elevation at x=b1,Re=500,ωx=0.96ω1in 60 seconds

7 Conclusions

A time-dependent finite difference method for incompressible Navier-Stokes equations is developed and is used to find the numerical solution of the free surface in a two dimensional tank.We investigate the wave elevation on the free surface with the different excited accelerations and Reynolds numbers.From the numerical results,we can find the wave elevations decay gradually along with the time.The number of the beating periods diminish as the Reynolds number diminishes.Finally,we find that the wave elevation on the free surface will keep a related stable height,when the Reynolds number diminish in Figure 10,Figure 11 and Figure 12.

References:

[1]Abramson H N.The dynamic behavior of liquids in moving containers[R].NASA Special Reports,SP-106,National Aeronautics and Space Administration,Washington D.C.,1966

[2]Ibrahim R A.Liquid Sloshing Dynamics,Theory and Applications[M].Cambridge:Cambridge University Press,2005

[3]Faltinsen O M,Timokha A N.Sloshing[M].Cambridge:Cambridge University Press,2009

[4]Miles J W.Nonlinear resonant surface waves in a circular cylinder[J].Journal of Fluid Mechanics,1976,75:419-448

[5]Faltinsen O M.A nonlinear theory of sloshing in rectangular tanks[J].Journal of Ship Research,1974,18(4):224-241

[6]Penney W G,Price A T.Finite periodic stationary gravity waves in a perfect liquid[J].Philosophical Transactional of the Royal Society of London,Series A,1952,224(882):254-284

[7]Moiseyev N N.On the theory of nonlinear vibrations of a liquid of finite volume[J].Applied Mathematics and Mechanics,1958,22(5):612-621

[8]Hutton R E.An investigation of resonant nonlinear non-plannar free surface oscillations of a fluid[R].NASA TND-1870,1963

[9]Whitham G B.Non-linear dispersion of water waves[J].Journal of Fluid Mechanics,1967,27:399-412

[10]Wu C H,Chen B F.Sloshing waves and resonant modes of fluid in a 3D tank by a time independent finite different method[J].Ocean Engineering,2009,36(6-7):500-510

[11]Chen B F,Wu C H.Effects of excitation angle and coupled heave-surge-sway motion on fluid sloshing in a three-dimensional tank[J].Journal of Marine Science and Technology,2011,16(1):22-50

[12]Wu C H,Chen B F.Transient response of sloshing fluid in a three dimensional tank[J].Journal of Marine Science and Technology,2012,20(1):26-37

[13]Wu C H,Faltinsen O M,Chen B F.Analysis on shift of nature modes of liquid sloshing in a 3D tank subjected to oblique horizontal ground motions with damping devices[J].Advances in Mechanical Engineering,2013,2013(5):1-24

[14]Ebrahimian M,Noorian M A,Haddadpour H.A successive boundary element model for investigation of sloshing frequencies in axisymmetric multi baffled containers[J].Engineering Analysis with Boundary Elements,2013,37(2):383-392

[15]Guo L C,Zhang S,Morita K,et al.Fundamental validation of the finite volume particle method for 3D sloshing dynamics[J].International Journal for Numerical Methods in Fluids,2012,68(1):1-17

[16]Ma X,Karniadakis G E.A low-dimensional model for simulating three-dimensional cylinder[J].Journal of Fluid Mechanics,2002,458(1):181-190

[17]Xue M A,Lin P Z.Numerical study of ring baffle effects on reducing violent liquid sloshing[J].Computers Fluids,2011,52(30):116-129

[18]Huang C J,Zhang E C,Lee J F.Numerical simulation of nonlinear viscous wavefields generated by pistontype wavemake[J].Journal of Engineering Mechanics,1998,124(10):1110-1120

[19]Crank J,Nicolson P.A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type[J].Proceedings of the Cambridge Philosophical Society,1947,43(1):50-67

[20]John D Anderson.Computational Fluid Dynamics—The Basics with Applications[M].New York:McGraw-Hill Inc,1995

[21]Chen B F,Nokes R.Time-indenpendent finite difference analysis of fully nonlinear and viscous fluid sloshing in a rectangular tank[J].Journal of Computational Physics,2005,209(1):47-81