非均质表皮层径向双层承压井流数学模型的半解析解∗

王玉林,谢康和,黄大中,李传勋

(1-武夷学院土木工程与建筑学院，福建武夷山 354300;2-浙江大学软弱土与环境土工教育部重点实验室，杭州 310027;3-铁道第三勘察设计院集团有限公司，天津 300251;4-江苏大学土木工程与力学学院，镇江 212013)

1 引言

石油和地下水开采井在钻进和形成过程中井周土受到挤压、涂抹和污染作用使井周扰动土的渗透性低于未扰动土的渗透性，而形成“正表皮层”(positive skin)；另一方面，在抽取地下流体的生产过程中，由于井周涂抹层剥落、开裂或土层中的细微颗粒被带走使得井周土的渗透系数大于原有结构层的渗透性，而形成“负表皮层”(negative skin)[1-4]．井周表皮层厚度往往从几毫米到几米不等，在井流理论研究中，根据表皮层厚度或者是否考虑表皮层的弹性释水，建立了两种具有很大差异的两种数学模型进行渗流问题求解[1-3]．当表皮层厚度较薄或者不需要考虑表皮层弹性储水时，可引入表皮效应系数，建立径向单层井流模型进行地下渗流模拟[4,5]，而当表皮层厚度较大，需要考虑表皮层弹性储水时，应采用径向双层的井流模型才能准确的分析地下流体的渗流作用[1-3,6,7]．Yeh和Yang等学者对考虑表皮层弹性储水的径向双层井流模型理论进行较为深入的研究[1,6-8]．本文对已有的径向双层、各向同性承压完整井二维井流模型作了改进，考虑了表皮层各向异性及其径向渗透系数的竖向非均质性，考虑了未扰动承压含水层的各向异性以及竖向越流补给作用，建立相应的三维井流数学模型，通过Laplace变换和矩阵理论求得表皮层和未扰动承压层内水头降分布和井壁流量的半解析解，应用实例分析了表皮层和未扰动承压层的渗透性对水头降和井流量的影响．

2 数学模型

2.1 基本假设与渗流控制方程

对于表皮层为有限厚度，并且考虑其弹性储水的承压含水层完整井井流问题，Yeh和Yang等[1,6,7,9]引入了如下基本假设：

1)表皮层和未扰动承压层为均质、各向同性，含水层侧向无限延伸，表皮层等厚分布于井周；

2)抽水井为有限直径的完整井；

3)承压含水层初始水头为常数；

4)井周表皮层为有限厚度．

基于这些假设，他们建立了径向双层承压含水层的二维井流模型，其中表皮层和未扰动承压层的渗流控制方程为

其中sI,SsI和KIr分别为表皮层的水头降、比弹性释水系数(或贮水率)和径向渗透系数；sII,SsII和KIIr分别为未扰动承压层的水头降、比弹性释水系数(或贮水率)和径向渗透系数．

实际上，表皮层和未扰动承压含水层多为非均质、各向异性，并且承压地下水存在垂直方向的越流补给作用．据此，本文对Yeh和Yang的上述假设基础上作了改进，不仅考虑了表皮层各向异性及其径向渗透系数的沿井深方向(竖向)的非均质性，而且考虑了未扰动承压含水层的各向异性，以及弱透水层的越流补给作用，建立径向双层、各向异性承压含水层的三维井流数学模型，其控制方程为

其中KIr(z)为非均质性表皮层的径向渗透系数，它是关于z的函数；KIv和KIIv分别为表皮层和未扰动承压含水层的竖向渗透系数．为便于问题求解，根据表皮层径向渗透性沿井深方向的非均质性，将表皮层和未扰动承压层沿竖直方向(z方向)统一划分N层，并自上而下依次编号，这样可将原问题转化为径向为双层、竖向为N层的承压含水层系统井流概念模型，如图1所示．

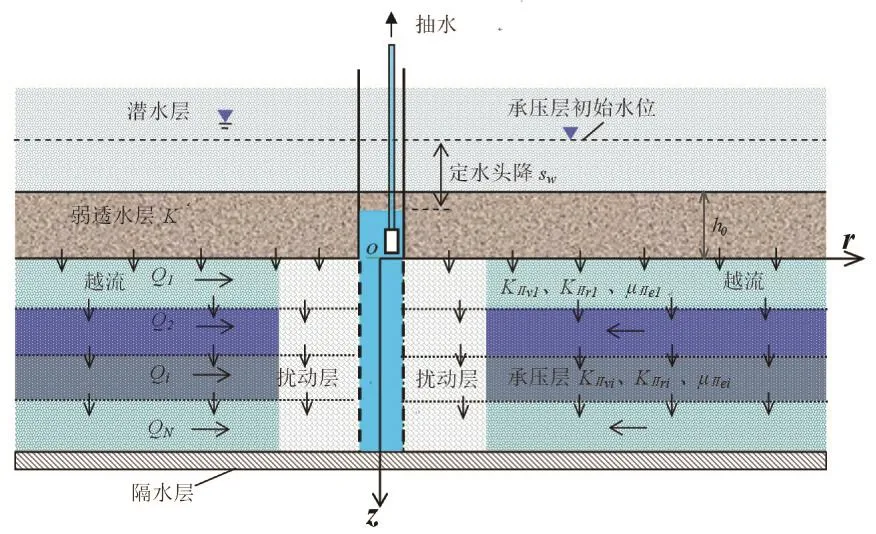
图1: 考虑非均质各向异性表皮层的径向双层承压层的井流概念模型

2.2 径向双层各向异性承压含水层非稳态井流的数学模型

根据上述假设与图1所示概念模型，可建立竖向N层越流系统中的表皮层和未扰动承压层的地下水三维渗流方程，其中N层表皮层(rw≤r≤rs)内的地下水三维渗流方程表达为

越流系统中N层未扰动承压层(rs≤r＜∞)内地下水三维渗流方程表达为

上式中sIi和sIIi分别为第i层表皮层和第i层未扰动承压层的水头降，假设上覆弱透水层无水头降sI0=sII0=0，底部隔水层有sIN=sIIN+1=0；TIi=KIrihi和TIIi=KIIrihi分别为第i层表皮层和未扰动承压层的水头传导系数；µeIi和µeIIi分别为第i层表皮层和未扰动承压层的弹性释水系数；

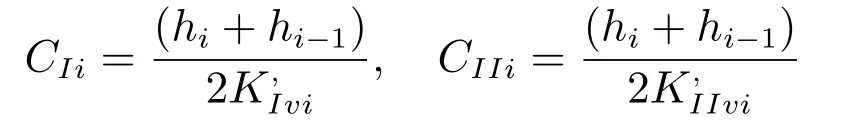
分别为表皮层和未扰动承压层在第i层与第i−1层间之间的阻力系数，特别地，CI1=，CII1=和CIN→∞；KIri和KIvi分别为第i层表皮层径向和竖向渗透系数，KIIri和KIIvi分别为第i层未扰动承压层径向和竖向渗透系数；hi为第i层土的厚度，h0为弱透水层厚度，i=1,2,3,···.

上述两方程组系统的求解条件：

(a)抽水井定降升边界条件：sIi(rw,t)=ssw；

(b)无限远处的自然边界条件：sIIi(∞,t)=0；

(c)表皮层和未扰动承压层之间的水头连续条件：sIi(rs,t)=sIIi(rs,t),t＞0；

(d)表皮层和未扰动承压层之间的流量连续条件：

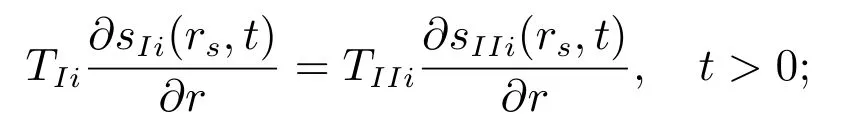
(e)初始条件：sIi(r,0)=sIIi(r,0),r＞rw；

其中sw为竖井内的降深，rw为抽水井半径，rs为表皮层外径．

3 问题求解

分别对方程组(5)和方程组(6)进行Laplace变换可得到线性常微分方程组，并用微分算子进一步简化成矩阵形式的常微分方程组，形如

其中∇2=为Laplace算子，I=[I1I2···IN]T为Laplace域内各层表皮层水头降组成的向量，II=[II1II2···IIN]T为Laplace域内各层未扰动承压层水头降组成的向量，A和B分别为表皮层和未扰动承压层的渗流控制方程对应的矩阵，均为N×N的方阵，其中A矩阵可写为

矩阵B的形式与矩阵A的形式一样，将矩阵A各元素中的下标I改为II即可得矩阵B．根据矩阵理论，容易求得矩阵A的N个特征值为：λI1,λI2,···,λIN，各特征值对应向量组成的向量矩阵为YI，B的N个特征值为：λII1,λII2,···,λIIN，对应向量组成的向量矩阵为YII．于是可利用A=YIλIYI−1和B=YIIλIIYII−1，将线性矩阵微分方程组(7)变为解耦形式的方程组

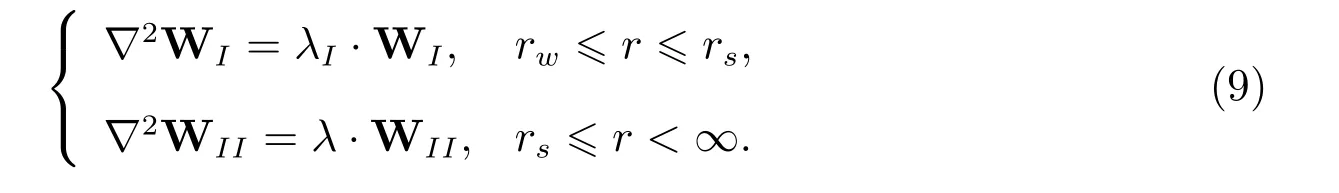
将方程组(9)结合表皮层和未扰动承压层中的渗流Laplace变换域求解条件，可得到表皮层和未扰动承压层水头降的Laplace域内一般解

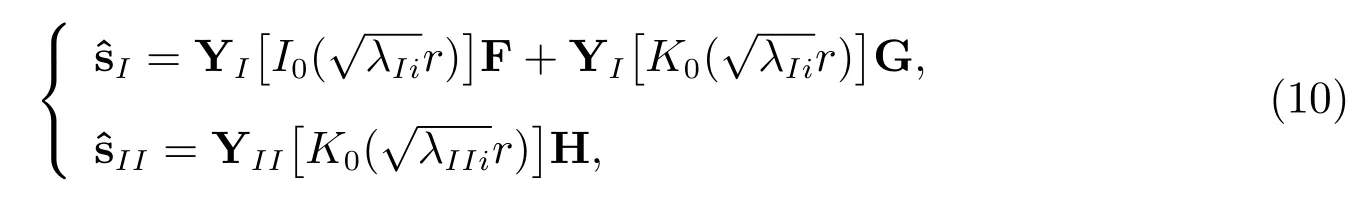
其中F,G和H为由边界条件确定的待定常数向量，因为未扰动承压层和表皮层沿着z方向划分N层，因此每个常数向量均含有N个分量；为以零阶修正Bessel函数为对角元素的对角方阵．

可由井周边界条件(a)得到

由表皮层和未扰动承压层边界上的水头连续条件(c)得到

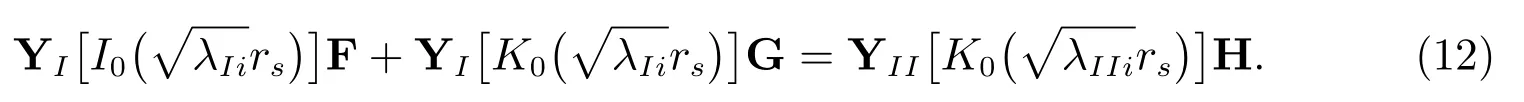
再由表皮层和未扰动承压层边界上的流量连续条件(d)得到

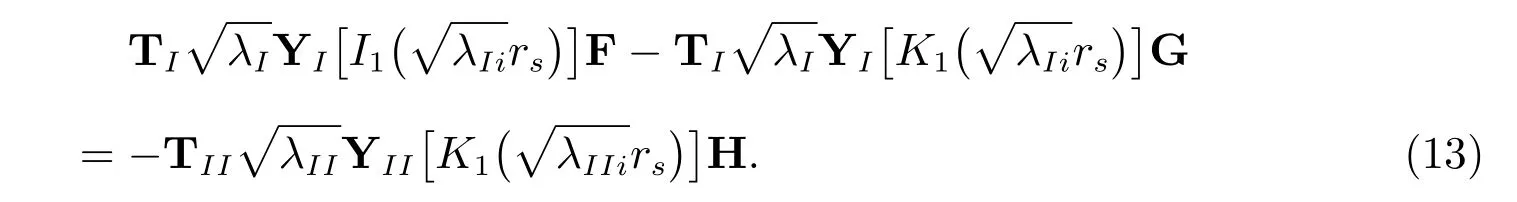
为了便于计算机的编程计算，将式(11)—(13)合并成矩阵的形式

可用数学软件程序求线性方程组(14)的解，即求得常数向量F,G和H：

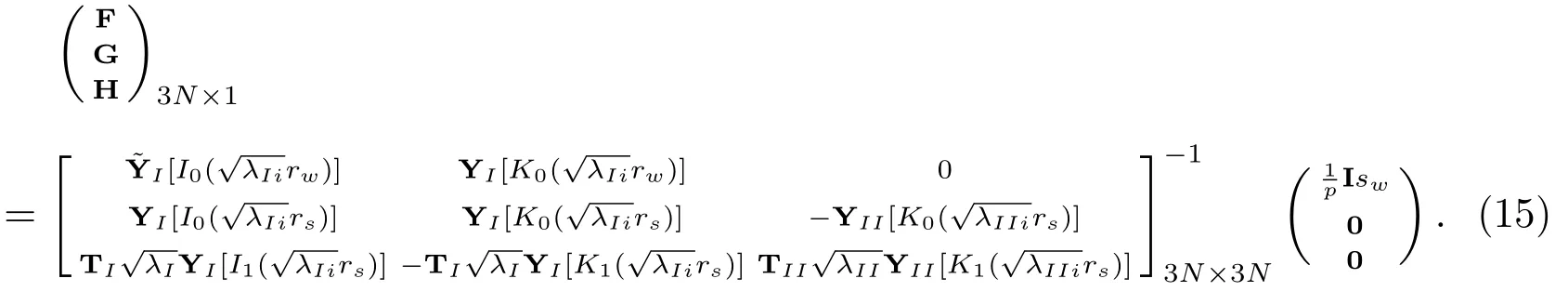
将求解得到的常数向量F,G和H代入式(10)，即可分别得到表皮层和未扰动承压层的水头降 Laplace域上的解I和II．

同样地，可对I关于变量r求导得到井周边界处r=rw各分层的流量

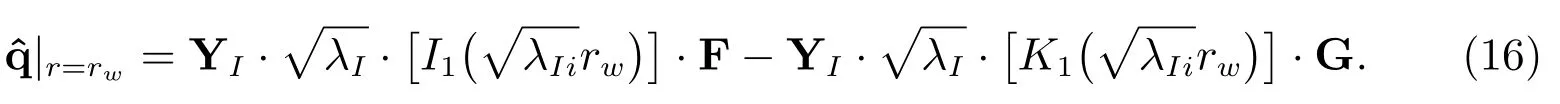
由于上述解较复杂，直接用Laplace逆变换求得物理域解析解表达式比较困难，因此，可采用Stefest数值反演方法求得时间域上的物理量[10]．

4 解的讨论

1)当未扰动承压层和表皮层均为均匀、各向同性时，即CIi,CIIi,µeIi,µeIIi,TIi以及TIIi各层相等，取为常数，则本文径向双层、竖向N层的承压含水层系统抽水井流问题退化为径向双层、竖向单层的承压含水层越流完整抽水井流问题[11]；进一步，当承压含水层上层为隔水边界，无越流补给时，即CIi→∞，则本文解可为考虑表皮层弹性释水的定降深承压井流问题的解[9]．

2)当考虑承压含水层的层状特性，但不考虑表皮效应时，即CI,CII和TI=TII，本文解退化为越流多层承压含水层系统井流解[12]．

3)当抽水时间较长时，即p→0，承压含水层中的地下水达到稳态流状态，此时对应的稳态流水头降解为

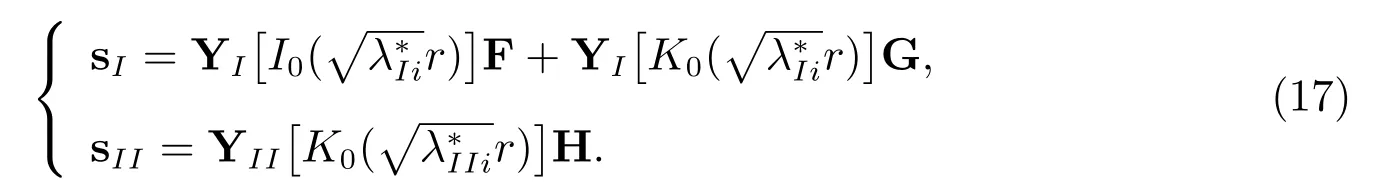
当承压含水层达到稳态流状态时，抽水井周各分层对应的流量分量为

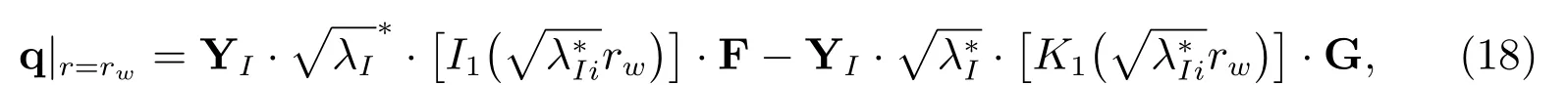
其中和分别为矩阵A和矩阵B中p→0时所求得的特征值．

5 表皮层非均质的径向双层各向异性承压层井流分析

应用数学软件编制计算程序，通过算例对径向双层各向异性承压含水层水头降和流量及影响因素进行分析．由算例得到的分析曲线图，坐标系物理量采用无量纲形式：水位降、竖井的抽水流量、径向坐标、竖向坐标．

在算例中，假设表皮层为层状非均质、各向异性的，径向渗透系数KIr沿竖井方向(z方向)层状随机变化，可用分段连续函数表示为：KIr(z)=βj(z)(βj(z)为第j段函数)，如图2所示，分段函数共7个分段(层数)，自上而下各层径向渗透系数的取值为

在计算过程中，将每一分段函数KIr(z)对应层位的层表皮层和非扰动承压层(zj−1≤z≤zj)再划分6层，因此，共划分成42层，取计算层中点位置处的数据绘制各相应图形．

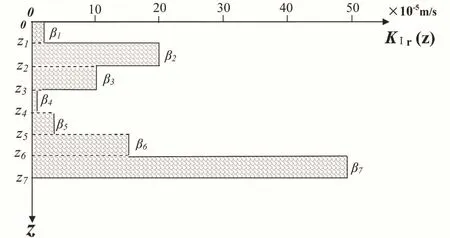
图2: 表皮层径向渗透系数KIr竖向层状随机变化示意图

5.1 承压含水层水头降沿竖向分布规律及影响因素分析

根据图2所示表皮层径向渗透系数KIr沿z方向的层状随机变化，绘制得到不同井距处承压含水层水头降沿竖向变化的曲线s∗−z∗，如图3所示，图中各计算点的位置分别为：r∗=10和r∗=100在表皮层内，r∗=300在表皮层和未扰动承压含水层交界面处，r∗=1000和r∗=1500在未扰动承压含水层内．

对比图3中不同r∗位置处的s∗−z∗曲线可知：在表皮层内以及在表皮层附近处，水头降沿竖向的变化趋势与图2中表皮层径向渗透系数KIr沿井深变化趋势具有较好的一致性，即，各层承压含水层的水头降随同层位表皮层径向渗透系数值βj的大小变化而变化，水头降沿竖向分布曲线随层位变化较明显，能够从水头降变化直观的反映出不同层位表皮层渗透性．但是，随着与表皮层距离增大，表皮效应逐渐减弱，承压含水层的水头降s∗−z∗曲线随表皮层分层变化的特征逐渐消失．

图3: 表皮层径向渗透系数KIr沿井深分层变化时不同井距处的水头降沿竖向分布s∗−z∗曲线

为研究表皮层对不同渗透性的各向异性承压含水层的影响，计算了四种渗透性的承压含水层的水头降，绘制得到在距井较近处(r∗=400)和距井较远处(r∗=1500)的s∗−z∗曲线，分别如图4和图5所示．

对比图4和图5可以知道：表皮层对承压含水层的影响范围与承压含水层的竖向渗透系数KIIv密切相关，即，承压含水层的竖向渗透系数KIIv越小(大)，表皮层对承压含水层渗流产生影响的范围就越大(小)，而且表皮效应越明显(不明显)．

图4: KIr沿在较小井距r∗=400处水头降沿竖向分布s∗−z∗曲线

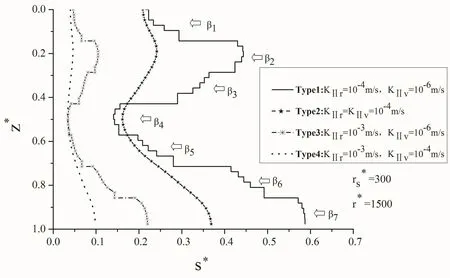
图5: KIr沿在较大井距r∗=1500处水头降沿竖向分布s∗−z∗曲线

具体分析来看，承压含水层竖向渗透系数较小时(KIIv=10−6m/s)，在距井较近处(r∗=400)和较远处(r∗=1500)水头降沿竖向的分布形态均与图2中的表皮层径向渗透系数KIr沿井深层状变化有较好的一致性，水头降较明显地随表皮层的层位不同而变化，表明：KIIv较小时，在较远处承压含水层地下水仍受到较强的表皮效应作用；然而，当竖向渗透系数较大时(KIIv=10−4m/s)，仅在距井较近处(r∗=400)水头降沿竖向的分布形态才与表皮层径向渗透系数KIr的层状变化有较好的一致性，而在距井较远处(r∗=1500)水头降沿竖向的分布形态不再具有与表皮层对应的层状性，表明：KIIv较大时，在较远处承压含水层地下水受表皮效应的作用不明显．

产生上述现象的原因在于：承压含水层竖向渗透系数KIIv较小时，上下相邻层之间的越流较弱，各层中的地下水渗流受竖向水流干扰较小，而受同层位表皮层的影响较强，因此水头降沿竖向的分布形态能较明显地与表皮层的层状性对应；但是，当承压含水层竖向渗透系数KIIv较大时，上下相邻层之间的越流较强，各层中的地下水渗流受竖向水流干扰较大，而受同层位表皮层的影响较弱，因而水头降沿竖向的分布形态不再与表皮层的层状性对应．

5.2 井壁流量分布规律及影响因素分析

图6为不同表皮层厚度对井壁处流量Q∗−z∗分布曲线的影响．该图表明：

1)表皮层的层状性导致水流量沿抽水井井壁非均匀分布，流量沿井深变化趋势与表皮层径向渗透系数变化趋势一致，表皮层径向渗透系数值βj越大的层位，相应位置处井壁的水流量就越大，反之则小；

2)对表皮层厚度的影响而言，有正、负表皮效应之分，在“正表皮层”层位处，表皮层的厚度越大，则相应层位处井壁的水流量越小，而“负表皮层”层位处，表皮层的厚度越大，则相应层位处井壁的水流量也越大．

由此可以看出，在定降深条件下，可通过增大表皮层渗透系数或增大“负表皮层”厚度提高抽水井产量，因此改善井周岩土介质渗透性或设置渗透性大于承压含水层渗透性的围填材料，对产量增加具有明显的效果．

图6: 不同厚度表皮层对井壁流量分布Q∗−z∗影响的比较

图7 为四种各向异性承压含水层的井壁水流量Q∗−z∗分布曲线．对比表皮层不同层位处对应的井壁流量(产量)可看出：表皮层径向渗透系数越大，不同渗透性的承压含水层之间井流量(或产量)的差别越大，承压含水层的渗透性对流量(或产量)影响就越大，因此承压含水层的渗透性(包括径向渗透系数KIIr和竖向渗透系数KIIv)对抽水井流量(或产量)的影响与表皮层径向渗透系数有关．就具体分析来看，第1、4和5层表皮层的径向渗透系数值较小，这些层位处各种承压含水层之间的流量差异较小，相应的Q∗−z∗曲线接近重合，而其他层位处表皮层的径向渗透系数值较大，各种承压含水层之间的流量差异也较大，相应的Q∗−z∗曲线明显分离．从总体上来看，七层表皮层的径向渗透系数值从小到大排列为β1,β2,β3,β4,β5,β6,β7，各层位处四种不同承压含水层的Q∗−z∗曲线的分离程度随βj值增大而增大，说明承压含水层的渗透性对井壁流量Q∗(产量)的影响随表皮层的径向渗透系数βj值增大而增大．

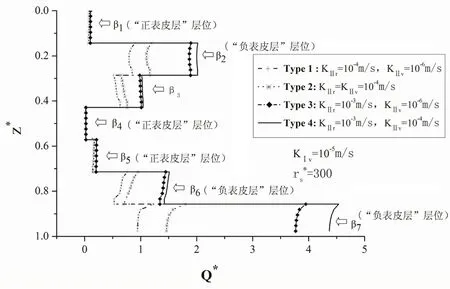
图7: 不同类型各向异性承压层的井壁流量分布s∗−z∗影响的比较

5.3 承压含水层和表皮层的渗透性对水头降径向分布s∗−r∗的协同影响

根据图2所示表皮层径向渗透系数KIr沿井深的分布模式，对五种不同承压含水层的水头降沿径向分布进行计算，取其中表皮层径向渗透系数KIr为较小值的层位(即顶层)和较大值的层位(即底层)的水头降曲线进行比较分析，如图8和图9所示．对比图8和图9水头降曲线可知：

1)不管表皮层的径向渗透系数值较小(β1)还是较大(β7)，水头降幅值均随着承压含水层渗透系数(包括径向渗透系数KIIr和竖向渗透系数KIIv)减小而增大；

2)表皮层径向渗透系数KIr较小值时(如：β1=10−5m/s)，承压含水层的水头降幅度主要取决于承压含水层径向渗透系数KIIr的大小，承压含水层竖向渗透系数KIIv对承压含水层水头降影响较小．这容易从图8看出，对于承压含水层竖向渗透系数KIIv相同，径向渗透系数KIIr不同的任意两条曲线，水头降差异均较大，但是对于承压含水层径向渗透系数KIIr相同，竖向渗透系数KIIv不同的任意两条曲线，水头降差异均较小；

3)表皮层径向渗透系数KIr的值为较大时(如：β7=50×10−5m/s)，承压含水层径向渗透系数KIIr和竖向渗透系数KIIv均对承压含水层的水头降有较大影响．这容易从图9看出，对于承压含水层竖向渗透系数KIIv相同，而径向渗透系数KIIr不同的任意两条曲线，水头降差异较大，若对比承压含水层径向渗透系数KIIr相同，而竖向渗透系数KIIv不同的两条曲线，水头降差异均较大；

4)同一承压含水层水头降曲线s∗−r∗在交界面处是呈向上折趋势，还是呈下折趋势，由所在层位的表皮层的负、正表皮效应性质决定．

图8: 表皮层KIr取值较小为β1=10−5m/s时五种承压含水层s∗−r∗曲线比较

图9: 表皮层KIr取值较大为β7=50×10−5m/s时五种承压含水层s∗−r∗曲线比较

6 结论

本文改进了Yeh和Yang的径向双层、各向同性承压完整井二维井流模型，考虑表皮层和未扰动承压层的非均质和各向异性以及层间的竖向越流补给作用，通过将表皮层和未扰动承压层沿竖向划分为有限层，建立了径向双层竖向有限层的三维井流数学模型，采用Laplace变换和矩阵理论求得承压含水层水头降和井壁流量的半解析解，通过算例分析得到如下结论：

1)在表皮层内以及在表皮层附近处，水头降沿竖向的变化趋势与表皮层径向渗透系数KIr变化趋势具有较好的一致性，而在远处表皮效应逐渐减弱，承压层水头降随表皮层分层变化的特征逐渐消失；

2)承压含水层的竖向渗透系数KIIv越小(大)，表皮层对承压含水层渗流产生影响的范围就越大(小)．原因在于：承压含水层竖向渗透系数KIIv大小决定竖向各分层之间越流强弱，进而影响表皮效应的强弱；

3)流量沿井深变化趋势与表皮层径向渗透系数变化趋势一致，通过改善井周岩土介质渗透性或增大“负表皮层”厚度可提高抽水井产量；

4)表皮层径向渗透系数KIr越大，不同渗透性承压含水层之间的井流量(或产量)差别越大，承压含水层的渗透性对流量(或产量)影响就越大；

5)表皮层径向渗透系数KIr为较小值时，承压含水层的水头降幅度主要取决于承压含水层径向渗透系数KIIr的大小，而承压含水层竖向渗透系数KIIv对承压含水层水头降影响较小；但是当表皮层径向渗透系数KIr较大时，承压含水层径向渗透系数KIIr和竖向渗透系数KIIv均对承压含水层的水头降有较大影响．

参考文献：

[1]Zhang W,Zhan H B,Huang G H,et al.Constant-head test in a leaky aquifer with a finite-thickness skin[J].Journal of Hydrology,2011,399(3):326-334

[2]Chen Y J,Yeh H D.Parameter estimation/sensitivity analysis for an aquifer test with skin effect[J].Ground Water,2009,47(2):287-299

[3]Yan S Y,Yeh H D.Laplace-domain solutions for radial two-zone flow equations under the conditions of constant-head and partially penetrating well[J].Journal of Hydraulic Engineering,2005,131(3):209-216

[4]Chen C S,Chang C C.Well hydraulics theory and data analysis of the constant head test in an unconfined aquifer with the skin effect[J].Water Resources Research,2003,39(5):1121-1135

[5]Chen C S,Chang C C.Theoretical evaluation of non-uniform skin effect on aquifer response under constant rate pumping[J].Journal of Hydrology,2006,317(3):190-201

[6]Yeh H D,Yang S Y,Peng H Y.A new closed-form solution for a radial two-layer drawdown equation for groundwater under constant-flux pumping in a finite-radius well[J].Advances in Water Resources,2003,26(7):747-757

[7]Yeh H D,Yang S Y.A novel analytical solution for a slug test conducted in a well with a finite-thickness skin[J].Advances in Water Resources,2006,29(10):1479-1489

[8]Yeh H D,Chen Y J,Yang S Y.Semi-analytical solution for a slug test in partially penetrating wells including the effect of finite-thickness skin[J].Hydrological Processes,2008,22(18):3741-3748

[9]Yan S Y,Yeh H D.Solution for flow rates across the wellbore in a two-zone confined aquifer[J].Journal of Hydraulic Engineering,2002,128(2):175-183

[10]Stehfest H.Remark on Algorithm 368:numerical inversion of Laplace transforms[J].Communications of the Association for Computing Machinery,1970,13(10):624-625

[11]Perina T,Lee T C.General well function for pumping from a confined,leaky,or unconfined aquifer[J].Journal of Hydrology,2006,317(3):239-260

[12]Hemker C J.Transient well flow in leaky multiple-aquifer systems[J].Journal of Hydrology,1985,81(1):111-126