基于代数决策图的贝叶斯网络参数简化技术∗

王 瑶,孙 秦

(西北工业大学航空学院，西安 710072)

1 引言

贝叶斯网络推理是在一个不确定性环境和不完全信息下进行决策支持和因果发现的工具．由于有坚实的概率论和图论理论基础，同时又可以很好地同专家知识进行融合，贝叶斯网络推理近年来已成为人工智能、模式识别、专家系统等领域的研究热点[1]．

贝叶斯网络推理方法可以分为两类：精确推理和近似推理．比较经典的精确推理算法有变量消元算法、联结树算法、图简约算法和多树传播算法[1,2]．近似算法有随机抽样、基于搜索的算法等．目前，这些算法均是用一张概率条件表来表示网络中的参数进行推理运算的，然而，条件概率表不能捕捉到网络参数呈现出的环境独立特点[3]．代数决策图是一种有效的数据表达形式[4]，它可以捕捉到网络参数环境独立的特点．因此，本文采用代数决策图取代条件概率表来表示网络参数，提出了条件概率表到代数决策图的转化方法，同时给出了转化的算法．

2 贝叶斯网络推理

贝叶斯网络推理问题可以归结为，在已知证据变量和网络结构的基础上，求解感兴趣变量的后验概率问题．数学描述如下：

对任意变量全集为N={X1,···,Xn}，联合概率分布为Pr(X1,···,Xn)的贝叶斯网络N，存在三类变量，证据变量E=e，查询变量Q，及其它无关变量S=N(Q∪M)；后验概率问题就是求概率分布Pr(Q|E=e)．根据文献[1]中的第二、三章，利用条件独立和链式法可得

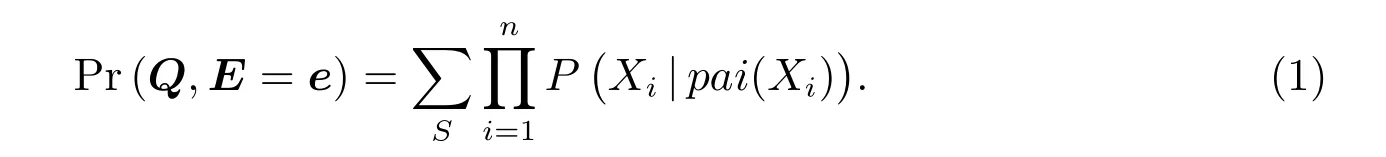
继而根据贝叶斯定理，计算

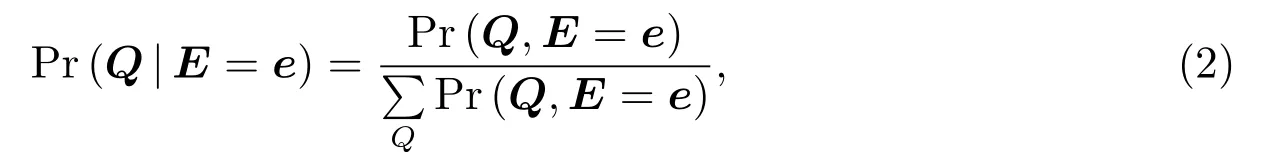
后验概率问题可解[1,2]．上式中pai(Xi)表示贝叶斯网络中任意节点Xi的父节点，P(Xi|pai(Xi))为节点Xi对应的条件概率分布(简称CPD)．

CPD用于描述父子节点依赖关系，其可用一张条件概率表表示(简称CPT)．CPT中各行数据表示已知父节点状态，子节点对应状态的发生概率．例如，图1中节点Z的CPD以CPT形式给出，该CPT第1行数据含义为：当父节点{X=0,Y=0}时，子节点Z=0的概率为0.1．类似于节点Z，图1中网络的其它节点T、X、Y和A也存在描述其与父节点依赖关系的CPT．根据贝叶斯网络定义[1]，贝叶斯网络每个节点均对应唯一的CPD(类似于图1，CPD通常用CPT表示)，找出网络证据变量集合E，并设置其等于已知变量e=E后，将所有节点的CPD(P(Xi|pai(Xi)))按照节点对应关系进行乘法计算，即可获得网络变量全集各状态的概率取值Pr(Q,S,E=e)．利用贝叶斯网络边缘化操作[1]消去变量集合S，即可获得已知E=e时变量集合Q的概率分布Pr(Q,E=e)．其中，依照节点对应关系进行乘法计算指的是，网络中参数相乘必须是在节点状态相同的情况下进行，例如在图1中，若对节点Z和节点T的CPDP(Z|Y,X)和P(T|A,Z)相乘，鉴于两节点的CPD中存在公共节点Z，因此必须在Z状态相同的原则下对两节点CPD中数据进行乘法运算，因此节点Z的CPT第1、3、5、7行数据只能分别与节点T的CPT前4行数据相乘，而不能与节点T的CPT后4行相乘法；同时节点Z的CPT第2、4、6、8行数据只能分别与节点T的CPT后4行数据相乘，而不能与节点T的CPT前4行数据相乘．此外，上述边缘化操作的实质为通过加法运算消去其它无关变量集合S，边缘化操作具体步骤为：对于通过乘法运算获得的概率分布Pr(Q,S,E=e)，当Q=q时，找出S各状态的对应概率取值并进行累加得到Pr(Q=q,E=e)；类似的，对Q所有状态，进行如上方式的累加以获得累加值；各累加值即构成概率分布Pr(Q,E=e)．例如已知图1中{X=1,Y=1}为证据变量，通过对各节点的CPT进行相乘可获得条件概率分布Pr(Z,A,T|X=1,Y=1)，该条件概率分布亦可用CPT表示，具体形式与图1中节点T的CPT形式完全相同．若其它无关变量集合S={A,Z}，那么将类似节点T的CPT中第1、3、5和7行概率值相加即可获得Pr(T=0,X=1,Y=1)；将CPT中第2、4、6和8行概率值相加即可获得Pr(T=1,X=1,Y=1)；概率值Pr(T=0,X=1,Y=1)和Pr(T=1,X=1,Y=1)构成最终结果Pr(T,X=1,Y=1)．

(1)和(2)是贝叶斯网络所有精确推理算法的依据[1]，其算法核心为CPD的存储以及与CPD之间的乘法、加法运算．

图1:贝叶斯网络示意图

3 条件概率分布的表示

3.1 环境独立

环境独立是指在特定环境下才成立的条件独立关系．一个环境(context)是一组变量及其取值的组合．张连文和郭海鹏[1]给出环境独立概念如下：

定义1设X,Y,Z,C是4个两两交集为空的变量集合，C的取值是c．如果当P(Z,Y,C=c)＞0时，P(X|Z,Y,C=c)=P(X|Z,C=c)成立，则称在环境C=c中，X与Y在给定Z时相互条件独立．更进一步，若Z为空，则称在环境C=c中，X与Y相互独立．

例如图2(a)中，有P(Z|Y,X=0)=P(Z|X=0)成立，Y与Z在环境X=0下相互独立．

环境独立是贝叶斯网络概率参数特征的体现．根据参数的特点，贝叶斯网络参数数据可以减少，故一定程度上可以提高推理效率．

3.2 条件概率表与代数决策树

依据贝叶斯网络的定义，贝叶斯网络的每个节点X都对应一个CPD，它存储了各节点与其父节点的依赖关系．所谓依赖关系，简而言之，就是在父节点状态已知情况下，子节点各状态的取值概率．直观的讲，就是“穷举各父节点状态下，子节点取各种状态的概率大小”．而表格很适用于状态穷举，故贝叶斯网络各节点用条件概率表(CPT)的形式表达、存储CPD中的上述依赖关系．但对于很多贝叶斯网络，节点条件概率参数之间存在了大量的环境独立情况[3]，子节点与父节点的依赖关系并不需要状态穷举，因此CPT的状态穷举存储方式将因不能捕捉到网络概率参数环境独立的特点而会带来冗余数据的不必要存储．例如，对网络任意节点X，其CPDP(X|pai(X))若CPT表示，则需穷举父节点与子节点的所有状态组合，且CPT中的条件概率数目将随父节点数目呈指数级别增长[1,3]，例如图2(a)中P(Z|Y,X)对应的条件概率表列举了父节点Y，X与子节点Z的所有8种状态组合及其对应概率参数．

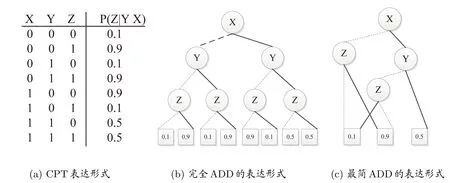
图2: 同一概率分布P(Z|Y,X)的三种不同表达形式

鉴于OBDD(ordered binary decision diagram)能够通过判断并消除结构中的冗余节点(冗余节点的判断实质为对独立信息的判断)而使得网络节点信息的存储达到最简单[5]，本文采用一种与OBDD类似的代数决策图(ADD)来取代CPT对网络概率参数进行存储，并通过消除ADD冗余节点完成贝叶斯网络各节点CPD的最简表达．例如，图2(c)中概率参数用ADD存储只需要存储5个(注意不是3个)，而不是CPT形式的8个．

下面，首先对ADD的基本概念进行论述，为后续最简ADD构造方法的提出提供理论基础．

与OBDD类似，ADD与OBDD的非叶节点均为表示变量的节点，例如X、Y等．两种图形的唯一区别在于：ADD的叶节点为概率数据，而OBDD叶节点仍为表示变量节点．唯一的区别意味着若将ADD中概率值相同的子节点合并视为一个变量，则OBDD与ADD完全相同，那么OBDD的理论则完全适用于ADD．具体来讲，ADD实质上是一个仅有一个根节点的有向无环图．每个非叶节点X为二元变量，虚线指向左孩子，表示X=0，实线指向右孩子，表示X=1．叶节点表示一个实数．在贝叶斯网络中，ADD的叶节点表示概率值．

从根节点到一个叶节点称为ADD的一条路径，每条路径变量出现的顺序必须保持一致，但不要求每个变量一定要出现．例如，图2(c)的ADD的变量排列顺序为X,Y,Z，从X到0.1有{X=0,Z=0}和{X=1,Y=0,Z=1}，前一条路径表示了图2(a)中第1、3行数据，后一条路径表示第6行数据．需要注意两点：

1)不同的变量顺序会有不同的ADD对应；

2)相同的变量顺序也可能会有不同的ADD对应．而这些不同的ADD的“最简形式”和“完全形式”却是一致的[5]．图2中，与(a)对应的(b),(c)分别为完全形式和最简形式．

用ADD表示贝叶斯网络中的概率参数存在以下两个意义．首先，ADD能更加简洁的表示贝叶斯网络中的因子．其最坏的情况下也不会多于CPT表的概率数量．其次，ADD有一套高效的运算规则[3]，包括乘法和加法．

4 算法实现与案例分析

4.1 CPT到ADD算法实现与验证

对于一般给定的贝叶斯网络，其条件概率分布一般均是以条件概率表的形式给出．那么，如何将条件概率表转化为最简ADD，成为利用ADD进行贝叶斯网络推理的前提和关键．

从第2节图2可知，一个直接的做法是首先为CPT构造一个完全ADD，然后应用一定的规则去掉冗余节点，直到变为最简形式．借用Meinel和Thorsten[5]对OBDD冗余节点的定义，下面定理成立．

定理1如果ADD存在以下两种情况，则ADD存在冗余节点：

1)若存在某个节点，该节点的两个子节点(左孩子和右孩子)是一样的．表现在ADD中为，该点的实线边以及虚线边都指向同一个子节点，则该节点是重复的，称为第一类冗余节点；

2)若ADD中存在两个节点，该两个节点均代表变量X，且左孩子均指向同一个节点，右孩子均指向同一个节点，则这两个节点中有一个是重复的，称为第二类冗余节点．

图2(b)中的完全ADD表面并不符合定理1中的两种冗余情况，然而，需要注意的是，该完全ADD中若干概率值是相等的，需要对相同概率值节点进行合并，见图3(a)．显然，图3(a)存在上述两种冗余情况．合并了ADD叶节点后，其结构与OBDD完全相同，因此OBDD通过删除冗余节点获得最简结构的方法完全适用于ADD，保证了CPT等价最简ADD构造方法的正确性．

现结合OBDD简化理论[5]，总结从完全ADD得到最简ADD的步骤如下：

步骤1指定构造ADD的变量顺序，并构造完全ADD；

步骤2在完全ADD的基础上，去掉概率值相同的叶节点，将被去掉的叶节点的父节点重新指向保留下的具有相同概率值的唯一叶节点；

步骤3根据定理1，自下而上分析是否存在冗余节点；

步骤4自下而上逐步去掉冗余节点，直到根节点结束．

由Meinel和Thorsten[5]可知，按照如下方法自下而上逐层去掉冗余节点可以保证得到最简ADD．对于ADD中同层节点，删去两类节点的方法如下：

首先，删去第一类冗余节点，将该节点的父节点直接指向该节点的子节点；其次，删去第二类冗余节点，即去掉两个重复节点中的任意一个，将被删去节点的父节点指向被保留的另一重复节点，被删去节点的指向其左右孩子的两条边一同删去．

依照以上化简规则，图3给出了图2(b)中完全ADD的化简步骤．结果与图2(c)完全一致，验证了算法的正确性．综上，算法CPT-ADD给出了从任意CPT到其最简ADD转化的伪代码．

图3:ADD的化简步骤示意图

算法CPT-ADD(CPT,π,n)第5行用以判断第i个和第j个叶节点所表示的概率参数是否相等；第12行var(v)的含义是节点v表示的节点变量；第15行判断节点v的左右孩子节点是否为一个；以上分析与算法设计均是基于二元变量而言的．对多元变量的贝叶斯网络，通常会将多元变量转化为等价二元变量进行处理[6]，因而将多态贝叶斯网络转化为等价二态网络后，其相应的条件概率分布也可按上述方法用ADD表示．

算法CPT ADD(CPT,π,n)输入：CPT:一个条件概率表n:CPT包含的变量数目π:CPT中n个变量的某种排序,π={X1,···,Xn}输出：最简ADD 1：依照顺序π，构造CPT对应的完全ADD 2:numOfleafNode=exp(n)

由上述构造步骤和伪代码可看出，本文提出的ADD构造方法并没有对CPT的参数取值进行限制，因此，该构造方法为二态贝叶斯网络一般情形下的代数决策树构造方法．但需强调的是，首先，如2.2节所述，若CPT本身不存在环境独立情况，ADD概率参数存储量与CPT相同，并不能有效改善CPT存储过多问题．其次，实际工程应用中存在了大量的确定性或部分确定性因果逻辑关系[7,8]，例如“与”、“或”、“表决”、“功能触发”等．由2.1节对独立情况的定义可知，确定性或部分确定性因果逻辑关系其存在了大量的“独立情况”，例如，对于“与”逻辑，如果已知有一个父节点存在故障，则其它父节点状态与子节点状态就无关．因而贝叶斯网络作为一种因果逻辑关系的表达，其若用ADD存储确定性或部分确定性逻辑的概率参数，相对于CPT存储法，ADD方式必能大量降低存储量．因此，本文ADD方法可对任意CPT进行等价表达，虽并不意味着可减少任意CPT的概率参数量，但仍在工程实践中具有重要的应用价值．

4.2 案例分析与验证

图4是某型飞机起落架故障树[8]及其等价的贝叶斯网络，该等价贝叶斯网络根据文献[9-11]提出的故障树到贝叶斯网络的映射方法得来．其中A3节点对应的条件概率分布如果用CPT表示，则需要用exp(7)个参数，见表1，而如果用ADD表示，则只需要2×7=14个参数，见图5．类似地，对于与门节点A4，CPT表示方法需用exp(3)个参数，而用ADD表示方法需用2×3=6个参数．

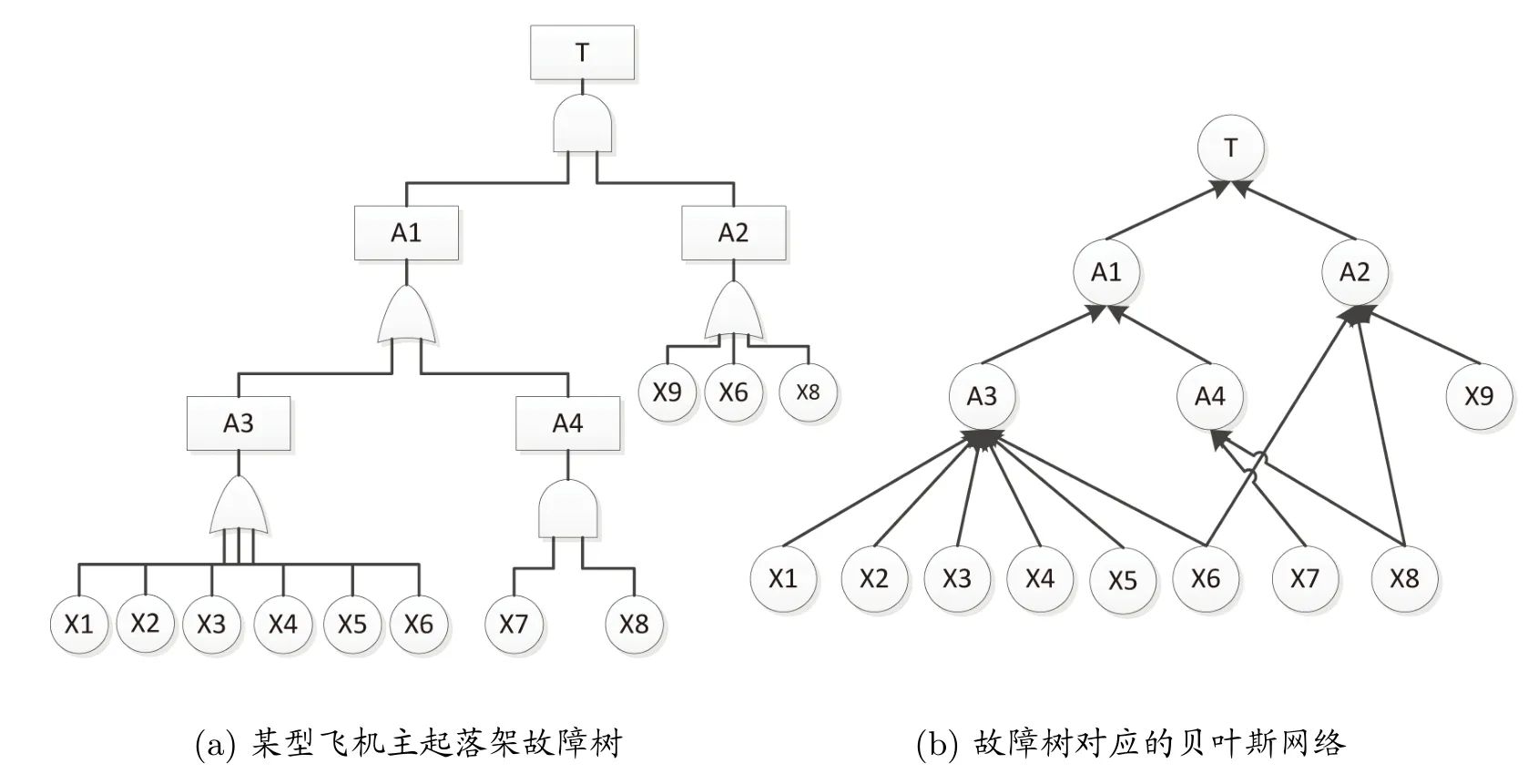
图4:某型飞机主起落架系统模型

表1: 节点A3的条件概率表

图5: 用ADD表示 P(A3|X1,X2,···,X6)

用ADD取代CPT不仅可以减少数据存储量，且可进一步降低运算量．现以求解系统可靠度为例来说明时间复杂度降低原理．对于由故障树转化来的贝叶斯网络，系统可靠性等价于在贝叶斯网络中求解概率Pr(T=0)[12-14]．现在采用经典变量消元算法求解该概率值，数学表达式如下

上述运算过程中，乘积P(A3|X1,X2,···,X6)P(X6)(节点A3与节点X6的条件概率分布的乘积)的计算最耗时．若用节点A3与节点X6对应的CPTs相乘，运算次数为exp(7)=128次；如果用两节点对应的ADDs相乘，计算次数为2×7=14次，文献[1,4]分别对CPTs与ADDs的运算法则进行了深入研究．

综上，利用ADD取代CPT来表示节点的CPD，可以大大提高由故障树转化而来的贝叶斯网络的推理效率，复杂度甚至可从指数级降到线性级：对于有n个基本事件的与/或门，采用CPT的存储方式，其时间和空间复杂度均为exp(n+1)；采用ADD存储方式，其时间和空间复杂度均为2(n+1)．对上述结论进一步推广：对于任何贝叶斯网络，如果其网络参数具有环境独立特点，应用ADD表示方式取代传统的CPT表示方式可减少概率参数的存储，从而进一步减少参与推理计算量，提高计算效率．

5 结论

本文通过对贝叶斯网络基本推理过程的研究，针对CPT不能捕捉网络参数环境独立的缺陷，提出了用ADD替代CPT来表示网络参数的方法，并给出了CPT到ADD的转化方法以及所需伪代码，保证了计算机编程实现的可行性．理论分析说明：利用ADD数据结构可减少网络参数存储量，降低网络推理复杂度，在贝叶斯网络推理算法研究方面具有重要意义．

参考文献：

[1]张连文，郭海鹏.贝叶斯网引论[M].北京：科学出版社，2006:30-53 Zhang L W,Guo H P.An Introduction to Bayesian Networks[M].Beijing:Science Press,2006:30-53

[2]史志富，张安.贝叶斯网络理论及其在军事系统中的应用[M].北京：国防工业出版社，2012:78-104 Shi Z F,Zhang A.Theory of Bayesian Network and its Application in Military System[M].Beijing:National Defense Industry Press,2012:78-104

[3]Boutilier C,Friedman N,Goldszmidt M,et al.Context-specific independence in Bayesian networks[C]//Proceedings of the Twelfth Annual Conference on Uncertainty in Artificial Intelligence(UAI-96),San Francisco:Morgan Kaufmann Publishers Inc.,1996:115-123

[4]Bahar R I,Frohm E A,Gaona C M,et al.Algebric decision diagrams and their applications[J].Formal Methods in System Design,1997,10(2-3):171-206

[5]Meinel C,Thorsten T.Algorithm and Data Structure in VLSI Design OBDD-Foundations and Applications[M].New York:Springer-Verlag,1988:89-103

[6]Darwiche A.Modeling and Reasoning with Bayesian Networks[M].New York:Cambridge University Press,2012:53-306

[7]Kim M C.Reliability block diagram with general gates and its application to system reliability analysis[J].Annals of Nuclear Energy,2011,38(11):2456-2461

[8]邓琼.安全系统工程[M].西安：西北工业大学出版社，2009:95-97 Deng Q.Safety System Engineering[M].Xi’an:Northwest Industrial University Press,2009:95-97

[9]杨昌昊，胡小建，竺长安.从故障树到故障贝叶斯网映射的故障诊断方法[J].仪器仪表学报，2009,30(7):1481-1486 Yang C H,Hu X J,Zhu C A.Fault diagnosis method mapping from fault trees to fault Bayesian networks[J].Chinese Journal of Scientific Instrument,2009,30(7):1481-1486

[10]Bobbio A,Portinale L,Minichino M,et al.Improving the analysis of dependable systems by mapping fault trees into Bayesian networks[J].Reliability Engineering&System Safety,2001,71(3):249-260

[11]王广彦，马志军，胡起伟.基于贝叶斯网络的故障树分析[J].系统工程理论与实践，2004,24(6):78-83 Wang G Y,Ma Z J,Hu Q W.The fault tree analysis based on Bayesian networks[J].Systems Engineeringtheory&Practice,2004,24(6):78-83

[12]周忠宝，董豆豆，周经伦.贝叶斯网络在可靠性分析中的应用[J].系统工程理论与实践，2006,26(6):95-100 Zhou Z B,Dong D D,Zhou J L.Application of Bayesian networks in reliability analysis[J].Systems Engineering-theory&Practice,2006,26(6):95-100

[13]Khakzad N,Khan F,Amyotte P.Safety analysis in process facilities:comparison of fault tree and Bayesian network approaches[J].Reliability Engineering&System Safety,2011,96(8):925-932

[14]Portinale L,Bobbio A.Bayesian networks for dependability analysis:an application to digital control reliability[C]//Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence,San Francisco:Morgan Kaufmann Publishers Inc.,1999:551-558