突发事件冲击下带通胀的动态资产配置问题研究∗

费为银,卢琴云,胡慧敏,夏登峰

(安徽工程大学数理学院，安徽芜湖 241000)

1 引言

投资组合选择问题一直以来都是金融数学研究领域中的一个最基本问题，资产配置是一种投资组合技术，利用资产配置可以有效的平衡投资风险．众所周知，现实生活中资本市场环境以及经济条件不总是一成不变的，投资者应该及时地对投资组合策略进行动态的调整．事实表明，突发事件的发生必然会引起资产价格的非连续变化，因此针对这种变化，研究突发事件冲击下的动态资产配置策略具有重要意义．

目前，已有大量文献用跳扩散过程来刻画突发事件冲击下资产价格的非连续变化现象．在投资组合问题研究中，Press[1]首次在纯扩散模型的基础上引入了跳跃行为．Merton[2]研究了风险资产可能违约的情形下短视资产的配置问题，违约事件是通过Poisson跳描述的并且使用随机控制方法获得最优资产配置策略．此后，国内外学者在此基础上，从不同角度研究了跳扩散环境下动态资产配置问题．近年来，费为银等[3-5]分别研究跳扩散环境下考虑通胀对资产配置的影响，模型不确定和极端事件冲击下带通胀的最优投资组合问题以及跳扩散环境下汇率变动的外商直接投资问题．梁勇等[6]研究了在跳扩散环境下红利支付对不确定厌恶投资者最优投资组合的影响．他们都是用股票价格服从跳扩散过程来刻画突发事件冲击，但是突发事件冲击下资产收益波动率也会发生跳跃行为．Bakshi等[7]进行了广泛的实证研究说明股票收益具有随机波动性和跳跃行为．Branger等[8]研究了股票收益波动率发生跳时的动态资产配置问题，说明对于跳风险也有一个对冲需求部分，波动率跳在投资组合计划中是一个非常重要的风险因子．因此，突发事件冲击下应该考虑资产收益波动率的跳跃行为．

另一方面，金融市场中通胀是投资者面临的最基本风险之一，自20世纪70年代以来，国内外许多学者研究了在通胀背景下的资产配置策略．Brennan和Xia[9]采用连续时间模型鞅方法研究了考虑通胀动态投资组合最优化问题，Munk等[10]探讨了投资于现金、名义债券和股票的投资者考虑通胀时最优资产配置，并利用美国的股票、债券和通胀数据去校验资本市场．近期，姚海洋等[11]研究了不确定时间和通货膨胀影响下风险资产的最优投资策略，费为银等[12]研究了通胀服从均值回复过程的最优消费和投资决策．梁勇等[13]研究了Knight不确定及机制转化环境下带通胀的最优消费投资问题研究．费为银和李淑娟[14]研究了Knight不确定下带通胀的最优消费和投资模型．上述文献中风险资产价格大多数是由Brown运动驱动，而实际生活中的风险资产价格有时会发生跳跃行为．

综上所述，突发事件发生时，考虑风险资产收益波动率的跳跃行为和通胀因素的模型更符合实际情况．本文在文献[15]中的事件风险模型基础上考虑了通货膨胀因素，并且通过数值模拟分析了风险资产收益波动率跳大小和通胀对投资组合策略的影响，对原有模型进行了进一步推广．本文安排如下：第2节给出模型的基本框架及相应的结论；第3节就所得的理论结果进行数值模拟分析，并给出经济学解释；在第4节对全文做了小结．

2 模型及结果

假设在金融市场中只有两种可投资的资产．一种是无风险债券，另一种是风险股票．设(Ω,F,{Ft},P)是一个完备的带流概率空间，在这个概率空间上的标准Brown运动和Poisson过程可以刻画经济状态的不确定性．设无风险债券价格S0服从dS0=rS0dt，风险股票价格St服从

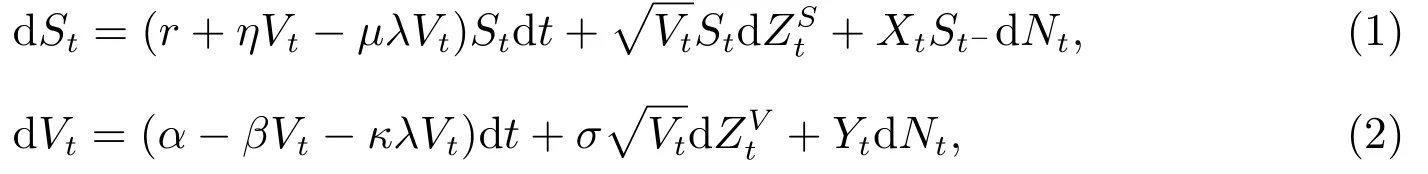
其中ZS和ZV是相关系数为ρ的标准Brown运动，N是随机到达强度为λV的Poisson过程，X(X∈(−1,∞))是均值为µ的价格跳大小，Y(Y∈[0,∞))是均值为κ的波动率跳大小，X和Y是独立的，且独立于ZS,ZV和N，θ=E[V]．

此外，金融市场中还存在一种通货膨胀风险．考虑通货膨胀折扣率It为带流概率空间(Ω,F,{Ft},P)上的可测适应过程，满足下面的随机微分方程

其中αI是t时刻预期通货膨胀率，σI是t时刻通胀波动率，ZI是标准Brown运动且和ZS的相关系数为ρ1，和ZV的相关系数为ρ2．

利用通货膨胀率对资产价格进行折算，折算后的价格分别为

根据伊藤-德布林公式推导出折算后的价格分别满足下面的随机微分方程

在Merton问题和文献[15]的基础上，本文主要研究考虑事件风险和通胀因素时最大化投资者终端财富的预期效用问题．投资者考虑幂型效用，在上述的两种资产上投资，并拥有初始财富W0，在每一个t(0≤t≤T)时刻投资者投资财富的ϕt比例在股票上，则与投资策略相关的财富过程Wt的动力学方程为

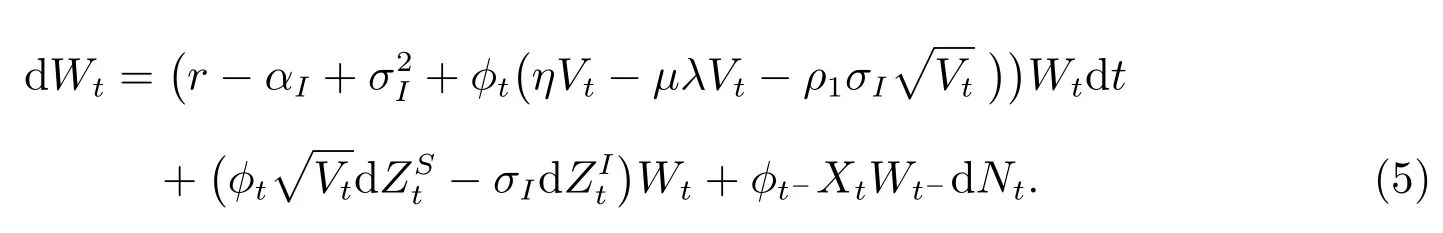
投资者的目标是

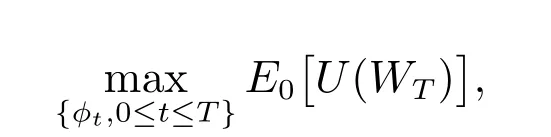
我们采用标准的随机控制方法来求解最优投资策略．类似Merton的思想，我们定义如下的间接效用函数

根据最优随机控制原理，我们可得到这个间接效用函数的HJB方程

其中JW,JV,JWW,JWV,JV V和Jt分别是J(W,V,t)关于W,V和t的偏导数．

为了保证最优投资策略存在，下面给出两个适度的正则条件

接下来的命题将给出最优动态资产配置策略．

命题1假设满足上述的两个正则条件，则动态资产配置问题有最优解

其中时变系数B(t)满足下面的常微分方程

且终端条件B(T)=0．

证明 首先对方程(7)关于ϕ求偏导得一阶条件

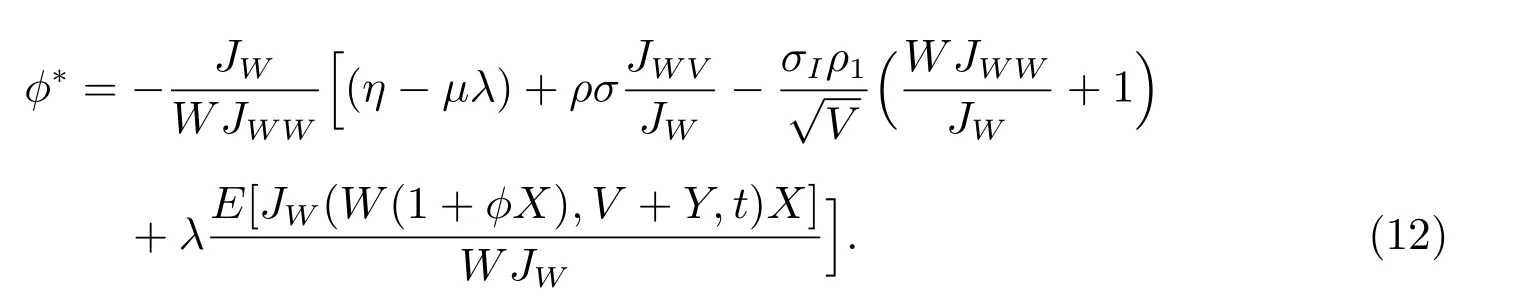
假设间接效用函数如下

求其各阶偏导得

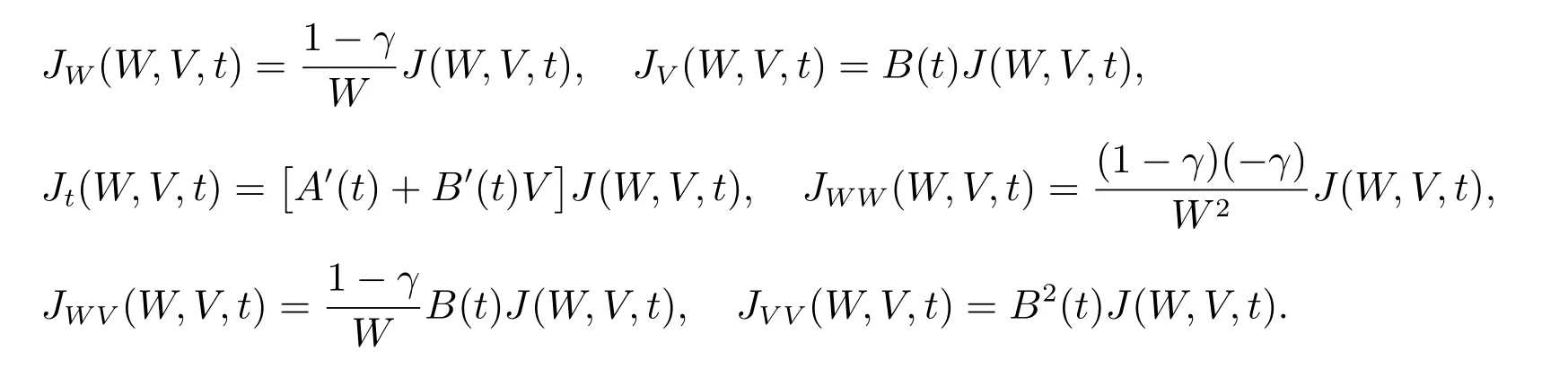
将上述各阶偏导数带入方程(12)式得

故有(10)式成立．接下来推导关于时变系数B(t)的常微分方程，我们将(13)和(14)式代入方程(7)得

上式对所有的V恒成立，则有(11)式成立．

3 数值模拟和经济意义分析

为了更直观地说明通胀因素和跳对投资者的动态资产配置策略的影响，下面分析收益波动率是随机的而跳大小是确定的这种简单情况下通胀因素和跳对投资者的动态资产配置策略的影响．

在这种情况下，模型的动力学方程为

根据命题1可知，上述情况下的最优动态资产配置策略为

且时变系数B(t)满足下面的常微方程

和终端条件B(T)=0.

由图1可见，当ρ=0.5时，即股票市场的不确定性和通胀的不确定性相关系数为正，随着通胀波动率的增大，股票价格波动变大，金融市场不稳定性增强，风险喜好的投资者(γ＞1)愿意承受高的风险以获得高的收益，从而在股票上的投资增加．当ρ=−0.5时，即股票市场的不确定性和通胀的不确定性相关系数为负，随着通胀波动率的增大，股票价格波动变小，金融市场相对稳定，风险喜好的投资者认为没有太高的收益可获得，反而减少了在股票上的投资．由此可知，当股票市场的不确定性和通胀的不确定性相关系数为正时，即通胀波动率增大，股票价格波动变大，金融市场不稳定性增强，风险厌恶的投资者(0＜γ＜1)担忧情绪上升，从而相应的减少风险股票的头寸．当股票市场的不确定性和通胀的不确定性相关系数为负，即通胀波动率增大，股票价格波动变小，金融市场相对稳定，风险厌恶的投资者担忧情绪有所缓和，从而相应的增加风险股票的头寸．

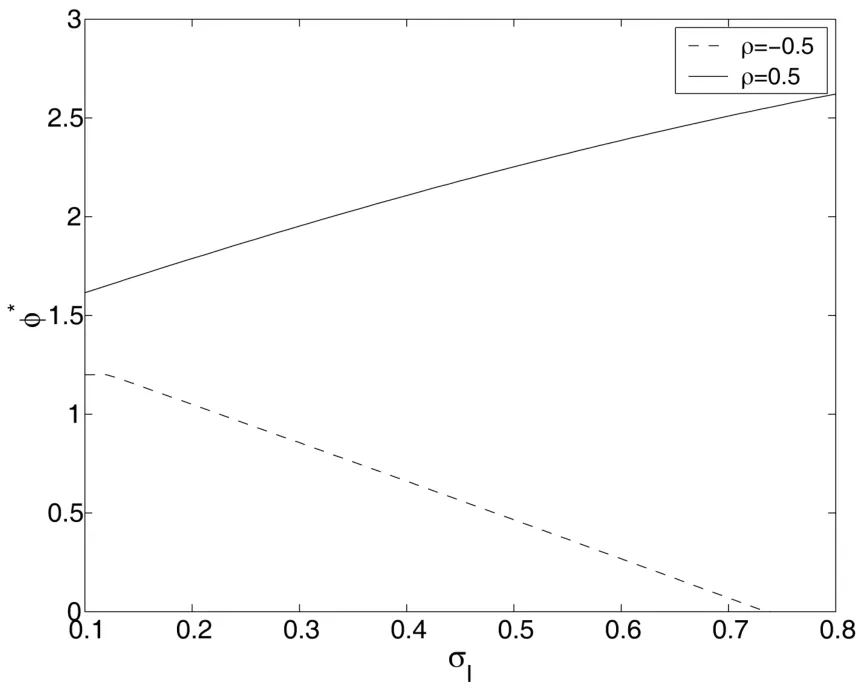
图1: 通胀波动率σI对资产配置策略ϕ∗的影响

由图2可见，对于特定的µ值，股票收益波动率跳大小越大，风险喜好的投资者会持有更多的股票，并且随着通胀波动率的增大，风险喜好的投资者对收益波动率跳大小变化的敏感度缓慢下降，当通胀波动率大于0.6时，经济环境恶化，投资者将避开投资大量不可预料的资产，风险喜好的投资者对收益波动率跳大小的变化几乎不敏感，收益波动率跳是否发生都不会改变投资者的股票头寸，投资者在股票上的配置很少甚至不配置，从而降低因高的通胀波动率所带来的经济损失．

图2: 通胀波动率σI和收益波动率跳大小κ对资产配置策略ϕ∗的影响

由图3可知，无论价格跳的方向如何，当股票价格发生跳时，投资者都将会相应地减少风险资产的配置，并且在低通胀波动率(0.2附近)的环境下，投资者在股票价格发生向上跳时持有的风险资产明显比股票价格发生同等幅度向下跳时的风险资产多，当通胀波动率大于0.6时，无论股票价格跳的方向如何，投资者都将持有少量风险资产甚至不持有．这是因为在低通胀波动率的环境下，投资环境好，金融市场稳定，投资者信心和积极性强，投资者认为股票价格发生向上跳时比股票价格发生同等幅度向下跳时的预期收益高，从而在股票价格发生向上跳时持有的风险资产明显比股票价格发生同等幅度向下跳时的风险资产多．当通胀波动率大于0.6时，这时的投资环境恶化，金融市场剧烈震荡，投资者担忧情绪上升，不再大量持有不可预料的风险资产，对股票价格跳也不再那么敏感，从而无论股票价格跳的方向如何，投资者都将持有少量风险资产甚至不持有风险资产．

图3: 通胀波动率σI和股票价格跳大小µ对资产配置策略ϕ∗的影响

4 小结

本文主要探讨了在突发事件冲击下，通货膨胀因素对动态资产配置策略的影响．当突发事件发生时，不管资产价格跳的方向和大小是如何变化，投资者都会减少风险资产的配置，然而对于特定的资产价格跳大小，风险喜好者将会随着收益波动率跳大小增加而增加风险资产配置．同时当通胀波动率过高时，经济恶化，金融市场波动剧烈，投资者对收益波动率跳大小和股票价格跳大小的变化都不再那么敏感，投资者将持有非常少的风险资产甚至不配置风险资产．总之，突发事件和通货膨胀对不同投资者的投资策略都有着重要的影响．因此，投资者应时刻关注国家宏观政策变化，根据不同的通胀程度和自己的风险承受能力，适时地调整自己的资产配置比例，以获得自己期望的收益．本文利用随机微分方程和随机控制理论，得到最优动态资产配置策略，并通过对简化模型的数值分析说明突发事件冲击下跳和通胀对投资者投资决策的影响．研究结果不仅可以扩展现有的模型，还可以为投资者提供一定的指导．

参考文献：

[1]Press S J.A compound events model for security prices[J].Journal of Business,1967,40(3):317-335

[2]Merton R C.Lifetime portfolio selection under uncertainty:the continuous time case[J].The Review of Economics and Statistics,1969,51(3):247-257

[3]费为银，蔡振球，夏登峰.跳扩散环境下带通胀的最优动态资产配置[J].管理科学学报，2015,18(8):83-94 Fei W Y,Cai Z Q,Xia D F.Dynamic asset allocation with inflation under jump-diffusion environment[J].Journal of Management Sciences in China,2015,18(8):83-94

[4]费为银，夏登峰，刘鹏.模型不确定和极端事件冲击下带通胀的最优投资组合选择问题研究[J].应用概率统计，2014,30(3):322-336 Fei W Y,Xia D F,Liu P.An investor’s optimal portfolio with rare events and model uncertainty under inflation[J].Chinese Journal of Applied Probability and Statistics,2014,30(3):322-336

[5]费为银，何丹丹，张伟.跳扩散下汇率变动的外商直接投资问题研究[J].系统工程理论与实践，2015,35(2):283-290 Fei W Y,He D D,Zhang W.Study of a foreign investor’s investment with fluctuations of exchange rate under jump-diffusion[J].System Engineering-Theory&Practice,2015,35(2):283-290

[6]梁勇，费为银，方和远，等.跳扩散环境下红利支付对不确定厌恶投资者最优投资组合的影响[J].东华大学学报，2015,41(2):273-276 Liang Y,Fei W Y,Fang H Y,et al.Impacts of the dividend payment on the optimal portfolio choice of an investor with the ambiguity aversion under jump-diffusion[J].Journal of Donghua University,2015,41(2):273-276

[7]Bakshi G,Cao C,Chen Z.Empirical performance of alternative option pricing models[J].Journal of Finance,1997,52(5):2003-2049

[8]Branger N,Schlag C,Schneider E.Optimal portfolios when volatility can jump[R].Working Paper,Vanderbilt University,2005

[9]Brennan M J,Xia Y.Dynamic asset allocation under inflation[J].The Journal of Finance,2002,57(3):1201-1238

[10]Munk C,Sørensen C,Nygaard V T.Dynamic asset allocation under mean-reverting returns,stochastic interest rates,and inflation uncertainty:are popular recommendations consistent with rational behavior?[J].International Review of Economics and Finance,2004,13(2):141-166

[11]姚海祥，伍慧玲，曾燕.不确定终止时间和通货膨胀影响下风险资产的最优投资策略[J].系统工程理论与实践，2014,34(5):283-290 Yao H X,Wu H L,Zeng Y.Optimal investment strategy for risky assets under uncertain time-horizon and inflation[J].System Engineering-Theory&Practice,2014,34(5):283-290

[12]费为银，吕会影，余敏秀.通胀服从均值回复过程的最优消费和投资决策[J].系统工程学报，2014,29(6):791-798 Fei W Y,Lv H Y,Yu M X.Decision making for optimal consumption and portfolio under inflation with mean-reverting process[J].Journal of Systems Engineering,2014,29(6):791-798

[13]梁勇，费为银，唐仕冰，等.Knight不确定及机制转换环境下带通胀的最优投资问题研究[J].数学杂志，2014,34(2):335-344 Liang Y,Fei W Y,Tang S B,et al.On study of optimal investment with inflation under Knightian uncertainty and regime-switching[J].Journal of Mathematics,2014,34(2):335-344

[14]费为银，李淑娟.Knight不确定下带通胀的最优消费和投资模型研究[J].工程数学学报，2012,29(6):799-806 Fei W Y,Li S J.Study on optimal consumption and portfolio with inflation under Knightian uncertainty[J].Chinese Journal of Engineering Mathematics,2012,29(6):799-806

[15]Liu J,LongstaffF,Pan J.Dynamic asset allocation with event risk[J].Journal of Finance,2003,58(1):231-259